Les phénomènes où apparaît le hasard peuvent être étudiés grâce aux probabilités. Mesurer des phénomènes aléatoires dont les valeurs peuvent prendre un nombre infini de valeurs différentes comme par exemple la durée de vie d'un appareil nécessite de travailler avec des lois dites continues.
Ce type de lois est aussi utiliser pour estimer une fiabilité.

Découverte des variables aléatoires continues

On désire mesurer la durée de vie en années d'un réfrigérateur à l'aide d'une variable aléatoire $X$. On suppose qu'un réfrigérateur peut fonctionner 100 ans au maximum.
Ainsi, $X$ peut prendre a priori toutes les valeurs dans l'intervalle $[0;100]$.

  1. Quelle est la probabilité que le durée du réfrigérateur soit exactement de 6.15680243 ans ?

  2. Quelle est la probabilité que le durée du réfrigérateur soit exactement de 74.458921 ans ?

  3. Plus généralement, soit $t$ un nombre réel quelconque de l'intervalle $[0;100]$.
    Quelle est la probabilité que le durée du réfrigérateur soit exactement de $t$ ans ?

Cependant, même si $P(X=6.15680243)=0$ et $P(X=74.458921)=0$, il semble plus probable que le réfrigérateur dure environ 6 ans qu'environ 74 ans : on dit qu'il y a une "densité de probabilité" plus élevée autour de 6 que de 74.
Ainsi, plutôt que de s'intéresser à une durée précise, on s'intéresse à la probabilité d'une durée de vie appartenant à un intervalle.

Loi uniforme

Exemple de découverte

Le tirage d'un nombre réel aléatoire $x$ dans $[0;10[$ paraît difficile à simuler car par exemple l'insctrution 10*ALEA() d'un tableur ne donne qu'un nombre au hasard dans $[0;10[$ n'ayant que 14 décimales.
Le but est de calculer la probabilité qu'un singe tapant au hasard sur le clavier d'un ordinateur donne l'écriture décimale de $\pi$ sachant que le premier nombre tapé donne le chiffre des entiers et que les autres donnent la succession de décimales.

  1. Quelle est la probabilité que le chiffre des unités soit le bon ?

  2. Quelle est la probabilité que les deux premiers chiffres soient les bons ?

  3. Quelle est la probabilité que les $n$ premiers chiffres soient les bons ?

  4. Il a été démontré par le mathématicien Lambert à la fin du XVIII ème siècle que le nombre $\pi$ avait une infinité de chiffres dans son écriture décimale.
    Quelle est la probabilité que le singe arrive à taper au hasard l'écriture décimale du nombre $\pi$ ?

On ne peut pas définir la variable aléatoire $X$ donnant le résultat $x$ du tirage d'un nombre réel dans $[0;10[$ en donnant une valeur à $P(X=x)$ car celle-ci est forcément nulle.
Ainsi, au lieu de définir la probabilité d'un réel, il est nécessaire de définir la probabilité d'un intervalle.

L'histogramme ci-dessous représente la fréquence $f_k$ des dix événements "$x\in [k;k+1[$"" pour 10000 réalisations de l'instruction =10*ALEA().
Le tableur affiche la courbe noire, appelée "courbe de tendance", qui "lisse" l'histogramme.

  1. Faire dessiner un histogramme pour une nouvelle série 10000 nombres aléatoires dans l'intervalle $[0;10[$ en cliquant sur l'icône .
    Que remarquez-vous ?

  2. Quelle est la fonction $f$ représentée par la "courbe de tendance" en noire ?

  3. Quelle est la probabilité $P(x\in[3;4[)$ ?

  4. Quelle est alors la probabilité $P(x\in[2;7[)$ ?

  5. Quelle probabilité est-il naturel d'associer à $P(x\in0[k;k+1[)$, avec $k$ compris entre 0 et 9, d'après la loi des grands nombres ?

  6. Conjecturer la valeur de la probabilité $P(x\in[\alpha;\beta[)$ où $\alpha$ et $\beta$ sont deux nombres dans $[0;10[$ tels que $\alpha \lt \beta$.

  7. Conjecturer la probabilité de $P(x\lt t)$ c'est-à-dire de $P(x\in[0;t[)$ où $t$ est un réel de $[0;10[$.

Définitions et propriétés

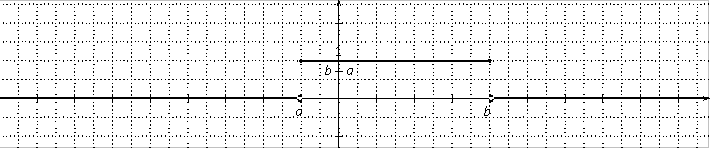
La loi continue uniforme $P$ sur $[a;b]$ modélise le choix d'un nombre réel au hasard dans l'intervalle $[a;b]$.
La loi uniforme est de densité définie sur $\mathbb{R}$ par $f(x)= \left \{ \begin{array}{l} \dfrac{1}{b-a}\text{ si }x\in[a;b] \\ 0\text{ sinon }\\ \end{array} \right. $.

Une entreprise vient d'envoyer un mail à un client à 13h. Vu le contenu du message, il est certain que le client va répondre par mail et que ce mail peut arriver n'importe quand entre 14h et 17h.
On admet que la durée d'attente du mail renvoyé par le client est modélisée par la variable aléatoire $T$ qui suit la loi uniforme sur l'intervalle $[14;17]$.

Déterminer la fonction densité de probabilité de $T$.

Soit $X$ une variable aléatoire suivant la loi uniforme sur l'intervalle $[a;b]$.

Soient $c$ et $d$ dans $[a;b]$ tels que $c\le d$.
La probabilité que $X\in[c;d]$ est notée $P([c;d])$.
$P([c;d])$ est l'aire du rectangle de hauteur $\dfrac{1}{b-a}$ et de longueur $d-c$.

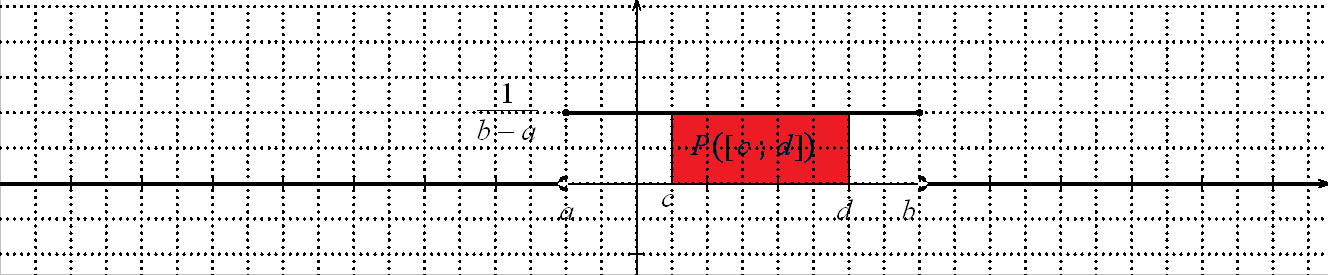
En effet : $\displaystyle P([c;d])=\int_c^d{\dfrac{1}{b-a} dt}=\dfrac{1}{b-a}\int_c^d{ dt}=\dfrac{1}{b-a} \left[t\right]_c^d$ $\displaystyle =\dfrac{1}{b-a} (d-c) = \dfrac{d-c}{b-a} $ $\displaystyle = \dfrac{\text{longeur de }[c;d]}{\text{longeur de }[a;b]}$

Comme la probabilité de tomber exactement sur un réel donné est nulle pour toute loi continue, $P({b})=P({c})=0$ donc :
$P(]b;c[)=P([b;c[)=P(]b;c])=P([b;c])=\dfrac{d-c}{b-a}$

Soit $X$ une variable aléatoire suivant la loi uniforme sur l'intervalle $[a;b]$. On a les propriétés suivantes sur les probabilités :

  1. $P([a;b])=1$.

  2. $P(\emptyset)=0$.

  3. Pour tout réel $x$ : $P({x})=0$.

  4. Si $a\le c\le d\le e\le f\le b$, alors $P([c;d]\cup [e;f])=P([c;d])+P([e;f])$.

On choisit au hasard un réel entre 0 et 1.

  1. Quelle est la probabilité que ce réel soit entre 0.4 et 0.6 ?

  2. Quelle est la probabilité que ce réel soit entre 0.1 et 0.8 sachant qu'il est supérieur à 0.5 ?

L'espérance mathématique d'une variable aléatoire $X$ suivant la loi uniforme sur l'intervalle $[a;b]$ est définie par : $\displaystyle E(X)=\int_a^b{t\times \dfrac{1}{b-a} dt}$.

  1. L'espérance mathématique d'une variable aléatoire $X$ suivant la loi uniforme sur l'intervalle $[a;b]$ correspond à la moyenne de tous les nombres entre $a$ et $b$.

  2. $E(X)=\dfrac{a+b}{2}$.

  1. La variance d'une variable aléatoire $X$ suivant la loi uniforme sur l'intervalle $[a;b]$ est définie par $\displaystyle V(X)=\int_a^b{(t-E(X))^2\times \dfrac{1}{b-a} dt}$.

  2. Son écart-type est définie par $\sigma(X)=\sqrt{V(X)}$.

  1. La variance et l'écart-type mesurent la dispersion moyenne des valeurs de la variable aléatoire $X$ par rapport à la moyenne $E(X)$.

  2. $V(X)=\dfrac{(b-a)^2}{12}$.

  3. $\sigma(X)=\sqrt{V(X)}=\dfrac{b-a}{2\sqrt{3}}$.

  4. Lorsque $X$ correspond au choix aléatoire d'un nombre entre $a$ et $b$; $\sigma(X)$ correspond à l'écart moyen de tous les nombres entre $a$ et $b$ avec le centre du segment $[a;b]$.

À partir de 7h00, un bus passe toutes les quinze minutes à l'arrêt A.
Un usager se présente en A entre 7h et 7h30. On fait l'hypothèse que la durée $X$ (en minutes) entre 7h00 et l'heure de son arrivée en A est une variable aléatoire uniformément répartie sur l'intervalle $[0;30]$.

  1. Calculer la probabilité de l'événement $E$ « cet usager attend moins de 5 minutes ».

  2. Est-ce qu'il est vrai, suivant cette modélisation, qu'un bus passe en moyenne toutes les quinze minutes à l'arrêt A ?

Loi normale ou loi de Laplace-Gauss

Introduction

Voici ci-dessous la représentation graphique de la loi binomiale $\mathcal{B}(130;0.3)$ :

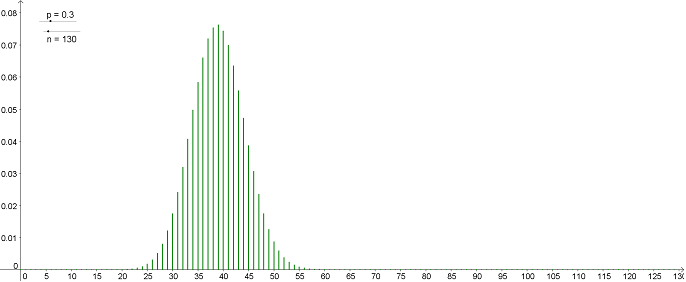
Au lieu de représenter par un diagramme bâtons, on utilise un histogramme centré et de hauteur donnée par chacun des bâtons.

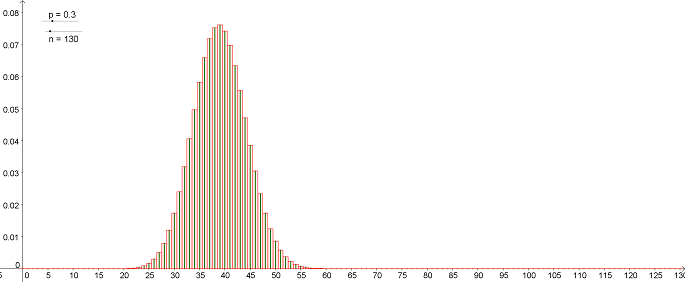
On chercher une courbe qui approche le contour de l'histogramme afin de remplacer la loi binomiale par une loi continue. Voici une courbe qui convient bien :

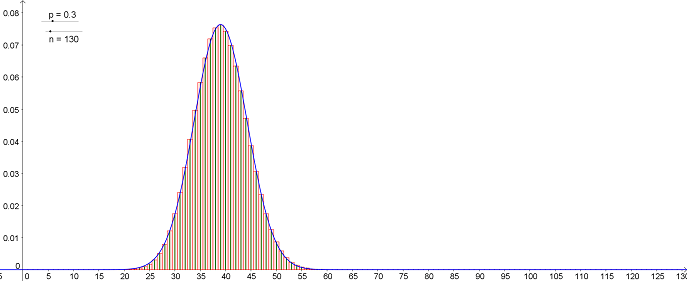
On admet que la courbe bleue représente la fonction $f$ définie sur $\mathbb{R}$ par : $\displaystyle f(x)= \dfrac{1}{\sigma \sqrt{2 \pi}} e^{-\dfrac{(x-m)^2}{2\sigma^2}}$ où $m$ représente l'espérance de la loi binomiale initiale et $\sigma$ son écart type.

Vous pouvez visualiser cette approche grâce à l'activité GeoGebra ci-dessous en cliquant sur les doubles chevrons en-dessous du graphique pour faire évoluer les étapes de l'approximation :

En modifiant les paramètres $p$ et de $n$ de la loi binomiale, vous pouvez vérifier que cette approximation est correcte dès que $n$ est "suffisamment grand".

Définition

Une variable aléatoire continue $X$ à valeurs dans $\mathbb{R}$ suit une loi normale de paramètres $m$ et $\sigma$ si sa densité de probabilité est la fonction $f$ définie sur $\mathbb{R}$ par : $\displaystyle f(x)= \dfrac{1}{\sigma \sqrt{2 \pi}} e^{-\dfrac{(x-m)^2}{2\sigma^2}}$.
La loi de probabilité de la variable aléatoire réelle $X$ est notée $\mathcal{N}(m,\sigma)$.

Si $X$ suit la loi normale $N(m,\sigma)$ alors : $E(X)=m$, $V(X)=\sigma^2$ et $\sigma(X)=\sigma$.

"$\mathcal{N}(m;\sigma)$" se lit "loi normale d'espérance $m$ et d'écart type $\sigma$".

La moyenne $m$ est souvent notée $\mu$.
Dans GeoGebra, c'est avec cette lettre grecque qu'apparaîtra la valeur de ce paramètre correspondant à la moyenne.

Pour vous habituer à cela, dans la suite du cours, nous utiliserons soit $m$, soit $\mu$ pour ce paramètre.

Courbe représentative de la densité

Voici les représentations de la densité $f$ d'une loi normale pour différents couples de paramètres $(m,\sigma)$.

  1. Associer à chaque courbe le couple $(m,\sigma)$ parmi $(1;0.4)$, $(1;1)$ et $(1;3)$.

  2. Quelle est l'influence de $\sigma$ sur la courbe ?

Voici les représentations de la densité $f$ d'une loi normale pour différents couples de paramètres $(m,\sigma)$.

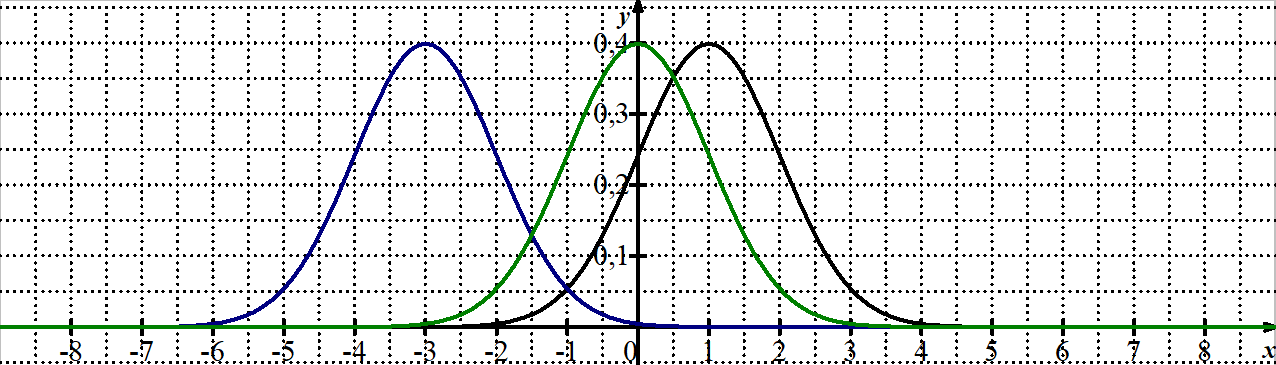
  1. Associer à chaque courbe le couple $(m,\sigma)$ parmi $(-3;0.2)$, $(0;0.2)$ et $(1;0.2)$.

  2. Quelle est l'influence de $m$ sur la courbe ?

La courbe représentant la fonction densité de $f$ une loi normale de paramètres $\mu$ et $\sigma$ :

  1. a l'allure d'une "cloche",

  2. est symétrique par rapport à la droite verticale d'équation $x=\mu$,

  3. est d'autant plus aplatie que l'écart type $\sigma$ est élevé.

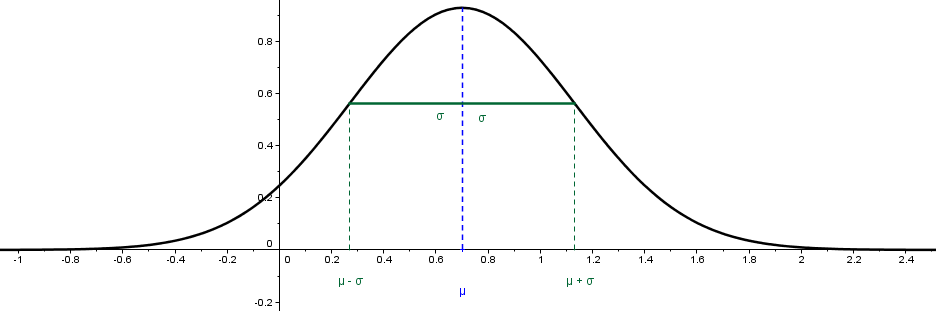
Soit $X$ une variable aléatoire suivantt la loi normale d'espérance $\mu$ et d'écart type $\sigma$.

En raisonnant sur la courbe, on peut visualiser les probabilités et déduire différentes propriétés de "symétrie" :

  1. On peut visualiser $\color{blue}{P(X \le t)}$ :

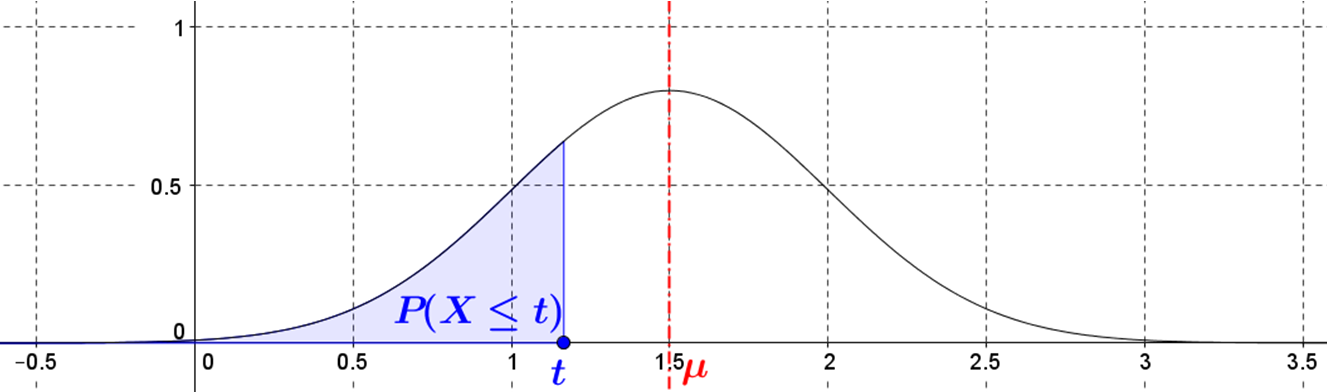
  2. $\color{Green}{P(X>t)}=1-\color{blue}{P(X \le t)}$ :

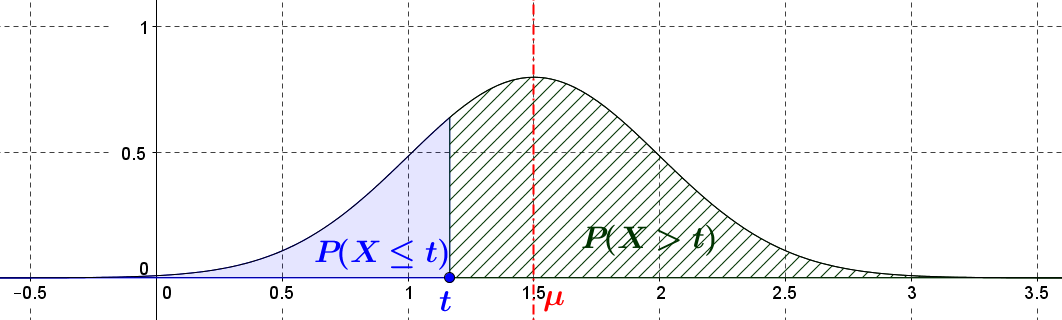
  3. On peut visualiser $\color{blue}{P(a \lt X \le b)}$ :

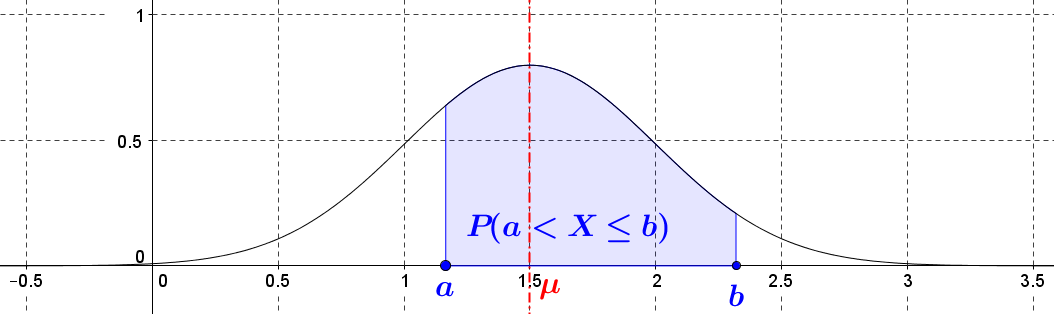
  4. $\color{blue}{P(\mu-a\lt X\lt \mu+a)}=2\color{red}{P(\mu \le X\lt \mu+a)}$ :

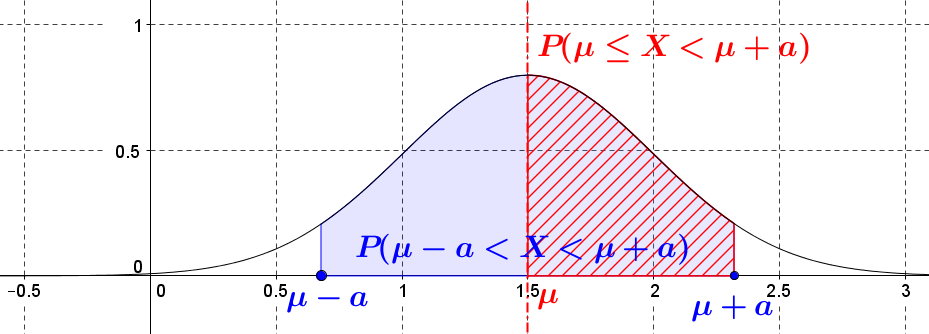
  5. $\color{blue}{P(\mu-a\lt X\lt \mu+a)}=1-2\color{red}{P(X\lt \mu-a)}$ :

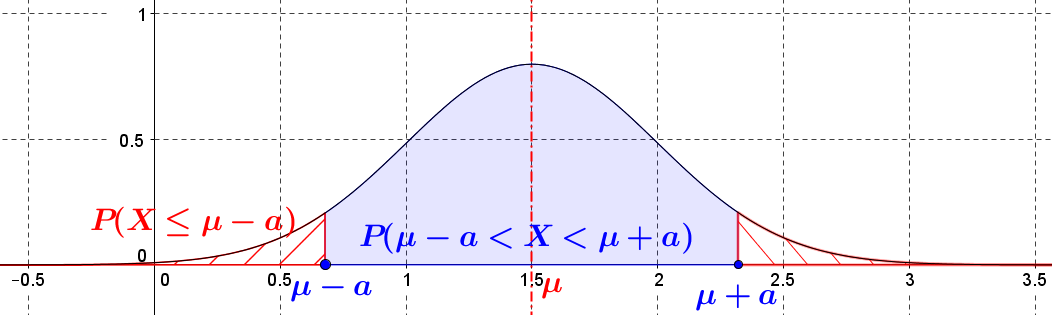
Calculs de probabilité sur GeoGebra

Pour obtenir une valeur approchée de $P(a \lt X \lt b)$ sur GeoGebra :
il suffit d'aller dans l'onglet Calculs de probabilités (comme pour la loi binomiale), puis :

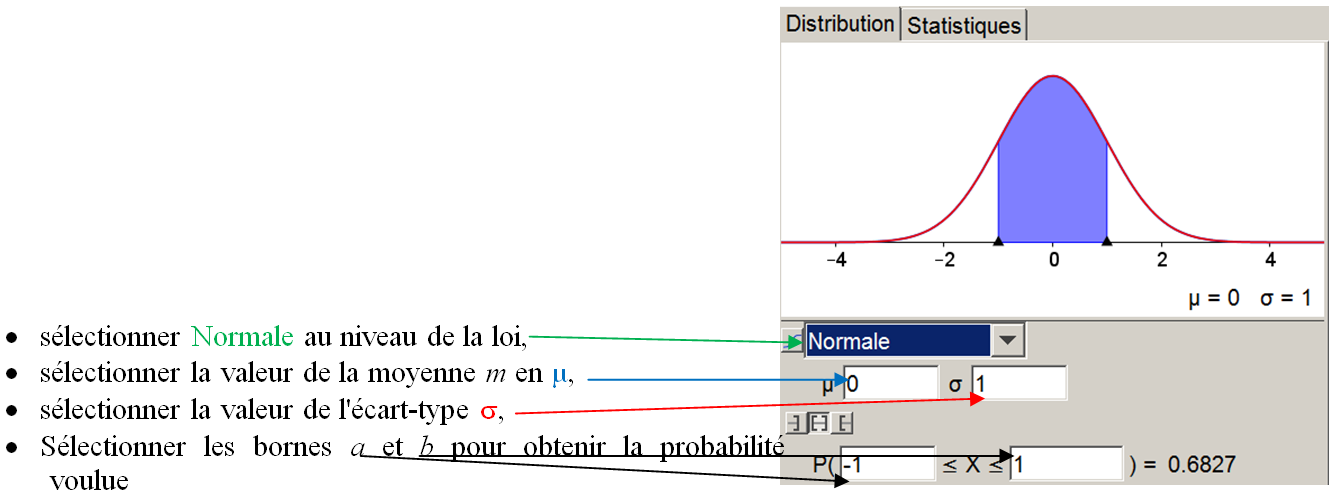
Pour trouver une valeur approchée du nombre réel $k$ tel que $P(X\lt k)=c$, avec $c\in[0;1]$ : deux méthodes :

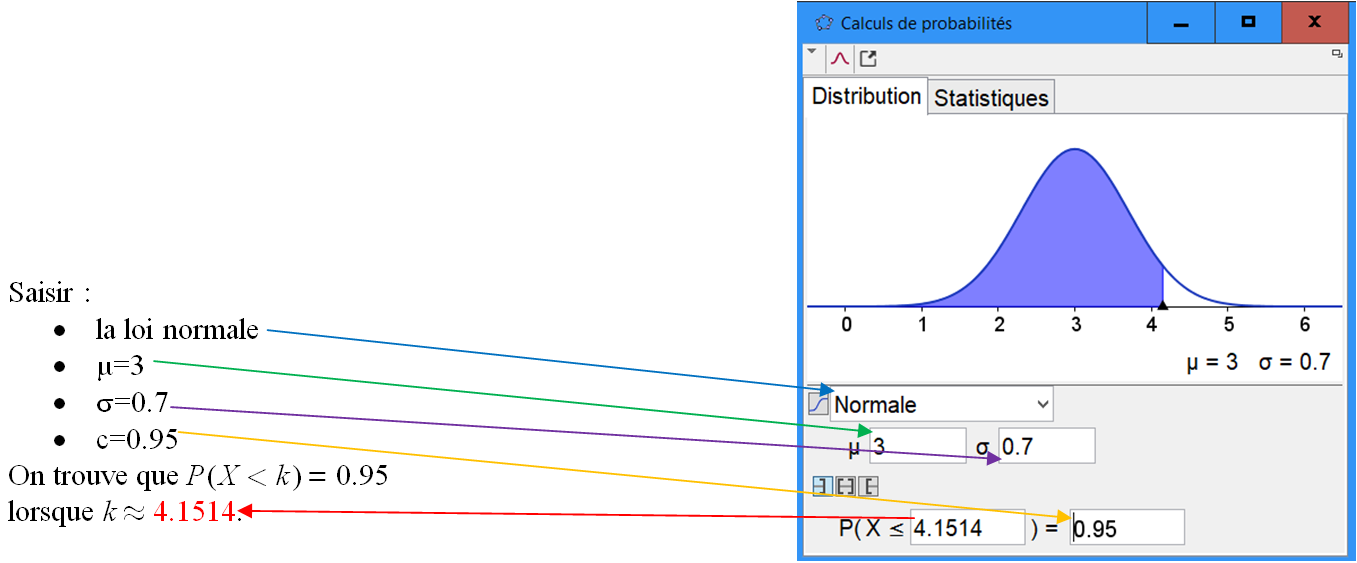
Trois probabilités remarquables :

  1. $P(\mu-\sigma \le X\le \mu+\sigma)\approx 0.683$.

  2. $P(\mu-2\sigma \le X\le \mu+2\sigma)\approx 0.954$.

  3. $P(\mu-3\sigma \le X\le \mu+3\sigma)\approx 0.997$.

Une usine produit des bobines de fil électrique. On désigne par $X$ la variable aléatoire qui, à toute bobine tirée au hasard de la production d'une journée associe la longueur, exprimée en mètres, du fil de cette bobine.
On admet que $X$ suit la loi normale de moyenne 50 et d'écart type 0.2.
On prélève au hasard une bobine dans la production d'une journée.

  1. Calculer la probabilité de chacun de l'événement $A$ : "La longueur du fil de la bobine est inférieure à 50.19 mètres".

  2. Calculer la probabilité de chacun des événements suivants :

    1. La longueur du fil de la bobine est supérieure à 50.16 mètres.

    2. La longueur du fil de la bobine est comprise entre 50.16 et 50.19 mètres.

  3. Déterminer le nombre réel positif $a$ tel que $P(50-a \le X \le 50+a)=0.9$.

Une machine fabrique des tubes métalliques de diamètre attendu 12mm.
Cependant, le diamètre réel $X$ (en mm) fluctue légèrement de manière aléatoire autour de cette valeur : il suit la loi normale d'espérance 12 et d'écart-type 0.08.
Les tubes de diamètre inférieur à 11.9 ou supérieur à 12.2 sont rejetés.

  1. Donner une valeur approchée de $P(X\lt 11.9)$ à $10^{-3}$ près.

  2. Déterminer $P(X\gt 12.2)$ à $10^{-3}$ près.

  3. Calculer la probabilité qu'un tube métallique pris au hasard soit rejeté lors du test de mesure du diamètre ?

Loi normale centrée réduite

On dit qu'une variable aléatoire $T$ suit la loi normale centrée réduite, notée $\mathcal{N}(0;1)$ signifie que sa densité de probabilité est la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=\dfrac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}$.

Voici la représentation graphique de $f$, la densité de la loi normale centrée réduite :

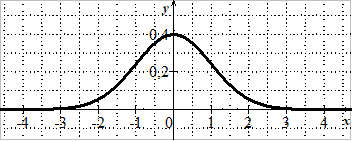
Approximation d'une loi binomiale par une loi normale

On a vu qu'une loi binomiale peut être approchée par une loi normale.
Ce faisant, les deux lois doivent avoir la même moyenne et le même écart type. Ainsi :

Lorsque $n$ est grand et $p$ ni trop près de 0, ni trop près de 1 alors la loi binomiale $\mathcal{B}(n;p)$ est très proche de la loi normale $\mathcal{N}(m,\sigma)$ avec $m=np$ et $\sigma=\sqrt{npq}=\sqrt{np(1-p)}$.

Attention, pour appliquer ce théorème, on utilise la correction de continuité !

Soit $X$ une loi binomiale approchée par une loi normale notée $Y$.

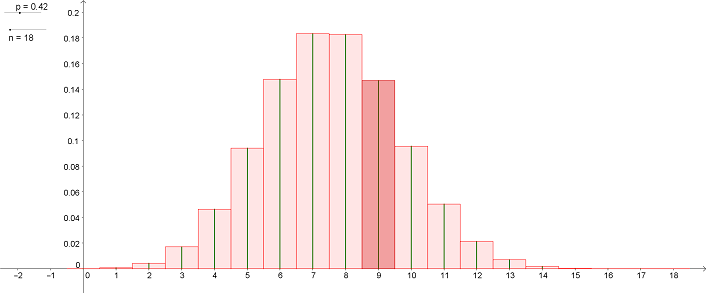
Comme on remplace chaque bâton représentant la loi binomiale par un rectangle centré sur ce bâton, au lieu de calculer la hauteur $P(X=k)$ du bâton, on calcule l'aire du rectangle donc $P(k-0.5\le X\le k+0.5)$.

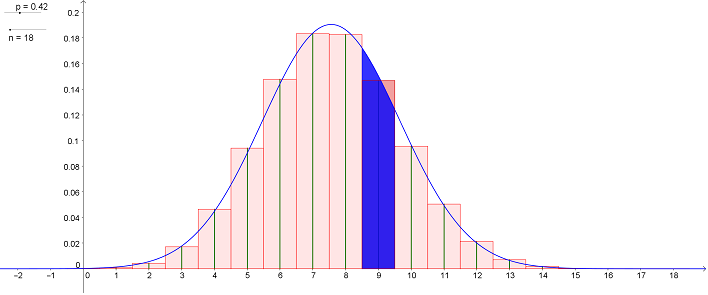
Ainsi, en utilisant la loi normale $Y$ au lieu de la loi binomiale $X$, on a : $P(X=k)\approx P(k-0.5\le Y \le k+0.5)$.

Pour corriger le fait de remplacer une loi discrète par une loi continue, il faut faire une correction de continuité en remplaçant une valeur $k$ de la loi discrète par l'intervalle $[k-0.5;k+0.5]$ de la loi continue.
Ainsi, on effectue les substitutions suivantes :

$X$ suit une loi binomiale

$Y$ suit une loi binomiale

$P(X=k)$ $P(k-0.5\le Y \le k+0.5)$
$P(X\le k)$ $P(Y \le k+0.5)$
$P(X\ge k)$ $P(Y \ge k-0.5)$
$P(a\le X \le b)$ $P(a-0.5\le Y \le b+0.5)$

Dans cette activité, chaque probabilité demandée sera arrondie à $10^{-3}$.
Une enquête réalisée par un institut de sondage permet d'estimer que la probabilité qu'une lettre, choisie au hasard dans le courrier d'une entreprise, parvienne à son destinataire en France le lendemain est 0.7.
Dans une des agences d'une grande entreprise, on admet que l'on expédie 500 lettres par jours.
On note $X$ la variable aléatoire qui, à un jour tiré au hasard, associe le nombre de lettres qui parviendront à leur destinataire le lendemain.
On suppose que les acheminements de ces lettres se font en toute indépendance.

    1. Expliquer pourquoi $X$ suit une loi binomiale et préciser les paramètres de cette loi.

    2. Calculer l'espérance mathématique de $X$, puis la valeur arrondie à $10^{-2}$ de l'écart type de $X$.

    3. Calculer la probabilité que 355 lettres exactement, sur les 500 expédiées un jour tiré au hasard, parviennent à leur destinataire le lendemain.

  2. Soit $P_0$ la probabilité qu'au moins 375 des 500 lettres expédiées un jour tiré au hasard, parviennent à leur destinataire le lendemain. Calculer la probabilité $P_0$.

  3. Pour calculer une valeur approchée $P'_0$ de $P_0$, on pense approcher la loi de $X$ par la loi de $Y$, où $Y$ est une variable aléatoire suivant la loi normale $\mathcal{N}(350;10.25)$.

    1. Justifier que les deux paramètre choisis sont pertinents.

    2. Déterminer $P'_0$ à $10^{-2}$ près par défaut en appliquant la correction de continuité puis estimer $P_0$.

  4. Estimer la probabilité que le nombre de lettres, sur les 500 expédiées un jour choisi au hasard, parvenant à leur destinataire, le lendemain, soit compris entre 340 et 365.

Theorème central limit

$X$ et $Y$ sont deux variables aléatoires réelles.
On dit que $X$ et $Y$ sont indépendantes si, pour tous les réels $x$ et $y$, on a : $P(Y\le y\text{ et }X\le x)=P(Y\le y)\times P(X\le x)$.

Pour tout réel $a$ et $b$, on a :

  1. $E(aX+b)=aE(x)+b$.

  2. $V(aX+b)=a^2 V(x)$.

Pour toute variable aléatoire $X$ et $Y$, on a : $E(X+Y)=E(X)+E(Y)$ et $E(X-Y)=E(X)-E(Y)$.

Pour toute variable aléatoire $X$ et $Y$ indépendantes, on a : $V(X+Y)=V(X-Y)=V(X)+V(Y)$.

Théorème central limit

Soit $(X_n)$ une suite de variables aléatoires réelles indépendantes suivant la même loi de probabilité d'espérance $\mu$ et d'écart type $\sigma$.
Pour $n$ suffisamment grand ($n\le 30$), la variable aléatoire $\overline{X}=\dfrac{X_1+X_2+...+X_n}{n}$ suit approximativement la loi normale $\mathcal{N}\left(\mu;\dfrac{\sigma}{\sqrt{n}}\right)$.

Exercices

Loi uniforme

Le standard téléphonique d'un grand magasin limite la durée d'attente en transférant le plus vite possible les appels sur d'autres postes. On s'intéresse aux appels dont la durée d'attente est comprise entre 10 secondes et 1 minute.
On note $T$ la variable aléatoire qui, à un tel appel pris au hasard, associe la durée d'attente. On admet que $T$ suit la loi uniforme sur cet intervalle $[10;60]$.

  1. Donner la fonction de densité de $T$.

  3. Déterminer les probabilités suivantes :

    1. $P(A)$ où $A$ est l'événement "la durée d'attente est inférieure à 20 secondes".

    2. $P(B)$ où $B$ est l'événement "la durée d'attente est supérieure à 40 secondes".

    3. $P(C)$ où $C$ est l'événement "la durée d'attente est comprise entre 20 et 40 secondes".

  4. Déterminer l'espérance $E(T)$ puis donner une interprétation de $E(T)$.

  5. Déterminer la variance $V(T)$.

Un appareil de mesure évalue l'épaisseur en centimètres de pièces mécaniques. Cette épaisseur est modélisées par une variable aléatoire $X$ suivant la loi uniforme sur $[0;20]$.
Les pièces sont acceptées si leur épaisseur est supérieure à 12 cm.

  1. Déterminer la fonction de densité $f$ de $X$.

  2. Calculer la probabilité qu'une pièce soit acceptée.

  3. Une pièce a une épaisseur supérieure à 10 cm. Quelle est la probabilité qu'elle soit acceptée ?

    1. Calculer l'espérance $\mu=E(X)$ et l'écart type $\sigma=\sigma(X)$.

    2. Calculer la probabilité $P(\mu-\sigma\lt X \lt \mu+\sigma)$.

Antoine arrive à un arrêt de bus sans avoir consulté les horaires. Sur cette ligne, un bus part toutes les 8 minutes. On note $X$ la variable aléatoire donnant, en minutes, le temps d'attente d'Antoine jusqu'au départ du bus.

  1. Quelle est la loi suivie par $X$ ?

  2. Calculer la probabilité qu'Antoine attende :

    1. Au moins 5 minutes.

    2. Moins de 2 minutes.

    3. Entre 3 et 6 minutes.

    4. Exactement 7 minutes.

  3. Déterminer le temps moyen d'attente.

Loi normale

La variable aléatoire $X$ suit la loi normale $\mathcal{N}(24;6)$. Calculer :

  1. $P(X\le 30)$.

  2. $P(X\ge 30)$.

  3. $P(X\le 21)$.

  4. $P(27\le X\le 33)$.

  5. $P(18\le X\le 20)$.

Sachant que la variable aléatoire $X$ suit la loi normale $\mathcal{N}(24;6.5)$, déterminer à $10^{-2}$ près $a$ tel que :

  1. $P(X\le a)=0.95$.

  2. $P(24-a\le X\le 24+a)=0.99$.

Sachant que la variable aléatoire $X$ suit la loi normale $\mathcal{N}(0;1)$, déterminer à $10^{-3}$ près $a$ tel que :

  1. $P(X\le a)=0.99$.

  2. $P(-a\le X\le a)=0.95$.

L'entreprise agroalimentaire Flavornuts fabrique des arômes naturels servant à l'amélioration des préparations culinaires pour la pâtisserie ou la cuisine. Elle les conditionne dans des flacons de 58 ml qu'elle achète à l'entreprise Verremballage, qui conçoit, développe et commercialise des solutions d'emballages primaires composées de flacons standards.
Les parties A et B peuvent être traitées de façon indépendante.

Partie A : Étiquetage

L'étiquetage des denrées alimentaires préemballées est obligatoire (articles R. 112-1 et suivants du code de la consommation). Certaines mentions sont imposées par la législation, d'autres sont facultatives. Toutes sont fournies par les fabricants, sous leur responsabilité. L'étiquetage est constitué par «les mentions, indications, marques de fabrique ou de commerce, images ou signes se rapportant à une denrée alimentaire et figurant sur tout emballage, document, écriteau, étiquette, bague ou collerette accompagnant ou se référant à cette denrée alimentaire (article R. 112-1 du code de la consommation). » Une fois fabriquées, les étiquettes peuvent présenter deux défauts : un défaut du visuel (graphisme, photo, couleur, ...) ou l'absence de la date limite de consommation. On considère les évènements suivants :

On suppose que les évènements $A$ et $D$ sont indépendants.
On admet que les probabilités des évènements sont : $P(A)=0,01$ et $P(D)=0,03$.

  1. Calculer la probabilité qu'une étiquette prélevée au hasard dans la production présente les deux défauts.

  2. Calculer la probabilité qu'une étiquette prélevée au hasard dans la production ne présente aucun de ces deux défauts.

Partie B : Étude de la contenance

Dans cette partie, les résultats seront arrondis, si nécessaire, à $10^{-2}$ près.
On définit une variable aléatoire $V$ associant à chaque flacon son volume utile exprimé en mL.
On suppose que $V$ suit la loi normale de moyenne $\mu=58$ (valeur annoncée par le fournisseur) et d'écart type $\sigma=0,04$.
Le cahier des charges indique que le flacon est conforme lorsque ce volume appartient à l'intervalle $[57,90;58,10]$.
On choisit un flacon au hasard dans la production.

  1. Déterminer la probabilité pour qu'il soit non conforme.

  2. Donner une valeur arrondie au centième du réel $h$ tel que : $P(58-h \le V\le 58+h)=0,95$.

Une entreprise produit en grande série des axes de rotation pour un modèle de moteur.
L'entreprise met en place un contrôle de qualité portant sur le diamètre des axes de rotation fabriqués.
On appelle $L_{C1}$ et $L_{C2}$ les limites de contrôle. On admet que $L_{C1}=14,4$ mm et $L_{C2}=15,9$ mm.
On note $D$ la variable aléatoire qui, à tout axe de rotation prélevé au hasard dans la production totale des vingt machines pendant un cycle de fabrication, associe son diamètre exprimé en millimètres. On admet que $D$ suit une loi normale de moyenne $\mu=15.20$ et d'écart-type $\sigma=0.3$.

  1. Déterminer à $10^{-4}$ près la probabilité que le diamètre d'un axe pris au hasard dans la production soit compris entre les limites de contrôle.

  2. Déterminer un intervalle $[L_{S1};L_{S2}]$, centré en $\mu=15,20$ et tel que la probabilité que la variable $D$ prenne une valeur entre $L_{S1}$ et $L_{S2}$ soit environ égale à 0,95.
    Les nombres $L_{S1}$ et $L_{S2}$ s'appellent les limites de surveillance.

Une usine produit des bobines électriques.
1.3% des bobines produites sont défectueuses.

Une des chaînes de fabrication de l'usine doit répondre à une commande spécifique.
On modélise l'inductance, exprimée en henry (H) d'une bobine par une variable aléatoire $Y$.
On admet que $Y$ suit la loi normale de moyenne $\mu=1$ et d'écart type $\sigma=0,02$.
Quelle est la probabilité qu'une bobine prise au hasard dans la production ait une inductance comprise entre 0,96 H et 1,04 H ? Arrondir au centième.

Partie A. Défauts de fabrication

Un verre à pied est constitué de deux parties : le calice (ou bol) et le pied. Ces deux parties sont assemblées à chaud et fabriquées par deux procédés différents. Elles peuvent présenter des défauts indépendamment l'une de l'autre.

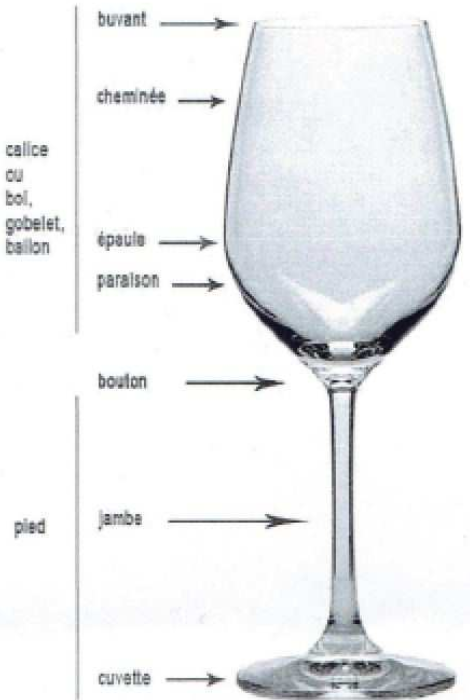
On a constaté que la machine qui fabrique les calices produit 5% de calices défectueux et que la machine qui fabrique les pieds produit 2% de pieds défectueux. On appelle $A$ l'évènement "le calice est défectueux" et $B$ l'évènement "le pied est défectueux".
On prélève un verre au hasard dans la production.

  1. Calculer la probabilité pour que le verre ait les deux défauts.

  2. Calculer la probabilité pour que le verre soit défectueux c'est-à-dire que le verre ait au moins un des deux défauts.

Partie B. Diamètre du buvant du verre

Dans cette question on s'intéresse au diamètre, exprimé en millimètre, d'ouverture du verre appelée "buvant" du verre.
On note $D$ la variable aléatoire qui à chaque verre associe le diamètre de son "buvant".
On admet que $D$ suit la loi normale de paramètres $\mu=46$ et $\sigma=0,3$. br On prélève au hasard un verre dans la production.

  1. Calculer à $10^{-2}$ près la probabilité que le diamètre de ce verre soit compris entre 45,8 et 46,3.

  2. Déterminer une valeur approchée à $10^{-1}$ près du nombre réel $a$ tel que $P(46-a \le D\le 46+a)=0.99$.

Loi binomiale et loi normale

On s'intéresse à l'ensemble des planches produites par l'entreprise dans une journée.

  1. On note $X$ la variable aléatoire qui, à toute planche prélevée au hasard dans cette production, associe sa longueur en cm. On admet que $X$ suit la loi normale de moyenne $\mu=80,2$ et d'écart type $\sigma=0,17$.
    Une planche est jugée conforme par l’entreprise si sa longueur en cm est dans l’intervalle $I=[79,9~;~80,5]$.

    1. Déterminer un nombre décimal $h$ tel que $P(80,2-h \le X\le 80,2+h)\approx 0,95$ (à $10^{-2}$ près).
      Interpréter ce résultat en termes de production de planches.

    2. On extrait au hasard une planche de la production. Calculer, à $10^{-3}$ près, la probabilité que la planche soit conforme.

  2. On suppose que la probabilité qu'une planche extraite au hasard de la production soit non conforme est égale à 0,08.
    L'aménagement d'espaces habitables nécessite 250 planches. L'entreprise prélève au hasard un lot de 250 planches dans la production, suffisamment grande pour que ce prélèvement puisse être assimilé à un prélèvement avec remise.
    On appelle $Y$ la variable aléatoire, qui à tout prélèvement de 250 planches, associe le nombre de planches non conformes.

    1. Quelle loi suit la variable aléatoire $Y$ ? Quels en sont ses paramètres ?

    2. Déterminer l'espérance de la variable aléatoire $Y$.
      Interpréter le résultat en termes de planches non conformes.

    3. L'architecte d'intérieur souhaite que le lot de 250 planches contienne au plus 10 planches non conformes.
      Déterminer la probabilité qu'un lot de 250 planches contienne au plus 10 planches non conformes. On donnera la valeur arrondie au millième.

La société « RADIALTOP » fabrique des pneus de deux catégories, la catégorie "pneu hiver" et la catégorie "pneu 4 saisons".
Pour améliorer la sécurité, le fabriquant effectue des tests de qualité :

Le site de vente en ligne de pneumatiques "PNEUTOP" dispose de pneus venant de ce fabriquant.

Partie A

Un client commande un pneu sur le site "PNEUTOP". On dispose de l'information supplémentaire suivante sur le stock de pneus du site : 25% des commandes concernent les pneus hiver.
On note :

  1. Représenter la situation à l'aide d'un arbre pondéré de probabilité.

  2. Montrer que $P(Q)=0,9675$.

  3. Sachant que le pneu choisi a réussi les tests de qualité, quelle est la probabilité que ce pneu soit un pneu hiver ? Arrondir le résultat au millième.

Partie B

On admet que le nombre de pneus 4 saisons vendus par mois par le site « PNEUTOP » peut être modélisé par une variable aléatoire qui suit la loi normale de moyenne $\mu=450$ et d'écart type $\sigma=15.1$.

    1. Déterminer $P(435\le Y\le 465)$. Arrondir le résultat au centième.

    2. Interpréter le résultat par une phrase.

  2. Le responsable du site veut connaître le nombre $n$ de pneus 4 saisons qu'il doit avoir en stock en début de mois pour que la probabilité d'être en rupture de stock en cours de mois soit inférieure à 0,05.
    Déterminer la plus petite valeur de $n$ remplissant cette condition.

  3. Afin d'optimiser les stocks, le responsable du site aimerait savoir quelle valeur $a$ choisir de sorte que $P(450-a\le X\le 450+a)=0.99$.
    Trouver cette valeur $a$ pour la transmettre au technicien.

Partie C

Le responsable du site « PNEUTOP » commande en début de mois 150 pneus hiver afin de reconstituer son stock.
On considère la variable aléatoire $X$ qui à tout prélèvement de 150 pneus hiver chez le fabriquant associe le nombre de pneus hiver n'ayant pas réussi le test qualité. Le stock de la société « RADIALTOP » est assez important pour assimiler ce prélèvement à un tirage avec remise.

  1. Justifier que la variable aléatoire $X$ suit une loi binomiale dont on donnera les paramètres.

  2. Calculer la probabilité pour que, dans le lot reçu par le responsable du site, il y ait exactement cinq pneus hiver n'ayant pas réussi le contrôle qualité. Arrondir le résultat au millième.

  3. Calculer la probabilité pour que le lot reçu par le responsable du site contienne au moins dix pneus hiver n'ayant pas réussi le contrôle qualité. Arrondir le résultat au millième.

Une usine fabrique des tiges métalliques servant à la fabrication de branche de lunettes.

Partie A

On prélève au hasard des pièces dans la production d'une journée. On suppose que la probabilité qu'une pièce soit défectueuse est 0.1.
On note $X$ la variable aléatoire qui, à tout échantillon de 50 tiges, prélevé au hasard avec remise, associe le nombre de tiges défectueuses parmi les 50.

  1. Expliquer pourquoi $X$ suit une loi binomiale. Donner les paramètres de cette loi.

  2. Déterminer une valeur approchée arrondi à $10^{-4}$ de la probabilité d'un tel échantillon :

    1. de n'avoir aucune pièce défectueuse.

    2. d'avoir au plus 2 pièces défectueuses.

Partie B

On considère maintenant que la variable aléatoire $Y$ qui à toute tige de la production, associe sa longueur suit la loi normale de moyenne $\mu=80$ et d'écart type $\sigma=2.5$.
Dans ce qui suit, on donnera pour chaque résultat une valeur approchée arrondie à $10^{-4}$ près.

  1. Quelle est la probabilité qu'une tige prise au hasard dans la production ait une longueur comprise entre 77.5 et 82.5 ?

  2. On accepte les pièces dont la longueur appartient à l'intervalle [77;86] (les pièces trop longues peuvent être redécoupées).

    1. Quelle est la probabilité qu'une pièce soit acceptée ?

    2. Donner une estimation du pourcentage de pièces défectueuses dans la production.

Les résultats seront à arrondi à $10^{-3}$ près.
Une machine fabrique en grande série des pièces cylindriques. Les diamètres de ces pièces sont exprimés en millimètres.

  1. Soit $X$ la variable aléatoire qui, à chaque pièce prélevée au hasard dans la production, associe son diamètre. On admet que la variable aléatoire $X$ suit la loi normale de moyenne $\mu=50$ et d'écart type $\sigma=0.4$.
    Une pièce est considérée comme défectueuse si son diamètre est inférieur à 49.1 ou supérieur à 50.9.
    Déterminer la probabilité qu'une pièce soit défectueuse.

  2. On suppose dans cette question que 2% des pièces produites sont défectueuses. On effectue un prélèvement de $n$ pièces prises au hasard dans la production. Ce prélèvement peut être assimilé à un tirage avec remise.
    On désigne par $Y$ la variable aléatoire qui, à tout échantillon de $n$ pièces ainsi réalisé, associe le nombre de pièces défectueuses dans l'échantillon.

    1. Quelle est la loi suivie par $Y$ ?

    2. Pour $n=10$, calculer la probabilité $P(Y=2)$.

    3. Le client accepte un lot de 10 pièces s'il contient au plus une pièce défectueuse. Quelle est la probabilité que le lot soit accepté.

  3. Pour contrôler la fabrication, on prélève des échantillons de 2500 pièces ; ce prélèvement est assimilé à un tirage avec remise.
    On appelle $\overline{X}$ la variable aléatoire qui, à tout échantillon de 2500 pièces, associe la moyenne des diamètres des pièces de cet échantillon.

    1. Pourquoi $\overline{X}$ suit à peu près la loi normale de moyenne 50 et d'écart type 7.

    2. Déterminer le nombre réel $b$ positif tel que $P(50-b \le X \le 50+b)=0.99$.

Partie A

Une entreprise fabrique en grande quantité des clés USB. Les clés USB produites peuvent présenter deux défauts : le défaut A et le défaut B. On sait que :

On appelle $A$ l'évènement "la clé USB présente le défaut A" et $B$ l'évènement "la clé USB présente le défaut B".

  1. Calculer la probabilité que la clé USB présente le défaut A.

  2. Calculer la probabilité que la clé USB présente le défaut B sachant qu'elle a le défaut A.

  3. Calculer la probabilité que la clé USB présente le défaut B ou le défaut A.

  4. Les événements $A$ et $B$ sont-ils indépendants ?

Partie B

Les clés USB sont commercialisées par lot de 1000. On prélève au hasard un lot de 1000 dans un dépôt de l'entreprise.
On assimile ce prélèvement à un tirage avec remise de 1000 clés USB.
On considère la variable aléatoire $Y$ qui, à tout prélèvement de 1000 clés USB, associe le nombre de clés USB présentant un défaut parmi ces 1000 clés USB.
On admet que la variable aléatoire $Y$ suit la loi binomiale de paramètres $n=1000$ et $p=0,107$.
On décide d'approcher la loi de la variable aléatoire discrète $Y$ par la loi normale de moyenne 107 et d'écart-type 9,78. On note $Z$ la variable aléatoire suivant cette loi normale.

  1. Justifier les paramètres de la loi normale suivie par $Z$.

  2. Calculer la probabilité qu'il y ait au plus 95 clés USB présentant un défaut dans le lot de 1000 clés USB, c'est-à-dire calculer $P(Z\le 95,5)$.

Dans tout l'exercice, les probabilités seront arrondies au millième.
Une entreprise qui assemble des ordinateurs achète et stocke un certain type de composants informatiques. Le but de cet exercice est d'étudier certains aspects liés à ces composants.
Les parties A, B et C peuvent être traitées de façon indépendante.

Partie A

L'entreprise achète les composants auprès de deux fournisseurs nommés A et B.
Le fournisseur A lui procure 60% de ses composants, le reste provient du fournisseur B.
Une étude statistique révèle que 0,5% des composants provenant du fournisseur A sont défectueux et que 1% de ceux provenant du fournisseur B le sont également.
On prélève au hasard un composant dans le stock de l'entreprise.
On note $A$ l'évènement « le composant provient du fournisseur A » et $D$ l'évènement « le composant est défectueux ».

  1. Traduire les données de l'énoncé dans un arbre de probabilités à l'aide des évènements $A$ et $D$.

  2. Calculer la probabilité de l'évènement $D$.

  3. Sachant que le composant prélevé est défectueux, quelle est la probabilité qu'il provienne du fournisseur B ?

Partie B

Dans cette partie, on admet que 0,7% des composants du stock de l'entreprise sont défectueux.
Un technicien prélève au hasard 50 composants dans ce stock pour réaliser des assemblages.
On considère que le stock est assez important pour qu'on puisse assimiler ce prélèvement de 50 composants à un tirage avec remise. On note $X$ la variable aléatoire qui, parmi les 50 composants prélevés, comptabilise le nombre de composants défectueux.

  1. Quelle est la loi de probabilité de la variable aléatoire $X$ ? Justifier et donner ses paramètres.

  2. Calculer la probabilité que le prélèvement ne comporte aucun composant défectueux.

  3. Calculer la probabilité que le prélèvement comporte au plus un composant défectueux.

  4. Calculer la probabilité que le prélèvement comporte entre 1 et 4 composants défectueux.

Partie C

Pour un certain type d'assemblage, le besoin journalier d'un technicien de l'entreprise, en nombre de composants, peut être modélisé par une variable aléatoire $Y$ qui suit la loi normale de paramètres $\mu=100$ et $\sigma=10$.

  1. Quelle est la probabilité qu'un jour donné le technicien ait besoin de plus de 110 composants ?

  2. Au début d'une journée, le technicien constate qu'il n'y a plus que 90 composants en stock. Quelle est la probabilité que, ce jour-là, il ne puisse pas finir son travail ?

  3. Afin d'optimiser les stocks, le technicien aimerait savoir quelle valeur $a$ choisir de sorte que $P(100-a \le X \le 100+a)=0.98$. Trouver cette valeur $a$ pour la transmettre au technicien.

Théorème central limit

On considère un lot de tubes à essais.
À chaque tube prélevé au hasard, on associe son diamètre et sa hauteur exprimés en millimètres. On définit ainsi deux variables aléatoires $D$ et $H$.
La variable aléatoire $D$ suit la loi normale de moyenne $\mu_D=19.7$ et d'écart type $\sigma_D=0.4$.
La variable aléatoire $H$ suit la loi normale de moyenne $\mu_H=203$ et d'écart type $\sigma_H=6$.
On suppose que les variables aléatoires $D$ et $H$ sont indépendantes.

  1. Calculer, à $10^{-3}$ près, la probabilité qu'un tube à essais ait un diamètre inférieur à 20 mm.

  2. Calculer, à $10^{-3}$ près, la probabilité qu'un tube à essais ait une hauteur supérieure à 195 mm.

  3. Des contraintes d'expérience et d'entretien imposent les conditions suivantes : le diamètre doit appartenir à l'intervalle $[19;20.5]$ et la hauteur, à l'intervalle $[195;210]$.
    Calculer la probabilité de l'événement "$19\le D\le 20.5$ et $195\le H\le 210$".
    Estimer le pourcentage de tubes à essais utilisables.

Les résultats seront à arrondi à $10^{-3}$ près.
Pour la réalisation d'un projet, une société doit effectuer successivement deux tâches A et B. Les durées de réalisation de ces tâches sont aléatoires. On désigne par $X$ (respectivement par $Y$) la variable aléatoire qui, à une tâche de type A tirée au hasard (respectivement une tâche de type B), associe sa durée exprimée en semaines.
Ces variables aléatoires sont indépendantes et suivent des lois de probabilité approchées par les lois normales : de moyenne 22 et d'écart type 3 pour $X$, de moyenne 25 et d'écart type 4 pout $Y$.

  1. Déterminer la probabilité de réaliser une tâche de type A en plus de 30 semaines.

  2. Soit $u$ un réel positif. On considère l'événement $E$ : "$25-u\le Y\le 25+u$".
    Déterminer l'ensemble des valeurs de $u$ pour lesquelles on a : $P(E)\ge 0.9544$.

  3. On désigne par $Z$ la variable aléatoire qui, à tout projet tiré au hasard, associe sa durée, exprimée en semaines.

    1. Calculer l'espérance mathématique et l'écart type de $Z$.

    2. On admet que $Z$ suit une loi proche de la loi normale $\mathcal{N}(47;5)$.
      Déterminer la probabilité de réaliser le projet en moins de 50 semaines.

Partie B

On considère maintenant que la variable aléatoire $Y$ qui à toute tige de la production, associe sa longueur suit la loi normale de moyenne $\mu=80$ et d'écart type $\sigma=2.5$. (l'unité n'est précisée)
Dans ce qui suit, on donnera pour chaque résultat une valeur approchée arrondie à $10^{-4}$ près.

  1. Quelle est la probabilité qu'une tige prise au hasard dans la production ait une longueur comprise entre 77.5 et 82.5 ?

  2. On accepte les pièces dont la longueur appartient à l'intervalle $[77;86]$ (les pièces trop longues peuvent être redécoupées).

    1. Quelle est la probabilité qu'une pièce soit acceptée ?

    2. Donner une estimation du pourcentage de pièces défectueuses dans la production.

Dans une revue, on peut lire :"on estime à 60.5% le pourcentage de Français partant au moins une fois en vacances dans le courant de l'année". On considère, 100 personnes prises au hasard, avec remise, parmi la population française. Dans ce qui suit, tous les résultats seront arrondis à $10^{-3}$ près.

  1. On désigne par $X$ la variable aléatoire qui à chaque prélèvement de 100 personnes associe le nombre de celles qui ne partent pas en vacances dans le courant de l'année.

    1. Justifier que la loi de probabilité suivie par la variable X est une loi binomiale. On précisera les paramètres de cette loi.

    2. Calculer l'espérance mathématique et l'écart type de cette variable $X$.

    3. Calculer la probabilité de l'événement $X=45$.

  2. On décide d'approcher la loi de la variable aléatoire discrète X par la loi normale de paramètres $\mu=39.5$ et $\sigma=4.89$. On note $Y$ une variable aléatoire suivant la loi $\mathcal{N}(39.5;4.89)$.
    Justifier la valeur de ces paramètres.

  3. En utilisant cette approximation (et la correction de continuité !), calculer :

    1. La probabilité que 45 personnes exactement parmi les 100 ne partent pas en vacances dans le courant de l'année en appliquant la correction de continuité.

    2. La probabilité qu'au plus 30 de ces 100 personnes ne partent as en vacances dans le courant de l'année.

Les résultats seront à arrondi à $10^{-3}$ près. Une machine fabrique en grande série des pièces cylindriques. Les diamètres de ces pièces sont exprimés en millimètres.

  1. Soit $X$ la variable aléatoire qui, à chaque pièce prélevée au hasard dans la production, associe son diamètre. On admet que la variable aléatoire $X$ suit la loi normale de moyenne $\mu=50$ et d'écart type $\sigma=0.4$.
    Une pièce est considérée comme défectueuse si son diamètre est inférieur à 49.1 ou supérieur à 50.9.
    Déterminer la probabilité qu'une pièce soit défectueuse.

  2. On suppose dans cette question que 2% des pièces produites sont défectueuses. On effectue un prélèvement de $n$ pièces prises au hasard dans la production. Ce prélèvement peut être assimilé à un tirage avec remise.
    On désigne par $Y$ la variable aléatoire qui, à tout échantillon de $n$ pièces ainsi réalisé, associe le nombre de pièces défectueuses dans l'échantillon.

    1. Quelle est la loi suivie par $Y$ ?

    2. Pour $n=10$, calculer la probabilité $P(Y=2)$.

    3. Le client accepte un lot de 10 pièces s'il contient au plus une pièce défectueuse. Quelle est la probabilité que le lot soit accepté ?

  3. Pour contrôler la fabrication, on prélève des échantillons de 2500 pièces ; ce prélèvement est assimilé à un tirage avec remise.
    On appelle $\overline{X}$ la variable aléatoire qui, à tout échantillon de 2500 pièces, associe la moyenne des diamètres des pièces de cet échantillon.

    1. Pourquoi $\overline{X}$ suit à peu près la loi normale de moyenne 50 et d'écart type 7.

    2. Déterminer le nombre réel $b$ positif tel que $P(50-b \le \overline{X} \le 50+b)=0.99$.

Demander le programme !

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲