Savoir calculer une image ou un antécédent
Savoir calculer une image
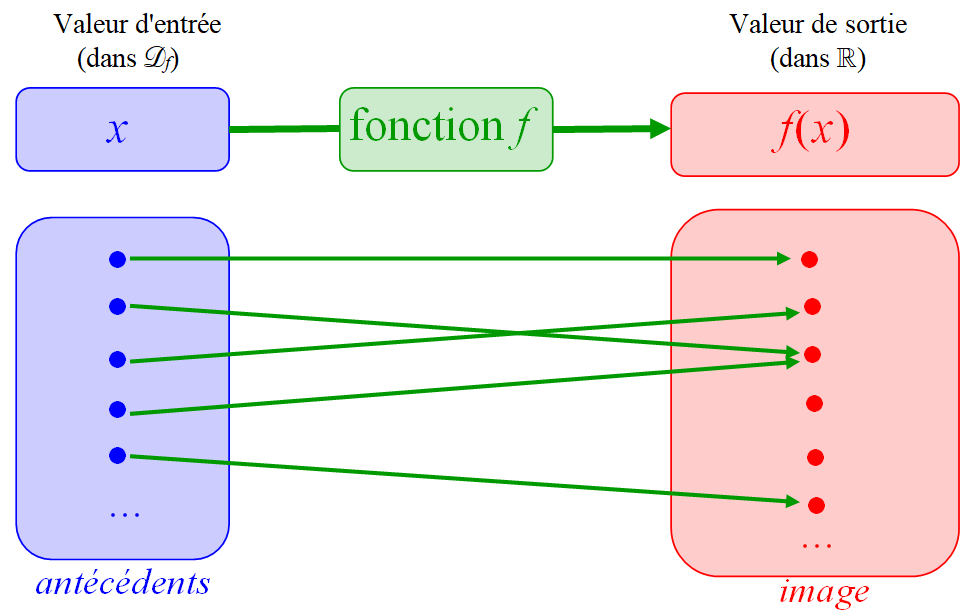
Notons $\mathcal{D_f}$ un intervalle ou une réunion d’intervalles de $\mathbb{R}$.
On définit une fonction $f$ de $\mathcal{D_f}$ dans $\mathbb{R}$ en associant à chaque réel $x$ de $\mathcal{D_f}$ un unique
réel noté $f(x)$.
Cette fonction $f$ est alors notée : $f:x\mapsto f(x)$.
-
$x$ s'appelle la variable.
-
$f(x)$ s′appelle l'image de $x$ par $f$ ; elle est toujours unique.
-
$\mathcal{D_f}$ est appelé ensemble de définition.
-
Si $\color{red}{y}=f(\color{blue}{x})$ alors $\color{blue}{x}$ est un antécédent de $\color{red}{y}$ par $f$ ; il n’est pas forcément unique.
En SNIR, la variable est le plus souvent notée $t$ car cette variable représentera souvent le temps.
La partie inscriptible d'un CD audio est une couronne de rayons 25 mm et 55 mm. Un faisceau laser lit la musique en
allant de l'intérieur de cette couronne vers l'extérieur.
On note $x$ la distance en millimètre du laser au bord du cercle intérieur après lecture d'une partie de la musique.
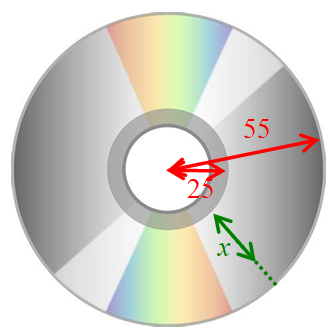
On admet si le rayon maser se trouve à $x$ millimètres du bord du cercle intérieur alors $D(x)$ minutes de musique ont été jouées avec $D(x)=\dfrac{x^2+50x}{30}$.
La durée de musique jouée peut être modélisée par une fonction notée ici $D$ telle que :
-
La variable de la fonction est $x$, valeur correspondant à la distance au bord intérieur.
-
L'ensemble de définition est l'intervalle $[0;30]$ : $x$ peut être n'importe quel nombre réel entre 0 et 30.
-
L'image de $x$ correspond au résultat du calcul $\dfrac{x^2+50x}{30}$.
-
On peut noter : $D:x\mapsto\dfrac{x^2+50x}{30}$.
-
$D(10)=20$. Cela signifie :
-
$20$ est l'image de $10$ par $D$ : si on sait que le rayon laser est à 10 mm du bord intérieur alors la musique a déjà été jouée 20 minutes.
-
$10$ est un antécédent de $20$ par $D$ : si on sait que la musique a déjà été jouée 20 minutes alors le rayon laser est à 10 mm du bord intérieur.
-
Soit $f$ une fonction définie sur un intervalle $I$ de $\mathbb{R}$.
Soit $a$ un réel de cet intervalle $I$.
Pour calculer l’image de $a$ par $f$, il suffit de remplacer tous les $x$ par $a$ dans l'expression de $f(x)$.
Reprenons la fonction $D:x\mapsto \dfrac{x^2+50x}{30}$.
Pour calculer l'image de $30$, image notée $D(30)$, il suffit de remplacer $x$ par 30 donc de calculer
$\dfrac{30^2+50\times 30}{30}$. D'où :
$D(30)=\dfrac{30^2+50\times 30}{30}=\dfrac{900+1500}{30}=\dfrac{2400}{30}=80$.
L'image de $30$ par $D$ est $80$.
Cela signifie concrètement qu'à 30 mm du bord intérieur (donc au bout de la piste de lecture) la musique a été jouée
pendant 80 minutes.
-
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(t)=(2t-3)^2+4$.
Calculer l'image de 5 par $f$. -
On considère la fonction $g$ définie par $g(t)=\dfrac{t^2+5}{t-5}$.
-
Calculer l'image de 3 par $g$.
-
Que se passe-t-il lorsque l'on veut calculer l'image de 5 par $g$ ? Qu'en penser ?
-
-
On considère la fonction $h$ définie par $h(t)=\dfrac{2t+5}{(2t+1)(3-t)}$.
Calculer l'image de 2 par $h$.
-
L'affectation sur Xcas se réalise à l'aide de
:=. -
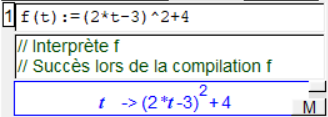
Pour entrer sur Xcas la fonction $f$ définie par $f(t)=(2t-3)^2+4$, il suffit de saisir
f(t):=(2*t-3)^2+4.
-
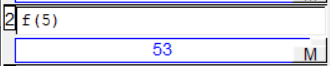
Pour calculer l'image de $5$ par $f$, il suffit ensuite de saisir sur Xcas
f(5).
-
Commencer par entrer la fonction dans un exercice de BTS portant sur une fonction est un réflexe à acquérir pour le CCF.
-
Vérifier toujours que l'affichage renvoyé en bleu correspond bien à la fonction que vous avez voulu rentrer.
Reprendre les calculs d'image demandés à l'exercice précédent mais cette fois-ci sur Xcas.
Soit $f$ la fonction définie sur $[0;+\infty[$ par $f(t)=\sqrt{5t}+2t-3$.
-
Calculer l'image de 20 par $f$.
-
Calculer $f(45)$.
-
Est-il vrai que 24 est l'image de 10 par $f$ ?
Le vin est issu de la fermentation du jus de raisin : le sucre de ce jus est transformé en alcool.
Ainsi, il est important pour un vigneron de connaître lors des vendanges la teneur en sucre du jus de ses raisins.
Pour cela, il utilise un mustimètre. Cet appareil permet de mesurer la masse volumique $m$ du jus de raisin (en $g/dm^3$)
et permet d'en déduire la teneur en $t$ en sucre du jus de raisin ($t$ est exprimée en $g/L$).
On admet que $t$ et $m$ sont liés par la formule suivante :
-
Quelle est l'expression de fonction $f$ qui associe à la masse volumique $m$ la teneur en sucre $t$ ?
-
Calculer l'image de 1090 par $f$. Quelle est la signification concrète du nombre obtenu ?
-
Voici des données trouvées sur Internet :
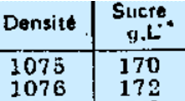
Les données présentes dans le tableau sont-elles correctes ?
Certains auteurs attribue la création du premier mustimètre à la philosophe, physicienne et mathématicienne antique Hypatie (IVè siècle de notre ère).
Savoir calculer un antécédent
Soit $f$ une fonction définie sur un intervalle $I$ de $\mathbb{R}$.
Pour calculer les antédécents d'un réel $a$ par $f$, il suffit de résoudre l'équation $f(x)=a$ en limitant les valeurs possibles de $x$ à l'intervalle $I$.
Reprenons la fonction $D:x\mapsto \dfrac{x^2+50x}{30}$.
Pour calculer les antécédents de $59.2$, il suffit de résoudre l'équation
$\dfrac{30^2+50\times 30}{30}=59.2$.
Pour solve((x^2+50x)/30=59.2,x), Xcas renvoie [-0.7400000000000e2,24.0].
Comme la fonction $D$ est définie sur l'intervalle $[0;30]$, seule la solution positive 24 est correcte.
24 est donc l'antécédent de 59.2 par $D$.
Cela signifie concrètement que 59 minutes et 12 secondes (=59.2 minutes) ont été écoutées lorsque le laser se trou à 24
millimètres du bord intérieur.
-
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(t)=(2t-3)^2+4$.
Calculer les antécédents de 5 par $f$. -
On considère la fonction $g$ définie par $g(t)=\dfrac{t^2+5}{t-5}$.
Calculer l'image de -7 par $f$.-
Calculer les antécédents de -7 par $g$.
-
Que se passe-t-il lorsque l'on veut calculer les antécédents de 7 par $g$ ?
-
-
On considère la fonction $h$ définie par $h(t)=\dfrac{2t+5}{(2t+1)(3-t)}$.
Calculer les antécédents de $-\frac{3}{4}$ par $h$.
Soit la fonction $h$ donnant la hauteur par rapport au sol, en mètres, d'une balle lancée en l'air en fonction du temps $t$, exprimé en seconde. On admet que $h$ est définie sur $[0;6]$ par $h(t)=6t−t^2$.
-
Quelle est l'image de 1 par $h$ ?
-
Quels sont les antécédents de 8 par $h$ ?
-
On admet que la hauteur maximale est atteinte 3 secondes après le lancer. Déterminer la hauteur maximale atteinte par la balle.
-
Déterminer les instants où la balle au niveau du sol.
Pour réaliser la correspondance entre l'âge $c$ d'un chat, en années, et l'âge $h$ équivalent humain en années, on peut utiliser la relation suivante : $h=\dfrac{5c(c+1)^3}{c^3+1}$.
-
Déterminer la fonction $f$ qui associe à l'âge $c$ d'un chat l'âge humain correspondant.
-
Déterminer l'image de 0.5 par $f$.
Quelle interprétation concrète pouvez-vous faire ? -
Déterminer l'antécédent de 30 par $f$.
Quelle interprétation concrète pouvez-vous faire ? -
Quel est l'âge d'un chat correspondant à votre âge de 20 ans (environ) ?
La hauteur $h(t)$ d'un plan de blé expérimental est donnée au bout de $t$ mois par $h(t)=\dfrac{t}{t+2}$.
-
Quelle est la taille de ce plan de blé au bout de 6 mois ?
-
Combien de temps faut-il attendre pour que le plan de blé atteigne 50 cm ?
-
Le plan de blé est arrivé à maturité lorsqu'il atteint une taille de 80 cm.
Au bout de combien de mois, le plan pourra-t-il être fauché ?
-
On considère ici la fonction $h$ qui associe au temps $t$ la hauteur $\dfrac{t}{t+2}$, c'est-à-dire la fonction $h:t\mapsto\dfrac{t}{t+2}$.
Dans cette première question, on connaît le temps et l'on cherche la hauteur : il suffit de calculer l'image de 6 par $f$.$f(3)=\dfrac{6}{6+2}=\dfrac{3}{4}$.
La taille de ce plan de blé au bout de 6 mois est de 0.75 mètre.
-
Dans cette première question, on connaît la hauteur et l'on cherche le temps : il suffit de calculer les antécédents de 0.5 par $f$.
solve(t/(t+2)=0.5,t)renvoie2.0.Il faut donc attendre 2 mois pour que le plan de blé atteigne 50 cm.
-
Dans cette question encore, on connaît la hauteur et l'on cherche le temps : il suffit de calculer les antécédents de 0.8 par $f$.
solve(t/(t+2)=0.8,t)renvoie8.0.Le plan pourra être fauché au bout de 8 mois.
Savoir lire une image ou antécédent
Soit $f$ une fonction définie sur un intervalle $\mathcal{D}_f$.
Dans un repère, la courbe représentative $\mathcal{C}_f$ de la fonction $f$ est l’ensemble des points $M$ de coordonnées $(x;y)$ où :
-
$x\in\mathcal{D}_f$ : $x$ est une abscisse possible,
-
$y=f(x)$ : l'ordonnées est l'image par $f$ de l'abscisse.
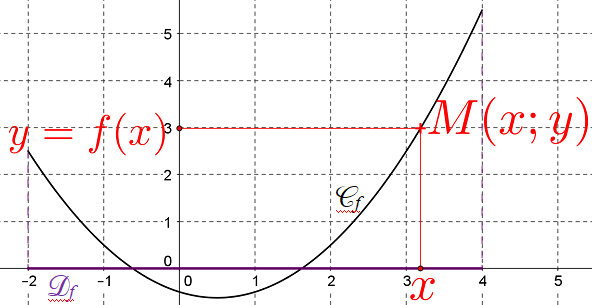
Voici les méthodes pour lire les images et les antécédents d'un réel "a" par une fonction :
-
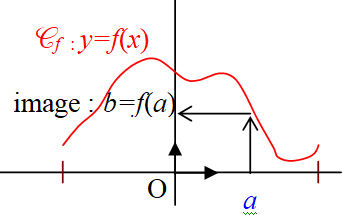
Lecture de l'image de $a$ par $f$ dans un repère orthogonal :
-
on repère $a$ sur l’axe des abscisses,
-
puis on trace la verticale jusqu’à la courbe $\mathcal{C}_f$,
-
enfin, on lit l’image sur l’axe des ordonnées.
-
-
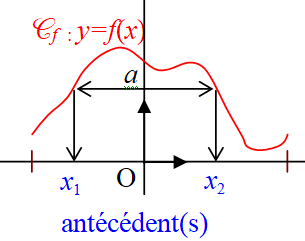
Lecture des antécédents de $a$ par $f$ dans un repère orthogonal :
-
on repère $a$ sur l’axe des ordonnées,
-
puis on trace la droite horizontale passant par $a$ jusqu’à la courbe $\mathcal{C}_f$,
-
enfin, on lit les antécédents comme abscisse des points d'intersection éventuels.
-
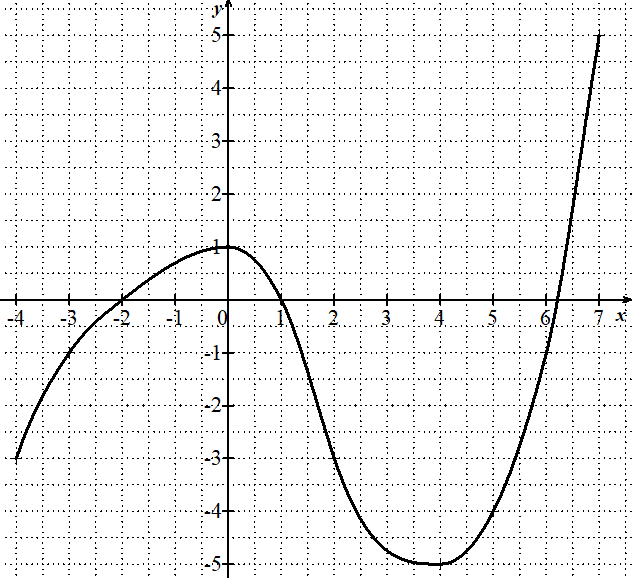
Voici ci-dessous la courbe d'une fonction représentant une fonction $f$.
-
L'ensemble de définition de $f$ est l'intervalle [-4;7] : c'est l'ensemble des abscisses possibles pour les points de la courbe représentant $f$.
-
L'image de 2 est -3.
-
L'antécédent de 2 est proche de 6.5.
-
L'image de 0 est 1.
-
Les antécédents de 0 sont -2, 1 et vers 6.2.
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(t)=t^3-2t$.
-
Tracer sur Geogebra une courbe représentant la fonction $f$.
-
-
Lire graphiquement l'image de 1 par $f$.
-
Vérifier par un calcul à la main ou sur Xcas.
-
-
-
Lire graphiquement les antécédents de 1 par $f$.
-
Vérifier par un calcul sur Xcas.
-
-
-
Lire graphiquement l'image de 0 par $f$.
-
Vérifier par un calcul à la main ou sur Xcas.
-
-
-
Lire graphiquement les antécédents de 0 par $f$.
-
Vérifier par un calcul à la main ou sur Xcas.
-
-
-
Tracer dans le même repère la courbe représentant la fonction $g$ définie par $g(t)=-t$.
-
Résoudre graphiquement l'équation $f(t)=g(t)$.
En sélectionnant l'icone intersection
 ,
puis en cliquant sur chacune des courbes représentant les fonctions, les coordonnées des
points d'intersection apparaissent dans la partie Algèbre.
,
puis en cliquant sur chacune des courbes représentant les fonctions, les coordonnées des
points d'intersection apparaissent dans la partie Algèbre.
-
Reza est passager d'une voiture se déplaçant sur une très longue ligne droite. Il part du kilomètre 0.
À un kilomètre du kilomètre 4 de cette route, se trouve l'antenne-relais d'un opérateur téléphonique.
On admet que l'intensité du signal reçu par le télphone de Reza est donnée par $f(x)=\dfrac{10}{1+(4-x)^2}$, où $x$ correspond au nombre de kilomètres parcourus depuis le kilomètre 0.
-
Représenter la courbe représentant la fonction $f$ sur Geogebra.
-
-
Lire graphiquement l'image de 2 par $f$.
-
Vérifier par un calcul à la main ou sur Xcas.
-
-
-
Lire graphiquement les antécédents de 8 par $f$.
-
Vérifier par un calcul à la main ou sur Xcas.
-
-
L'intensité reçue est suffisante pour que le téléphone portable de Reza s'y connecte quand cette intensité atteint au moins la valeur de 4.
Déterminer la longueur de la route sur laquelle le téléphone de Reza peut se connecter à l'antenne-relais.
Savoir déterminer le signe d'une fonction
Savoir lire le signe d'une fonction
Voici la représentation graphique $\mathcal{C}_f$ de la fonction $f:t\mapsto \dfrac{1}{12}(t+1) (2t -4) (6-t)$ :
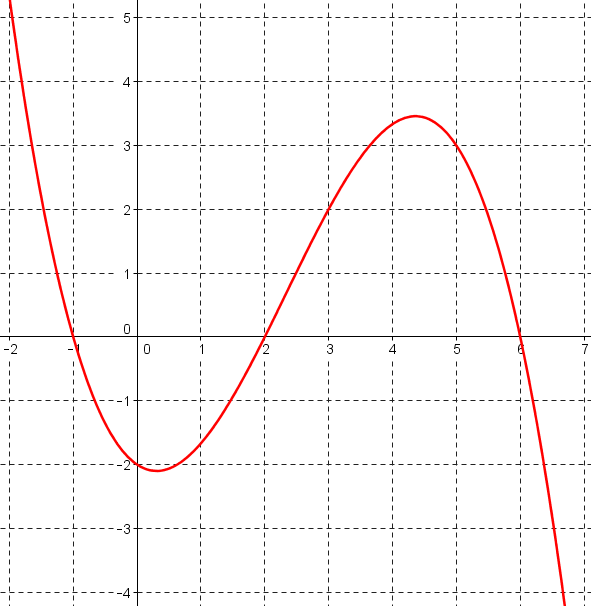
-
Les images $f(t)$ se lisant sur l'axe des ordonnées, chercher quand les images sont nulles revient à chercher les abscisses des points où la courbe $\mathcal{C}_f$ coupe l'axe des abscisses.
Ainsi, $f(t)=0$ lorsque $t\in \{-1;2;6\}$.
-
Les images $f(t)$ se lisant sur l'axe des ordonnées, chercher quand les images sont positives revient à chercher les abscisses des points où la courbe $\mathcal{C}_f$ est au_dessus de l'axe des abscisses.
Ainsi, $f(t)\gt 0$ lorsque $t\in ]-\infty;-1[\cup ]2;6[$.
-
De même, $f(t)\lt 0$ lorsque $t\in ]-1;2[\cup ]6;+\infty[$.
Pour synthétiser ces informations, on peut utiliser un tableau de signes :

Voici la courbe représentant une fonction $f$ : 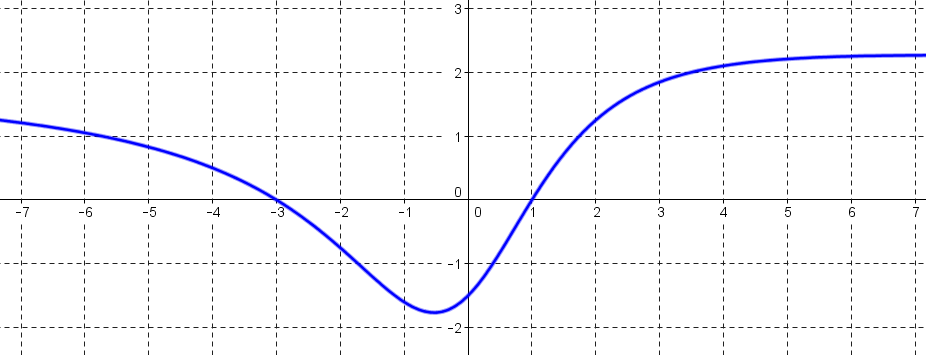
Dresser le tableau de signes de cette fonction $f$.
Voici le tableau de signes demandé : 
Voici la courbe des températures mesurées lors d'une journée d'hiver : 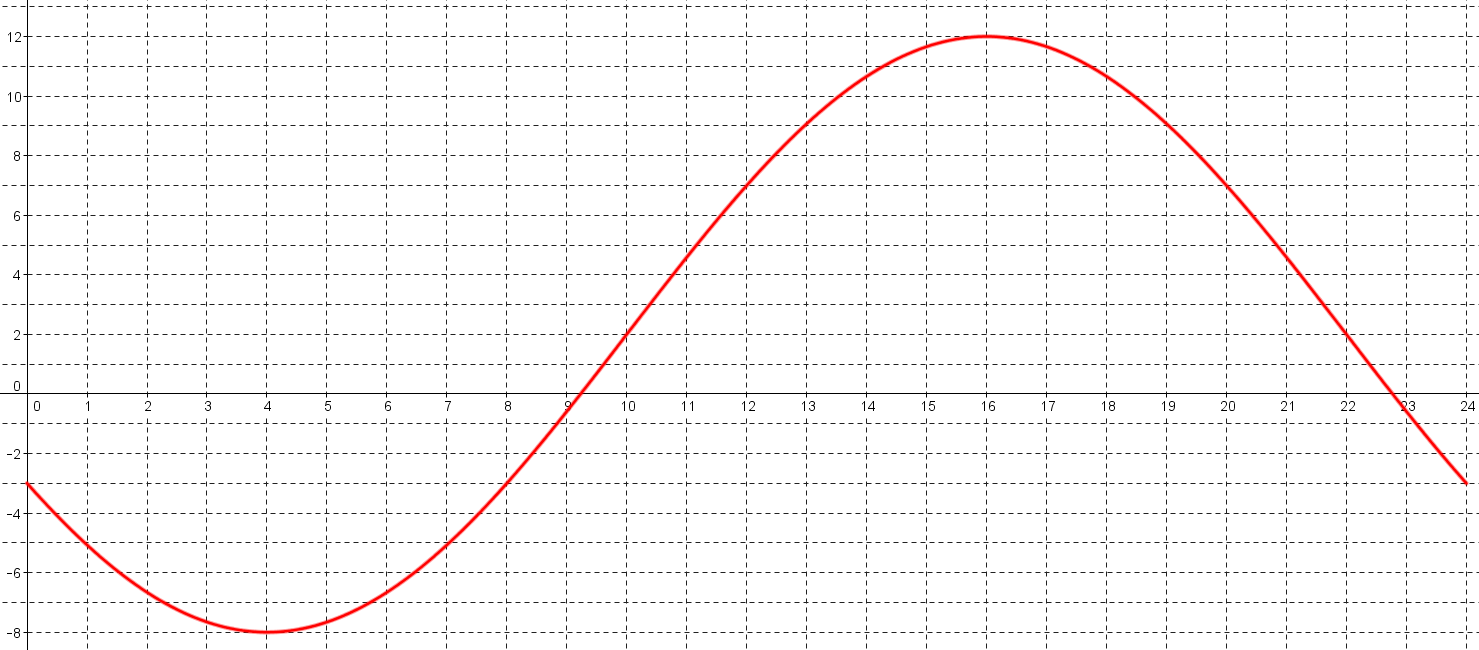
Déterminer l'ensemble des instants où la température fut négative (arrondir à l'heure près).
Pour résoudre graphiquement une inéquation du type $f(t)\gt k$ (avec $k\in \mathbb{R}$), il suffit de :
-
tracer la droite horizontale passant par $k$ (valeur placée sur l'axes des ordonnées),
-
lire les abscisses des points où la courbe représentant $f$ est strictement au-dessus de cette droite.
Voici la courbe représentant une fonction $f$ définie sur $]-\infty;2[\cup]2;+\infty[$ :
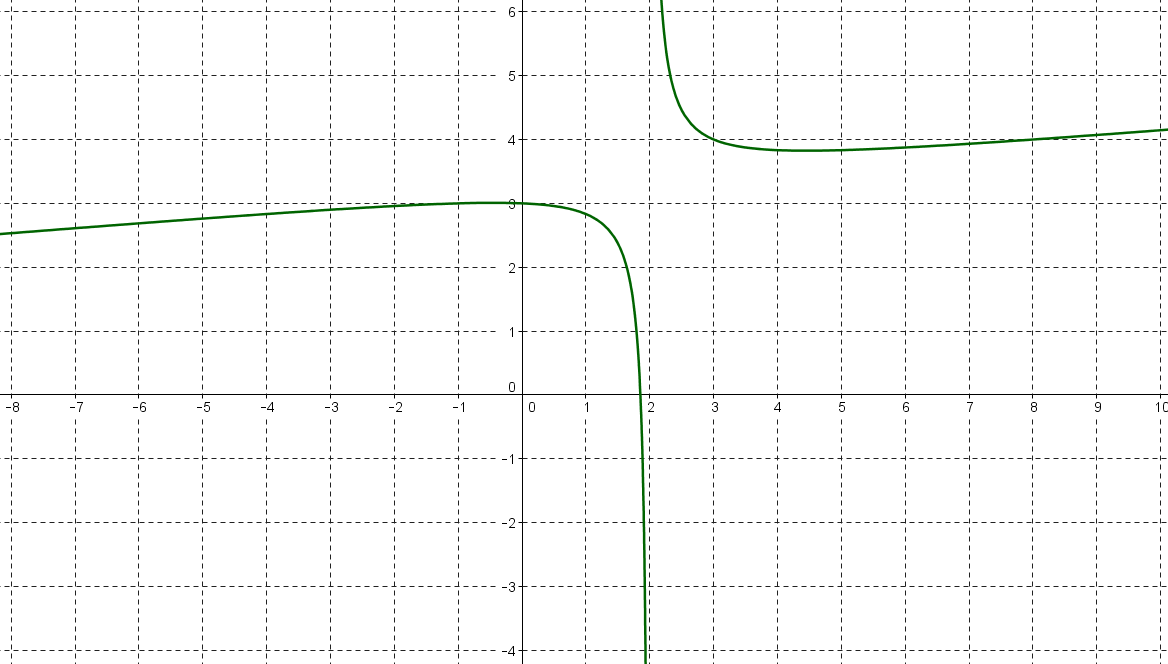
Résoudre graphiquement l'inéquation $f(t)\ge 4$.
Commencer par tracer la droite horizontale d'équation $y=4$ : 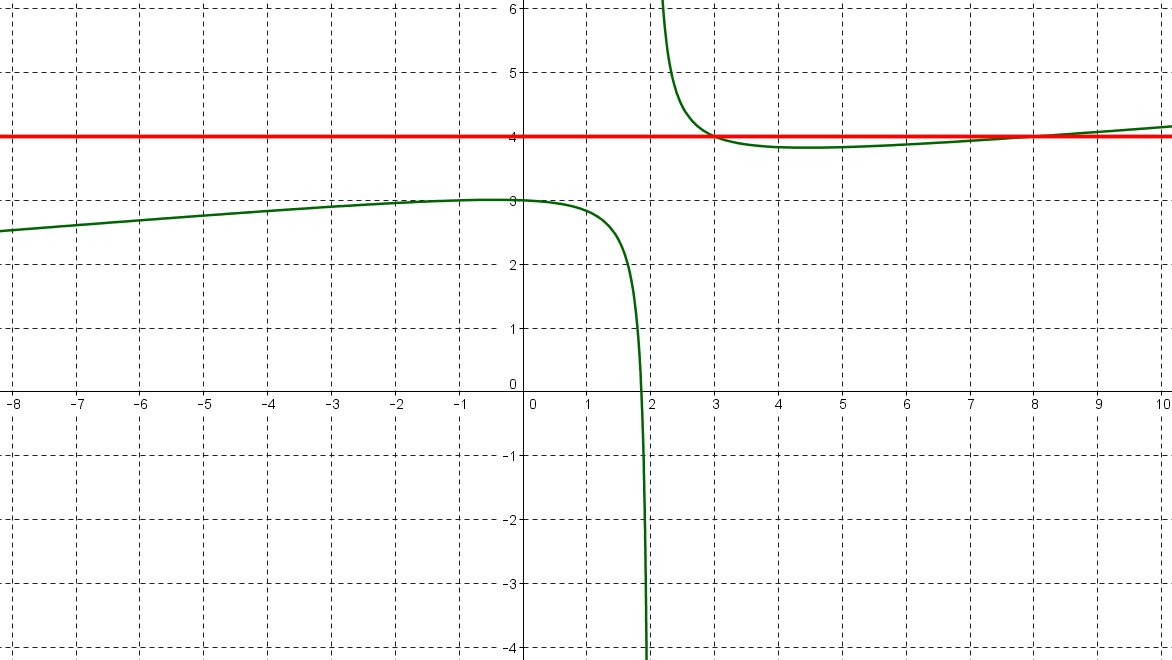
Il y a deux parties de la courbe représentation $f$ qui se trouve au-dessus de la droite horizontale tracée :
-
la partie définie sur l'intervalle $]2;3]$,
-
la partie définie sur l'intervalle $[8;+\infty[$.
Le cannabis est une drogue interdite en France.
Il peut être détecté par les forces de l’ordre par une analyse urinaire à partir d'une concentration de 50 μg/L.
La concentration urinaire de cannabis (molécule TH-CO) en μg/L chez une conductrice ayant fumé un seul joint est
modélisée ci-dessous sur 10 jours ; le temps est exprimé en heures. Nous noterons $f$ la fonction ainsi définie.
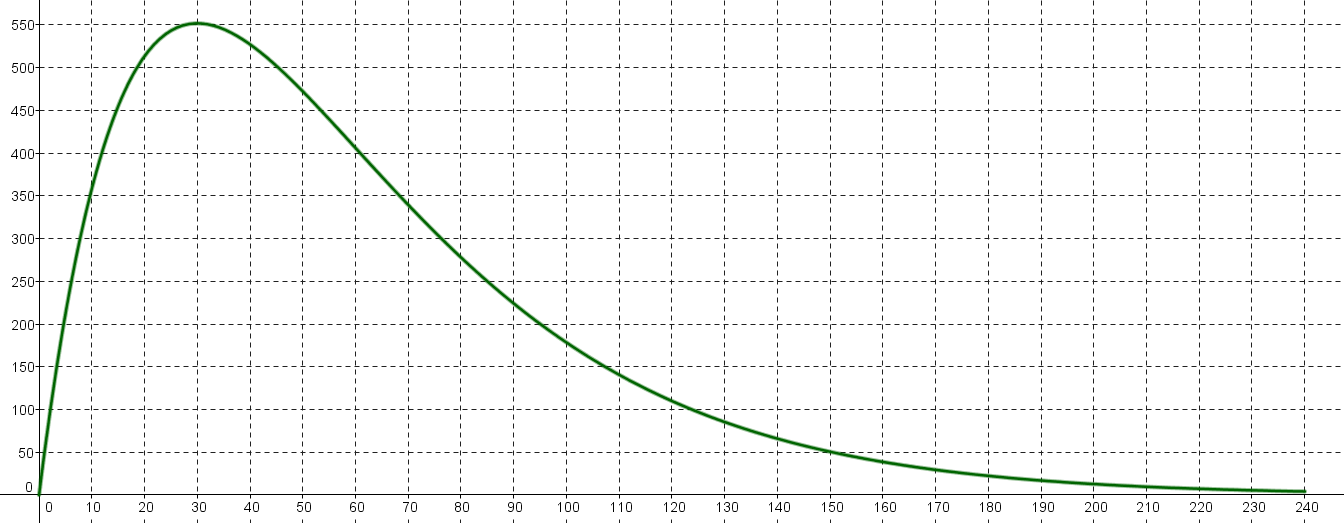
-
Déterminer les instantss le taux atteint 200 μg/L.
-
Pendant combien de jours ce joint laissera des traces dans les urines ?
-
Déterminer la période temporelle où le taux dépasse 450 μg/L.
Soit $f$ et $g$ deux fonctions définies sur un intervalle $I$.
Pour résoudre grpahiquement l'inéquation $f(t)>g(t)$, il suffit de trouver les abscisses des points où la courbe représentant $f$
est strictement au-dessus de celle représentant $g$.
Voici la représentation graphique de deux fonctions $f$ et $g$ :
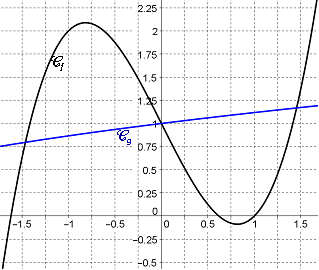
Résoudre graphiquement l'inéquation $f(t)> g(t)$.
La zone violette correspond à l'ensemble des
points où la courbe représentant $f$ est strictement au-dessus de celle représentant $g$.
Les solutions correspondent aux abscisses de ces points ; ces solutions
forment la zone rouge (deux intervalles) : 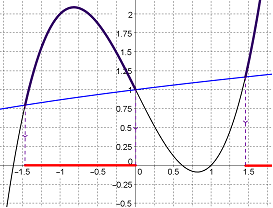
Conclusion sous forme de réunion de deux intervalles : $S=]-1.4;0[\cup]1.4;+\infty[$.
On considère les fonctions $f$ et $g$ définies respectivement sur $\mathbb{R}$ par $f(t)=6t^2+2t−4$ et $g(t)=3t^2+13t−10$.
-
Sur Geogebra, tracer les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ représentant les fonctions $f$ et $g$.
-
Résoudre graphiquement $f(t)=g(t)$ puis $f(t)\lt g(t)$.
-
Résoudre à la main l'équation $f(t)=g(t)$ puis l'inéquation $f(t)\lt g(t)$.
-
Vérifier sur Xcas les solutions précédentes.
Savoir étudier le signe d'une fonction affine
Pour dresser le tableau de signes d'une fonction affine $f:t\mapsto ax+b$, il suffit de :
-
résoudre l'équation $at+b=0$,
-
placer la solution trouvée ($-\dfrac{b}{a}$) dans la première ligne du tableau de signes et le symbole $0$ en-dessous dans la seconde ligne,
-
mettre le signe du coefficient multiplicateur $a$ à "droite du 0".
Ainsi : 
Le tableau de signe de la fonction $f:t\mapsto 3-2t$ est obtenu ainsi :
-
$3-2t=0 \iff 3=2t \iff \dfrac{3}{2}=t$
-
On place cette valeur dans la première ligne du tableau de signes et on ajoute un "0" en-dessous :

-
On met le signe du coefficient multiplicateur à droite du "0" :

-
Dresser le tableau de signe de l'expression $4t-5$.
-
Tracer la courbe représantant la fonction $f:t\mapsto 4t-5$ pour vérifier le tableau de signes.
-
Résoudre sur Xcas l'inéquation $4t-5>0$ pour vérifier le tableau de signes.
Savoir étudier le signe d'un produit ou d'un quotient
Pour étudier le signe d'un produit :
-
On créé un tableau de signes où chaque facteur apparaît dans un ligne différente,
-
on étudie le signe de chacun des facteurs,
-
on utilise la règle des signes pour en déduire le signe du produit dans la dernière ligne.
Étudier le signe du produit $(2t+5)(6-3t)$.
-
Tableau avec un facteur par ligne :

-
Étude du signe de chaque facteur :
$2t+5=0 \iff 2t=-5 \iff t=-\dfrac{5}{2}$
$6-3t=0 \iff 6=3t \iff \dfrac{6}{3}=t \iff 2=t$
Remplissage du tableau du signe :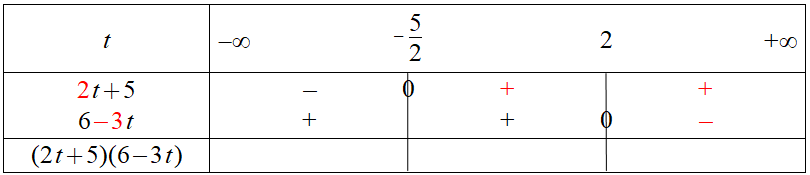
-
D'après la règle des signes en raisonnant par colonne, on obtient :
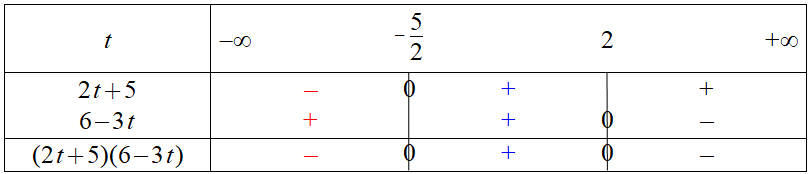
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(t)=(3t+2)(-2t-1)$.
-
Dresser le tableau de signes du produit $f(t)$.
-
Utiliser le tableau de signes pour résoudre l'inéquation $f(t)\lt 0$.
-
Utiliser Xcas pour vérifier les solutions obtenues à l'inéquation $f(t)\lt 0$.
-
Utiliser Geogebra pour vérifier les solutions obtenues à l'inéquation $f(t)\lt 0$.
Pour étudier le signe d'un quotient :
-
Commencer par chercher la valeur interdite, valeur qui annule le dénominateur,
-
Dresser le tableau de signes comme pour le produit,
-
En dernière ligne, mettre une double barre "||" en dessous de la valeur interdite.
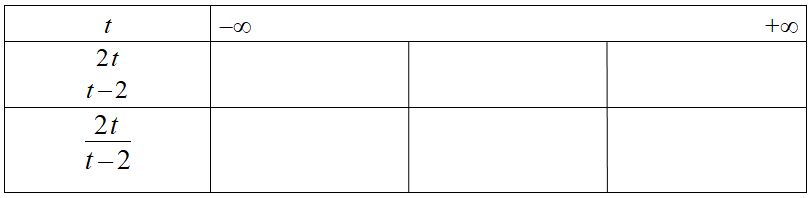
Étudier le signe du quotient $\dfrac{2t}{t-2}$.
-
Valeur interdite :
$t-2=0 \iff t=2$. 2 est la valeur interdite. (si on remplaçait $t$ par 2, on diviserait par 0) -
Tableau avec un facteur par ligne :
-
Étude du signe de chaque facteur (du numérateur) :
$2t=0 \iff t=\dfrac{0}{2} \iff t=0$
Remplissage du tableau du signe :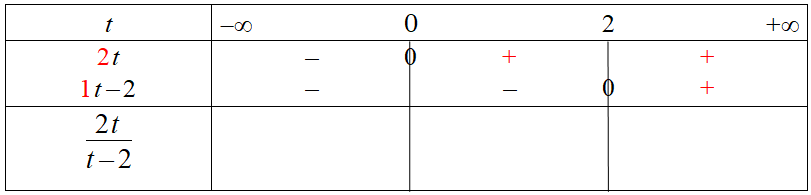
-
En mettant une double barre au niveau de la valeur interdite et en utilisant la règle des signes (en raisonnant par colonne), on obtient :
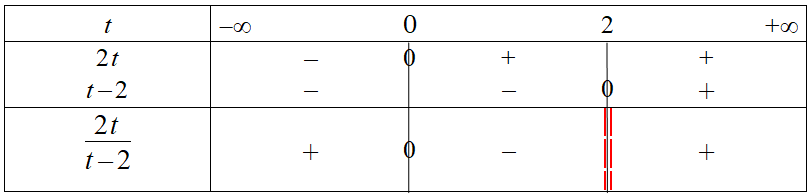
On considère la fonction $f$ définie par $f(t)=\dfrac{3-5t}{3t+5}$.
-
Dresser le tableau de signes du produit $f(t)$.
-
Utiliser le tableau de signes pour résoudre l'inéquation $f(t)\ge 0$.
-
Utiliser Xcas pour vérifier les solutions obtenues à l'inéquation $f(t)\ge 0$.
-
Utiliser Geogebra pour vérifier les solutions obtenues à l'inéquation $f(t)\ge 0$.
Exercice issu du livre scolaire.
Une voiture $V$ entre dans le parking d'une résidence au niveau du point $E$ pour se garer dans l’emplacement $E_2$
d'’'un garage (voir schéma ci-dessous).
Les 3 emplacements $E_1$, $E_2$ et $E_3$ mesurent 4 mètres chacun.
$E$ est l'entrée du parking et on note $x=EV$.
$L(x)$ est la longueur du fond du garage éclairé par les phares.
-
À quel intervalle appartient $x$ ?
-
Résolutions graphiques :
-
Tracer sur Geogebra la courbe représentant la fonction $L$.
Saisir
f(x) = Si[x ≥ 14, 21 - 0.5x,x]permet de tracer la fonction $f$ définie par $\left\{ \begin{array}{r l l} L(x) &=x &\text{si }x\text{ appartient à l'intervalle} ]-\infty;14] \\ L(x) &=21 - 0.5x & \text{si }x\text{ appartient à l'intervalle} [14;+\infty[ \end{array} \right.$ -
Lire les images de 0 et de 20 par $L$. Interpréter concrètement les valeurs lues.
-
Est-il possible que les 3 emplacements (tout le fond du garage) soient éclairés ? Justifier.
-
Préciser les valeurs de $x$ pour lesquelles l'emplacement $E$ est éclairé sur sa longueur exactement.
-
Préciser les valeurs de $x$ pour lesquelles l'emplacement $E$ est éclairé sur plus de sa longueur.
-
L’automobiliste, prudent, va rouler très doucement lorsque $E_2$ est éclairé sur moins de la moitié de sa longueur : préciser l’intervalle de $x$ correspondant.
-
-
Résolutions algébriques :
-
Dresser le tableau de signe de $40-2x$ sur $\mathbb{R}$.
-
Dresser le tableau de signe de $\dfrac{40-2x}{15-x}$ sur $\mathbb{R}$.
-
En déduire le signe de $L$ sur $[0;20]$
-
Retrouver tous les résultats du 2. par calcul.
-
On admet que la fonction $L$ est définie par $\left\{ \begin{array}{r l l} L(x) &=\dfrac{40-2x}{15-x} &\text{si }x\text{ appartient à l'intervalle} [0;14] \\ L(x) &=40-2x & \text{si }x\text{ appartient à l'intervalle} [14;20] \end{array} \right.$
Une entreprise connecte un nouveau serveur à un instant $t=0$.
On admet que la consommation de ce serveur en fonction du temps est donnée par $f(t)$, où
$f$ est la fonction définie sur $[0;+\infty[$ par $f(t)\dfrac{2t^2}{2t^2-5t+4}$, où $t$ est exprimé en minutes
et $f(t)$ est la consommation électrique en kilowatts.
-
Tracer sur Geogebra la courbe $\mathcal{C}_f$ représentant la fonction $f$.
-
Déterminer graphiquement la durée pendant laquelle la consommation électrique dépasse 2000W.
-
Vérifier sur Xcas la durée trouvée précédemment.
-
On admet que résoudre l'inéquation $f(t)\ge 2$ revient à résoudre l'inéquation $\dfrac{(t-1)(8-2t)}{2t^2-5t+4}\ge 0$.
En admettant que $2t^2-5t+4$ est toujours strictement positif, dresser le tableau de signes de $\dfrac{(t-1)(8-2t)}{2t^2-5t+4}$.
En déduire comment retrouver par calcul la durée pendant laquelle la consommation électrique dépasse 2000W. -
Déterminer par calcul la consommation électrique du serveur au bout de 2 minutes de fonctionnement.
-
Vérifier le résultat précédent sur Geogebra puis sur Xcas.
-
Déterminer les instants où la consommation électrique atteint 4kW.
Vérifier les soliutions trouvées par un calcul. -
Le chef d'entreprise espère que la consommation électrique continuera à décroître après 2 minutes de fonctionnement et que cette consommation descendra en-dessous de 1000W.
Qu'en pensez-vous ? Justifiez clairement votre réponse afin de pouvoir convaincre ce chef d'entreprise. -
On admet que la dérivée de $f$ est donnée par $f'(t)=\dfrac{(-2x)(5x-8)}{(2t^2-5t+4)^2}$.
On rappelle que le signe de cette dérivée donne les variations de $f$ :-
Sur un intervalle où $f'(t)>0$, la fonction $f$ y est strictement croissante,
-
Sur un intervalle où $f'(t)\lt 0$, la fonction $f$ y est strictement décroissante,
-
En une valeur de $t$ où $f'(t)=0$ et où $f'$ change de signe, la fonction $f$ y admet un extremum local.
Dresser le tableau de signe de $\dfrac{(-2x)(5x-8)}{(2t^2-5t+4)^2}$ puis en déduire le tableau de variations de $f$ sur $[0;+\infty[$.
-
Demander le programme !
-
Le vocabulaire sur les fonctions (antécédent, image, ensemble de définition, ...).
-
La règle des signes.
-
La règle pour connaître le signe de l'expression $at+b$.
-
Le fait qu'une valeur interdite se traduit par une double barre "||" dans un tableu de signes.
-
Calculer à la main l'image d'un réel par une fonction.
-
Calculer à la main les antécédents d'un réel par une fonction.
-
Savoir lire graphiquement les images et antécédents.
-
Savoir résoudre une inéquation simple à la main.
-
Savoir résoudre une inéquation graphiquement.
-
Savoir résoudre une équation et une inéquation grâce à Xcas.
-
Savoir résoudre une équation et une inéquation grâce à Geogebra.
-
Savoir dresser le tableau de signe d'une expression de la forme $at+b$.
-
Savoir dresser le tableau de signe d'un produit ou d'un quotient.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International