Les nombres complexes ont été introduits initialement au XVIè siècle comme "nombres imaginaires", sans réalité propre mais qui permettaient d'effectuer des calculs intermédiaires pour résoudre des équations ; le problème avait un sens réel, la conclusion avait elle aussi un sens réel mais les calculs intermédiaires ne protaient pas sur des nombres réels.
Depuis, ces nombres "imaginaires" ont gagné en sens réel : on peut calculer avec, on peut les représenter graphiquement, ils sont utiles dans pleins de domaines :
-
ces nombres permettent de modéliser l’intensité ou la tension dans des systèmes électriques ou électroniques.
-
ces nombres permettent de coder et transmettre à faible coput des fichiers audio, ...
Ces nombres s'appelent désormais nombres complexes.
Dans ce chapitre, vous allez les découvrir, apprendre à effectuer des calculs avec ces nombres et les représenter graphiquement.
Pour les plus curieux, si vous voulez découvrir une brève histoire des nombres en mathématiques avec un survol de l'apparition des nombres complexes, vous pouvez visionner en cliquant directement sur ce lien.
Définitions
Forme algébrique
On admet l’existence d’un nombre imaginaire noté $i$ tel que $i^2=-1$.
Ce nombre est souvent noté $j$ en physique pour éviter la confusion avec la notion d'intensité.
-
Tout nombre $z$ de la forme $x + yi$, où $x$ et $y$ sont deux réels, est appelé nombre complexe.
-
L’ensemble des nombres complexes est noté $\mathbb{C}$.
-
$1+2i$ est un nombre complexe avec $x=1$ et $y=2$.
-
$z=\sqrt{3}-2i$ est un nombre complexe avec $x=\sqrt{3}$ et $y=-2$.
-
$\pi$ est un nombre complexe avec $x=\pi$ et $y=0$.
-
$-5i$ est un nombre complexe avec $x=0$ et $y=-5$.
Proposer 4 autres nombres complexes.
L'écriture $x+iy$, où $x\in\mathbb{R} \textrm{ et } y\in\mathbb{R}$, d'un nombre complexe $z$ est appelée la forme algébrique du nombre complexe $z$.
Partie imaginaire et partie réelle d'un nombre complexe
Soit $z$ un complexe de forme algébrique $x+iy$.
-
Le nombre réel $x$ est appelé la partie réelle de $z$ notée $Re(z)$.
-
Le nombre réel $y$ est appelé la partie imaginaire de $z$ notée $Im(z)$.
Déterminer les parties réelle et imaginaire des complexes suivants :
- $z_1=5+2i$
- $z_2=2-8i$
- $z_3=3$
- $z_4=-2i$
- $z_5=2i+1$
-
L'ensemble des nombres réels est inclus dans l'ensemble des nombres complexes : $\mathbb{R}\subset\mathbb{C}$
-
$Re(z)$ et $Im(z)$ sont des nombres réels.
Un nombre complexe de forme algébrique $iy$ avec $y\in\mathbb{R}$ est appelé imaginaire pur.
Soient $z$ et $z'$ deux nombres complexes.
Deux complexes sont égaux si et seulement si leurs parties réelles et imaginaires sont égales.
$z=z'$ si et seulement si $Re(z)=Re(z')$ et $Im(z)=Im(z')$.
Ce théorème implique que la forme algébrique d'un nombre complexe est unique.
-
$z$ est un réel si et seulement si $Im(z)=0$.
-
$z$ est un imaginaire pur si et seulement si $Re(z)=0$.
-
$z=0$ si et seulement si $Re(z)=0$ et $Im(z)=0$.
Dans chacun des cas suivants, déterminer les réels $x$ et $y$ vérifiant l'égalité :
- $(2-x)+i(2y-3)=4+6i$.
- $(x+y)+i(2x-y-4)=0$.
Opérations sur les nombres complexes
Addition et multiplication sur les nombres complexes
$\mathbb{C}$ peut être muni ainsi d'une addition et d'une multiplication qui prolongent celles de $\mathbb{R}$ et pour lesquelles les règles de calcul restent les mêmes.
Soient deux nombres complexes $z$ et $z'$ de formes algébriques $x+iy$ et $x'+iy'$.
Pour calculer la somme de ces nombres complexes, il suffit d'additionner les deux parties réelles ensembles et les deux parties imaginaires ensemble.
$z+z'=(x+x')+i(y+y')$
soient $z=2-5i$ et $z'=-4+9i$.
$z+z'=(\color{red}{2}+\color{blue}{-5}i)+(\color{red}{-4}+\color{blue}{9}i)$ $=\color{red}{2}+\color{red}{-4}+\color{blue}{-5}i +\color{blue}{9}i$ $=\color{red}{-2}+\color{blue}{4}i$
Effectuer les additions suivantes en écrivant le résultat sous forme algébrique :
-
$z_1+z_2$ avec $z_1=5+2i$ et $z_2=-6-3i$.
-
$z_1+z_2$ avec $z_1=1-4i$ et $z_2=3+4i$.
-
$z_2+z_1$ avec $z_1=-9+5i$ et $z_2=i+7$.
-
Le nombre imaginaire $i$ est saisissable sur Xcas directement avec la lettre i :

-
Pour saisir un nombre complexe sur Xcas, penser à expliciter la multiplication entre la partie imaginaire et $i$, par exemple pour saisir $2-5i$ :

-
Xcas peut additionner deux nombres complexes, par exemple, il suffit de saisir sur Xcas : (2−5*i)+(−4+9*i) :
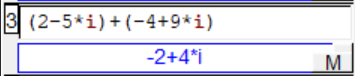
Vérifier le résultats des trois additions de l'exercice précédent à l'aide de Xcas.
Soient deux nombres complexes $z$ et $z'$ de formes algébriques $x+iy$ et $x'+iy'$.
-
Pour effectuer le produit, il suffit d'utiliser la double distributivité, puis de remplacer $i^2$ par $-1$, enfin de réduire les parties réelle et imaginaire.
On peut aboutir au résultat suivant (à ne pas apprendre par coeur, la démarche de calcul étant à refaire à chaque fois) : -
$zz'=(xx'-yy')+i(xy'+x'y)$
soient $z=2-5i$ et $z'=-4+9i$.
$z\times z'=(2-5i)\times (-4+9i)$
$=2\times (-4)+2\times 9i+ (-5i)\times(-4)+(-5i)\times (9i)$
$=-8+18i+20i-45\color{red}{i^2}$
$=-8+38i-45\times (\color{red}{-1})$
$=-8+38i+45$ $=37+38i$.
Effectuer les multiplications suivantes :
-
$(3-2i)(1+4i)$
-
$(1+\sqrt{3}i)(1-\sqrt{3}i)$
-
$(-2+5i)^2$ (penser à utiliser un produit)
Xcas peut effectuer la multiplication de deux nombres complexes à l'aide de l'opérateur $*$.
Par exemple : 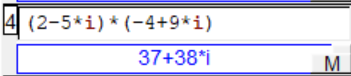
Vérifier le résultats des trois multiplications de l'exercice précédent à l'aide de Xcas.
Écrire sous forme algébrique les nombres complexes suivants (à la main puis sur Xcas) :
-
$z_1=(2+5i)+(i+3)$
-
$z_2=(3−11i)−(-8+9i)$
-
$z_3=(7+5i)(-4+3i)$
-
$z_4=(1-5i)^2$
-
$z_5=i(2-i)^2$
Conjugaison
Nombre conjugué
On appelle nombre conjugué du nombre complexe $z=x+iy$ le nombre complexe noté $\overline{z}$ de forme algébrique $x-iy$.
Donnez les conjugué des complexes suivants :
- $z_1=-5-i$
- $z_2=2-3i$
Le conjugué s'obtient sur Xcas avce l'instruction conj.
Par exemple, le conjugué de $2-5i$ est obtenu avec conj(2-5*i).
Vérifier grâce à Xcas les conjugués obtenus à l'exercice précédent.
Calculer le produit $z\times\overline{z}$ avec $z=4-3i$.
Plus généralement, on a :
Soit $z$ un nombre complexe dont la forme algébrique est $x+iy$.
$z \times \overline{z}= x^2+y^2$.
Inverse et division sur les nombres complexes
Méthode :
Pour écrire un quotient de nombres complexes sous forme algébrique, il suffit de multiplier le numérateur et
le dénominateur par le conjugué du dénominateur.
Effectuer le calcul suivant :
$\dfrac{3+2i}{1-i}$
Voici une vidéo qui reprend la méthode de la divsion de deux nombres complexes, méthode illustrée par la résolution de l'exercice précédent.
Mettre chacun des nombres complexes suivant sous forme algébrique :
-
$\dfrac{2+7i}{6-8i}$
-
$\overline{\left(\dfrac{1+2i}{3-4i}\right)}$
Vérifier sur Xcas les formes algébriques trouvées dans l'exercice précédent.
L'impédance complexe $\underline{Z}$ d'un circuit est telle que $\underline{Z}=\dfrac{\underline{Z_1}\times\underline{Z_2}}{\underline{Z_1}+\underline{Z_2}+\underline{Z_3}}$ avec $\underline{Z_1}=1+2j$, $\underline{Z_2}=-1+3j$ et $\underline{Z_3}=4+5j$ où $j$ est le nombre complexe tel que $j^2=-1$.
-
Calculer à la main l'impédance complexe $\underline{Z}$.
-
Vérifier le résultat obtenu grâce à Xcas.
À la main puis sur Xcas, déterminer la forme algébrique des nombres complexes suivant :
-
$\dfrac{1+2i}{3-i}$
-
$\dfrac{(1-i)^2}{2+2i}$
Pour une valeur fixée de la fréquence, la fonction de transfert d'un circuit a pour expression $\displaystyle{T=\dfrac{1}{\left(1+\frac{1}{2}i\right)^2}}$.
-
Calculer le nombre complexe $T$ sous forme algébrique.
-
Vérifier le résultat sur Xcas.
Résolution d'équations
Résolution d'équations du premier degré
Méthode : faire comme avec des réels en :
-
mettant tous les termes avec du $z$ dans un membre et les termes sans $z$ dans l'autre membre,
-
puis en factorisant par $z$ pour avoir une seule inconnue,
-
enfin en isolant $z$ et en mettant le résultat sous forme algébrique.
Résoudre $2z+3-i=iz-2$.
-
mettre tous les termes avec du $z$ dans un membre et les termes sans $z$ dans l'autre membre :
$2z+3-i=iz-2 \iff 2z-iz=2-3+i$
-
puis factoriser par $z$ pour avoir une seule inconnue,
$2z-iz=2-3+i \iff (2-i)z=(-1+i)$
-
enfin isoler $z$ et en mettant le résultat sous forme algébrique.
$(2-i)z=(-1+i) \iff z=\dfrac{-1+i}{2-i}$ $\iff z=\dfrac{(-1+i)(2+i)}{(2-i)(2+i)}$ $\iff z=\dfrac{-2-i+2i+i^2}{2^2+(-1)^2}$ $\iff z=\dfrac{-2+i-1}{4+1}$ $\iff z=\dfrac{-3+i}{5}$ $\iff z=-\dfrac{3}{5}+\dfrac{1}{5}i$
Conclusion : $S=\displaystyle{\left\{-\dfrac{3}{5}+\dfrac{1}{5}i\right\}}$
Résoudre l'équation suivante dans $\mathbb{C}$ : $2z+3-i=(1+i)z-5$.
L'instruction csolve(equation,inconnue) permet de résoudre une équation dans les nombres complexes.
Par exemple, pour résoudre sur Xcas l'équation $4z-3i=6-(2+i)z$, il suffit de saisir
csolve(4*z-3*i=6-(2+i)*z,z).
Résoudre sur Xcas l'équation de l'exercice précédent afin de vérifier le résultat obtenu.
Résoudre dans $\mathbb{C}$ les équations suivantes à la main puis sur Xcas :
-
$z+2i=iz−1$
-
$(2−i)z+1=(3+2i)z−i$
-
$(3+2i)(z−1)=i$
Résolution d'équation du second degré
Soit $a$ un nombre réel.
Si $a$ est non nul, l'équation $z^2=a$ admet toujours deux solutions complexes.
Plus précisément :
-
Si $a=0$, l'équation $z^2=a$ admet une unique solution complexe : 0.
-
Si $a>0$, l'équation $z^2=a$ admet deux solutions réelles : $\sqrt{a}$ et $-\sqrt{a}$.
-
Si $a<0$, l'équation $z^2=a$ admet deux solutions complexes conjuguées : $i\sqrt{|a|}$ et $-i\sqrt{|a|}$.
Résoudre dans $\mathbb{C}$ les équations suivantes :
-
$z^2+100=0$.
-
$z^2-8=0$.
-
$(2z+1)^2=25$.
Résoudre dans $\mathbb{C}$ l'équation suivante : $z^4=81$.
Le théorème suivant prolonge et précise ce que l'on a déjà vu au premier chapitre :
On considère l'équation du second degré $az^2+bz+c=0$, d'inconnue $z$, où $a$, $b$ et $c$ sont des réels avec $a\neq 0$.
Le discriminant de cette équation du second degré est $\Delta=b^2-4ac$.
-
Si $\Delta>0$, l'équation admet deux solutions réelles distinctes :$z_1=\dfrac{-b-\sqrt{\Delta}}{2a}$ et $z_2=\dfrac{-b+\sqrt{\Delta}}{2a}$.
-
Si $\Delta=0$, l'équation admet une solution réelle, dite racine double, $z_0=\dfrac{-b}{2a}$.
-
Si $\Delta<0$, l'équation admet deux solutions complexes conjuguées distinctes : $z_1=\dfrac{-b-i\sqrt{|\Delta|}}{2a}$ et $z_2=\dfrac{-b+i\sqrt{|\Delta|}}{2a}$.
-
Résoudre à la main dans $\mathbb{C}$ l'équation : $z^2-4z=-5$.
-
Résoudre à la main dans $\mathbb{C}$ l'équation : $z^2+3z+4=0$.
-
Vérifier les solutions sur Xcas.
Résoudre dans $\mathbb{C}$ les équations suivantes, d'abord à la main, puis en vérifiant sur Xcas :
-
$2z^2+32=0$
-
$z^2=3z+1$
-
$z(z+1)=-3z+5$
-
$(-z^2+3z+4)(z^2+z+1)=0$
Résoudre à la main dans $\mathbb{C}$ l'équation : $z^4+2z^2-8=0$ puis vérifier les solutions sur Xcas
Lors de la réception d'un signal émis par un satellite, il apparaît une perte d'énergie due aux
impédances de la parabole et du câble coaxial.
On mesure cette perte par le coefficient de réflexion $R$ défini par $R=\dfrac{z-z_1}{z+z_1}$, où $z$ est l'impédance complexe
de la parabole et $z_1$ celle du câble coaxial.
-
On a mesuré l'impédance complexe du câble coaxial à $4-5i$. Sachant que le coefficient de réflexion est $\dfrac{1}{2}+\dfrac{1}{2}i$, déterminer l'impédance complexe de la parabole.
-
On a mesuré l'impédance complexe du câble coaxial à $40-30i$, celle de la parabole à $50$, déterminer, par calcul, le coefficient de réflexion.
On considère un circuit comprenant une résistance, une bobine et un condensateur tels que, pour une fréquence donnée, on a : $R=10\Omega$, $L\omega=200\Omega$ et $\dfrac{1}{C\omega} =120\Omega$.
-
Déterminer les nombres complexes $\underline{Z_1}$, $\underline{Z_2}$ et $\underline{Z_3}$ correspondant aux impédances complexes de la résistance, de la bobine et du condensateur.
Rappel de physique : $\underline{Z_1}=R$, $\underline{Z_2}=jL\omega$ et $\underline{Z_3}=-\dfrac{1}{C\omega }j$, où $j$ est tel que $j^2=-1$. -
Voici un circuit électrique :
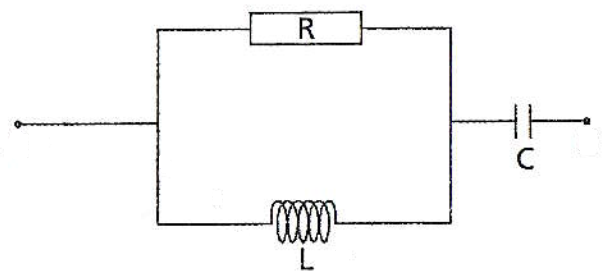
On admet que l'impédance $\underline{Z}$ complexe du circuit est donné par la formule suivante : $\underline{Z}=\underline{Z'}+\underline{Z_3}$, où $\underline{Z'}$ est le nombre complexe défini par $\dfrac{1}{\underline{Z'}} = \dfrac{1}{\underline{Z_1}} + \dfrac{1}{\underline{Z_2}}$.
-
Calculer à la main l'impédance complexe $\underline{Z}$.
-
Vérifier le résultat sur Xcas.
-
-
On considère désormais le circuit RL suivant :
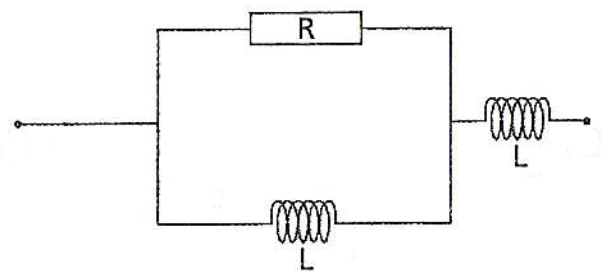
On admet que l'impédance $\underline{Z}$ complexe du circuit est donné par la formule suivante : $\underline{Z}=jL\omega+\dfrac{1}{\dfrac{1}{R}+\dfrac{1}{jL\omega}}$.
Sachant que $R=30\Omega$ et que, pour une fréquence donnée, on a $\underline{Z}=19.2+54.4j$, déterminer la valeur de $L\omega$.
Demander le programme !
-
Le vocabulaire (forme algébrique, parties réelle et imaginaires, ...),
-
la forme algébrique d'un nombre complexe,
-
$i^2=-1$,
-
la notion de conjugué d'un nombre complexe.
-
les formules donnant les solutions complexes d'une équation du second degré à coefficients réels :
-
Si $\Delta>0$, deux solutions réelles distinctes : $z_1=\dfrac{-b-\sqrt{\Delta}}{2a}$ et $z_2=\dfrac{-b+\sqrt{\Delta}}{2a}$.
-
Si $\Delta=0$, une solution : $z_0=\dfrac{-b}{2a}$.
-
Si $\Delta<0$, deux solutions complexes conjuguées distinctes : $z_1=\dfrac{-b-i\sqrt{|\Delta|}}{2a}$ et $z_2=\dfrac{-b+i\sqrt{|\Delta|}}{2a}$.
-
-
exhiber la partie réelle ou imaginaire d'un nombre complexe,
-
additioner à la main deux nombres complexes.
-
multiplier à la main deux nombres complexes.
-
conjuguer à la main un nombre complexe.
-
diviser à la main deux nombres complexes.
-
additioner sur Xcas deux nombres complexes.
-
multiplier sur Xcas deux nombres complexes.
-
conjuguer sur Xcas un nombre complexe.
-
diviser sur Xcas deux nombres complexes.
-
modéliser un problème concret dans le langage mathématique.
-
modifier la forme d'une expression grâce à Xcas.
-
résoudre une équation complexe du premier degré à la main.
-
résoudre une équation complexe du second degré (à coefficients réels) à la main.
-
résoudre une équation dans les nombres complexes grâce à Xcas.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International