Nous allons étudier dans ce chapitre la notion de suite.
Les fonctions servent à décrire et modéliser des phénomènes continus tandis que les phénomènes discrets sont modélisés
par des suites.
Ainsi, par exemple, les prêts, l’évolution des prix, des populations, les signaux numériques discrets ... sont étudiables à partir
de suites.
Définition d'une suite
Définition et notations
On considère la succession des carrés des nombres entiers naturels.
Cette succession est 0, 1, 4, 9, 16, ..., $n^2$, ...
On peut voir cette succession comme l'association suivante :
| $0\mapsto 0$ |
| $1\mapsto 1$ |
| $2\mapsto 4$ |
| $3\mapsto 9$ |
| $4\mapsto 16$ |
| ... |
| $n\mapsto n^2$ |
| ... |
Cette succession des carrés d'entiers naturels est un exemple de suite.
On appelle suite toute fonction de l’ensemble des entiers naturels $\mathbb{N}$ dans $\mathbb{R}$.
-
L’image de l'entier naturel $n$ par $u$ est appelé terme d’indice $n$ et est noté $u_n$.
-
Une suite se note $(u_n)$ ou $(u_n)_{n\in \mathbb{N}}$.
Reprenons l'exemple initial.
$u_0=0$, $u_1=1$, $u_2=4$, $u_3=9$, $u_4=16$, ..., $u_n=n^2$, ...
La suite des carrés d'entiers naturels est définie ici par $u_n=n^2$.
$u_n=n^2$ est appelé terme général de la suite $(u_n)$.
On reprend la suite précédente définie par $u_n=n^2$.
-
Calculer le sixième terme de la suite $(u_n)$.
-
Comment se note le terme suivant $u_n$ ?
-
Exprimer le terme suivant $u_n$ en fonction de $n$.
-
Comment se note le terme précédant $u_n$ ?
-
Exprimer le terme précédant $u_n$ en fonction de $n$.
Modes de génération
Une suite peut être définie par une formule explicite exprimant $u_n$ en fonction de $n$.
On considère la fonction cube $f:x \mapsto x^3$.
On définie la suite $(u_n)$ telle que pour tout entier naturel $n$, $u_n=f(n)$.
-
Calculer les 4 premiers termes de la suite $(u_n)$ des cubes d'entiers.
-
Déterminer le terme général de la suite $(u_n)$.
-
Peut-on-calculer directement le $10^{ème}$ terme de la suite $(u_n)$ ?
Soit $(u_n)$ la suite définie pour tout entier naturel $n$ par $u_n=2n^2-7n-4$.
-
La suite $(u_n)$ est peut être vue comme une suite définie par une forme explicite $u_n=f(n)$.
Déterminer l'expression de $f(x)$ permettant cette définition explicite. -
Déterminer l'expression de $u_{n+1}$ en fonction de $n$.
-
Reproduire et compléter le tableau suivant ainsi que les commentaires liés :
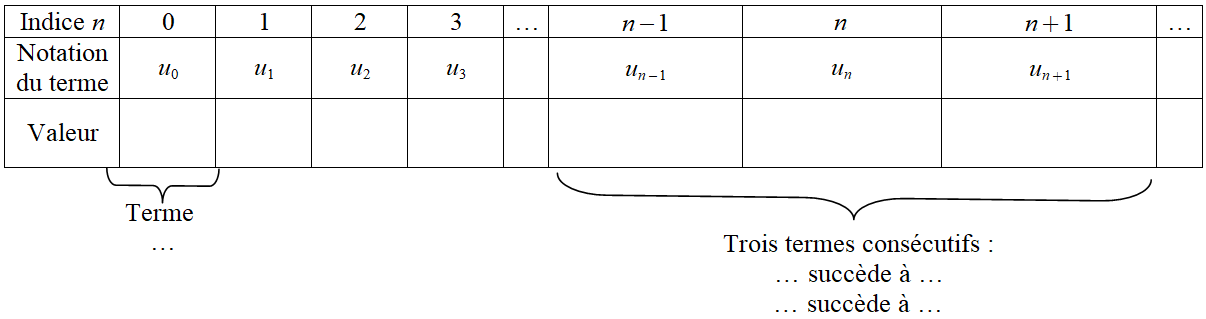
Attention à ne pas confondre :
-
$u_{n+1}$ qui est le terme succédant à $u_n$,
-
$u_n+1$ qui est le terme $u_n$ augmenté de 1.
Le respect de la position en indice est importante pour le sens donné !
Soit $(u_n)$ la suite définie par le terme général $u_n=\dfrac{2n+1}{n+2}$.
-
Calculer les 4 premiers termes de la suite des cubes d'entiers, suite notée $(u_n)$.
-
Peut-on-calculer directement le $10^{ème}$ terme de la suite $(u_n)$ ?
Une suite peut être définie par une relation de récurrence : on définit son premier terme $u_0$ et un procédé permettant, à partir de chaque terme, de calculer le terme suivant.
On considère le procédé de calcul suivant :
-
On part de 1,
-
On calcule le terme suivant en multipliant le terme précédent par 3 et en enlevant 1.
Voici les premiers termes de la suite :
-
$u_0=1$,
-
$u_1=3\times u_0-1=3\times 1-1=2$,
-
$u_2=3\times u_1-1=3\times 2-1=5$,
-
$u_3=3\times u_2-1=3\times 5-1=14$, ...
-
$u_4=3\times u_3-1=3\times 14-1=51$, ...
On peut écrire ce procédé sous la forme suivante : $\left\{ \begin{array}{l!l} u_0=&1\\[3pt] u_{n+1}=&3\times u_n -1 \text{ (pour tout entier } n \text{ de } \mathbb{N}\text{)} \end{array}\right.$
Soit $(u_n)$ la suite définie par $u_0=1$ et $u_{n+1}=u_n^2+1$ pour $n\ge 0$.
-
Calculer $u_1$.
-
Justifier que $u_2=5$.
-
Calculer les troisième et quatrième terme de la suite $(u_n)$.
-
Peut-on calculer directement le $10^{ème}$ terme de la suite $(u_n)$ ?
Soit la suite $(v_n)$ définie par $v_0=20$ et pour tout entier naturel $n$ par $v_{n+1}= \dfrac{1}{2} v_n+2$.
-
Calculer à la main les 5 premiers termes de la suite $(v_n)$.
-
Vérifier à l'aide de la calculatrice ou d'un logiciel ces premiers termes.
Utilisation du tableur de Geogebra
On peut reprend la suite suivante : $\left\{ \begin{array}{l!l} u_0=&1\\[3pt] u_{n+1}=&3\times u_n -1 \text{ (pour tout entier } n \text{ de } \mathbb{N}\text{)} \end{array}\right.$
Voici les étapes à suivre pour obtenir les premiers termes de cette suite grâce au tableur de GeoGebra :
-
Étape 1 :
Après avoir ouvert Geogebra, faire afficher le tableur en sélectionnant : Affichage --> Tableur
-
Étape 2 :
Sélectionner dans la cellule A1 la valeur du premier de la suite.
Ici saisir dans A1 le nombre 1 :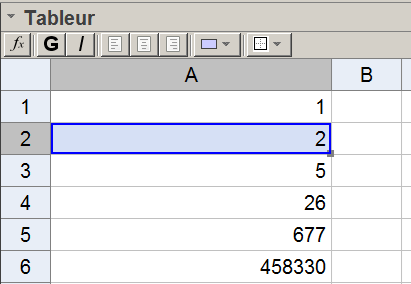
-
Étape 3:
Sélectionner dans la cellule A2 la formule $=3*A1-1$.
Cette formule découle directement de $u_{n+1}=3\times u_n -1$. -
Étape 4 :
Etape 4 : Sélectionner la cellule A2, avec le clic droit appuyé sur le carré bleu inférieur droit, faire glisser la formule jusqu'à la ligne voulue.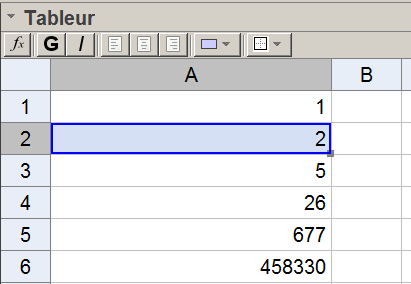
Ainsi, on en déduit que $u_5=458330$.
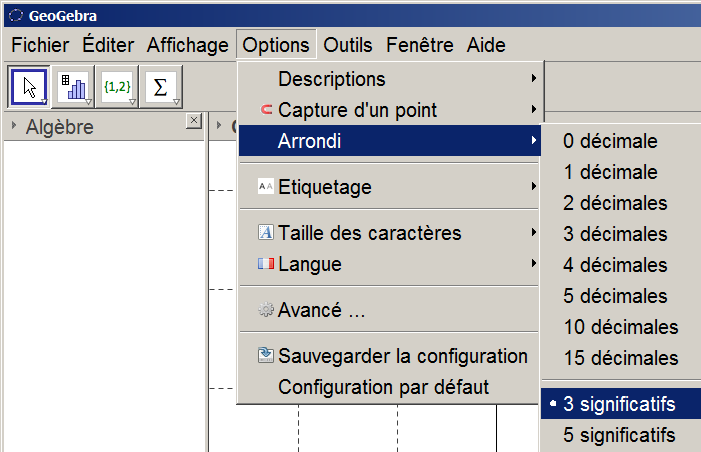
Pour avoir une valeur approchée sous écriture scientifique, il suffit de sélectionner :
Options --> Arrondi --> 3 significatifs.
On vous propose une embauche pour janvier 2025, une fois un bac+3 obtenu, avec un salaire net mensuel de 2000€.
Vous trouvez ce salaire initial en-deçà de vos attentes mais votre futur employeur vous propose
une augmentation chaque de 4% du salaire mensuel net.
Vous modélisez ce problème par une suite (car vous avez de la suite dans les idées !) :
vous notez $s_n$ le salaire mensuel en euros obtenu $n$ années après 2025.
-
Compléter la phrase suivante en précisant une opération mathématique simple :
"Augmenter de 4% revient à ... -
Utiliser le tableur de Geogebra pour créer un tableau similaire à celui présenté ci-dessous qui permet de modéliser informatiquement le problème de salaire :
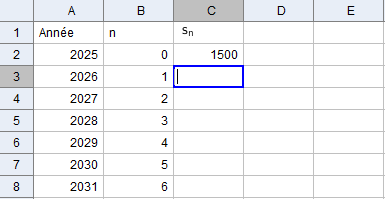
Pensez à glisser la sélection de deux cellules pour reproduire l'écart entre chaque valeur. Ainsi, vous n'aurez pas à tout saisir !
-
Quelle formule écrire dans la cellule C3 afin d'obtenir le salaire mensuel chaque année dans la colonne C ?
-
Vérifier que votre salaire en 2030 serait de 2433.31€.
-
Quel serait votre salaire en 2040 ?
-
En quelle année aurez-vous un salaire mensuel dépassant 4000€ ?
-
Vous voulez connaître votre salaire annuel dans la colonne D.
Quelle formule saisir dans la cellule D2 ? -
Vous voulez connaître votre salaire cumulé dans la colonne E, c'est-à-dire la somme de tous les salaires nets perçus depuis l'embauche en janvier 2025.
Quelle formule saisir dans la cellule E2 ? -
Supposons que vous allez travailler 42 ans dans cette entreprise. Quel serait le salaire cumulé sur l'ensemble de votre carrière dans l'entreprise
Finalement, vous vous félicitez d'avoir poursuivi vos études une année de plus : une licence pro vous permet de gagner finalement bien plus en cumulé vu les salaires proposées au niveau Bac +3 qu'avec un seul BTS !
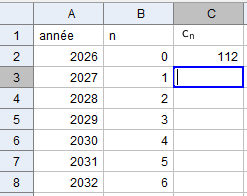
Vous reprenez en 2026 une entreprise spécialisée dans les réseaux d'entreprise. Cette entreprise a alors 112 clients
Le nombre de clients $n$ années après 2026 est noté $c_n$.
Vous projetez que la suite $(c_n)$ donnant le nombre de clients est définie par la relation de récurrence :
pour tout entier naturel $n$, $c_{n+1}=1.03\times c_n+\dfrac{n}{4}$.
-
Recopier le tableau suivant sur un tableur :
-
Quelle formule saisir dans la cellule C3 afin d'obtenir dans la colonne C les valeurs successives de la suite $(c_n)$ sachant que, pour tout entier naturel $n$, $c_{n+1}=1.03\times c_n+n/4$ .
-
Vérifier qu'en 2028, votre entreprise possèdera 119 clients.
-
Combien d'années seront nécessaires pour que votre nombre de clients soit au moins doublé ?
Utilisation d'un algorithme pour calculer les premiers termes
Recopier et compléter l'algorithme ci-dessous en pseudo-langage afin qu'ils permettent de connaître la valeur du terme d'indice 20 de la suite définie par $u_0=10$ et pour tout entier $n$ : $u_{n+1}=\dfrac{5u_n+1}{2u_n+n}$.
n ← ...
u ← ...
Pour ... allant de ... à ... faire
... ← ...
... ← ...
Fin_Pour
Afficher("Le terme d'indice 20 est ", ...)
Recopier et compléter l'algorithme ci-dessous en pseudo-langage afin qu'ils permettent de connaître la valeur du terme d'indice 20 de la suite définie par $u_0=10$ et pour tout entier $n$ : $u_{n+1}=\dfrac{5u_n+1}{2u_n+n}$.
n ← ...
u ← ...
Tant que ... faire
... ← ...
... ← ...
Fin_Tant que
Afficher("Le terme d'indice 20 est ", ...)
Soit la suite $(v_n)$ définie par $v_0=20$ et pour tout entier naturel $n$ par $v_{n+1}= \dfrac{1}{2} v_n+2$.
Proposer un algorithme qui permet d'obtenir les $p$ premiers termes de la suite où $p$ est choisi par l'utilisateur.
Suites arithmétiques
Exemple d’introduction : placement "avec intérêt simple"
Une banque propose, pour un placement d’un montant de 1500 euros fait le 1er janvier 2020, un taux d’intérêt simple
annuel de 2 %. Cela signifie qu’à la fin de chaque année on reçoit un intérêt représentant 2% du capital initial
versé le 1er janvier 2022. Ce capital est noté $C_0$.
Le capital disponible au bout d’un an est noté $C_1$ et le capital disponible au bout de 2 ans $C_2$, ...
le capital disponible au bout de $n$ ans est noté $C_n$.
-
Justifier que $C_1=1530$ et que $C_2=1560$.
-
Calculer $C_3$.
-
Établir une relation entre $C_n$ et $C_{n+1}$ en utilisant le fait qu'une seule année sépare ces deux montants du capital.
-
Déterminer la relation permettant de connaître $C_n$ à partir de $C_0$ et de $n$.
-
Si on laisse pendant 10 ans le compte sans retirer d’argent alors combien y aura-t-il au bout de dix ans ?
Définition et formules
Une suite arithmétique est une suite dans laquelle chaque terme sauf le premier est obtenu en ajoutant un réel constant $r$, appelé raison, au terme précédent.
Toute suite arithmétique peut être définie :
-
par une formule de récurrence :
Pour tout entier naturel $n$, $u_{n+1}=u_n+r$, avec comme premier terme $u_0$.
-
par une formule explicite :
Pour tout entier naturel $n$, $u_n=u_0+r\times n$.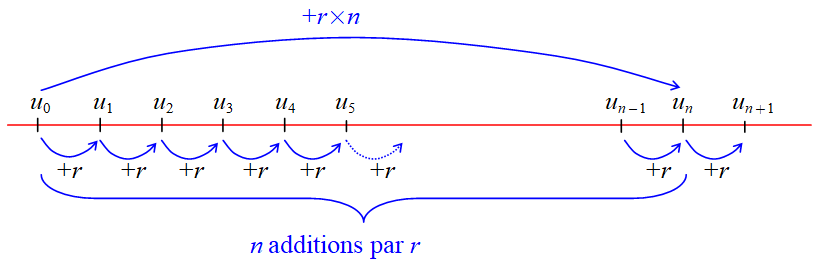
La suite de l'exemple précédent a :
-
pour formule de récurrence : pour tout entier naturel $n$, $u_{n+1}=u_n+30$, avec comme premier terme $u_0=1500$.
-
pour formule explicite : pour tout entier naturel $n$, $u_n=1500+30n$.
On considère $(u_n)$ une suite arithmétique de premier terme $u_0$ et de raison $r$.
On admet que $u_0=-3$ et $u_{14}=25$.
Utiliser les deux formules précédentes afin de répondre aux deux questions suivantes.
-
Calculer la raison $r$ de cette suite arithmétique.
-
Calculer le terme $u_{13}$.
Sens de variation
Une suite arithmétique est :
-
strictement croissante si $r>0$,
-
strictement décroissante si $r\lt 0$,
-
constante si $r=0$.
On considère une suite arithmétique $(u_n)$.
Déterminer l'expression du terme général $u_n$ en fonction de $n$ et les variations de la suite $(u_n)$
dans chacun des cas suivants :
-
Le premier terme est 1000 et la raison est -150.
-
Le premier terme est 2 et la raison est 3.
Suites géométriques
Exemple d’introduction : placement "avec intérêt composé"
Une banque propose, pour un placement d’un montant de 1500 euros fait le 1er janvier 2020, un taux d’intérêt composé
annuel de 2 %. Cela signifie qu’à la fin de chaque année on reçoit un intérêt représentant 2% du capital présent sur
le compte en début d'année. Le capital initial est noté $C_0$.
Le capital disponible au bout d’un an est noté $C_1$ et le capital disponible au bout de 2 ans $C_2$, ...
le capital disponible au bout de $n$ ans est noté $C_n$.
-
Justifier que $C_1=1530$ et que $C_2=1560,60$.
-
Calculer $C_3$.
-
Établir une relation entre $C_n$ et $C_{n+1}$ en utilisant le fait qu'une seule année sépare ces deux montants du capital.
-
Déterminer la relation permettant de connaître $C_n$ à partir de $C_0$ et de $n$.
-
Si on laisse pendant 10 ans le compte sans retirer d’argent alors combien y aura-t-il au bout de dix ans ?
Définition et formules
Une suite géométrique est une suite dans laquelle chaque terme sauf le premier est obtenu en multipliant un réel constant $q$, appelé raison, au terme précédent.
Toute suite géométrique peut être définie :
-
par une formule de récurrence :
Pour tout entier naturel $n$, $u_{n+1}=u_n\times q$, avec comme premier terme $u_0$.
-
par une formule explicite :
Pour tout entier naturel $n$, $u_n=u_0\times q^n$.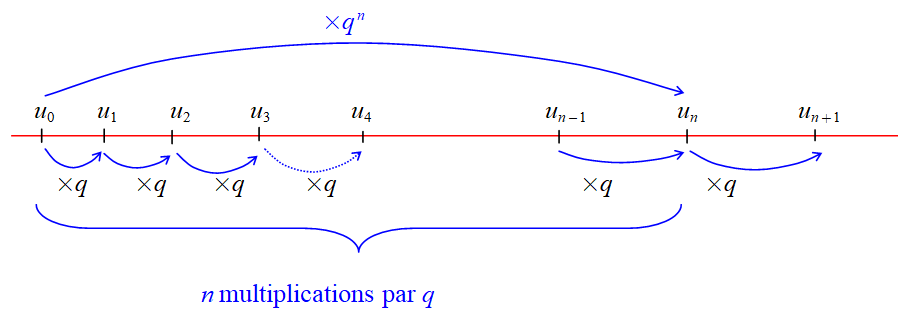
On considère $(u_n)$ une suite géométrique de premier terme $u_0$ et de raison $q$.
On admet que $u_4=6$ et $u_7=48$.
Utiliser les deux formules précédentes afin de répondre aux deux questions suivantes.
-
Calculer la raison $q$ de cette suite géométrique.
-
Calculer le terme $u_5$.
Sens de variation
L’accroissement $u_{n+1}-u_n$ entre deux termes consécutifs d’une suite géométrique de raison $q$ vaut $u_n \times (q-1)$.
Une suite géométrique à termes postifs est :
-
strictement croissante si $q>1$,
-
strictement décroissante si $0\lt q\lt 1$,
-
constante si $q=1$.
On considère une suite arithmétique $(u_n)$.
Déterminer l'expression du terme général $u_n$ en fonction de $n$ et les variations de la suite $(u_n)$
dans chacun des cas suivants :
-
Le premier terme est 1000 et la raison est $\dfrac{1}{2}$.
-
Le premier terme est 2 et la raison est 3.
Limites d'une suite géométrique
Dans un certain type de fibre optique, la qualité d'une information numérique est réduite de 1% pour chaque
kilomètre de fibre parcouru.
On note $q_n$ la qualité de l'information à $n$ kilomètres de fibre parcouru. On prend comme valeur de départ $q_0=1$.
-
Quelle est la nature de la suite $(q_n)$ ?
-
Quelles variations pour la suite $(q_n)$ conjecturez-vous ?
-
Proposez une démarche permettant de vérifier cette conjecture.
-
Que penser de la qualité du signal au bout d'un grand nombre de kilomètres parcourus ?
-
On veut vérifier la conjecture du 4. à l'aide d'un algorithme.
Pour cela, on cherche à savoir au bout de combien de kilomètresnla qualité du signalqdevient inférieur à la précisionpque choisi l'utilisateur du programme.
Compléter l'algorithme suivant pour vérifier la conjecture du 4.... p n ← ... q ← ... ... faire ... ← ... ... ← ... Fin_... Afficher("Le signal devient trop atténué au bout du kilomètre", ...)
Ce théorème sur les limites d'une suite géométrique est non exigible au CCF
Soit $(u_n)$ une suite géométrique définie par $u_0\times q^n$.
-
Si $-1\lt q\lt 1$ alors la suite $(u_n)$ converge vers 0 : $\displaystyle \lim_{n \rightarrow +\infty} u_n = 0$.
-
Si $q=1$ alors la suite $(u_n)$ est constante à $u_0$ et converge donc vers $u_0$ : $\displaystyle \lim_{n \rightarrow +\infty} u_n = u_0$.
-
Si $q>1$ alors la suite $(u_n)$ diverge vers l'infini :
-
Si $u_0>0$ alors $\displaystyle \lim_{n \rightarrow +\infty} u_n = +\infty$.
-
Si $u_0\lt 0$ alors $\displaystyle \lim_{n \rightarrow +\infty} u_n = -\infty$.
-
-
Si $q\le -1$ alors la suite $(u_n)$ diverge.
Comparaisons de suites arithmétiques et géométriques
Ces deux suites ont deux représnetations graphiques distinctes et remarquables :
-
Si $u(u_n)$ est une suite arithmétique :
Dans un repère $(O ; \overrightarrow{i}, \overrightarrow{j})$, on considère $M_n$ le point d’abscisse $n$ et d’ordonnée $u_n=u_0+n\times r$.
Tous les points $M_n$ sont alignés sur la droite d’équation $y=r\times x+u_0$. -
Si $u(u_n)$ est une suite géométrique :
Dans un repère $(O ; \overrightarrow{i}, \overrightarrow{j})$, on considère $M_n$ le point d’abscisse $n$ et d’ordonnée $u_n=u_0\times q^n$, avec $q>0$.
Tous les points $M_n$ appartiennent à une courbe exponentielle car pour tout entier naturel $n$ $u_n=u_0\times e^{n\times \ln(q)}$.
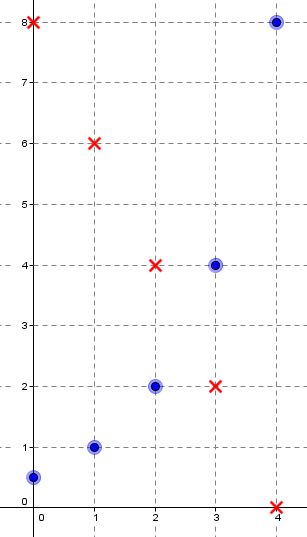
Déterminer la nature ainsi que l’expression des deux suites représentées ci-dessous.
La suite $(u_n)$ est représentée par les croix rouges tandis que la suite $(v_n)$ est représentée par les
points bleus.
Exercices
Calcul de termes
Soit la suite $(u_n)$ définie pour tout entier naturel $n$ par $u_n= \dfrac{n^2-2n}{n+1}$.
-
Calculer à la main les 5 premiers termes de la suite $(u_n)$.
-
Vérifier à l'aide de la calculatrice ou d'un logiciel ces premiers termes.
Soit la suite $(u_n)$ définie pour tout entier naturel $n$ par $u_n= n^2-n+2$.
-
Calculer à la main les 5 premiers termes de la suite $(u_n)$.
-
Vérifier à l'aide de la calculatrice ou d'un logiciel ces premiers termes.
-
Déterminer l'expression de $u_{n+1}$ en fonction de $n$.
Soit la suite $(u_n)$ définie par $u_{0}=20$ et, pour tout entier naturel $n$, $u_{n+1}= \dfrac{1}{2}u_n+2$.
-
Calculer à la main les 5 premiers termes de la suite $(u_n)$.
-
Vérifier à l'aide de la calculatrice ou d'un logiciel ces premiers termes.
Algorithme
Soit la suite $(u_n)$ définie par $u_{0}=20$ et, pour tout entier naturel $n$, $u_{n+1}= \dfrac{1}{2}u_n+2$.
Proposer un algorithme qui permet d'obtenir les $p$ premiers termes de la suite où $p$ est choisi par l'utilisateur.
Soit la suite $(u_n)$ est une suite arithmétique de premier terme -2.5 et de raison $r=4.5$.
-
Exprimer le terme général $u_n$ en fonction de $n$.
-
On considère l'algorithme ci-dessous :
S ← 0 Pour n allant de 0 à 2 faire u ← -2.5+4.5*n S ← S+u Afficher S Fin_Pour
Recopier et compléter le tableau suivant en mettant en œuvre l'algorithme :
$n$ $u_n$ $S$ 0 ... ... 1 ... ... 2 ... ... 3 ... ... -
Que permet cet algorithme ?
-
Que se passe-t-il si les deux dernières lignes de l'algorithme sont premutées de sorte que l'algorithme devienne :
S ← 0 Pour n allant de 0 à 2 faire u ← -2.5+4.5*n S ← S+u Fin_Pour Afficher S
Soit la suite $(u_n)$ est une suite définie par $u_0=2$ et pour tout entier naturel $n$ par $u_{n+1}=\dfrac{1}{2}u_n+n-1$.
-
Calculer à la main les premières valeurs $u_1$, $u_2$ et $u_3$.
-
Recopier et compléter l'algorithme suivant afin qu'il calcule et affiche le terme de rang 100 :
u ← ... n ← ... Pour i allant de ... à ... faire ... ← ... ... ← ... ... Fin_Pour ...
-
Comment modifier l'algorithme afin qu'il affiche les 101 premiers termes ?
-
On désire vérifier les résultats obtenus grâce à l'algorithme à l'aide du tableur. On a déjà commencer à remplir certaines cases d'un tableur comme le montre cette image :

Quelle formule saisir dans la cellule B3 afin que par glissement, on puisse obtenir la succesion des valeurs prises par la suite $(u_n)$ dans la colonne B ?
-
Modifier l'algorithme afin qu'il calcule et affiche aussi la somme de tous les termes entre $u_0$ et $u_{100}$.
Pour cela, vous pouvez utiliser une nouvelle variable $S$. -
Quelles formules suffit-il de saisir dans la cellule C2 et C3 afin d'obtenir, par glissement, dans la colonne C la somme de tous les termes de la suite entre $u_0$ et $u_{n}$ ?
Problèmes concrets
Une personne a placé, le 1er janvier 2022, 5000€ à intérêts composés au taux annuel de 1.5%.
On note $C_n$ le capital de cette personne au bout de $n$ années de placement.
-
Déterminer la nature de la suite $(C_n)$ en justifiant d'une phrase. (arithmétique, géométrique, ...)
-
Déterminer l'expression de $C_n$ en fonction de $n$.
-
Compléter l'algorithme suivant permettant de savoir au bout de combien d'années le capital aura doublé.
n ← ... C ← ... ... faire ... ← ... ... ← ... Fin_Pour Afficher ...
Une mairie a étudié l'évolution de la population de cette ville : chaque année, 4% de sa population de la ville la quitte
mais 200 personnes s'y installent. En 2022, il y a 10000 habitants dans cette ville.
On note $u_n$ la population de la ville l'année $2022+n$.
-
Que vaut $u_0$ ?
-
Calculer $u_1$ et $u_2$.
-
Déterminer la relation de récurrence entre $u_{n+1}$ et $u_n$.
-
Utiliser la calculatrice ou un logiciel pour obtenir les premiers termes de la suite.
-
Quelles semblent être les variations de la suite $(u_n)$ ?
-
Proposer un algorithme qui permet de connaître la population de la ville en 2050.
-
Proposer un algorithme qui permet de savoir en quelle année la population de la ville sera inférieure à 5200 habitants.
Vous gagné 1000€. Vous décidez de les placer à la banque. Elle vous propose de gagner 2% chaque année sur la somme présente sur le compte l'année d'avant. On note $u_n$ la somme d'argent possédée au bout de $n$ années de placement sans retrait.
-
Quelle est la nature de la suite $(u_n)$ ? Justifier d'une phrase.
-
Déterminer le nombre d'années nécessaire pour doubler votre capital initial.
Vous désirez acheter un local en centre ville pour votre entreprise de services informatiques pour les particuliers
et les entreprises.
Pour cela, vous devez recourir à un emprunt de 100000€ auprès d'une banque.
Vous vous adressez à deux banques appellée "Banque Al" et "Banque Yeah !".
La banque "Banque Al" vous propose de rembourser le prêt sur 7 années. Chaque année vous aurez à verser annuellement
une somme d'argent augmentant linéairement. La première année vous aurez à rembourser 15000€. Chaque année, vous aurez
à rembourser en plus de la somme versée l'année précédente 1800€.
On note $u_n$ le remboursement à verser à cette banque "Banque Al" $n$ années après le premier remboursement.
La banque "Banque Yeah !" vous propose aussi de rembourser le prêt sur 7 années. Chaque année vous aurez à verser annuellement
une somme d'argent augmentant régulièrement La première année vous aurez à rembourser 20000€. Chaque année, la somme
à rembourser augmente de 2% par rapport à l'année précédente.
On note $v_n$ le remboursement à verser à cette banque "Banque Yeah!" $n$ années après le premier remboursement.
-
-
Que vaut $u_0$ ? $u_1$ ? $u_2$ ?
-
Quel est le montant du dernier versement ?
-
Quelle somme aurez-vous en tout rembourser à la banque "Banque Al" si vous décidez de souscrire le prêt chez elle ?
-
Quel serait le coût sur 7 ans de ce prêt ?
-
-
-
Que vaut $v_0$ ? $v_1$ ? $v_2$ ?
-
Quel est le montant du dernier versement ?
-
Quelle somme aurez-vous en tout rembourser à la banque "Banque Yeah !" si vous décidez de souscrire le prêt chez elle ?
-
Quel serait le coût sur 7 ans de ce prêt ?
-
-
Quelle banque vous offre la solution la plus avantageuse ?
L’accès internet chez les particuliers peut se faire encore aujourd’hui en ADSL.
Cette liaison utilise les câbles téléphoniques pour relier le particulier au DSLAM
(répartiteur du fournisseur d’accès choisi). La puissance du signal dépend de l’atténuation engendrée par les
longueurs de câbles téléphoniques, la puissance du signal diminue de 29.2 % par tronçon de 100 mètres de câbles.
-
-
Exprimer la puissance $P_1$ disponible après un tronçon de 100 mètres de câble en fonction de $P_1$.
-
Vérifier que la proportion de puissance disponible après 2 tronçons de câbles de 100 mètres est égale à 50.1% (valeur arrondie à 0.1 près).
-
Déterminer la valeur arrondie à 0.1 près de la proportion de puissance disponible après 5 tronçons de câble de 100 mètres.
-
-
On note $P_n$ la puissance à la sortie de $n$ tronçons de câbles de 100 mètres, $n$ étant un entier naturel.
-
Quelle est la nature de la suite $(P_n)$ ? Justifier.
-
Pour tout entier naturel $n$, exprimer $P_n$ en fonction de $n$ et de $P_0$.
-
En déduire la proportion de puissance disponible après 15 tronçons de 100 mètres.
-
-
On admet que pour tout entier naturel $n$, la suite $(P_n)$ est définie par : $P_n=P_0\times 0.708^n$.
-
Quelle est la limite de la suite $(P_n)$ ?
-
Justifier qu’il existe un entier naturel $N$ tel que, pour tout entier $n$ supérieur à $N$, on ait : $0.708^n\le 10^{-7}$.
-
En utilisant un outil informatique, déterminer la plus petit entier $N$ tel que $0.708^N\le 10^{-7}$.
-
Retrouver la réponse par un calcul algébrique.
-
La limite d’éligibilité au service ADSL est telle que : $\dfrac{P_S}{P_E}=1\times 10^{-7}$, où $P_S$ désigne la puissance du signal chez le particulier et $P_E$ la puissance fourni par le DSLAM.
Déterminer la distance théorique maximale de câblage entre le particulier et le DSLAM qui permette le fonctionnement de l’ADSL chez le particulier. (On donnera la valeur arrondie au mètre près.)
-
On appelle $P_0$ la puissance disponible au répartiteur (DSLAM).
On dispose d'un crédit de 414000€ pour atteindre dans le désert une nappe souterraine.
Le coût du forage est fixé à 1000€ pour le premier mètre creusé, 1200 pour le deuxième, 1400 pour le troisième
et ainsi de suite en augmentant de 200€ par mètre creusé.
On note $u_n$ désigne donc le coût en euros du $(n+1)$ième mètre creusé.
-
-
Calculer $u_5$.
-
Exprimer $u_{n+1}$ en fonction de $u_n$, pour tout entier naturel $n$.
-
En déduire la nature de la suite $(u_n)$.
-
Exprimer $u_n$ en fonction de $n$, pour tout entier naturel $n$.
-
-
Pour tout entier naturel non nul $n$, on désigne par $S_n$ le coût total en euros d'un puits de $n$ mètres.
Par exemple le coût total d'un puits de 3 mètres est $S_3=u_0+u_1+u_2$.
Proposer un algorithme qui permette de savoir quelle profondeur on peut atteindre avec un crédit de 414000€. -
On admet que pour tout entier naturel $n$ non nul $S-n=100n^2+900n$.
Retrouver la profondeur maximale que l'on peut atteindre avec le crédit de 414000€.
Un ordinateur a été initialement mis sur le marché au prix de 1000€.
Du fait des progrès techniques, le prix de vente de ce modèle d'ordinateur diminue de 3% chaque mois.
Déterminer le nombre de trimestre nécessaire pour que le prix de vente devienne inférieur à 200€.
Dans un certain type de fibre optique, la puissance du signal transmettant une information numérique est réduite de 2% pour chaque kilomètre de fibre parcouru.
-
Quelle pourcentage de la puissance initiale reste-t-il au bout de 10 kilomètres ?
-
Il est nécessaire d'amplifier le signal lorsque sa puissance descend en-dessous de 20% de celle initiale.
À quelle distance doit-on installer un amplificateur ?
Vous gagnez à un jeu 10000€.
Vous décidez de placer cette somme en banque. Celle-ci vous propose deux contrats :
-
le premier : chaque année le capital augmente de 250€.
-
le second : chaque année le capital augmente de 2%.
Pour un placement sur 10 ans, quel est le placement le plus intéressant ?
Au 1er janvier 2022, un particulier installe 20 $m^2$ de panneaux photovoltaïques à son domicile.
Pour estimer la rentabilité de cette installation, il utilise la documentation suivante :
|
En France, 1 $m^2$ de panneaux photovoltaïques correctement orientés produit environ 95 kWh/an. |
|---|
Pour tout entier $n\ge 0$, on note $u_n$ la quantité d’énergie produite par l’installation durant l’année $2022+n$.
-
Déterminer la production énergétique en 2022 puis en 2023.
-
En quelle année, la quantité d'énergie produite deviendra-t'elle inférieure à 150 kWh/an ?
-
Proposer une démarche qui permet de savoir le nombre d'années nécessaires pour assurer la rentabilité financière.
-
La durée de vie d'une telle installation est estimée à 20 ans. L'installation est-elle rentable ?
Demander le programme !
-
Savoir les formules sur les suites arithmétiques ($u_{n+1}=u_n+r$, $u_n=u_0+n\times r$)
-
Savoir les formules sur les suites géométriques ($u_{n+1}=q\times u_n$, $u_n=u_0\times q^n$)
-
Savoir le sens de variations des suites arithmétiques et géométriques.
-
Savoir calculer des termes d'une suite définie par une formule explicite.
-
Savoir calculer les premiers termes d'une suite définie par une formule de récurrence.
-
Savoir utiliser un tableur pour calculer les premiers termes d'une suite.
-
Savoir utiliser un tableur pour obtenir l'indice de la première valeur d'une suite dépassant un seuil donné.
-
Savoir écrire ou compléter un algorithme pour obtenir des termes d'une suite.
-
Savoir écrire ou compléter un algorithme pour obtenir la somme de termes d'une suite.
-
Savoir écrire ou compléter un algorithme pour obtenir l'indice de la première valeur d'une suite dépassant un seuil donné.
-
Savoir utiliser un coefficient multiplicateur pour modéliser une variation en pourcentage.
-
Savoir modéliser un problème concret à l'aide d'une suite.
-
Savoir comparer deux suites.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International