Intérêt
De nombreuses situations en électricité, en mécanique ou en économie se traduisent par des équations différentielles,
comme par exemple l'étude de la stabilité, d'oscillations, de l'amortissement, des fréquences propres,
des phénomènes de résonance, ...
Définitions
Une équation différentielle est une équation dont l’inconnue n’est pas un nombre, mais une fonction $f$ et dans laquelle apparaît au moins une dérivée de $f$.
Voici quelques exemples d'équations différentielles :
-
$f'(t)=f(t)$ est une équation différentielle, d'inconnue $f$.
Une solution ce dette équation est la fonction exponentielle $f:t\mapsto\exp(t)$. -
$t\times f'(t)-2f(t)=t^3 \times e^t$.
Ici, $f$ est la fonction inconnue, fonction dépend de la variable $t$.
Notation
Par convention, on note l'inconnue souvent $y$ au lieu de $f$.
Ainsi, l'équation différentielle $f'(t)=f(t)$ est plutôt notée $y'=y$.
Lorsque seule la dérivée intervient dans l’équation, c’est une équation différentielle du $1^{\text{er}}$ ordre.
-
$y'-3y=4t^2+5$ est une équation différentielle du premier ordre.
-
$y''-3y'+2y=t+4$ n'est pas une équation différentielle du premier ordre car la dérivée seconde $y''$ apparaît dans cette équation.
En physique, on peut utiliser les notations différentielles afin d’écrire ces équations différentielles.
Par exemple, dans un circuit RL soumis à une tension variable $u(t)$, l’intensité $i$ du courant vérifie l’équation différentielle : $Li'(t)+Ri(t)=u(t)$, ce qui se note $L \dfrac{di}{dt}(t)+Ri(t)=u(t)$.
Bon, maintenant que vous êtes au courant des définitions et des notations, passons aux formules ! Hein ?
Résolution d'équations différentielles du premier ordre
Équation différentielle homogène
Une équation différentielle pouvant s'écrire sous la forme $ay'(t)+by(t)=0$ est appelée une
équation différentielle homogène du premier ordre à coefficients constants.
Les coefficients $a$ et $b$ sont deux réels.
homogène signifie qu'aucun autre terme que ceux liés à $y'$ et $y$ n'apparaissent dans l'équation.
Voici sur Geogebra, la courbe obtenue comme représentation de la solution de l'équation différentielle $y'-2y=0$ avec $y$ une fonction définie et dérivable sur $\mathbb{R}$ vérifiant de plus $y(t_0)=y_0$ où $t_0=2$ et $y_0=1$.
Dans le logiciel GeoGebra, l’instruction (tapée dans la ligne « Saisie »)
RésolEquaDiff[2*y,t_0,y_0,10,0.01] permet de tracer la représentation graphique de la solution de
$y'-2y=0$ avec $y$ vérifiant de plus $y(t)=y_0$ où $t_0=2$ et $y_0=1$, lorsque les curseurs t_0 et y_0
prennent respectivement les valeurs 2 et 1.
La quatrième argument, 10, correspond à l'abscisse maximale de $x$ pour laquelle on souhaite tracer la courbe représentative
de la solution cherchée.
Le dernier argument, 0.01, correspond au pas de calcul utilisé pour obtenir une solution approchée de la solution réelle.
Ce code permet de tracer la courbe représentative approchée entre t_0 et 10.
Le code h = RésolEquaDiff[2y, t_0, y_0, -10, -0.01]permet similairement
de tracer la courbe représentative approchée entre t_0 et 10.
-
Lorsque les curseurs
t_0ety_0prennent respectivement les valeurs 2 et 1, combien de fonction solution admet l'équation différentielle au vu des tracés ? -
À quelle fonction de référence vous fait penser l'allure du tracé obtenu pour la solution ?
-
Faites varier les curseurs
t_0ety_0.
Que remarquez-vous quant au nombre de solution et à l'allure générale de la courbe obtenue ?
-
Si $a$ et $b$ sont deux constantes réelles, la solution générale de l’équation différentielle homogène $ay'(t)+by(t)=0$ est l’ensemble des fonctions $y$ définies sur $\mathbb{R}$ par $y(t)=ke^{-\frac{b}{a}t}$, où $k$ est une constante réelle.
-
Dès que l'on impose en plus une condition initiale du type $y(t_0)=y_0$, alors l'équation différentielle homogène $ay'(t)+by(t)=0$ admet une unique solution $y$ définie sur $\mathbb{R}$ par $y(t)=ke^{-\frac{b}{a}t}$, où $k$ est tel que $ke^{-\frac{b}{a}t_0}=y_0$.
La forme de l'ensemble des solutions de l’équation différentielle homogène $ay'(t)+by(t)=0$ s'appelle la solution générale de l’équation différentielle $ay'(t)+by(t)=0$.
On considère l'équation différentielle $2y'+3y=0$.
-
La fonction $f:t\mapsto 5e^{-\frac{3}{2}t}$ est une fonction solution ; ici $k=5$.
-
La fonction $f:t\mapsto \dfrac{\pi}{4}e^{-\frac{3}{2}t}$ est une autre fonction solution ; ici $k=\dfrac{\pi}{4}$.
-
Toutes les fonctions solutions de l'équation différentielle sont de la forme $y(t)=ke^{-\frac{b}{a}t}$, avec $k$ est une constante réelle.
-
L'équation différentielle $2y'+3y=0$ admet une unique solution $f$ telle que $f(1)=4$, c'est la fonction $f:t\mapsto 4e^{-\frac{3}{2}}\times e^{-\frac{3}{2}t}$ car avec cette valeur $k=4e^{-\frac{3}{2}}$, on a bien : $f(1)=4$
Pour résoudre trouver la solution d'une équation homogène (E) $ay'(t)+by(t)=0$ vérifiant une certaine condition $y(t_0)=y_0$, il suffit :
-
Étape 1 :
Trouver toutes les solutions de l'équation homogène (E) $ay'(t)+by(t)=0$ en utilisant la formule du cours $y(t)=ke^{-\frac{b}{a}t}$ avec $k\in \mathbb{R}$. -
Étape 2 :
Remplacer $y(t)$ par son expression et résoudre l'équation $y(t_0)=y_0$, d'inconnue $k$, pour trouver la seule fonction solution de l'équation différentielle (E) vérifiant en plus $y(t_0)=y_0$.
Pour de déterminer $k$, il suffit de résoudre sur Xcas l'équation du type $y(t_0)=y_0$ en spécifiant $k$ comme inconnue.
On considère dans cet exercice l'équation différentielle (E) $y'(t)+2y(t)=0$.
-
Déterminer à la main l'ensemble des fonctions solutions de l'équation différentielle (E).
-
Déterminer à la main la solution $f$ de l'équation différentielle (E) telle que $f(3)=-5$.
Résoudre l'équation différentielle $(E_0)$ $2y'(t)-3y(t)=0$ sur $\mathbb{R}$ avec $y(1)=2$.
Résolution sur Xcas
La fonction desolve(equation, inconnue) permet de résoudre sur Xcas des équations différentielles.
Plus précisément :
-
Pour résoudre une équation différentielle homogène $ay'(t)+by(t)=0$, il suffit de saisir sur Xcas :
desolve(a*y'+b*y=0,y). -
Pour résoudre une équation différentielle homogène $ay'(t)+by(t)=0$ avec une condition du type $y(t0)=y0$, il suffit de saisir sur Xcas :
desolve([a*y'+b*y=0,y(t0)=y0],y).
Attention !
Sur Xcas, la variable de la fonction inconnue y est par défaut x.
Ne pas oublier les crochets pour lier une équation différentielle avec sa condition initiale.
desolve pour differential equation + solve.
Le but est de rétrouver grâce à Xcas, les solutions des équations différentielles trouvées lors de l'exercice 2.
-
Déterminer sur Xcas l'ensemble des fonctions solutions de l'équation différentielle (E) $y'(t)+2y(t)=0$.
-
Déterminer sur Xcas la solution $f$ de l'équation différentielle (E) $y'(t)+2y(t)=0$ telle que $f(3)=-5$.
Équation différentielle avec second membre
On appelle équation différentielle du premier ordre avec second membre toute équation différentielle pouvant s'écrire sous la forme $ay'(t)+by(t)=c(t)$, où $a$ est un réel non nul, $b$ est un réel quelconque et $t\mapsto c(t)$ est une fonction définie sur $\mathbb{R}$.
Soient $a$ et $b$ deux réels avec $a\neq 0$.
L'ensemble des solutions de l’équation différentielle $ay'(t)+by(t)=c(t)$ s’obtient en ajoutant une solution particulière de cette équation avec second membre à la solution générale de l’équation différentielle homogène $ay'(t)+by(t)=0$.
La forme de l'ensemble des solutions de l’équation différentielle $ay'(t)+by(t)=c(t)$ s'appelle la solution générale de l’équation différentielle $ay'(t)+by(t)=c(t)$.
Voici la méthode à suivre pour trouver résoudre une équation différentielle avec second membre $ay'(t)+by(t)=c(t)$.
-
Étape 1 :
Chercher la solution générale $y_1$ de l’équation homogène $ay'(t)+by(t)=0$. -
Étape 2 :
Chercher une solution particulière $y_2$ de l’équation avec second membre $ay'(t)+by(t)=c(t)$. -
Étape 3 :
Conclure que la solution générale de l’équation $ay'(t)+by(t)=c(t)$ est la somme $y=y_1+y_2$.
Dans ce BTS, la forme d'une solution particulière sera toujours donnée dans l'énoncé.
Le but est de résoudre sur $\mathbb{R}$ l’équation différentielle $(E)$ : $y'(t)=5y(t)+e^{4t}$.
-
Déterminer, à la main si possible, la solution générale $y'(t)=5y(t)$.
-
Vérifier que la fonction $g$ définie par $g(t)=-e^{4t}$ est une solution particulière de $(E)$.
-
En déduire la solution générale de $(E)$ : $y'(t)=5y(t)+e^{4t}$.
-
Saisir sur Xcas
desolve(y'=5*y+e^(4*x),y).
Que sugnifie l'affichage obtenu ?
Exercices
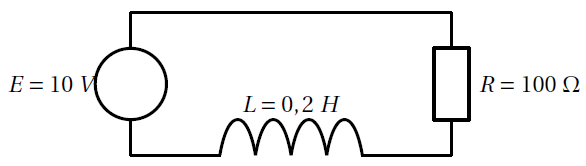
Un circuit électrique est constitué d’un générateur de f.e.m. $E$ en série avec une bobine d’inductance $L$
et de résistance $R$. L’intensité du courant $i$ est solution de l’équation différentielle (1) : $Li'(t)+Ri(t)=E$.
-
Montrer que l'intensité du courant vérifie l'équation différentielle (2) : $0.2y'(t)+100y(t)=10$.
-
Résoudre à la main l’équation différentielle (2) : $0.2y'(t)+100y(t)=0$.
-
Vérifier que la fonction $i$ définie sur $\mathbb{R}$ par $i(t)=0.1-0.1e^{-500t}$ est une solution de (1).
-
Dresser le tableau de variations complet de $i$ sur $[0;+\infty[$.
-
Déterminer l’instant $t_1$ à partir duquel l’intensité $i(t)$ sera supérieur à 0.095 A.
La température de refroidissement d’un objet en fonction du temps est donnée par une fonction $f$
définie sur $[0;+\infty[$ qui vérifie l’équation : $f'(t)+ 12 f(t)=10$.
La température est donnée en degrés Celsius et le temps en heures.
-
Sachant que pour $t=0$, la température de l’objet est 220°C, déterminer l'expression de $f(t)$ pour $t\gt 0$.
-
Étudier les variations de la fonction $f$ sur $[0;+\infty[$ ainsi que la limite de $f$ en $+\infty$.
-
-
Déterminer la valeur exacte du moment où la température de l’objet est 50 °C.
-
Arrondir ce moment à la minute près.
-
Pour un signal d'entrée de puissance $a$ fixée, la puissance lumineuse à la sortie d'une fibre optique dépend de sa longueur $x$,
longueur exprimée en kilomètres.
On considère une fibre optique pour laquelle la perte relative de puissance lumineuse est de 20%.
On peut modéliser la puissance $f(x)$ de sortie en fonction de la longueur $x$ comme solution sur $[0;+\infty[$
de l'équation différentielle $y'=-0.2y$ avec $y(0)=a$.
-
On mesure à 8 kilomètres de l'entrée de la fibre une puissance de 2 mW. Quelle est la puissance du signal à l'entrée de la fibre ?
-
Déterminer la longueur de la fibre à partir de laquelle la puissance du signal de sortie sera inférieure à 1 mW.
-
Déterminer la valeur moyenne de la puissance sur les 10 premiers kilomètres de la fibre.
Un embrayage vient appliquer, à l’instant $t=0$, un couple résistant constant sur un moteur dont la vitesse à vide est de 150 rad/s.
On note $\omega(t)$, la vitesse de rotation du moteur à l’instant $t$.
On admet que la fonction $\omega$ est solution de l’équation différentielle : $\dfrac{1}{200} y'(t)+y(t)=146$ $(E)$, où $y$
désigne une fonction dérivable de la variable réelle positive $t$.
-
-
Déterminer à la main si possible la solution générale de l’équation différentielle $(E_0)$ : $\dfrac{1}{200} y'(t)+y(t)=0$.
-
Chercher une solution particulière constante $c:t\mapsto C$ de $(E)$.
-
Sachant que $\omega(0)=150$, montrer que $\omega(t)=146+4e^{-200t}$ pour tout $t\in[0;+\infty[$.
-
-
-
On note $\displaystyle \omega_{\infty}= \lim_{t\to +\infty} \omega(t)$.
Déterminer la perte de vitesse $\omega(0)-\omega_{\infty}$ due au couple résistant. -
On considère que la vitesse du moteur est stabilisée lorsque l’écart relatif $\dfrac{\omega(t)-\omega_{\infty}}{\omega_{\infty}}$ est inférieur à 1 %.
Calculer le temps mis par le moteur pour stabiliser sa vitesse.
On donnera la valeur exacte et la valeur arrondie au millième.
-
Une entreprise achète à l'instant initial noté t=0 du matériel informatique qui nécessite un investissement de
1500 milliers d'euros. Cet investissement se déprécie. Sa dépréciation à l'instant $t$, exprimé en années, est noté $g(t)$.
On admet que la fonction $g$ est la solution sur l'intervalle $[0;10]$ de l'équation différentielle :
$y'=-0.08y+120$ avec $g(0)=0$.
-
Résoudre l'équation $y'=-0.08y$.
-
Déterminer le réel $a$ pour lequel la fonction constante $f$ telle que $f(t)=a$ est solution de $y'=-0.08y+120$.
-
En déduire l'ensemble des solutions de l'équation différentielle $y'=-0.08y+120$.
-
Déterminer la fonction $g$.
-
Déterminer au bout de combien d'années l'investissement aura perdu 60% de sa valeur.
-
Est-ce que l'investissement conservera à très long terme une partie de sa valeur ?
Le trafic internet au terminal informatique d'une grande société est modélisé par une fonction $f$
telle que $f(t)$ est la probabilité que le temps séparant deux paquets de données soit inférieur à $t$ secondes.
On admet que $f$ est la solution de l'équation différentielle $y'+710y=710$ telle que $f(0)=0$.
-
La probabilité $f(t)$ augmente ou diminue-t-elle lorsque le temps $t$ augmente ? Justifier.
-
À quel(s) instant(s) cette probabilité est-elle de 0.5 ?
-
Déterminer le temps moyen en secondes séparant l'arrivée de deux paquets de données.
Un processeur voit sa température, en degré Celsius, exprimée par une fonction $f$ en fonction du temps $t$, en heure.
On admet que $f$ vérifie l'équation différentielle $y'= \dfrac{1}{10} y+1$ et que sa température initiale est de 20°C.
-
Déterminer à l'aide de Xcas l'expression de la fonction $f$.
-
Le processeur arrête de fonctionner quand sa température dépasse 120°C.
Combien de temps fonctionnera ce processeur ?
On se propose d’obtenir l’intensité $i$ du courant dans le circuit ci-contre lorsqu’il est alimenté par le signal d’entrée $e$.
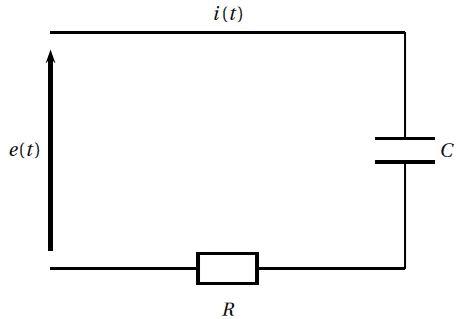
On admet que le courant $i$ vérifie l'équation différentielle suivante $(E)$ : $Ri'(t)+ \dfrac{1}{C}i(t)=e'(t)$.
On suppose que le signal d'entrée $e$ est un courant alternatif définit par $e(t)=1000\times \sin(2t)$, que $R=5000\Omega$ et $C=10^{-4} F$.
-
Réécrire l'équation différentielle $(E)$ avec les données admise du circuit.
-
Résoudre sur Xcas l'équation différentielle $5i'(t)+10i(t)=2\cos(2t)$.
-
Grâce à Xcas, exprimer en fonction des paramètres $R$ et $C$ la solution de l'l'équation différentielle $(E)$ : $Ri'(t)+ \dfrac{1}{C}i(t)=e'(t)$ avec la condition initiale $i(0)=0$.
Dans une entreprise, lors d’une intervention sur la sécurité routière, on s’intéresse au taux d’alcool dans le sang. Dans cet exercice, ce taux sera utilisé sans précision de l’unité.
Partie A : résolution d'une équation différentielle
On considère l’équation différentielle, notée $(E)$ : $y'+y=2e^{-t}$, où $y$ désigne une fonction de la variable
réelle $t$, définie et dérivable sur l’intervalle $[0.025;+\infty[$.
On admet que la fonction $f$ donnant le taux d'alcool en fonction du temps après ingestion d'une certaine quantité d'alcool.
-
Résoudre à la main l’équation différentielle $y'+y=0$.
-
Déterminer la valeur du réel $a$ telle que la fonction $g$ définie sur l’intervalle $[0,025;+\infty[$ par $g(t)=ate^{-t}$ soit une solution particulière de l’équation différentielle $(E)$.
-
En déduire la solution générale de l’équation différentielle $(E)$.
-
Déterminer à la main la fonction $f$ solution de l’équation différentielle $(E)$ qui vérifie $f(0.025)=0$.
-
Utiliser Xcas pour retrouver l'expression de $f(t)$ en fonction du temps $t$.
Partie B : lectures graphiques
Une personne a ingéré une certaine quantité d’alcool.
On s’intéresse à l’évolution du taux d’alcool dans le sang de cette personne, en fonction du temps $t$, en heures.
Compte tenu du délai d’absorption par l’organisme, le taux d’alcool dans le sang de cette personne est donné par la fonction $f$
définie sur $[0.025;+\infty[$ par $f(t)=(2t-0,05)e^{-t}$.
La représentation graphique est donnée ci-après : 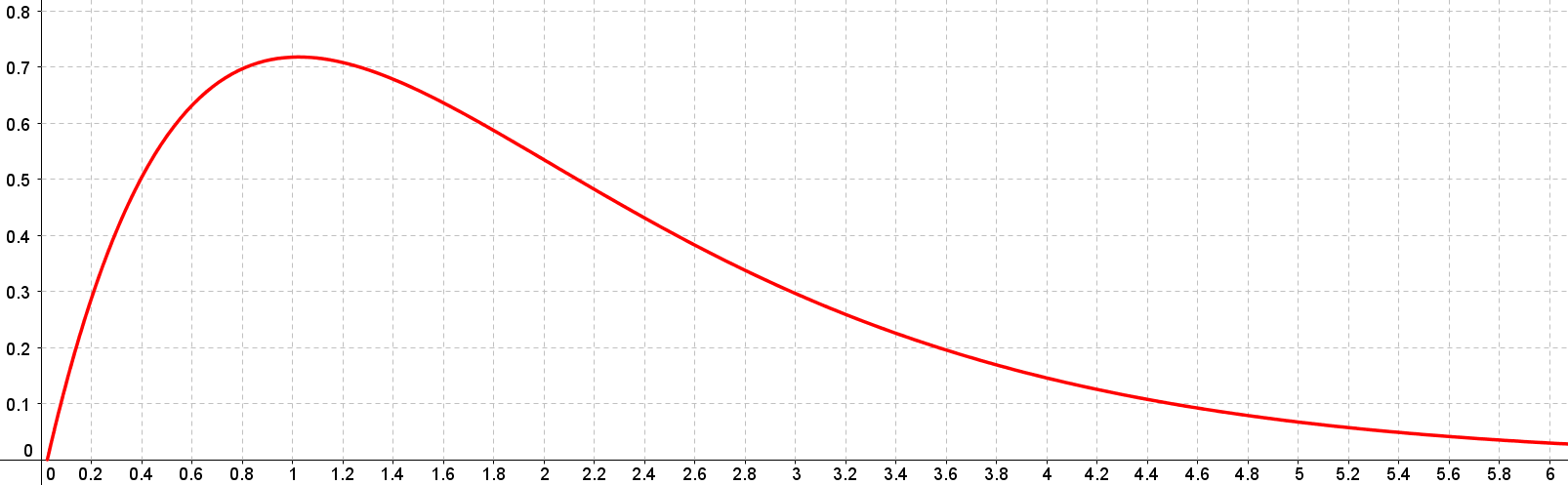
-
Déterminer, à l’aide du graphique ci-dessus, pendant combien de temps le taux d’alcool dans le sang de cette personne reste supérieur à 0.5.
-
Déterminer, à l’aide du graphique, à quel instant le taux est maximum et donner ce maximum.
-
Retrouver la valeur exacte de ces résultats sur Xcas.
Partie C : étude de fonction
-
Dresser le tableau de variations complet de $f$ sur $[0.025;+\infty[$.
-
On considère $\displaystyle T_m=\dfrac{1}{2} \int_2^4 f(t)dt$. $T_m$ est le taux d’alcool moyen entre les instants $t=2$ et $t=4$.
Calculer la valeur exacte de $T_m$ et en donner une valeur arrondie à 0.01 près.
De retour à l’école, Ali apprend que la température de refroidissement du pain à la sortie du four dépend du type
de pain et de la température ambiante supposée constante de la pièce dans laquelle il est entreposé.
On note $a$ cette température constante de la pièce, exprimée en degrés Celsius.
Pour $t\ge 0$, on désigne par $y(t)$ la température du pain au bout d’un temps $t$ après sa sortie du four.
La durée $t$ est exprimée en heures et la température $y(t)$ est exprimée en degrés Celsius.
Partie A : représentation graphique
-
Parmi les trois courbes suivantes, quelle est celle qui correspond à l’évolution de la température du pain à la sortie du four en fonction du temps ? Argumenter votre réponse.
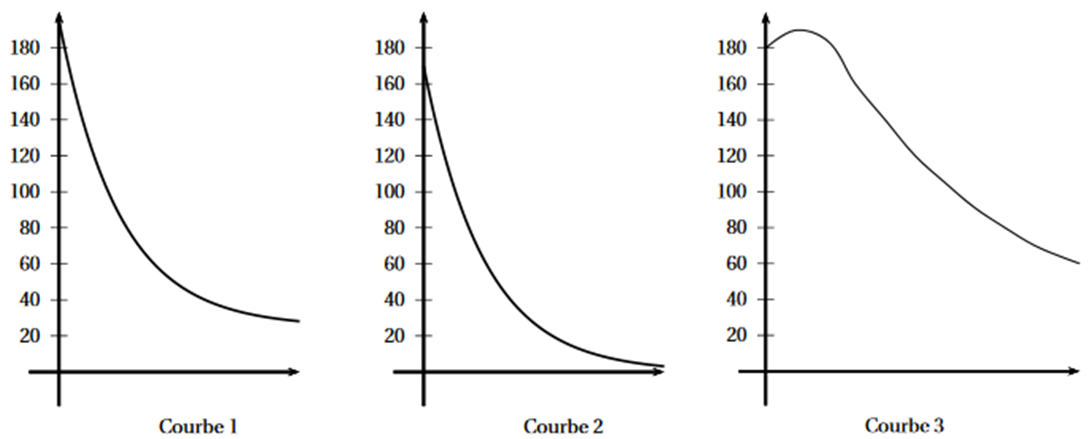
Dans toute la suite, la fonction $y$ vérifie l’équation différentielle : $(E)$ : $y'(t)+6y(t)=6a$.
Partie B : résolution d'une équation différentielle
Dans cette partie B on considère que le pain est entreposé dans une pièce dont la température constante est $a$. À la sortie du four, c’est-à-dire à l’instant $t=0$, le pain est à une température de 180°C.
-
Déterminer les solutions sur $[0;+\infty[$ de l’équation $(E_0)$ : $y'+6y=0$.
-
Soit $g$ la fonction définie sur l’intervalle $[0;+\infty[$ par $g(t)=k$, où $k$ est une constante réelle dépendant de $a$.
Déterminer $k$ pour que la fonction $g$ soit une solution particulière de l’équation différentielle $(E)$. -
En déduire l’ensemble des solutions de l’équation différentielle $(E)$.
-
Démontrer que la fonction $h$ définie sur l’intervalle $[0;+\infty[$ par $h(t)=(180-a)e^{-6t}+a$ est la solution de $(E)$ correspondant à la condition initiale donnée.
Partie C : étude de fonction
-
Dans cette question, le pain est entreposé à une température de 28°C.
-
Déterminer l'expression de la fonction $f$, définie pour tout $t\ge 0$, qui donne la température du pain au bout d’un temps $t$ après sa sortie du four.
-
Étudier les variations de $f$ sur l’intervalle $[0;+\infty[$.
-
Déterminer la température $\theta$ du pain une demi-heure après la sortie du four. On donnera une valeur approchée de $\theta$ à un degré près.
-
Le boulanger sort une fournée de pains du four. Déterminer par la méthode de votre choix au bout de quelle durée $D$ le pain sera à une température de 62°C. On donnera une valeur approchée de $D$ à une minute près.
-
-
Quelle devrait être la température, au degré près, de la pièce dans laquelle est entreposé le pain afin que ce pain, sorti du four à 16 h, soit à une température de 30°C à 16 h 30 ?
Une citerne calorifugée est chauffée par une résistance.
La température $\theta(t)$ de la citerne à l'instant $t$ vérifie l'équation différentielle
$y'= \dfrac{2}{100}-\dfrac{232}{10^6} y$, où $t$ est exprimé en seconde et $\theta$ en °C.
-
Sachant qu'au bout de 30 secondes de chauffe, l'eau contenue dans la citerne est à 20°C, déterminer l'expression de $\theta(t)$ en fonction de $t$.
-
Déterminer le sens de variations de $\theta$ sur $[0;+\infty[$.
-
Quelle était la température de l'eau initialement ?
-
Quelle sera la température de l'eau à très long terme si l'on continue à chauffer ?
-
Au bout de combien de temps la température atteint-elle 80°C ?
-
La sonde permettant d'évaluer la température de l'eau contenue dans la citerne a un temps de latence : à un instant $t$, elle ne mesure précisément la température $\theta(t)$ mais plutôt la température moyenne de l'eau sur les 10 secondes précédant $t$.
Déterminer la température mesurée par la sonde au bout de 2 minutes de chauffe.
Partie A : résolution d’une équation différentielle
On considère l’équation différentielle $(E)$ : $y'+2y=2e^{-2t}$ où $y$ est une fonction de la variable $t$, définie et dérivable sur un intervalle $[0;+\infty[$, et $y'$ la fonction dérivée de $y$.
-
Déterminer les solutions sur l’intervalle $[0;+\infty[$ de l’équation différentielle $(E_0)$ : $y'+2y=0$.
-
$h$ est la fonction définie sur $[0;+\infty[$ par : $h(t)=2te^{-2t}$.
Démontrer que $h$ est une solution particulière de $(E)$. -
En déduire l’ensemble des solutions de l’équation différentielle $(E)$.
-
Déterminer la solution $f$ de l’équation $(E)$ qui prend la valeur 1 pour $t=0$.
-
Vérifier le résultat obtenu avec Xcas.
Partie B : étude d’une fonction
$f$ est la fonction définie sur $[0;+\infty[$ par : $f(t)=(1+2t)e^{-2t}$.
$\mathcal{C}_f$ est la courbe représentative de f dans un repère orthogonal.
-
Déterminer la limite de $f(t)$ lorsque $t$ tend vers $+\infty$.
-
Construire le tableau de variations de $f$ sur $[0;+\infty[$.
-
Vérifier en traçant la courbe $\mathcal{C}_f$ avec GeoGebra.
Partie C : réfractomètre
Dans les régions viticoles, on peut contrôler le taux de sucre du raisin avec un réfractomètre à mesure rapide.
Le taux de défaillance du réfractomètre dans l’intervalle de temps $[0;+\infty[$ peut être modélisé par la fonction $g$ définie sur
$[0;+\infty[$ par : $g(t)=1-f(t)=1-(1+2t)e^{-2t}$ où $t$ est exprimé en heures et $f$ la fonction de la partie B.
-
-
Quel est le taux de défaillance du réfractomètre au bout d’une heure ?
-
Quel est le taux de défaillance du réfractomètre au bout de deux heures ?
-
-
Pour des raisons de fiabilité, on doit changer le réfractomètre lorsque le taux de défaillance est supérieur ou égal à 0.75. Déterminer la durée d’utilisation du réfractomètre, arrondir à $10^{-2}$.
Dans les deux questions suivantes, on donnera les valeurs exactes et les valeurs arrondies à $10^{-2}$.
Lors du processus de fabrication de plats cuisinés en restauration collective, le refroidissement est une phase
cruciale pour éviter la croissance de germes.
La réglementation impose que le refroidissement rapide des barquettes
de plats cuisinés soit opéré de telle manière que leur température ne demeure pas à des valeurs comprises entre +10 °C
et +63 °C pendant plus de 2 heures (arrêté du 8 octobre 2013, dispositions particulières applicables aux établissements
de restauration collective).
Une entreprise de restauration collective fabrique des barquettes de plats cuisinés, soumises à une attention
particulière : lorsqu’elles ont atteint une température de +63 °C, elles sont placées dans une cellule de
refroidissement rapide.
La température de la barquette est modélisée par une fonction $f$, qui, à tout temps $t$ en heures,
associe la température $f(t)$ de la barquette en °C.
On admet que la fonction $f$ est solution de l’équation différentielle $y'=-1.2(y-3)$ sur $[0;+\infty[$ avec $f(0)=63$.
-
Déterminer l'expression de $f(t)$ en fonction de $t$.
-
La réglementation est-elle respectée par l'entreprise de restauration rapide ?
-
Quelle est la température de la barquette à très long terme ?
-
Quelle est la température moyenne de la barquette sur les 90 premières minutes de refroidissement ?
La loi de refroidissement de Newton s’énonce ainsi : « la vitesse de refroidissement d’un corps chaud inerte est proportionnelle à la différence de température entre ce corps et le milieu ambiant. »
On appelle $T_0$ la température (en °C) du milieu ambiant, $f(t)$ la température (en °C) d’un produit chimique à l’instant
$t$ (en minutes).
D’après la loi énoncée, $f$ est solution de l’équation différentielle : $(E)$ : $y'=ay-T_0$ où $y$ est une fonction de variable
$t$ définie et dérivable sur $[0;+\infty[$, $y'$ sa fonction dérivée et $a$ un coefficient de proportionnalité (avec $a\neq 0$).
-
Résoudre sur $[0;+\infty[$ l’équation différentielle $(E_0)$ : $y'-ay=0$.
-
Déterminer un réel $c$ tel que la fonction $h$ constante définie sur $[0;+\infty[$ par $h(t)=c$ soit une solution particulière de l’équation différentielle $(E)$.
-
En déduire la solution générale de $(E)$.
-
Dans une pièce où la température est $T_0=20$ °C, une personne verse dans un récipient un produit chimique dont la température initiale est 80 °C.
Montrer que la température du produit à l’instant $t$ vérifie : $f(t)=60e^{at}+20$, où $a$ est le coefficient de proportionnalité défini précédemment. -
Sachant que 2 minutes plus tard, le produit est à 60 °C :
-
Déterminer par le calcul algébrique la valeur exacte de $a$.
-
Vérifier que $a\approx -0,2$.
-
Plusieurs projets de train à très haute vitesse et à propulsion électromagnétique sont en préparation, à
l’image de l’Hyperloop. Les wagons ont une forme cylindrique et sont propulsés dans un tube à basse pression afin de
réduire les frottements.
Les ingénieurs ont fixé comme objectif impératif pour le départ de chaque wagon d’atteindre en moins de 2 minutes une vitesse
instantanée de $400 km.h^{-1}$.
On note $f(t)$ la distance parcourue par le wagon, en $km$, à l’instant $t$ en minute.
On suppose que $f$ est une fonction de la variable $t$ définie et dérivable sur l’intervalle $[0;12]$.
L’objectif de cet exercice est d’étudier la fonction $f$ afin de vérifier les caractéristiques du départ.
Partie A. Résolution d’une équation différentielle
En appliquant les contraintes physiques et technologiques du projet, de premiers résultats conduisent à l’équation différentielle $(E)$ : $y'-0.2y=3t$, où $y$ est une fonction inconnue de la variable réelle $t$, définie et dérivable sur l’intervalle $[0;+\infty[$ et $y'$ la fonction dérivée de $y$.
-
Résoudre sur $[0;+\infty[$ l’équation différentielle $(E_0)$ : $y'-0.2y=0$.
-
Vérifier que la fonction $g$, définie sur $[0;12]$ par $g(t)=-15t-75$, est une solution de l’équation différentielle $(E)$.
-
En déduire l’ensemble des solutions de l’équation différentielle $(E)$.
-
Au temps $t=0$, le wagon est au point de départ. Déterminer la fonction $f$ solution de $(E)$ telle que $f(0)=0$.
-
Vérifier sur Xcas la solution de $(E)$ $f$ trouvée vérifiant la condition initiale $f(0)=0$.
Partie B. Étude de fonction et application
On considère la fonction $f$ définie sur l’intervalle $[0;12]$ par $f(t)=75(e^{0.2t}-1)-15t$.
-
Déterminer les variations de la fonction $f$ sur $[0;12]$.
-
Déterminer le nombre de kilomètres parcourus au bout d’une minute. Arrondir le résultat au dixième.
-
-
La vitesse du wagon, en kilomètre par minute, à l’instant $t$, correspond à $f'(t)$.
En déduire la vitesse, en kilomètre par minute, du wagon à $t=2$ minutes. Arrondir le résultat au dixième. -
L’objectif des ingénieurs est-il atteint ? Justifier la réponse.
-
-
Déterminer le temps nécessaire, à la seconde près, pour que le wagon atteigne $400 km.h^{-1}$.
Partie C. Étude du profil d'une gare
Afin d’aménager les futures gares dédiées à ce train à très haute vitesse, les architectes ont dessiné la pièce suivante,
représentée dans un repère orthonormé avec pour unité graphique 1 mètre sur les deux axes.
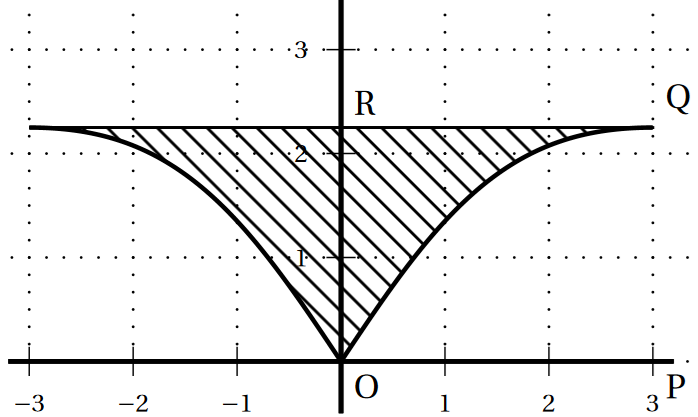
On désire calculer de façon précise l’aire $\mathcal{A}$ de la surface hachurée sur le dessin ci-dessus.
Pour cela on dispose des données suivantes :
-
la pièce est symétrique par rapport à l’axe des ordonnées ;
-
le bord supérieur correspond à la droite d’équation $y=2.25$ ;
-
le bord inférieur droit correspond à la fonction $g$ définie sur l’intervalle $[0;3]$ par : $g(x)=\dfrac{27x}{2x^2+18}$.
-
Déterminer l'aire $\mathcal{A}$, en unité d'aire, arrondie au millième.
La vitesse ve d'écoulement d'un fluide dans un tube cylindrique est solution de l'équation différentielle $(E)$ : $4v'+v=3e^{\frac{x}{2}}-1$, où $v$ est une fonction de la variable $x$, définie et dérivable sur $[0;+\infty[$, et $v'$ est la dérivée de $v$.
-
Résoudre l'équation différentielle $(E_0)$ : $4v'+v=0$.
-
Déterminer les réels $A$ et $B$ pour que la fonction $u$ telle que $u(x)=Ae^{\frac{x}{2}}+B$ soit une solution particulière de $(E)$.
-
En déduire l'ensemble des solutions de l'équation différentielle $(E)$.
-
Déterminer la solution particulière $v_e$ de l'équation différentielle $(E)$ vérifiant $v_e(0)=0$.
-
Vérifier sur Xcas.
Un réservoir contient 1000 litres d'eau douce dont la salinité est de 0.12 $g.L^{-1}$.
À la suite d'un accident, de l'eau de mer pénètre dans ce réservoir à raison de 10L par minutes.
On note $s$ la fonction donnant la salinité en fonction du temps $t$ en minutes. On admet que $s$ est solution de
l'équation différentielle : $s'(t)+0.01s(t)=0.39$.
Sachant que pour réduire les conséquences la salinité doit rester inférieure à 3.9 $g.L^{-1}$, de combien de temps
dispose le service de surveillance du réservoir pour arrêter l'arrivée d'eau salée ?
Pour tester la résistance d'une plaque phonique à la chaleur, on porte en laboratoire sa température à 100°C et on
étudie l'évolution de sa température en fonction du temps $t$ (en minutes).
Soit $\theta(t)$ la température (en degré Celsius) de la plaque à l'instant $t$ ($t$ exprimé en minutes).
La température ambiante du laboratoire est de 19°C et après 6 minutes la température est redescendue à 82°C.
En exploitant ces données, on peut démontrer (comme aux exercices 3 et 8) que la fonction $\theta$ est solution de
l'équation différentielle $(E)$ : $y'(t)+0.042y(t)=0.798$, où $y$ est la fonction inconnue, de variable $t$, définie
et dérivable sur l'intervalle $[0;+\infty[$.
-
Déterminer l'expression de $\theta(t)$ en fonction de $t$, lorsque $t\ge 0$.
-
Déterminer le temps nécessaire pour que la température de la plaque redescende en dessous de 30°C.
Demander le programme !
-
Savoir la forme générale d'une équation différentielle du premier ordre à coefficients constants : $ay'(t)+by(t)=f(t)$, avec $a\in\mathbb{R}$ et $b\in\mathbb{R}$.
-
Savoir la définition d'une équation différentielle homogène (ou sans second membre).
-
Savoir la formule de cours donnant l'ensemble des solutions d'une équation différentielle homogène : $Ke^{-\dfrac{b}{a}t}$ avec $K\in\mathbb{R}$.
-
Savoir qu'il peut exister une infinité de fonctions solutions à une équation différentielle du premier ordre donnée.
-
Savoir que rajouter une condition particulière à une équation différentielle conduit à l'unicité de la fonction solution cherchée.
-
Savoir vérifier à la main qu'une fonction est solution ou non d'une équation différentielle.
-
Savoir vérifier sur Xcas qu'une fonction est solution ou non d'une équation différentielle.
-
Savoir résoudre sur Xcas une équation différentielle, avec ou sans condition initiale.
-
Savoir utiliser une équation différentielle pour modéliser des problèmes concrets.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International