loi exponentielle

La loi exponentielle sert à estimer la durée de vie d'un système non soumis à l'usure (en électronique par exemple) et en ayant exclu les pannes précoces, tout comme le temps d'attente d'un événement accidentel (tremblement de terre, désintégration radioactive, ...)

Introduction

Un noyau radioactif est instable est se désintègre, au bout d'un certain temps, en un noyau d'un autre type.
On considère un type de noyau radioactif dont la probabilité de se désintégrer dans une unité de temps est $p$ et on se demande quel temps on doit attendre pour qu'il se désintègre.

On va utiliser le tableur de Geogebra pour simuler une désintégration.
On admet que les lois physiques conduisent à devoir saisir dans une cellule la formule =(-ln(random())) / p où p est défini préalablement comme un curseur.
Voici le résultat d'une simulation :
Cela signifie que le noyau radioactif considéré s'est désintégré au bout de 1.83 unités de temps.
Vous pouvez lancer une nouvelle simulation en appuyant sur les touches CTRL+R ; surement, une autre valeur apparaîtra.

Vous pouvez trouver ces simulations directement dans ce fichier Geogebra embarqué ; il vous suffira de cliquer sur l'icône pour avancer dans la présentation :

En reproduisant cette formule sur le tableur, on peut simuler facilement le temps à attendre pour chacune de 10000 désintégration. Ces temps ont été stockés dans un tableau de valeurs :

Pour visualiser, l'ensemble des valeurs est représenté par un histogramme à n intervalles, où n est un curseur permettant de varier la valeur parmi les entiers entre 1 et 100.
En ordonnée, on considère la fréquence de chaque intervalle.
Voici un exemple d'histogramme des fréquences de désintégration par tranche d'unité de temps dans le cas où on découpe en n=20 intervalles et que l'on simule 10000 désintégrations, chacune ayant une probabilité p=0.4 de se produire en unu unité de temps :

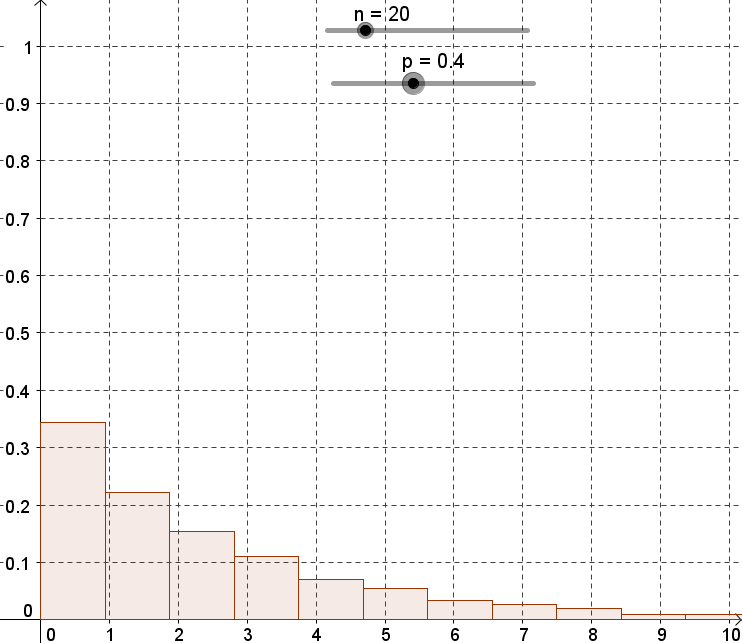
En simulant d'autres séries aléatoires de 10000 désintégrations, vous pouvez observer une fluctuation de l'histogramme. Cependant, comme la forma globale est similaire à chaque simulation, On cherche à approcher cet histogramme par une loi continue.
Pour cela, on a superposé la courbe représentant la fonction $f$ définie sur $[0;+\infty$[ par $f(t)=pe^{-pt}$, où $p$ est la probabilité qu'un atome se désintègre en une unité de temps.
On obtient le graphique suivant :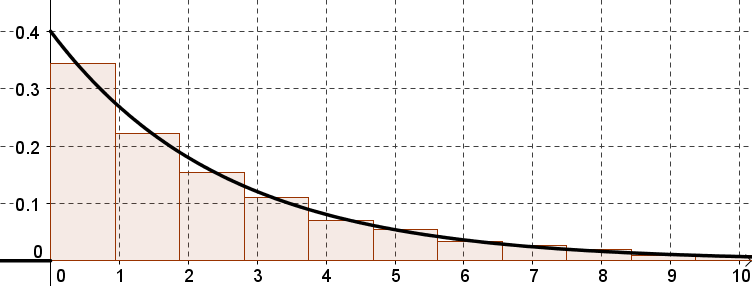

Que pensez-vous de l'approximation obtenue précédemment ?
Comment évolue cette approximation lorsque le nombre de rectangles de l'histogramme augmente ?
Voici une autre simulation avec une autre valeur de p et un nombre de rectangles supérieur pour l'histogramme :
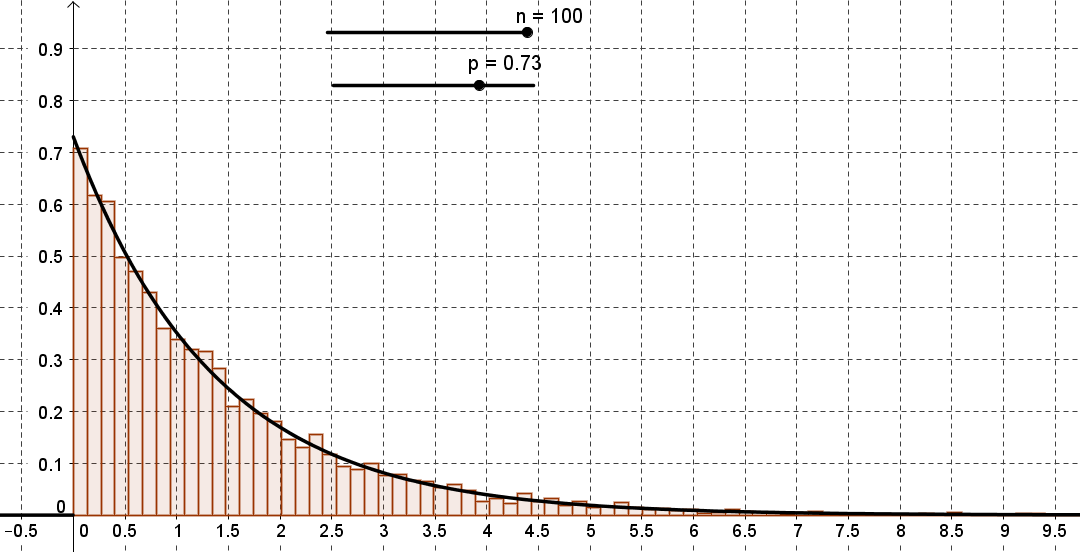
Comment faire pour approcher la probabilité qu'un noyau se désintègre entre 1 et 3 unités de temps ?

Définition et propriétés

On reprend la fonction introduite précédemment : $f(t)=pe^{-pt}$.
Cependant pour ne pas confondre le $p$ avec le $P$ signifiant que l'on calcule une probabilité, on remplace la lettre $p$ par celle grecque $\lambda$.
Dans l'exemple précédent, $X$ représente une variable aléatoire donnant le temps que met un certain noyau radioactif pour se désintégrer :

Soit $\lambda$ un réel strictement positif et $f_{\lambda}$ la fonction définie sur $I=[0;+\infty[$ par $f_{\lambda}(t)=\lambda\times e^{-\lambda t}$.
Une variable aléatoire $X$ suit une loi exponentielle de paramètre $\lambda$ si sa densité de probabilité est la fonction $f_{\lambda}$ en posant :

On parle aussi de loi sans vieillissement, terminologie qui sera justifiée dans la suite du chapitre.

Cette loi continue dont les probabilités sont définies par les intégrales suivantes :

Formule de calcul exact

Si $X$ suit une loi exponentielle de paramètre $\lambda$, alors :

Pour tout réel $a$ et $b$ de $I$, $\displaystyle P(X\in [a;b])=\int_a^b \lambda\times e^{-\lambda t} dt$.
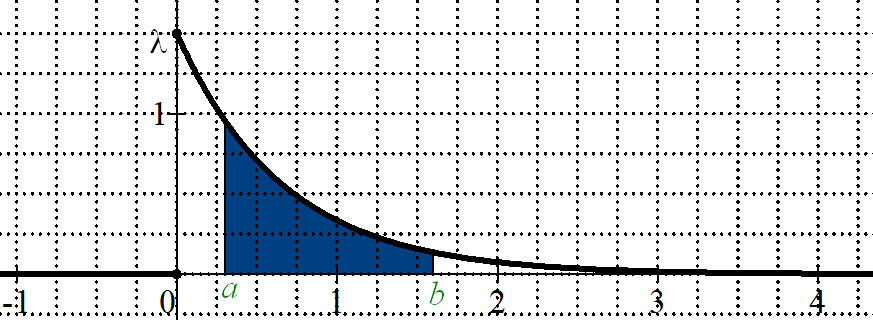
Pour tout réel $a$ de $I$, $\displaystyle P(X\in [a;+\infty[)=1-P(X\in [0;a])=\int_0^a \lambda\times e^{-\lambda t} dt$.

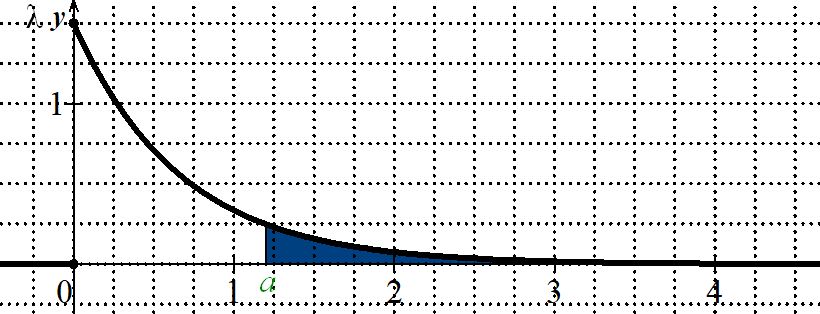
Comme la notion d'intégrale (généralisée) sur un intervalle de la forme $[a;+\infty[$) est hors-programme, l'idée est de se ramener à un intervalle borné de la forme $[a;b]$ pour calculer l'intégrale en utilisant la probabilité de l'événement contraire car : $\overline{[a;+\infty[}=[0;a[$ et $P([0;a[)=P([0;a])$.

Pour calculer ces probabilités définies par une intégrale, vous aurez deux possibilités dans ce BTS :

soit les calculer à la main (de manière exacte) à l'aide d'une primitive selon la propriété suivante,
soit obtenir directement sur Geogebra une valeur approchée de l'intégrale.

Comme $t\mapsto \lambda \times e^{-\lambda t}$ a pour primitive sur $[0;+\infty[$ la fonction $t\mapsto -e^{-\lambda t}$, on peut calculer les intégrales précédentes ainsi :

Pour tout réel $a$ et $b$ de $I$, $\displaystyle P(X\in [a;b])=\int_a^b \lambda\times e^{-\lambda t} dt$ $\displaystyle =[-e^{-\lambda t}]^b_a=e^a-e^b$.
Pour tout réel $a$ de $I$, $\displaystyle P(X\in [a;+\infty[)=1-P(X\in [0;a])=\int_0^a \lambda\times e^{-\lambda t} dt$ $\displaystyle =1-[-e^{-\lambda t}]^a_0=1-(e^0-e^a)=e^a$.

La valeur du paramètre $\lambda$ peut être lue directment sur le graphique représentant la densité au niveau de l'axe des ordonnées.
En effet, $f(0)=\lambda\times e^0=\lambda$.

Utilisation de Geogebra

Si $X$ suit une loi exponentielle de paramètre $\lambda=0.73$, alors pour calculer $P(X\in [2;+\infty[)$, il suffit :

dans Geogebra, ouvrir Calculs de probabilités à partir de l'onglet affichage.
Sélectionner la loi exponentielle.
Saisir comme valeur du paramètre $\lambda$ le nombre ici 0.73.
Sélectionner le type d'intervalle correspondant à celui recherché. Ici, pour $[2;+\infty[$.
Saisir la ou les bornes de l'intervalle. Ici 2.
Il suffit alors de lire la valeur approchée proposée par Geogebra ; ici 0.2322.

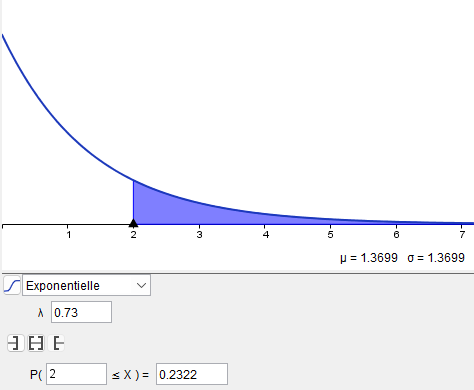
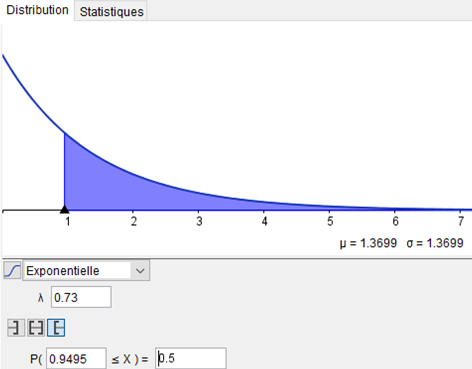
On reprend la variable aléatoire $X$ suivant la loi exponentielle de paramètre $\lambda=0.73$.
Pour trouver une borne de l'intervalle liée à une probabilité fixée, par exemple pour trouver le réel $a$ stritement positif tel que $P(X\ge a)=0.5$, il suffit de remplacer les deux dernières étapes de l'exemple précédent par :

Sélectionner le type d'intervalle correspondant à celui recherché. Ici, pour $X\ge a$.
Saisir la probabilité connue. Ici 0.5.
Il suffit alors de lire la valeur approchée proposée par Geogebra pour $a$ ; ici 0.9495.

Il est possible d'obtenir ces valeurs directement avec Xcas, mais sans la représentation graphique qui permet de faciliter la vérification de la cohérence :

exponential_cdf(λ,x,y) renvoie la probabilité $P(x\le X \le y)$ lorsque $X$ suit une loi exponentielle de paramètre $\lambda$.
exponential_icdf(λ,p) renvoie le réel $x$ tel que $P(0\le X\le x)=p$ lorsque $X$ suit une loi exponentielle de paramètre $\lambda$.

La durée de vie en heures d’une diode est une variable aléatoire $T$ suivant une loi exponentielle de paramètre 0.0008.

Calculer la probabilité que la diode tombe en panne avant 4000 h de fonctionnement.
Calculer le temps de durée de vie médiane d'une diode, c'est à dire le temps $t$ tel que $P(T\le t)=0.5$.

Soit $X$ une variable aléatoire suivant une loi exponentielle de paramètre $\lambda$.

Son espérance mathématique est donnée par : $\displaystyle E[X]= \lim_{t\to +\infty} \int_0^x t\lambda e^{-\lambda t}dt= \dfrac{1}{\lambda}$.
Sa variance est donnée par : $\displaystyle V[X]= \lim_{t\to +\infty} \int_0^x \left(t-\dfrac{1}{\lambda} \right)^2\times \lambda e^{-\lambda t}dt= \dfrac{1}{\lambda^2}$.
Son écart-type est donné par : $\sigma[X]=\sqrt{V(X)} = \dfrac{1}{\lambda}$.

La valeur approchée de la moyenne et de l'écart-type sont directement lisibles dans le coin inférieur droit de la fenêtre de Geogebra ; la moyenne correspondant à $\mu$ et l'écart-type correspondant à $\sigma$.

La durée de vie en heures d’une diode est une variable aléatoire $T$ suivant une loi exponentielle de paramètre 0.0008.

Calculer le temps de durée de vie moyenne d'une diode.

Taux d'avarie et loi sans vieillissement

Soit $T$ la variable aléatoire qui à un "matériel" associe sa durée de bon fonctionnement avant défaillance.

On appelle fonction de défaillance la fonction $F:t\mapsto P(T\le t)$, (c'est-à-dire qui associe au temps $t$ la probabilité d'avoir une défaillance avant le temps $t$).

$F$ comme failure : défaillance en anglais.
On appelle fonction de fiabilité la fonction $R:t\mapsto P(T\ge t)$, (c'est-à-dire qui associe au temps $t$ la probabilité de ne pas avoir une défaillance avant le temps $t$).

$R$ comme reliability : fiabilité en anglais.
On appelle taux d'avarie instantanée le taux instantané de défaillance à l'instant $t$.

Le taux d'avarie est donné par $\lambda(t)=-\dfrac{R'(t)}{R(t)} =\dfrac{f(t)}{1-F(t)}$.

Si $T$ suit une loi exponentielle de paramètre $\lambda$, alors le taux d'avarie est constant au paramètre $\lambda$.

Ceci peut être aussi compris comme le fait qu'une loi exponentielle est une loi sans vieillissement :

Soit $T$ la variable aléatoire correspondant à la durée de vie d’un individu (au sens statistique).

On dit que $T$ suit la loi de durée de vie sans vieillissement si la probabilité que l’individu soit encore en vie à l’instant $t+h$ ($h\ge 0$), sachant qu’il est en vie à l’instant $t$, ne dépend pas de $t$ ($t\ge 0$).

Autrement dit : $P_{(T\ge t)}(T\ge t+h)=P(T\ge h)$.

Concrètement, cela signifie que vivre un temps $h$ supplémentaire ne dépend de l’âge $t$ déjà atteint.

Une variable aléatoire $T$ suit la loi de non vieillissement si, et seulement si, elle suit une loi exponentielle.

On considère de nouveau une diode dont la durée de vie est une variable aléatoire $T$ qui suit une loi exponentielle de paramètre 0.0008.
Sachant qu’elle a déjà fonctionné 1000 heures, calculer la probabilité qu’une diode fonctionne encore 500 heures.

Exercices

Soit $X$ une variable aléatoire qui suit une loi exponentielle de paramètre $\lambda$.
La courbe $\mathcal{C}_f$ ci-dessous représente la fonction de densité $f$ associée à $X$.

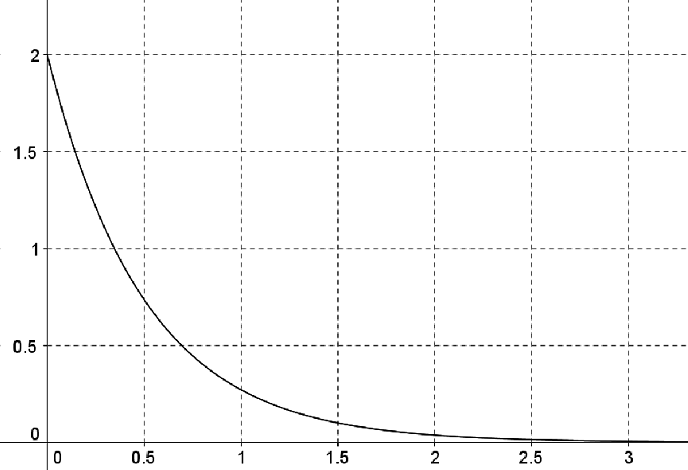
Où peut-on lire sur le graphique ci-dessus la valeur du paramètre $\lambda$ ? Justifier.
Reproduire à main levée, la courbe $\mathcal{C}_f$ ci-dessus puis représenter graphiquement les probabilités suivantes :
1. $P(X\le 0.5)$.
2. $P(X\ge 2)$.
3. $P(1\le X\le 1.5)$.
On suppose désormais que $\lambda=2$.
Calculer, à $10^{-4}$ près, les probabilités ou valeurs suivantes :
1. $P(X=0.5)$ puis $P(X\lt 0.5)$.
2. $P(X\le 2)$ puis $P(X\ge 2)$.
3. Calculer $t$ tel que $P(X\le t)=0.25$.
4. Calculer $t'$ tel que $P(X\le t')=P(X\ge t')$.

La durée de vie, exprimée en années, d’un composant électronique peut être modélisée par une variable aléatoire notée $X$ suivant la loi exponentielle de paramètre $\lambda$ avec $\lambda \gt 0$.
La courbe de la fonction densité associée est représentée ci-dessous :

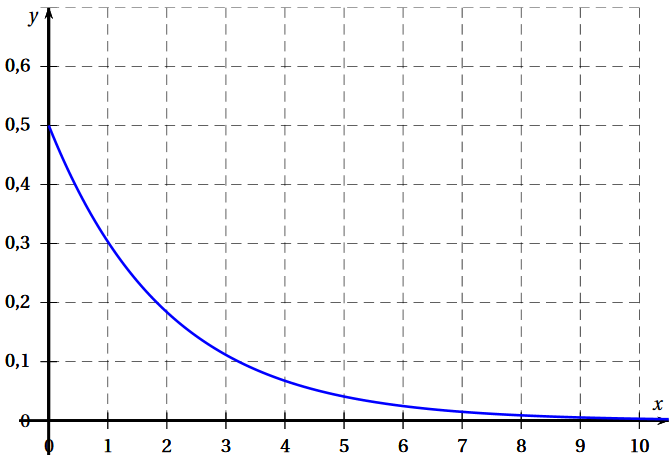
1. Reproduire à main levée le graphique ci-dessus.
2. Représenter la probabilité $P(X\le 1)$.
3. Indiquer où se lit directement la valeur de $\lambda$.
On suppose que $E(X)=2$.
1. Que représente dans le cadre de l’exercice la valeur de l’espérance mathématique de la variable aléatoire $X$ ?
2. Calculer la valeur de $\lambda$.
3. Calculer $P(X\le 2)$.
  Interpréter concrètement ce résultat.
4. Sachant que le composant a déjà fonctionné une année, quelle est la probabilité que sa durée de vie totale soit d’au moins trois années ? Expliciter la démarche mise en oeuvre.

On s’intéresse à un switch prélevé au hasard dans le parc de switches d'un ensemble de serveurs.
On désigne par $T$ la variable aléatoire qui, à tout switch au hasard dans le parc, associe la durée de vie avant une défaillance.

On note $P(T\gt t)$ la probabilité qu’un switch prélevé au hasard dans le parc n’ait pas une défaillance avant l’instant $t$, exprimé en jours. On suppose que $T$ suit une loi exponentielle de paramètre $\lambda=0.005$.

Calculer la probabilité qu’un switch prélevé au hasard dans le parc fonctionne plus de 200 jours sans panne.
Déterminer le temps $t$, arrondi à l’entier près, pour que la probabilité qu’un switch prélevé au hasard dans le parc fonctionne plus de $t$ jours, soit égale à 0.8.

La durée de vie, en années, d’une fibre optique fabriquée dans une usine est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda$ avec $\lambda \gt 0$.

La courbe représentative $\mathcal{C}$ de la fonction $f$ est donnée ci-dessous :
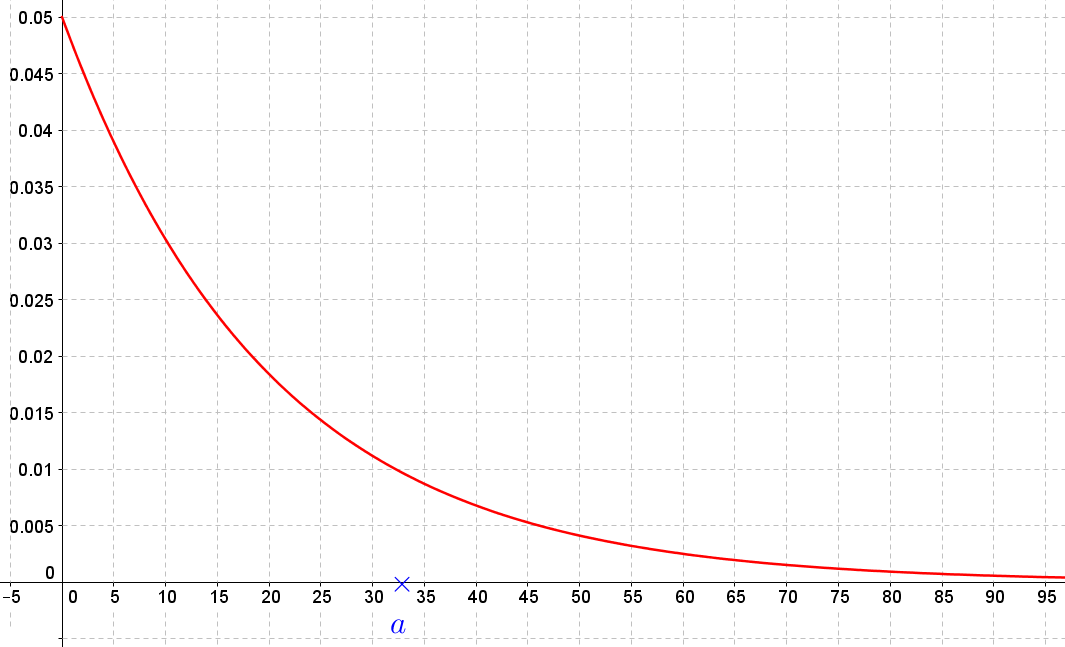
1. Reproduire à main levée la courbe $\mathcal{C}$ puis représenter graphiquement $P(T\ge a)$ où $a>0$.
2. Donner une valeur approchée du paramètre $\lambda$ grâce à la courbe $\mathcal{C}$.
Des études statistiques ont permis d'estimer que $P(T\ge 6)=0.74$.
Déterminer la valeur exacte de $\lambda$ puis celle approchée à $10^{-4}$ près.
Dans cette question, on prend $\lambda=0.05$.
1. Déterminer la durée de vie moyenne d'une fibre optique fabriquée dans cette usine.
2. On choisit au hasard une fibre optique fabriquée dans cette usine.
  Déterminer la probabilité que cette fibre fonctionne au moins 20 ans.
3. On choisit au hasard une fibre optique parmi celles qui fonctionnent encore au bout de 10 ans. Déterminer la probabilité que ce composant ait une durée de vie supérieure à 20 ans.
4. Déterminer la valeur $t$ telle que $P(T\ge t)$ soit égale à 0.5.
  Interpréter concrètement cette valeur.

Une entreprise fabrique des portails.
On admet que l'ouverture automatique des portails se fait grâce à un moteur dont la durée de vie, exprimée en années, est une variable aléatoire $X$ suivant la loi exponentielle de paramètres $\lambda$, avec $\lambda \gt 0$.

On sait que $P(X\le 2)=0.15$. Déterminer la valeur approchée à $10^{-4}$ près du réel $\lambda$.
Désormais, on prend comme valeur $\lambda=0.081$.
1. Calculer $P(X \gt 3)$.
2. Le moteur a déjà fonctionné durant 3 ans. Quelle est la probabilité pour qu’il fonctionne encore 2 ans ?
3. Calculer l’espérance de la variable aléatoire $X$ et donner une interprétation de ce résultat.

Une entreprise de services informatiques accueille des clients. Ceux-ci doivent être servis par des techniciens.
On admet que le temps d'attente, exprimé en minutes, d'un client pour être reçu par un technicien est une variable aléatoire $X$ suivant la loi exponentielle de paramètres $\lambda$, avec $\lambda \gt 0$.

Une étude statistique a permis d'observer que le temps d'attente moyen d'attente est de 4 minutes.

Déterminer la valeur exacte de $\lambda$.
Un nouveau client arrive. Quelle est la probabilité qu'il attende entre 2 et 5 minutes ?
Un client attend déjà dépuis 3 minutes. Quelle est la probabilité qu'il attende en tout moins de 5 minutes ?
Une réorganisation du service conduit désormais à ce que le temps médian d'attente soit de 4 minutes, c'est-à-dire que $P(X\le 4)=P(X\ge 4)=0.5$.
Le temps moyen d'attente est-il inchangé, réduit ou augmenté ? Justifier la réponse.

On modélise le temps d’attente, exprimé en minutes, à un guichet, par une variable aléatoire $T$ qui suit la loi exponentielle de paramètre 0.7.

Pour chacune des deux affirmations suivantes, préciser si elle est vraie ou fausse en justifiant la réponse.

Affirmation 1 :
La probabilité qu’un client attende au moins cinq minutes à ce guichet est 0.7 environ.
Affirmation 2 :
Le temps d’attente moyen à ce guichet est de sept minutes.

Vous gérez les serveurs d’une entreprise.
Vous décidez de mettre en place un système d'affichage des serveurs posant des problèmes grâce à des LED.
Vous faites acheter des diodes électroluminescentes (LED). Le producteur affirme que la durée de vie, en années, des diodes électroluminescentes est une variable aléatoire suivant une loi exponentielle de paramètre $\lambda$.

Sachant que le producteur de LED affirme dans sa documentation technique que la probabilité qu'une LED tombe en panne sur les cinq premières années est de 0.12, déterminer la valeur exacte de $\lambda$.

Dans la suite de l'exercice, on prendra $\lambda = 0.0256$.

Déterminer la probabilité que la LED fonctionne entre 10 et 30 ans.
Déterminer la durée de vie moyenne d'une LED si l'on en croit son fabricant.
Une LED fonctionne depuis 10 ans. Quelle est la probabilité qu'elle tombe en panne sur les 30 ans suivant ?

Liens avec des chapitres de première année

Une entreprise fabrique des puces électroniques qui sont utilisées pour des matériels aussi différents que des téléphones portables, des lave-linge ou des automobiles.
À la sortie de fabrication, 5 % d’entre elles présentent un défaut et sont donc éliminées. Les puces restantes sont livrées aux clients.
On dit qu’une puce a une durée de vie courte si cette durée de vie est inférieure ou égale à 1 000 heures. On observe que 2 % des puces livrées ont une durée de vie courte. On note :

$L$ l’évènement «La puce est livrée.».
$C$ l’évènement «La puce a une durée de vie courte c’est-à-dire inférieure ou égale à 1 000 heures.».

On tire au hasard une puce fabriquée par l’entreprise.
1. Donner la valeur de la probabilité $P_L(C)$.
2. Quelle est la probabilité que la puce soit livrée et ait une durée de vie strictement supérieure à 1 000 heures ?
3. Déterminer la probabilité que la puce soit éliminée ou ait une durée de vie courte à la sortie de la chaine de fabrication.

Dans la suite de l’exercice on s’intéresse seulement aux puces livrées aux clients.

On appelle $X$ la variable aléatoire correspondant à la durée de vie en heures d’une telle puce.
On suppose que $X$ suit une loi exponentielle de paramètre $\lambda$.
1. Montrer que $\lambda=- \dfrac{\ln(0.98)}{1000}$.
2. Calculer la probabilité qu’une puce ait une durée de vie supérieure à 10 000 heures.
3. Calculer $P(20000\le X\le 30000)$. Interpréter ce résultat.
4. Une puce a déjà duré 20000 heures. Quelle est la probabilité qu'elle dure encore moins de 10000 heures ?
Les ingénieurs de l’entreprise ont mis au point un nouveau procédé de fabrication.
On suppose qu’avec ce nouveau procédé la probabilité qu’une puce livrée donnée ait une durée de vie courte est égale à 0.003. On prélève au hasard 15 000 puces prêtes à être livrées.
On admettra que ce prélèvement de 15 000 puces revient à effectuer un tirage avec remise de 15 000 puces parmi l’ensemble de toutes les puces électroniques produites par l’entreprise et prêtes à être livrées.
On appelle $Y$ la variable aléatoire égale au nombre de puces ayant une vie courte dans cet échantillon.
1. Justifier que $Y$ suit une loi binomiale de paramètres à préciser.
2. Calculer l’espérance de la variable aléatoire $Y$. Interpréter ce résultat.
3. Calculer la probabilité $P(40\le Y\le 50)$.

On considère un transistor servant à fabriquer un microprocesseur.
On note $T$ la variable aléatoire qui, à tout transistor, prélevé au hasard dans un stock, associe sa durée de fonctionnement (en heures) avant une défaillance.
On suppose que $T$ suit une loi exponentielle de paramètre $\lambda$.
On désigne par $R$ sa fonction de fiabilité et par $F$ sa fonction de défaillance.

Donner l'expression de $R(t)=P(T\gt t)$ et de $F(t)=P(T\lt t)$ en fonction de $t$ et de $\lambda$.
À partir d'une étude statistique, le fabricant a pu évaluer que $R(2000)=0.8$.
Déterminer la valeur exacte de $\lambda$.
On prendra désormais $\lambda=0.0001$.
1. Donner le temps moyen de fonctionnement du transistor arrondi à l'heure prêt.
2. Calculer la probabilité qu'un transistor fonctionne plus de 3000 heures.
3. Un transistor a déjà fonctionné 2000 heures. Calculer la probabilité que ce transistor fonctionne plus de 3000 h.
4. Un transistor a déjà fonctionné 3000 heures, quelle est la probabilité qu'il subisse une défaillance dans les 1000 heures prochaines de fonctionnement.
5. Quelle est la durée de vie médiane d'un transistor, c'est à dire le temps $t_m$ tel que $P(T\ge t_m)=P(T\le t_m)$ ?
On admet dans cette question que les fonctionnements de deux transistors identiques sont indépendants.
On admet qu'un montage de deux composants en série fonctionne si les deux transistors fonctionnent simultanément et qu'un montage de deux transistors en parallèle fonctionne si au moins un des deux transistors fonctionne.
1. Quelle est la probabilité qu'un montage de deux composants en série fonctionne au delà de 3000 heures ?
2. Quelle est la probabilité qu'un montage de deux composants en parallèle fonctionne au-delà de 3000 heures ?
Le fabriquant vend ses transistors à 0.02€ tandis que le coût de fabrication est de 0.01€. Le fabricant promet de rembourser ses clients et de dédommager à hauteur de 0.05€ en cas de durée de vie inférieure à $t$.
1. Justifier que le bénéfice réalisé pour un transistor est donné par la fonction $B$ définie par : $B(t)=0.07\times e^{-\lambda t}-0.06$.
2. Déterminer la durée $t$ maximale donnant droit au remboursement qui permet à l'entreprise d'être bénéficiaire malgré le dédommagement.
3. Le conseil commercial propose de limiter à 2% des transistors la possibilité de remboursement.
  Quelle période de garantie doit proposer l'entreprise si elle suit le conseiller commercial ?
4. Quel est dans ces conditions le bénéfice réalisé par transistor vendu ?

Demander le programme !

La formule donnant la densité d'une loi exponentielle de paramètre $\lambda$.
La formule donnant l'espérance mathématique d'une loi exponentielle de paramètre $\lambda$.
Les notions de fiabilité et de défaillance.
Le fait qu'une loi exponentielle est une loi de probabilité sans vieillissement.
La représentation graphique d'une loi exponentielle de paramètre $\lambda$.

Savoir calculer sur Geogebra une probabilité liée à une loi exponentielle.
Savoir calculer sur Geogebra la borne d'un intervalle connaissant la probabilité asssociée à cet intervalle.
Savoir retrouver sur Geogebra une valeur approchée de l'espérance mathématique et de l'écart-type d'une loi exponentielle de paramètre $\lambda$.
Savoir exploiter la simulation d'un problème concret à l'aide d'une loi exponentielle.
Savoir interpréter concrètement l'espérance mathématique d'une loi exponentielle.

Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲