Nous allons étudier dans ce chapitre la notion de chaîne de Markov.
Cette notion permet d'étudier l'évolution de phenomènes dépendant du hasard de manière constante.
Exemples de graphes probabilistes à $N$ sommets
Premier exemple
Lors d'un travail de recherche, un étudiant lit différentes pages web.
Il passe d'une page à l'autre à partir des liens hypertexte.
Cet étudiant juge la page soit pertinente, soit non pertinente.
L'expérience acquise au cours de ce type de recherche permet de prévoir que si :
-
si une page est pertinente, la suivante a une probabilité égale à 0.6 d'être elle aussi pertinente,
-
si une page est non pertinente, la suivante a une probabilité égale à 0.9 d'être non pertinente.
On note $V_n$ l'événement "la $n$-ième page est pertinente" et $p_n$ sa probabilité.
On suppose que la première page est pertinente, c'est à dire que $p_1=1$.
-
Reproduire et compléter l'arbre de probabilités ci-dessous :
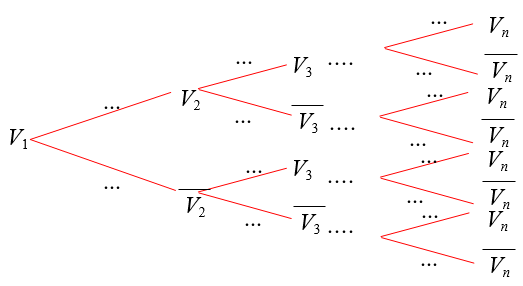
-
Plutôt que d'utiliser un tel arbre, vu la répétition de l'écriture de $V$ et de $\overline{V}$, on peut modéliser la situation par un graphe probabiliste comme celui ci-dessous.
Le reproduire et le compléter :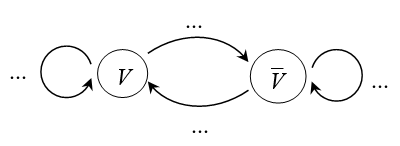
Ce type de schéma est appelé graphe probabiliste à 2 états.
-
On note $X_1$, $X_2$, ..., $X_n$, les variables aléatoires représentant les situations aux étapes successives de consultation des pages.
Les valeurs de ces variables sont soit $V$ (page pertinente), soit $\overline{V}$ (page non pertinente) et sont prises aux instants 1, 2, 3, 4, ....Reproduire et compléter la ligne ci-dessous afin d'obtenir une situation possible sur la consultation des quatre première page :
$X_1=...$ ; $X_2=...$ ; $X_3=...$ et $X_4=...$.
-
Un graphe est un ensemble de points appelés sommets associés un ensemble d’arêtes telles qu’à chaque arête sont associés deux sommets.
-
Un graphe probabiliste est un graphe orienté (les arêtes sont orientées et représentées par des flèches) et pondéré (les arêtes portent des valeurs) dans lequel :
-
il y a au plus une arête allant d’un sommet vers un autre ;
-
la somme des poids des arêtes partant d’un même sommet est égale à 1.
-
Le schéma suivant est un graphe probabiliste :
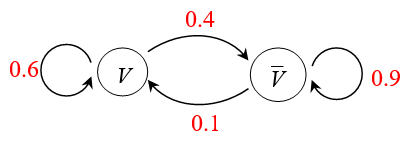
-
Les sommets du graphes sont $V$ et $\overline{V}$.
-
Les quatre arêtes sont orientées : $V->\overline{V}$, $V->V$, $\overline{V}->\overline{V}$ et $\overline{V}->V$.
-
Chaque arête possède un poids : 0.4 ; 0.6 ; 0.9 et 0.1.
-
La somme des poids des arêtes issues du sommet $V$ vaut 1 $(=0.4+0.6)$.
-
La somme des poids des arêtes issues du sommet $\overline{V}$ vaut 1 $(=0.9+0.1)$.
-
Quels sont les sommets du graphe ?
-
Déterminer les valeurs de $x$ et de $y$ pour que le graphe ci-dessous soit un graphe probabiliste.
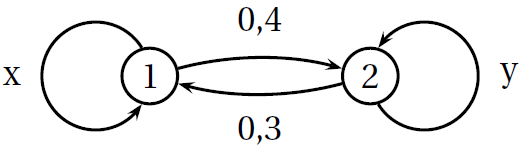
-
Pourquoi obtient-on bien ainsi un graphe probabiliste ?
On reprend l'exemple de l'exercice précédent.
On considère la suite de la pertinence des pages visitées.
Pour chaque page, il n'y a que deux possibilités :
-
$V$ : "page pertinente",
-
$\overline{V}$ : "page non pertinente".
Voici des exemples possibles de telle suite, sachant que l'on a supposé que la première page est forcément pertinente :
-
$(V,V,\overline{V},V,\overline{V},\overline{V},\overline{V},\overline{V},\overline{V},V,...)$
-
$(V,V,V,\overline{V},\overline{V},\overline{V},V,V,\overline{V},\overline{V},...)$
Nous avons supposé que la probabilité qu'une page soit pertinente ne dépend que de la pertinence ou non de la page précédente.
On peut voir cela d'une autre manière : lorsque l'on est sur une page, la pertinence de la page future ne dépend pas des pages passées, mais
seulement de celle actuelle.
Nous avons aussi supposé que les probabilités pour passer d'un état de pertinence à un autre sont indépendantes du nombre de pages déjà visitées.
On arrive ainsi la définition suivante compliquée :
Une chaîne de Markov est une suite $(X_n)$ de variables aléatoires modélisant l'évolution par étapes successives d'un système aléatoire comportant différents états telle que :
-
pour tout état $E_i$, l'événement ${X_{n+1}=E_i}$ ne dépend que de l'état de la variable aléatoire $X_n$ : le futur ne dépend que de l'instant présent.
-
la probabilité de passer de l'état $E_i$ à l'état $E_j$ ne dépend pas de $n$ : l'évolution est constante dans le temps.
À l'étape $n=0$, la probabilité de $X_0$ s'appelle la distribution initiale du système.
À l'étape $n$, la probabilité de $X_n$ s'appelle la distribution après $n$ transitions.
On reprend l'exemple de l'exercice précédent.
Il y a deux états possibles :
-
$V$ : la page est pertinente,
-
$\overline{V}$ : la page n'est pas pertinente.
La suite $(X_1, X_2, X_3, X_4, X_5, X_6, X_7, X_8, X_9, X_{10}, X_{11}, X_{12}, ...)$ est une
chaîne de Markov.
$(V,V,\overline{V},V,\overline{V},\overline{V},V,\overline{V},\overline{V},\overline{V},V,V,...)$ représente un état
possible de cette chaîne de Markov, état signifiant, en reprenant le thème du premier exercice de ce chapitre, que :
-
le premier site est pertinent ($V$),
-
le deuxième site est pertinent ($V$),
-
le troisième site n'est pas pertinent ($\overline{V}$),
-
le quatrième site est pertinent ($V$),
-
le cinquième site n'est pas pertinent ($\overline{V}$),
-
le sixième site n'est pas pertinent ($\overline{V}$),
-
le septième site est pertinent ($V$),
-
le huitième site n'est pas pertinent ($\overline{V}$),
-
le neuvième site n'est pas pertinent ($\overline{V}$),
-
le dixième site n'est pas pertinent ($\overline{V}$),
-
le onzième site est pertinent ($V$),
-
le douzième site est pertinent ($V$),
-
...
La distribution initiale du système est donnée par la matrice ligne $(P(X_1=V) \ \ P(X_1=\overline{V}))$, soit $(1 \ \ 0)$ puisque l'on est certain que le premier site trouvé est pertinent.
Second exemple
Elsa décide de créer son blog. Celui-ci comporte quatre pages numérotées 1, 2, 3 et 4.
Toutes ces pages sont reliées entre elles par un système de liens hypertextes.
On peut passer :
-
de la page 1 aux pages 2 et 4,
-
de la page 2 aux pages 3 et 4,
-
de la page 3 à la page 1,
-
de la page 4 aux pages 2 et 3.
On veut modéliser ce problème par un graphe orienté.
-
Quels sont ici les sommets de graphe orienté ?
-
Construire un graphe orienté représentant le blog avec ses liens hypertextes.
-
On suppose que les amis d'Elsa qui viennent visiter son blog naviguent de façon aléatoire et sans se préoccuper des pages précédemment visitées.
Compléter le graphe orienté précédent afin de le transformer en un graphe probabiliste. -
Déterminer la distribution initiale $P_0=(P(X_0=1)\ \ P(X_0=2)\ \ P(X_0=3)\ \ P(X_0=4))$ du système.
Matrice de transition
Les arêtes d'un graphe probabiliste sont pondérées par les probabilités conditionnelles : l’arête allant du sommet $i$ au sommet $j$ porte la probabilité $p_{ij}$, appelée probabilité de transition de l’état $i$ à l’état $j$.
On reprend le premier exemple de ce cours.
On y avait obtenu le graphe suivant : 
En notant 1 le sommet $V$ et 2 le sommet $\overline{V}$, on obtient les probabilités de
transition suivantes :
-
$p_{11}=0.6$ : probablité de passer de l'état $V$ à l'état $V$,
-
$p_{12}=0.4$ : probablité de passer de l'état $V$ à l'état $\overline{V}$,
-
$p_{21}=0.1$ : probablité de passer de l'état $\overline{V}$ à l'état $V$,
-
$p_{22}=0.9$ : probablité de passer de l'état $\overline{V}$ à l'état $\overline{V}$.
La matrice $T=(p_{ij})$ dont le coefficient $p_{ij}$ de la $i$-ème et de la $j$-ème colonne est la probabilité de transition de l’état $i$ vers l’état $j$ est appelée matrice de transition.
On reprend encore le premier exemple de ce cours.
On y avait obtenu le graphe suivant : 
En notant 1 le sommet $V$ et 2 le sommet $\overline{V}$, on obtient, à l'aide des probabilités de transition
calculées précédemment, la matrice de
transition suivante : $\begin{pmatrix} 0.6&0.4 \\ 0.1&0.9 \end{pmatrix}$
Plus généralement, toute matrice de transition vérifie les propriétés suivantes :
La matrice de transition $T=(p_{ij})$ associée à une chaîne de Markov à $N$ sommets vérifie :
-
$T$ est une matrice carrée d’ordre $N$ ($N$ lignes et $N$ colonnes) ;
-
tous ses coefficients (les probabilités de transition) sont comprises entre 0 et 1 : $0\le p_{ij}\le 1$.
-
La somme des termes appartenant à la même ligne d'une matrice de transistion vaut toujours 1.
-
Recopier et compléter la matrice de transition $T$ ci-dessous.
$T=\begin{pmatrix} ...&0.6&0.1 \\ 1&...&...\\ ...&0.3&0.5 \end{pmatrix}$ -
En notant les sommets dans cet ordre $A$, $B$, $C$, proposer un graphe probabiliste qui correspond à cette matrice de transition.
On reprend le le second exemple du cours étudiant le blog d'Elsa.
Déterminer la matrice de transition associée à la navigation aléatoire sur ce blog en
s'appuyant sur le graphe orienté dajà obtenu.
On considère un pays subissant une épidémie ; ses habitants peuvent être dans trois états :
-
$S$ : "sain",
-
$M$ : "malade",
-
$I$ : "immunisé".
Des études montrent que, d'un mois à l'autre, chaque habitant peut voir son état changer selon les règles suivantes :
-
s'il est sain, il le reste avec une probabilité de 0.8 et tombe malade avec une probabilité de 0.2,
-
s'il est malade, il le reste avec une probabilité de 0.1 et devient sinon immunisé,
-
s'il est immunisé, il le reste avec une probabilité de 0.7 et devient sain avec une probabilité de 0.3.
Au début de l'épidémie, 2% de la population est malade et 1% est immunisée.
-
Quel est l'ensemble des états possibles ?
-
Justifier que l'évolution de l'état d'un individu mois par mois peut être modélisé par une chaîne de Markov.
-
Proposer le graphe probabiliste associé à cette chaîne de Markov.
-
Proposer la matrice de transition $T$ associée (en conservant l'ordre alphabétique).
-
Déterminer la distribution initiale $P_0=(P(X_0=I)\ \ P(X_0=M)\ \ P(X_0=S))$ du système.
-
Que représente concrètement les coefficients obtenus par le calcul du produit matriciel $ P_0 T$ ?
Évolution d'une chaîne de Markov
On considère dans cette partie une chaine de Markov $(X_n)$ dont la matrice de transition est notée $T$.
On note $P_n$ la distribution après $n$ transitions écrite sous forme d'une matrice ligne ayant autant de colonne que d'états différents
et telle que le terme de la $j$-ième colonne est la probabilité qu'à l'étape $n$ la variable $X_n$ soit égale à l'état $E_j$.
Ainsi, pour tout entier naturel non nul $n$, on note : $P_n=\begin{pmatrix} P(X_n=E_1)&...&P(X_n=E_j)&...&P(X_n=E_k) \end{pmatrix}$ si $k$ est
le nombre d'états.
Pour tout entier naturel non nul $n$, $P_{n+1}=P_n\times T$.
On retrouve une relation comme celle définissant une suite géométrique.
Vous n'êtes dès lors par surpris.e.s de découvrir la propriété suivante :
Pour tout état $E_i$ et $E_j$ et pour tout entier naturel $n\ge 1$, le coefficient de la ligne $i$ et de la colonne $j$ de la matrice $T^n$ est la probabilité de passer de l'état $E_i$ à celui $E_j$ en $n$ transitions.
Autrement dit :
Pour tout entier naturel $n$ non nul, $P_n=P_0 T^n$.
Un internaute navigue sur un mini Web composé de trois pages. Ces pages possèdent des liens hypertextes qui
permettent de passer de certaines à d'autres par simple clic.
Voici la structure obtenue avec ces liens :
-
la page A contient 3 liens : 2 menant à la page B et 1 à la page C,
-
la page B contient 4 liens : 2 vers la page A, 1 vers elle-même et 1 vers la page C,
-
la page C contient 2 liens : 1 vers la page A et 1 vers la page B.
-
Représenter la situation par un graphe probabiliste.
-
Déterminer la matrice de transition $T$ associée à ce graphe probabiliste.
-
On admet que $T^2=\begin{pmatrix} \frac{1}{2}&\frac{1}{3}&\frac{1}{6}\\ \frac{1}{4}&\frac{25}{48}&\frac{11}{48} \\ \frac{1}{4}&\frac{11}{24}&\frac{7}{24}\end{pmatrix}$.
Quelle est la signification concrète de $T^2_{23}=\frac{11}{48}$ ?
-
L'internaute est sur la page A et effectue 10 clics.
Sur quelle page a-t-il le plus de chance d'arriver ? Justifier.
Étude asymptotique
Soit $(X_n)$ une chaîne de Markov à $N$ états de matrice de transition $T$.
S'il existe un entier naturel $n$ tel que la matrice $T^n$ ne contient pas de 0 alors la suite des distributions $(P_n)$
converge vers l'unique matrice $\pi$ vérifiant $\pi T=\pi$ et telle que tous ses coefficients sont compris entre 0 et 1
et telle que leur somme donne 1.
De plus, cette limite $\pi$ ne dépend pas de la distribution initiale $P_0$.
Dire que la matrice $T^n$ ne contient pas de 0 signifie que l'on peut passer de n'importe quel état à n'importe quel autre en exactement $n$ étapes.
En particulier pour $n=1$, si la matrice de transition $T$ ne contient pas de 0 alors la suite $(P_n)$ converge vers une telle matrice $\pi$ vérifiant $\pi T=\pi$.
En cas d'existence, une telle distribution $\pi$ est appelée la distribution invariante ou état stable de la chaîne de Markov.
On reprend l'exercice sur le surf dans un mini Web avec la notation $T$ pour sa matrice de transition.
-
Soit $P$ la matrice définie par $P=\begin{pmatrix} \frac{1}{3}&\frac{4}{9}&\frac{2}{9}\end{pmatrix}$.
Calculer le produit matriciel $P T$. -
Que pouvez-vous en déduire ?
-
Calculer sur Xcas $P T^{100}$ et $P T^{1000}$.
Que pouvez-vous vérifier alors ? -
On considère un internaute qui navigue sur ce mini Web. Il part d'une page quelconque.
Sur quelle page a-t-il le plus de chance de se touver à très long terme ?
Sur quelle page a-t-il le moins de chance de se touver à très long terme ?
L'algorithme de PageRank® qui a fait la fortune du groupe Google est une amélioration de la démarche vue dans cet exercice.
Un ordinateur a été programmé pour afficher une succession de lettres. Ces lettres sont soient des
consonnes (C), soit des voyelles (V).
On admet que le programme conduit à cette règle constante :
-
si une lettre est une voyelle, la suivante est encore une voyelle dans 50% cas.
-
si une lettre est une consonne, la suivante sera une voyelle avec une probabilité de 0.8.
-
Représenter la situation par un graphe probabiliste.
-
Déterminer la matrice de transition associée à ce graphe probabiliste.
-
On suppose que la première lettre est une voyelle.
Déterminer la probabilité que la dixième lettre soit une consonne. -
On pose $\pi=\begin{pmatrix} x&y \end{pmatrix}$.
Justifier que $\pi$ est la distribution invariante du système si, et seulement si, $(x;y)$ est solution du système : $\left \{ \begin{array}{rcl} 0.8x-0.5y&=&0 \\ x+y&=&1 \end{array} \right.$ -
En déduire la distribution invariante de ce système.
-
Interpréter le résultat.
Exercices
Utilisation d'un graphe probabiliste
Voici le graphe probabiliste représentant un processus aléatoire :
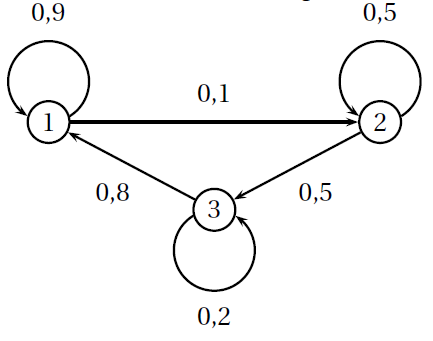
-
Déterminer la matrice de transition associée à cette chaîne (en considérant les états par ordre croissant).
-
La marche aléatoire part du sommet 1.
Quelle est la probabilité d’être sur le sommet 3 en deux étapes ? En trois étapes ? -
La marche aléatoire part du sommet 2. Quelle est la probabilité d’être sur le sommet 3 en deux étapes ? En trois étapes ?
-
Déterminer par le calcul l’état stable de cette chaîne.
-
Au bout d’un très grand nombre d’étapes, sur quel sommet a-t-on le plus de chance de se trouver ?
$(X_n)$ est une chaîne de Markov à valeurs dans ${1,2,3,4}$ de matrice de transition :
$T=\begin{pmatrix} ...&0&\dfrac{1}{2}&\dfrac{1}{3}\\\dfrac{1}{2}&0&0&...\\...&...&1&...\\ \dfrac{1}{4}&\dfrac{3}{4}&...&...\end{pmatrix}$
-
Recopier et compléter la matrice $T$ pour en faire une matrice de transition.
-
Représenter le graphe probabiliste associé à cette matrice de transition.
Voici un graphe :
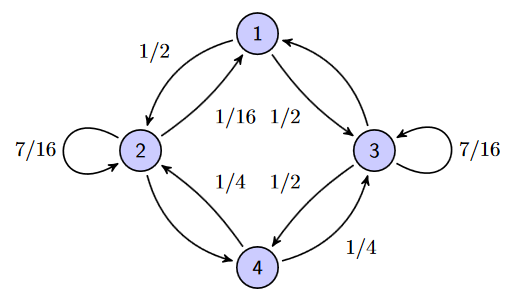
-
Recopier et compléter ce graphe avec les probabiltés manquantes et en rajoutant un arc allant de 4 vers 4 afin d'obtenir un graphe probabiliste.
-
Déterminer la matrice de transition $T$ associée à ce graphe probabiliste.
-
Déterminer $T^2$.
-
Déterminer la probabilité de passer du sommet 1 au sommet 4 en deux déplacements.
-
Peut-on atteindre n'importe quel sommet à partir de n'importe qu'elle autre sommet en deux déplacements ? Pourquoi ?
-
Quelle est la valeur de $P_{(X_2=3)}(X_4=2)$ ?
-
Déterminer, à l'aide de Xcas, $P_{(X_0=1)}(X_4=2)$.
-
Déterminer $P_{(X_0=3)}(X_{100}=3)$.
Modéliser des problèmes concrets
Deux joueurs A et B s'affrontent dans une partie de tennis.
Chaque point joué est gagné par le joueur A avec une probabilité de $\dfrac{3}{5}$, sinon il est gagné par B.
On suppose les points indépendants.
Initialement, les deux joueurs sont à égalité. Pour gagner la partie, un joueur doit obtenir une avance
de deux points sur son opposant.
-
Modéliser le jeu par une chaîne de Markov avec 5 les états suivants : Égalité, Avantage A, Avantage B, A gagne, et B gagne.
-
Donner la matrice de transition de cette chaîne.
-
Calculer la probabilité que A gagne, si les joueurs sont initialement à égalité.
Un contrat d'assurance automobile comporte trois tarifs de cotisation annuelle : Bas, Intermédiaire, Haut.
-
La première année, l'assuré paye le tarif intermédiaire.
-
S'il n'a pas été responsable d'un accident pendant une année, il passe au tarif inférieur l'année suivante (s’il est déjà au tarif bas, il y reste).
-
S'il a été responsable d'un accident au cours d'une année, il passe au tarif supérieur l'année suivante (s’il est déjà au tarif haut, il y reste).
La compagnie d’assurance estime à 10% la probabilité qu'un assuré pris au hasard soit responsable d'un accident
au cours d'une année.
Quelle sera à long terme la répartition des assurés entre les trois catégories de tarif ?
Partie A : étude générale d'un graphe
Voici un graphe probabiliste :
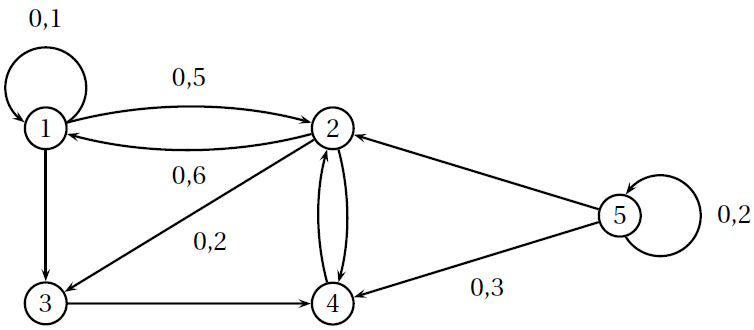
-
Peut-on atteindre le sommet 1 du graphe en deux étapes, en partant de n’importe quel sommet ?
-
Recopier et compléter le graphe précédent avec les probabilités manquantes.
-
Donner la matrice de transition $T$ associée à la chaîne dans l’ordre croissant des états.
-
-
Calculer $T^2$.
-
En déduire la valeur de la probabilité $P_{(X_0=1)}(X_2=1)$.
-
Déterminer la valeur de la probabilité $P_{(X_0=3)}(X_2=3)$.
-
Déterminer la valeur de la probabilité $P_{(X_0=2)}(X_2=4)$.
-
-
Justifier, en utilisant la matrice $T^2$, la réponse donnée à la question 1.
-
Déterminer la valeur de la probabilité $P_{(X_2=4)}(X_7=4)$ en explicitant la démarche.
Partie B : étude générale d'un graphe
Latifa décide de créer son blog Internet. Celui-ci comporte cinq pages numérotées (1), (2), (3), (4) et (5).
La page (5) n'est accessible que par elle en tant qu'administratrice.
Toutes les pages sont reliées entre elles par un système de lien hypertextes.
L’organisation de ces liens peut-être représentée par le graphe orienté de la partie A.
Latifa décide alors d’inviter ses amis pour leur faire découvrir son blog et ainsi mesurer la pertinence des liens mis
entre ses quatre pages (1), (2), (3) et (4).
Chacun leur tour, les amis vont s’installer sur l’ordinateur et visiter les différentes pages du site en cliquant
sur les liens hypertextes de façon aléatoire et sans se préoccuper de leurs parcours antérieurs.
Lorsqu’un ami décide d’arrêter la visite, il laisse la place à un autre qui reprend l’exploration sur la page en cours.
-
On note $X_n$ la variable aléatoire qui représente la page ouverte après $n$ clics ; $X_0$ ; $X_1$ ; $X_2$ ; ... forme une chaîne de Markov.
On note $Y_n$ la matrice ligne représentant la loi de $X_n$, c'est-à-dire la distribution de la chaîne de Markov après $n$ transitions : $Y_n=(P(X_n=1)\ \ P(X_n=2)\ \ P(X_n=3)\ \ P(X_n=4))$.-
Déterminer la matrice de transition $T$ associée au graphe pondéré en omettant le site (5).
-
Exprimer $Y_n$ en fonction de $Y_0$, $n$ et $T$.
-
On suppose qu'un ami commence par la page 2. Que vaut $Y_0$ ?
-
-
-
Justifier que $S=\left(\dfrac{5}{21}\ \ \dfrac{5}{14}\ \ \dfrac{1}{6}\ \ \dfrac{5}{21}\right)$ est un état stable.
-
Comparer les coefficients de $S$ et de $Y_{100}$.
-
Quel classement peut-on associer aux quatre pages (1), (2), (3) et (4) du blog de Latifa ?
-
-
On admet que l'espérance du temps de premier retour à la page $i$ est donné par $\dfrac{1}{S_i}$, où $S_i$ est le coefficient de la $i$ème ligne de la matrice donnant l'état stable $S$.
-
Déterminer le nombre moyen de clics pour revenir à la page 3.
-
Déterminer le nombre moyen de clics pour revenir à la page 2.
-
Vous voilà transporté.e.s dans un voyage temporel au XIVe siècle, dans le château de Poitiers.
Vous êtes la sentinelle faisant sa ronde sur le rempart de ce château triangulaire.
Il est flanqué d’une tour à chacun des trois angles : Est, Nord, Sud.
Vous avez connu plus passionnant. À chaque angle, pour tromper l’ennui certain et l’ennemi éventuel, vous jetez une
pièce de monnaie (de l'époque).
-
Pile, vous continuez votre ronde dans le même sens ;
-
Face, vous repartez en sens inverse.
Votre chef vous impose de commencer par la tour Est.
Pouvez-vous avec votre stratégie assurer une surveillance
identique dans toutes les directions ?
Dans chaque paquet de lessive "homo saviens", on trouve une figurine de collection.
La série complète comporte 4 figurines.
-
Représenter le processus par un graphe probabiliste où les sommets correspondent au nombre de figurines différentes possédées.
-
Établir la matrice de transition associée.
-
Déterminer la probabilité d'obtenir $k$ figurines différentes, où $k\in\{1;2;3;4\}$, avec 4 paquets de lessive achetés.
-
Que peut-on dire de ces probabilités si le nombre de paquets de lessive achetés devient très grand ?
-
On note $T$ la variable aléatoire donnant le nombre de paquets qu'il faut acheter pour acheter la collection complète.
On note $e_{12}$ le nombre moyen de paquets qu'il faut acheter pour passer de 1 figurine à 2 figurines de collection, $e_{23}$ le nombre moyen d'achats pour passer de 2 à 3 figurines et $e_{34}$ celui pour obtenir la dernière figurine.
On admet que $e_{12}$, $e_{23}$ et $e_{34}$ vérifient les équations suivantes :-
$e_{12}=1+p_{11}\times e_{12}$,
-
$e_{23}=1+p_{22}\times e_{23}$,
-
$e_{34}=1+p_{33}\times e_{34}$,
où $p_{ii}$ correspond au coefficient de la $i$ème ligne et de la $i$ème colonne de la matrice de transition.
Déterminer le nombre moyen de paquets qu'il faut acheter pour obtenir la collection complète.
-
Dans chaque paquet de chocolat "Troubléronronne", on trouve une image de collection.
La série complète comporte 6 images.
-
Représenter le processus par une chaîne de Markov où les sommets correspondent au nombre d’image différentes possédées.
-
Établir la matrice de transition correspondante.
-
Déterminer la probabilité d'obtenir $k$ images différentes, où $k\in\{1;2;3;4;5;6\}$, avec 6 paquets de chocolat achetés.
-
Déterminer la probabilité d’avoir 5 images différentes si on achète 10 paquets de chocolat.
-
Que peut-on dire de ces probabilités si le nombre de paquets de chocolat achetés devient très grand ?
Chaque semaine, Anna achète une tablette de chocolat Cébon.
Chaque tablette contient un autocollant représentant soit une étoile, soit un cœur, soit un trèfle à quatre feuilles.
Anna les collectionne pour décorer son journal intime.
-
En supposant les trois motifs équirépartis entre les tablettes, combien de tablettes suffit-il d’acheter pour être sûr à plus de 95 % d’avoir les trois types de dessin ?
-
L'entreprise décide de réaliser une nouvelle collection de 6 nouveaux autocollants. Combien de semaines seront nécessaire pour être sûr à plus de 99 % d’avoir les six types de dessin ?
Une souris est lancée dans le labyrinthe suivant. Elle commence en A où se trouve sa cage.
En B il y a un morceau de fromage, en C un chat affamé. 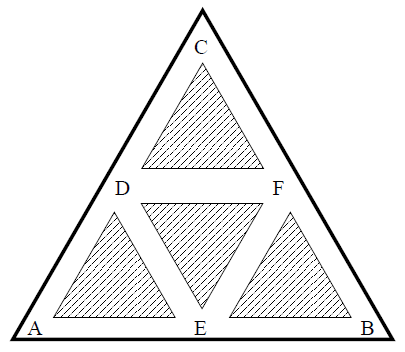
La souris parcourt les couloirs en choisissant au hasard parmi les couloirs offerts à chaque nouvelle intersection.
Elle met une seconde en moyenne entre deux intersections.
-
Déterminer la matrice $P$ de transition associée à ce jeu.
-
Quelle est l'issue de ce jeu cruel ?
-
Quelle est la probabilité que la souris se fasse manger le ventre plein ?
-
Quelle est la probabilité que la souris revoit sa chère cage avant de se faire manger ?
-
Quelle est la probabilité que la souris n’ait pas revu sa cage et se fasse manger le ventre vide ?
-
On note $e_{i3}$ le nombre moyen de déplacements pour passer du sommet $i$ au sommet $3$, correspondant à C.
On note $E=(e_{13}\ \ e_{23}\ \ e_{33}\ \ e_{43}\ \ e_{53}\ \ e_{63})$, $U=(1\ \ 1\ \ 1\ \ 1\ \ 1\ \ 1)$ et $F$ la matrice ligne $\left(0\ \ 0\ \ 1\ \ \dfrac{1}{4}\ \ 0\dfrac{1}{4}\right)$ qui correspond à la troisième colonne de la matrice de transition $P$.
On admet que $E$ vérifie $E=U+EP-e_{33}F$.
-
Déterminer la matrice $E$.
-
Combien de temps dure en moyenne ce jeu cruel ?
-
On place un rat dans la case 1 du labyrinthe suivant : 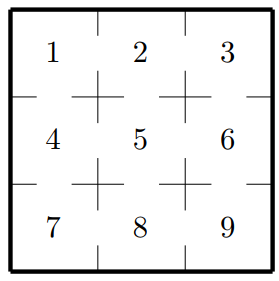
A chaque fois qu’il se retrouve dans une des 8 premières cases, le rat choisit une des portes disponibles au hasard,
et indépendamment de ses choix précédents. La case 9 correspond à une sortie.
Soit $X_n$ le numéro de la $n$-ième case visitée par le rat.
-
Pourquoi $(X_n)$ est une chaîne de Markov ?
-
Donner la matrice de transition $T$ associée à la situation.
-
Quelle est la probabilité que le rat soit sortie en moins de 7 déplacements ?
-
Un morceau de fromage est placé dans la case 5.
On admet que le rat ne peut pas repérer, par odeur ou autre, la présence de ce fromage à partir des cases voisines.
Quelle est la probabilité que le rat sorte du labyrinthe le ventre plein ? -
Quelle est la probabilité que le rat revoit sa case initiale avant de sortir ?
-
Quelle est la probabilité que le rat sorte du labyrinthe le ventre vide et sans être repassé par la case départ ?
-
On note $e_{i9}$ le nombre moyen de déplacements pour passer du sommet $i$ au sommet 9, correspondant à la sortie.
On note $E=(e_{19}\ \ e_{29}\ \ e_{39}\ \ e_{49}\ \ e_{59}\ \ e_{69}\ \ e_{79}\ \ e_{89})$, $U=(1\ \ 1\ \ 1\ \ 1\ \ 1\ \ 1\ \ 1\ \ 1)$ et $Q$ la matrice carrée 8X8 correspondant à la matrice de transition $T$ à laquelle ont été enlevée la 9ème ligne et la 9ème colonne.
On admet que $E$ vérifie $E=U+EQ.$.-
Déterminer la matrice $E$.
-
Si le rat part de la case 1 et franchit une case toutes les secondes, combien de temps mettra-t-il en moyenne pour sortir du labyrinthe ?
-
Si le rat part de la case 1 et franchit une case toutes les secondes, combien de temps mettra-t-il en moyenne à atteindre le fromage qui se trouve au centre ?
-
Bilbo le hobbit est perdu dans les cavernes des orques, où règne une obscurité totale.
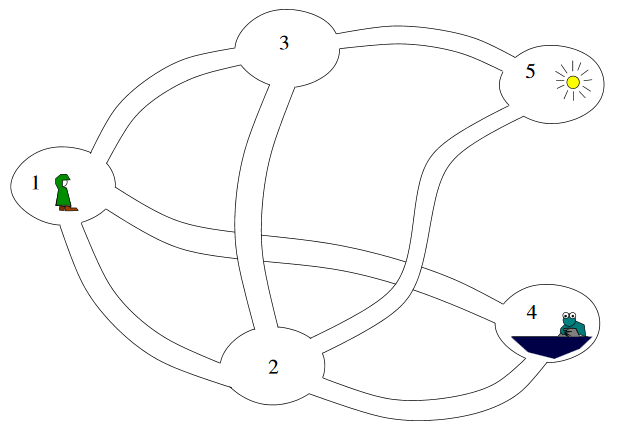
Partant de la caverne 1, il choisit de manière équiprobable l'une des galeries partant de cette caverne
et continue de cette manière jusqu'à ce qu'il aboutisse soit à la caverne Gollum (caverne 4), soit à l'air libre (numéro 5).
-
Modéliser l'itinéraire de Bilbo le Hobbit par un graphe probabiliste.
-
Modéliser l'itinéraire de Bilbo le Hobbit par une matrice de transition.
-
Partant de 1, quelle est la probabilité que Bilbo trouve la sortie plutôt que de déboucher sur la caverne de Gollum ?
Pertinence de pages web
Éric décide de créer son blog Internet. Celui-ci comporte quatre pages numérotées (1), (2), (3) et (4).
Toutes ces pages sont reliées entre elles par un système de lien hypertextes.
L’organisation de ces liens peut être représentée par le graphe orienté suivant :
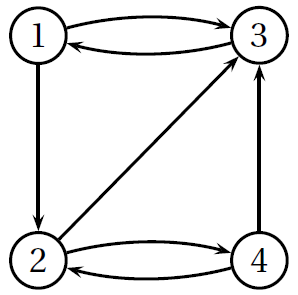
Éric décide alors d’inviter ses amis pour leur faire découvrir son blog et ainsi mesurer la pertinence des liens mis entre
ses quatre pages.
Chacun leur tour, les amis vont s’installer sur l’ordinateur et visiter les différentes pages du site en
cliquant sur les liens hypertextes de façon aléatoire et sans se préoccuper de leurs parcours antérieurs.
Lorsqu’un ami décide d’arrêter la visite, il laisse la place à un autre qui reprend l’exploration sur la page en cours.
-
-
Philippe entre sur le blog par la page (4).
Peut-il revenir à cette page en deux clics ? 3 clics ? 4 clics ? -
Au vu du schéma ci-dessus, peut-on prévoir la page qui sera la moins visitée ?
-
-
On note $X_n$ la variable aléatoire qui représente la page ouverte après $n$ clics ; $(X_0 ; X_1 ; X_2 ; ...)$ forme une chaîne de Markov.
On note $Y_n$ la matrice ligne représentant la distribution après $n$ transitions.
-
Recopier et compléter le graphe orienté ci-dessus pour en faire un graphe probabiliste modélisant la situation.
-
En déduire la matrice de transition $T$ associée à ce graphe probabiliste.
-
Exprimer $Y_n$ en fonction de $Y_0$, $n$ et $T$.
-
-
-
Calculer $T^7$.
-
Calculer $Y_7$ lorsque $Y_0=(1\ \ 0\ \ 0\ \ 0)$, puis lorsque $Y_0=(0\ \ 1\ \ 0\ \ 0)$, puis lorsque $Y_0=(0\ \ 0\ \ 1\ \ 0)$, enfin lorsque $Y_0=(0\ \ 0\ \ 0\ \ 1)$.
-
La première page explorée joue-t-elle un rôle dans la probabilité de visite des autres pages ?
-
Même question pour $T^{20}$ et $T^{100}$.
-
Que peut-on alors conjecturer de l’importance du choix de la première page ?
-
-
-
Montrer que l’état probabiliste $S = \left(\dfrac{1}{3}\ \ \dfrac{2}{9}\ \ \dfrac{1}{3}\ \ \dfrac{1}{9}\right)$ est un état stable.
-
Comparer les coefficients des lignes de $T^{20}$ (respectivement $T^{100}$) à ceux de $S$.
-
Justifier que quel que soit l’état initial $Y_0$, $Y_n$ semble se stabiliser, quand $n$ devient très grand, autour de $S$.
-
-
Quel classement peut attribuer Éric aux quatre pages de son blog ?
Un robot Google parcourt Internet de la manière suivante : quand il est sur une page web, il regarde tous les liens Internet présents sur la page et choisit un de ces liens de façon aléatoire.
-
Sur la page 1, on trouve un lien vers les pages 2 et 5.
-
Sur la page 2, on trouve un lien vers les pages 3 et 5.
-
Sur la page 3, on trouve un lien vers les pages 4 et 6.
-
Sur la page 4, on trouve un lien vers les pages 6 et 1.
-
Sur la page 5, on trouve un lien vers la page 4.
-
Sur la page 6, on trouve un lien vers la page 1.
-
Représenter la situation par un graphe probabiliste.
-
Donner la matrice de transition associé à cette situation.
-
Le graphe probabiliste admet-il un état stable ?
-
Classer par ordre décroissant la pertinence de ces six pages.
Voici un mini web à quatre sites dont voici la modélisation par un graphe orienté :
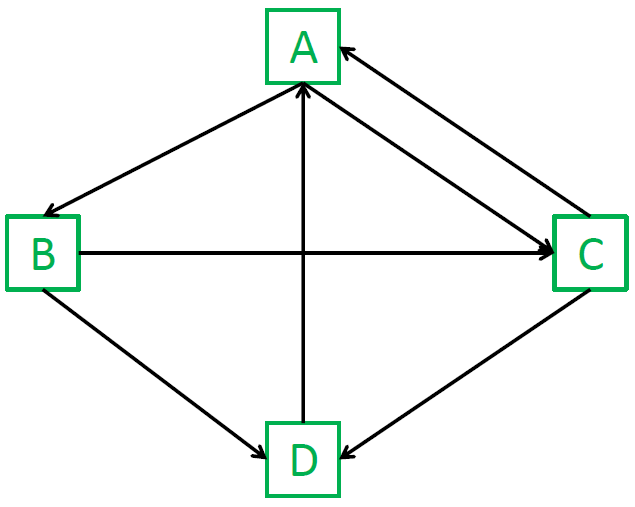
Imaginons un internaute qui « surfe » au hasard. Quand il est sur une page :
-
Soit, avec une probabilité $1-p$, il clique au hasard sur l’un des liens disponibles depuis cette page.
-
Soit, avec une probabilité $p$, il choisit une page au hasard dans l’ensemble du réseau.
-
En prenant $p=0.16$, transformer le graphe orienté initial en graphe probabiliste.
-
Déterminer la matrice de transition modélisant le surf sur ce mini web.
-
Classer ces quatre sites par ordre de pertinence.
Le réseau Internet peut être représenté comme un gigantesque graphe (non probabiliste),
dont les $N$ sommets sont les pages, et les flèches les liens qui pointent d’une page à une autre.
Un moteur de recherche, pour être utile, doit classer les pages par ordre de pertinence.
Comment mesurer la pertinence d’une page ?
L’algorithme PageRank utilisé par Google utilise pour cela une méthode probabiliste.
Imaginons un internaute qui « surfe » au hasard. Quand il est sur une page :
-
Soit, avec une probabilité $1-p$, il clique au hasard sur l’un des liens disponibles depuis cette page.
-
Soit, avec une probabilité $p$, il choisit une page au hasard dans l’ensemble du réseau.
On considère ici un mini-web à 4 pages, représenté par le graphe orienté suivant avec $p=0.25$ :

-
Déterminer le graphe probabiliste associé à ce mini-web.
-
Déterminer la matrice de transition modélisant le surf sur ce mini web.
-
Déterminer l’état stable de ce graphe probabiliste.
-
Classer ces quatre sites par ordre de pertinence.
Voici un mini web à quatre sites A, B, C et D dont voici la modélisation par un graphe :
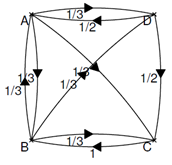
Partie A : sans saut aléatoire
-
Déterminer la matrice de transition modélisant le surf sur ce mini web.
-
Classer ces quatre sites par ordre de pertinence. Expliciter la démarche mise en œuvre.
Partie B : avec saut aléatoire
Imaginons un internaute qui « surfe » au hasard. Quand il est sur une page :
-
Soit, avec une probabilité $\dfrac{5}{6}$, il clique au hasard sur l’un des liens disponibles depuis cette page.
-
Soit, avec une probabilité $\dfrac{1}{6}$, il choisit une page au hasard dans l’ensemble du réseau.
-
Déterminer la matrice de transition modélisant le surf sur ce mini web.
-
Classer ces quatre sites par ordre de pertinence. Expliciter la démarche mise en œuvre.
-
Que constatez-vous quant à l'effet du saut sur le classement ?
Liens avec d'autres chapitres
Une salle de spectacle propose deux types d’abonnements pour une année :
-
l’abonnement A donne droit à six spectacles,
-
l’abonnement B donne droit à trois spectacles.
On considère le groupe des 3000 personnes qui s’abonnent tous les ans. Pour $n$ entier naturel, on note :
-
$a_n$ la probabilité qu’une personne ait choisi un abonnement A pendant l’année $n$ ;
-
$b_n$ la probabilité qu’une personne ait choisi un abonnement B pendant l’année $n$ ;
-
$P_n$ la matrice ligne $(a_n\ \ b_n)$ traduisant l’état probabiliste à l’année $n$.
Tous les ans, 80% des personnes qui ont choisi l’abonnement A et 50% des personnes qui ont choisi l’abonnement B conservent leur choix d’abonnement l’année suivante. Les autres personnes changent d’abonnement.
-
On suppose que l’année 0, 2000 personnes ont choisi l’abonnement A et 1000 ont choisi l’abonnement B. Déterminer l’état initial $P_0=(a_0\ \ b_0)$.
-
-
On modélise ce problème par une chaîne de Markov.
Donner son graphe et sa matrice de transition. -
En déduire le nombre d’abonnés pour chaque type d’abonnement à l’année 1.
-
-
On note $S=(x\ \ y)$ un état stable avec $x$, $y$ deux réels positifs.
-
Justifier que $x$ et $y$ vérifient l’équation $x=0.8x+0.5y$.
-
Déterminer $x$ et $y$.
-
En déduire la limite de la suite $(a_n)$ quand $n$ tend vers $+\infty$.
-
Interpréter ce résultat en termes de nombre d’abonnement de type A.
-
On a divisé une population en deux catégories : "fumeurs", "non fumeurs".
Une étude statistique a permis de constater que d'une génération à l'autre :
-
60% des descendants des fumeurs sont des fumeurs,
-
10 % des descendants de non-fumeurs sont des fumeurs.
On suppose que le taux de fécondité des fumeurs est le même que celui des non-fumeurs.
On désigne par $f_n$ la proportion de fumeurs à la génération de rang $n$ et $g_n=1-f_n$ la proportion de non-fumeurs à
la génération de rang $n$, $n$ est un entier naturel. On note $P_n=(f_n\ \ g_n)$.
On considère qu'à la génération de rang 0, il y a autant de fumeurs que de non-fumeurs.
-
Traduire les données de l'énoncé par un graphe probabiliste.
-
Déterminer la matrice de transition $M$ telle que $P_{n+1}=P_nM$.
-
Déterminer le pourcentage de fumeurs à la génération 2.
-
Déterminer l'état stable $S=(f\ \ g)$ tel que $S=SM$.
Interpréter concrètement cet état stable. -
Justifier que pour tout entier naturel $n$ : $f_{n+1}=0.5f_n+0.1$.
-
On pose pour tout entier naturel $n$ : $u_n=f_n-0.2$.
-
Montrer que $u_n$ est une suite géométrique de raison et de premier terme à préciser.
-
En déduire l'expression de $u_n$ en fonction de $n$.
-
En déduire que $f_n=0.3\times 0.5^n+0.2$.
-
Déterminer la limite de la suite $(f_n)$ lorsque $n$ tend vers $+\infty$.
Interpréter ce résultat.
-
-
-
Déterminer la transformée en Z, $(Zf)(z)$, de la suite causale $(f_n e(n))$.
-
Retrouver la limite de la suite $(f_n)$ lorsque $n$ tend vers $+\infty$.
-
Demander le programme !
-
Le vocabulaire sur les graphes (sommet, arêtes, poids).
-
La notion de chaîne de Markov.
-
La notion de matrice de transition formée de probabilité de transition.
-
La notion de pertinence d'une page web.
-
Savoir modéliser un processus aléatoire grâce à un graphe probabiliste.
-
Savoir écrire la matrice de transition associée à un graphe probabiliste.
-
Savoir calculer une probabilité à partir d'un graphe probabiliste.
-
Savoir calculer une probabilité à partir d'une matrice de transition.
-
Savoir déterminer le comportement asymptotique d'un processus aléatoire.
-
Savoir estimer une durée moyenne issue d'un processus aléatoire.
-
Savoir classer un mini-web par ordre de pertinence des pages (avec ou sans sauts aléatoires).

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International