La transformée en $Z$ est très utile pour étudier les signaux numériques, des signaux analogiques échantillonnés ainsi que des filtres numériques.

Exemple concret : étude d'un filtre numérique particulier

Un régulateur numérique traite des informations échantillonnées-bloquées avec une période d’échantillonnage $T_e$.
On appelle $x_n$ la série d’échantillons arrivant sur l’entrée du régulateur.
En sortie, il fournit une série d’échantillons $y_n$, également échantillonnés, qui commandent le processus.

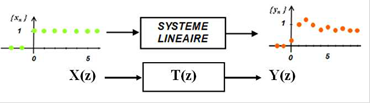
$X(z)$ et $Y(z)$ sont les transformées en $Z$ des signaux causaux $x_n$ et $y_n$.
$T(z)$ est la transmittance du régulateur numérique. Le but est d'étudier la réponse indicielle (c'est-à-dire lorsque $x_n=e(n)$) de ce type régulateur, c'est à dire : quel sera le signal $y_n$ en sortie ?

En physique, la transformée en $Z$ est nommée $X(z)$, en mathématiques le plus souvent $(Zx)(z)$.
Dans ce chapitre, nous utiliserons les deux notations suivant les exercices, en privilégiant celle de physique afin de faciliter les liens avec ce que vous avez vu dans cette matière en première année.

Transformée en $Z$ inverse

Soit $x$ est un signal causal discret. Notons $X(z)$ sa transformée en $Z$.
La suite $(x(n))$ est appelée original ou transformée en $Z$ inverse de la fonction $X$.
On note cet original : $(Z^{-1}X)(n)=x(n)$.

Ainsi, $(Zx)(z)=X(z) \iff (Z^{-1}X)(n)=x(n)$.

L'original de $\dfrac{z}{z-3}$ est la suite causale définie par $x(n)=3^n e(n)$, où $e(n)=0$ si $n\lt 0$ et $e(n)=1$ si $n\ge 0$, puisque la transformée en $Z$ de $x(n)=3^n e(n)$ est la fonction $z\mapsto \dfrac{z}{z-3}$.

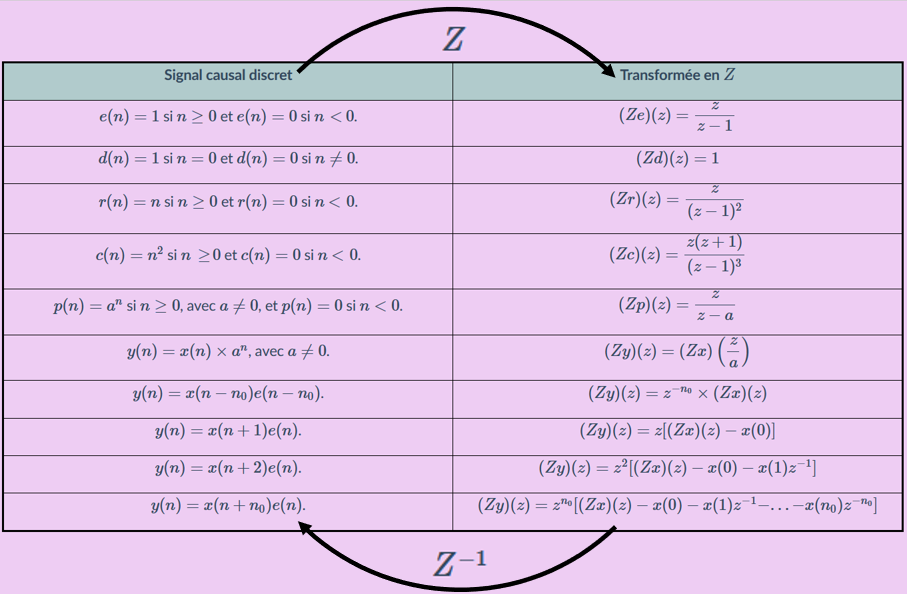
Pour trouver l'original d'une transformée en $Z$ de référence, il suffit d'utiliser la tableau vu au premier chapitre sur la transformée en $Z$, mais en lisant de la droite vers la gauche :

  1. Quel est l'original de la fonction $X(z)=\dfrac{2z}{(z-1)^2}$ ?

  2. Quel est l'original de la fonction $X(z)=1+\dfrac{z(z+1)}{4(z-1)^3}$ ?

Unicité :
Pour une fonction $X:z\mapsto X(z)$ donnée, si l'original $x$ existe alors il est unique.

Linéarité :
Soient $X$ et $Y$ deux transformées en $Z$ ayant des originaux et $\alpha$ et $\beta$ deux nombres réels.
On a : $Z^{-1}(\alpha X +\beta Y)=\alpha Z^{-1}(X) +\beta Z^{-1}(Y)$.

Le but est de trouver l'original de $X(z)=\dfrac{z+1}{z-3}$.

En remarquant que $X(z)=\dfrac{z}{z-3}+\dfrac{1}{z-3}=\dfrac{z}{z-3}+z^{-1}\times \dfrac{z}{z-3}$, déterminer l'original de $X(z)$.

Méthodes de recherche de l'original

Utilisation de la décomposition en éléments simples

L'idée est de couper (on dit décomposer) l'expression de la fonction en morceaux semblables à ceux apparaissant dans le tableau des transformées en $Z$, en particulier comme somme de fractions dont le dénominateur de la forme $(z-a)^n$.

La fonction rationnelle $X(z)=\dfrac{8z-12}{z^2-2z+3} a une forme qui ne correspond à aucune forme du tableau des transformées en $Z$.
Par contre, on peut l'écrire ainsi par décomposition en éléments simples : $X(z)=\dfrac{8z-12}{z^2-2z+3}=\dfrac{6}{z-3}+\dfrac{2}{z-1}$.
On trouve alors deux termes proches de certains éléments du tableau des transformées en $Z$.
Il reste à modifier la forme du numérateur en faisant apparaître le facteur $z$ avec l'astuce $ 1=z\times z^{-1}$.
Ainsi, $\dfrac{8z-12}{z^2-2z+3}=6z^{-1}\times \dfrac{z}{z-3}+2z^{-1}\times \dfrac{z}{z-1}$.
Avec cette forme, l'original peut être trouvé :

Ainsi, l'original de $X(z)=\dfrac{8z}{(z^2-2z-3)}=6z^{-1}\times \dfrac{z}{z-3}+2z^{-1}\times \dfrac{z}{z-1}$ est $x(n)=6 \times 3^{n-1} e(n-1) + 2 e(n-1)$, où $e$ est l'échelon unité discret.

L'instruction partfrac(expression) permet de décomposer en éléments simples l'expression.

Vérifier sur Xcas que la fonction rationnelle $X(z)=\dfrac{8z-12}{z^2-2z+3}$ se décompose en éléments simples sous la forme : $X(z)=\dfrac{8z-12}{z^2-2z+3}=\dfrac{6}{z-3}+\dfrac{2}{z-1}$.

Pour trouver l'original d'une fonction rationnelle en $z$, il suffit de :

Le but est de trouver l'original de la fonction rationnelle définie par $X(z)=\dfrac{2z+3}{(z-1)^2}$.

  1. À l'aide de Xcas, décomposer en éléments simples la fonction rationnelle $X(z)=\dfrac{2z+3}{(z-1)^2}$.

  2. Justifier que $X(z)$ peut s'écrire sous la forme $X(z)=2\times z^{-1}\times \dfrac{z}{z-1} +5\times z^{-1}\times \dfrac{z}{(z-1)^2}$

  3. Déterminer les originaux de $U(z)=\dfrac{z}{z-1}$ et de $V(z)= \dfrac{z}{(z-1)^2}$

  4. En déduire l'original de $X(z)$.

La décomposition directe d'une fonction rationnelle $X(z)$ nécessite souvent l'apparition d'un facteur retard.
Pour avoir une écriture ne faisant pas appel à un tel retard, on peut décomposer non pas directement la fonction rationnelle $X(z)$ mais plutôt le quotient $\dfrac{X(z)}{z}$, comme l'illustre l'exercice suivant :

Le but est de déterminer l'original de la fonction rationnelle définie par $X(z)=\dfrac{2z^3+18z^2-12z}{(z-1)^2(z+3)}$.

  1. Décomposer en éléments simples le quotient $\dfrac{X(z)}{z}$.

  2. En déduire que $X(z)=2\dfrac{z}{(z-1)^2}+5\dfrac{z}{z-1}-3\dfrac{z}{z+3}$.

  3. Déterminer l'original de $X(z)$.

Utilisation de Xcas

Rappel :
Pour déterminer la transformée en $Z$ du signal discret causal $x(n)=(n^2-1)e(n)$, on saisit sur Xcas : ztrans(n^2-1,n,z) (éventuellement factoriser(ztrans(n^2-1,n,z)) pour factoriser l’expression).

Pour obtenir l'original d'une fonction X (d'inconnue z), il suffit de saisir sur Xcas invztrans(X(z),z,n)

On peut retrouver l'original trouvé à la main à l'exercice sur la décomposition de la fonction $X(z)=\dfrac{2z+3}{(z-1)^2}$ avec :

Comme Heaviside correspond à l'échelon unité discret, l'origianl de $X(z)$ est bien défini par $x(n)=(5n-3)e(n-1)$, où $e(n)=1$ si $n\ge 0$ et $e(n)=0$ si $n \lt 0$.

Attention à l'ordre des arguments dans ztrans et invztrans :


Retrouver grâce à Xcas l'original de la fonction définie par $X(z)=\dfrac{2z^3+18z^2-12z}{(z-3)(z-1)^2}$ et comparer avec le résultat obtenu lors de cet exercice, où l'original fut trouvé à la main.

Utilisation de la transformée en $Z$ pour résoudre des équations récurrentes

La démarche générale à suivre comporte trois étapes :

On s'intéresse à un filtre numérique récursif régi par l'équation récurrente suivante : $y(n)-1.5y(n-1)+0.5y(n-2)=e(n)$, où $y$ désigne un signal causal et $e$ l'échelon unité discret.

Xcas ne peut aider qu'à l'étape 3. Chercher les exercices suivant est fondamental pour savoir mettre en oeuvre les deux premières étapes de la méthode.

Soient $x(n)$ et $y(n)$ les termes généraux respectifs de deux signaux discrets causaux représentant, respectivement, l'entrée et la sortie d'un filtre numérique.
Ce filtre est conçu de telle sorte que, pour tout nombre entier $n$ positif ou nul, on a : $y(n)-y(n-1)=\dfrac{1}{2}(x(n)-x(n-2))$.
Notons $Y(z)$ la transformée en $Z$ de $y(n)$ et $X(z)$ la transformée en $Z$ de $x(n)$.

  1. Déterminer la transformée en $Z$ de chaque terme présent dans $y(n)-y(n-1)=\dfrac{1}{2}(x(n)-x(n-2))$.

  2. En déduire que $X(z)$ et $Y(z)$ sont liés par la relation $Y(z)=\dfrac{1}{2}\times \dfrac{1-z^{-2}}{1-z^{-1}} \times X(z)$.

    3. Désormais on suppose que l'entrée est l'échelon unité discret : $x(n)=1$ si $n\ge 0$ et $x(n)=0$ si $n\lt 0$.

  3. Déterminer l'expression de l'original $y(n)$ en fonction de $n$.

  4. En déduire la valeur de $y(0)$.

  5. En déduire la valeur de $y(n)$ lorsque $n>0$.

  6. Représenter graphiquement les termes du signal causal $y$ lorsque le nombre entier $n$ est compris entre -3 et 6.

Pour résoudre des équations aux différences où apparaissent des avances, la même méthode est à appliquer.

Soient $x(n)$ et $y(n)$ les termes généraux respectifs de deux signaux discrets causaux représentant, respectivement, l’entrée et la sortie d’un filtre numérique.
Ce filtre est conçu de telle sorte que, pour tout nombre entier $n$ positif ou nul, on a : $y(n+2)+4y(n+1)+3y(n)=2x(n+1)+x(n)$ avec les conditions initiales $x(0)=0$ et $x(1)=1$.
On suppose dans cet exercice que l'entrée est une rampe causale discrète, c'est-à-dire que $x(n)=0$ si $n\lt 0$ et $x(n)=n$ si $n\ge 0$. Notons $Y(z)$ la transformée en $Z$ de $y(n)$.

  1. Déterminer $y(0)$ et $y(1)$ en utilisant la relation $y(n+2)+4y(n+1)+3y(n)=2x(n+1)+x(n)$.

  2. Déterminer $y(2)$ et $y(3)$ en utilisant la relation $y(n+2)+4y(n+1)+3y(n)=2x(n+1)+x(n)$.

  3. Démontrer que la transformée en $Z$ de $y$ vérifie : $(z^2+4z+3)\times Y(z)=\dfrac{2z^2+z}{(z-1)^2}$.

  4. Décomposer en éléments simples l'expression $\dfrac{Y(z)}{z}$.

  5. Déterminer l'expression de l'original $y(n)$ en fonction de $n$, valable pour tout entier naturel $n$.

Exercices

Lecture du tableau

Déterminer à la main l'original $x$ de chaque fonction $z\mapsto (Zx)(z)$ suivante :

  1. $(Zx)(z)= \dfrac{4z}{z-1}$.

  2. $(Zx)(z)= \dfrac{5z}{(z-1)^2}$.

  3. $(Zx)(z)= \dfrac{3z}{z+1}$.

  4. $(Zx)(z)= \dfrac{z}{3z+1}$.

    Mettre 3 en facteur pour faire apparaître une forme du tableau.

  5. $(Zx)(z)= \dfrac{6}{z-2}$.

  6. $(Zx)(z)= \dfrac{6z}{4z+5}$.

  7. $(Zx)(z)= \dfrac{2z(z+1)}{(z-1)^3}$.

Décomposition

On considère la fonction définie par $X(z)=\dfrac{1}{(z-2)(z-3)}$.

  1. Déterminer les réels $A$ et $B$ tels que $X(z)=z^{-1}\times\dfrac{A z}{z-2}+z^{-1}\times\dfrac{B z}{z-3}$.

  2. En déduire l'original de $X(z)$.

On considère la fonction définie par $X(z)=\dfrac{5z}{(z-2)(z-4)}$.

  1. Déterminer deux constantes $a$ et $b$ telles que, pour tout complexe $z$ tel que $|z|> 4$, $X(z)=\dfrac{a}{z-2}+\dfrac{b}{z-4}$.

  2. En déduire, à la main, l'original de $X(z)$.

  3. Vérifier l'original obtenu sur Xcas.

Soit $X(z)= \dfrac{z^3-3z}{(z+3)(z-1)^2}$. Le but est de déterminer l'original de $X(z)$.

  1. Décomposer en éléments simples le quotient $\dfrac{X(z)}{z}$.

  2. En déduire à la main une décomposition de $X(z)$.

  3. Déterminer les originaux de $z\mapsto \dfrac{z}{z-1}$, $z\mapsto \dfrac{z}{(z-1)^2}$ et de $z\mapsto \dfrac{z}{z+3}$.

  4. En déduire à la main une expression de l'original $x(n)$ en fonction de $n$, avec $n$ entier naturel.

  5. Vérifier sur Xcas l'original obtenu.

Déterminer sur Xcas ou à la main les originaux des transformées en $Z$ suivantes (Xcas peut être utilisé pour décomposer chaque fraction en éléments simples ) :

  1. $(Zx)(z)=\dfrac{z-4}{z-5}$.

  2. $(Zx)(z)=\dfrac{z}{(z-1)(z-2)}$.

  3. $(Zx)(z)=\dfrac{z}{z^2-z-2}$.

  4. $(Zx)(z)=\dfrac{z^2}{(z-1)^2(z+2)}$.

Résolution d'équation aux différences

On considère l'équation récurrente d'ordre 2 : $y(n)-2y(n-1)+y(n-2)=e(n)$ où $y$ est un signal causal discret et $e$ le signal échelon unité discret.

  1. Déterminer les valeurs de $y(-2)$ et de $y(-1)$.

  2. En écrivant l'équation récurrente lorsque $n=0$, déterminer la valeur de $y(0)$.

  3. Déterminer la valeur de $y(1)$.

  4. On note $Y(z)$ la transformée en $Z$ du signal causal $y$.
    En appliquant la transformée en $Z$ aux deux membres de l'équation récurrente, montrer que $Y(z)=\dfrac{z^3}{(z-1)^3}$.

  5. Déterminer l'original $y(n)$ de $Y(z)$.

Soit l’équation de récurrence $y(n)+y(n-1)=e(n)$ où $y$ est un signal causal discret et $e$ la suite échelon unité.

  1. Déterminer l'expression de $y(-1)$.

  2. Déterminer l'expression de $y(0)$.

  3. On note $Y(z)$ la transformée en $Z$ de la suite causale $y(n)$.
    Déterminer l'expression de $Y(z)$.

  4. Déterminer l'expression de l'original $y(n)$ en fonction de $n$, où $n$ est un entier naturel.

Soient $x(n)$ et $y(n)$ les termes généraux respectifs de deux signaux discrets causaux représentant, respectivement, l’entrée et la sortie d’un filtre numérique.
Ce filtre est conçu de telle sorte que, pour tout nombre entier $n$ positif ou nul, on a : $y(n)-y(n-2)=0.04x(n-1)$.

  1. On note $Zx$ et $Zy$ les transformées respectives des signaux causaux $x$ et $y$. Montrer que, pour tout nombre complexe $z$ différent de -1 et 1, on a : $(Zy)(z)=\dfrac{0.04z}{(z-1)(z+1)}(Zx)(z)$.

  2. On suppose désormais que le signal d'entrée est l’échelon unité discret : $x(n)=e(n)$ avec $e(n)=0$ si $n\lt 0$ et $e(n)=1$ si $n\ge 0$.

    1. Montrer que, pour tout nombre complexe $z$ différent de -1 et 1, on a : $(Zy)(z)=\dfrac{0.04z^2}{(z-1)^2(z+1)}$.

    2. Décomposer en éléments simples l'expression $\dfrac{0.04z^2}{(z-1)^2(z+1)}$.

    3. En déduire l'expression de l'original $y(n)$ pour tout entier naturel $n$.

    4. Déterminer $y(2k)$ puis $y(2k+1)$ pour tout nombre entier naturel $k$.

    5. Déterminer $y(2k+1)$ puis $y(2k+2)$ pour tout nombre entier naturel $k$.

    6. Représenter graphiquement les termes du signal causal $y$ lorsque le nombre entier $n$ est compris entre -3 et 6.

Soient $x(n)$ et $y(n)$ les termes généraux respectifs de deux signaux discrets causaux représentant, respectivement, l’entrée et la sortie d’un filtre numérique.
Ce filtre est conçu de telle sorte que, pour tout nombre entier $n$ positif ou nul, on a : $y(n+1)+3y(n)=x(n+1)+x(n)$, avec la condiiton $x(0)=1$ et où l'entrée est la rampe causale discrète : $x(n)=$ si $n\ge 0$ et $x(n)=0$ si $n\lt 0$.

  1. Déterminer les valeurs de $x(1)$ et de $x(2)$.

  2. Démontrer que la transformée en $Z$ de $x$, notée $X(z)$, vérifie : $X(z)= \dfrac{z^3-z^2+2z}{(z-1)^2(z+3)}$.

  3. En déduire l'expression de $x(n)$ en fonction de $n$, valable pour tout $n$ de $\mathbb{N}$.

Exercices en lien avec la physique

Partie analogique

On note $\mathcal{U}$ la fonction échelon unité définie, sur l’ensemble des nombres réels, par : $\mathcal{U}(t)=0$ si $t\lt 0$ et $\mathcal{U}(t)=1$ si $t\ge 0$.
Une fonction définie sur l’ensemble des nombres réels est dite causale lorsque cette fonction est nulle sur l’intervalle $]-\infty;0[$.

On considère un système entée-sortie analogique du premier ordre dont la fonction de transfert $H$ est définie par $H(p)= \dfrac{2}{1+0.5p}$.
On admet que la fonction sortie $s$ modélisant la réponse du système analogique à une entrée correspondant à l’échelon unité $\mathcal{U}$ suit l'équation différentielle suivante : $y'=4-2y$ avec $y(0)=0$.

  1. Déterminer l'expression de $s(t)$ pour tout nombre réel $t$ positif ou nul.

  2. Copier le tableau en fin d'exerice et compléter la ligne donnant les valeurs de $s(t)$ en donnant les valeurs approchées à $10^{-3}$.

Partie numérique

On considère maintenant un système entrée-sortie numérique dont la fonction de transfert $F$ est définie par $\displaystyle F(z)=H\left(100\times \dfrac{1-z^{-1}}{1+z^{-1}}\right)$. Ce système numérique permet d’approcher le système analogique.

L’entrée et la sortie du système numérique sont modélisés, respectivement, par deux suites causales $x$ et $y$. Ces deux suites admettent des transformées en $Z$ notées, respectivement, $X(z)$ et $Y(z)$ telles que $Y(z)=F(z)\times X(z)$.

    1. Montrer que $F(z)= \dfrac{2(1+z^{-1})}{51-49z^{-1}}$.

    2. En déduire que : $51Y(z)-49z^{-1}Y(z)=2X(z)+2z^{-1}X(z)$.

    3. En déduire que, pour tout nombre entier naturel $n$, on a : $y(n)= \dfrac{49}{51} y(n-1)+ \dfrac{2}{51} x(n)+ \dfrac{2}{51} x(n-1)$.

  2. On suppose dans cette question que, pour tout nombre entier $n$, on a : $x(n)=d(n)$, où $d$ est la suite impulsion unité définie par $d(0)=1$ et $d(n)=0$ si $n\neq 0$.

    Grâce à la formule obtenue ci-dessus au 3.b., recopier et compléter le tableau ci-dessous (arrondir à $10^{-3}$ près) :

    $n$ -1 0 1 2 3
    $x(n)=d(n)$ ... ... ... ... ...
    $y(n)$ ... ... ... ... ...

  3. Dans cette question, on suppose que, pour tout entier $n$, on a $x(n)=e(n)$ où $e$ est la suite échelon unité.

    1. Déterminer $X(z)$ la transformée en $Z$ de la suite échelon unité.

    2. On a déjà montré que $Y(z)$ vérifie $51Y(z)-49z^{-1}Y(z)=2X(z)+2z^{-1}X(z)$.
      À l'aide de Xcas, déterminer les réels $a$ et $b$ tels que $Y(z)=a\times \dfrac{z}{z-1} +b\times \dfrac{z}{z-\dfrac{49}{51}}$.

    3. En déduire $y(n)$ pour tout nombre entier naturel $n$.

    4. Compléter la ligne donnant les valeurs de $y(n)$ dans le tableau ci-dessous (arrondir à $10^{-3}$ près) pour comparer les réponses à l’échelon unité du système analogique et du système numérique.

      $n$ 0 10 20 30 40 50 100 150
      $y(n)$ 0.039 ... 1.119 1.140 ... 1.735 ... ...
      $t=0.02n$ 0 0.2 0.4 0.6 0.8 1 2 3
      $s(t)$ 0 0.659 ... ... 1.596 ... 1.963 ...

On considère un système analogique « entrée-sortie » dans lequel le signal d’entrée est représenté par une fonction $e$ et celui de sortie par une fonction $s$.
Une fonction définie sur $\mathbb{R}$ est dite causale si elle est nulle sur l’intervalle $]-\infty;0[$.
On rappelle que la fonction échelon unité $U$ est définie sur $\mathbb{R}$ par : $U(t)=0$ si $t\lt 0$ et $U(t)=1$ si $t\ge 0$. La fonction de transfert $H$ du système est définie par $H(p)=\dfrac{1}{1+2p}$.

Partie A : Étude du système analogique

On suppose, dans le cadre de cette étude, que le signal d'entrée est causal et est donné par $e(t)=U(t)$. On admet que dans ce cadre, $s$ est la solution de l'équation différentielle $2y'+y=1$ avec $y(0)=0$.

  1. Déterminer l'expression de $s(t)$.

Partie B : Étude du système numérisé

On se propose d’approcher la fonction de transfert analogique $H$ par la fonction de transfert numérique $F$ telle que $\displaystyle F(z)=H\left(10\times \dfrac{1-z^{-1}}{1+z^{-1}}\right)$ $\displaystyle =H\left(\dfrac{10z-z}{z+1}\right)$.
L’entrée et la sortie du système numérique sont modélisés respectivement par deux signaux causaux discrets $x$ et $y$, admettant des transformées en $Z$ notées respectivement $X$ et $Y$.

On se place toujours dans le cas où le signal d’entrée du système analogique est $U(t)$.

Le signal d’entrée du système analogique est échantillonné au pas de 0.2.
Ainsi, le signal d’entrée $x$ du système numérique est défini par $x(n)=U(0.2n)$ pour tout nombre entier naturel $n$. Les transformées en $Z$ des signaux $x$ et $y$ vérifient $Y(z)=F(z)\times X(z)$.

  1. Montrer que $F(z)= \dfrac{z+1}{21z-19}$.

  2. Déterminer $X(z)$.

  3. Déterminer $Y(z)$.

  4. En déduire l’expression $y(n)$, pour tout nombre entier naturel $n$.

Partie C : Comparaison des systèmes analogiques et numériques

  1. Compléter le tableau en donnant des valeurs approchées à $10^{-3}$ près des résultats demandés.

    $n$ $y(n)$ $t=0.2n$ $s(t)$
    $0$ ... $0$ ...
    $1$ ... $0.2$ ...
    $5$ ... $1$ ...
    $10$ ... $2$ ...
    $15$ ... $3$ ...
    $20$ ... $4$ ...
    $25$ ... $5$ ...
    $50$ ... $10$ ...

  2. Vérifier que les signaux de sortie analogique et numérique convergent vers la même limite.

  3. Le temps de réponse du système correspond au temps nécessaire pour dépasser 95% de la valeur de la limite.
    Comparer les temps de réponse du système analogique et du système numérique.

Dans un véhicule comportant un dispositif de régulation de la vitesse, le volet d’admission d’air du moteur thermique est contrôlé par le calculateur du véhicule.
Les différentes informations issues des capteurs de position du volet d’admission d’air sont échantillonnées et numérisées par un convertisseur analogique-numérique (CAN) avant d’être traitées par un correcteur numérique.

Dans cet exercice, on étudie la stabilité et la rapidité du correcteur numérique. On note :

  1. Calculer, en hertz, la fréquence d’échantillonnage.

  2. Dans cette question, le signal causal $e(n)$ est l’impulsion unité. Il est donc défini par : $e(0)=1$ et $e(n)=0$ pour tout entier naturel $n$ non nul.

    1. Vérifier que : $S(z)=2.2-\dfrac{z}{z-0.5}$.

    2. En déduire, pour tout entier naturel $n$, l’expression de $s(n)$.
      Préciser la valeur de $s(0)$ et celle de $s(n)$ pour $n$ non nul.

    3. Le système est dit stable si $\displaystyle \lim_{n\to +\infty}s(n)=0$.
      Ce système est-il stable ? Justifier.

  3. Dans cette question, le signal causal $e(n)$ est quelconque.

    1. Montrer que : $\left(1-0.5z^{-1}\right)S(z)=\left(1.2-1.1z^{-1}\right)E(z)$.

    2. En déduire que la relation de récurrence du correcteur est : $s(n)=1.2e(n)-1.1e(n-1)+0.5s(n-1)$.

  4. Dans cette question, le signal causal $e(n)$ est le signal échelon unité : $e(n)=0$ si $n\lt 0$ et $e(n)=1$ sinon.
    On prendra $s(0)=0$.

    1. Exprimer $s(n)$ en fonction de $s(n-1)$ pour $n\ge 1$.

    2. Quelle formule peut-on entrer dans la cellule C2 du tableur pour obtenir, en la recopiant vers la droite, les valeurs successives de $s(n)$ ?

    3. Reproduire sur un tableur et compléter le tableau ci-dessous. On pourra arrondir au millième les valeurs demandées.

    4. À l’aide de ce tableau, conjecturer le sens de variation de $s(n)$ et la valeur de sa limite $L$ quand $n$ tend vers $+\infty$.

    5. Le correcteur est dit rapide si le temps nécessaire pour atteindre 99% de la valeur limite de $s(n)$ est inférieur à 100 ms.
      Le correcteur est-il rapide ? Expliquer.

On se propose d’étudier un système "entrée-sortie" schématisé ci-dessous :

Les signaux d’entrée et de sortie sont liés par l’´equation différentielle $5s'+s=e$. Dans l’exercice, le signal d’entrée $e$ est constant égal à 1 sur $[0;+\infty[$ et le signal de sortie vérifie $s(0)=2$.

Partie A :

  1. Montrer que s$ $vérifie l’´equation différentielle (E) : $5y'+y=1$.

  2. Résoudre l’équation homogène (H) : $5y'+y=0$.

  3. Déterminer une solution particulière constante de (E).

  4. Montrer que $s(t)=e^{-0.2t}+1$.

Partie B :

On échantillonne le système avec un pas de 0.5. On note donc $x(n)=s(0.5n)$ et on admet que l’on peut remplacer $s'(0.5n)$ par $\dfrac{x(n+1)-x(n)}{0.5}$ dans l’équation différentielle.

  1. Montrer que l’´equation devient (E') : $x(n+1)=0.9x(n)+0.1$ avec $x(0)=2$.

  2. Déterminer une expression de $(Zx)$, la transformée en $Z$ de $x$.

  3. Décomposer $\dfrac{(Zx)(z)}{z}$ en éléments simples.

  4. En déduire une expression de $x$.

Partie C :

  1. Comparez les résultats obtenus aux parties A et B après avoir complété le tableau ci-dessous :

On désigne par $e_n$ et $s_n$ respectivement les valeurs de l’entrée et de la sortie du filtre ci-dessous à l’instant $nT_e$.

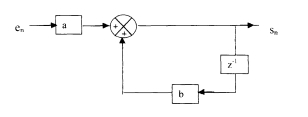
On admet que l’algorithme de ce filtre peut s’écrire : $s_n=a\times e_n+b\times s_{n-1}$ ($a$ et $b$ sont deux coefficients constants).

  1. Montrer que $\dfrac{S(z)}{E(z)} = a\dfrac{z}{z-b}$. ($S(z)$ et $E(z)$ sont les transformées en $Z$ respectives de $(s_n)$ et de $(e_n)$.

  2. Déterminer la réponse indicielle $s_n$, à l'instant $nT_e$, lorsque $a= \dfrac{1}{4}$ et $b=\frac{9}{10}$, c'est-à-dire lorsque l'entrée est le signal causal correspondant à l'échelon unité discret.

Soit $(u_n)$ la suite définie par la formule de récurrence suivante : pour tout entier naturel $n$ : $6u(n+1)=u(n)+u(n-1)$, avec $u(0)=0$ et $u(1)=1$.
On note $U(z)$ la transformée en $Z$ de la suite causale $(u(n))$.

  1. Démontrer que $U(z)= \dfrac{6z}{6z^2-z-2}$.

  2. Déterminer les réels $a$ et $b$ tels que $U(z)=a \dfrac{z}{z+\dfrac{1}{2}} +b \dfrac{z}{z- \dfrac{2}{3}}$.

  3. Déterminer l'expression de $u(n)$ en fonction de $n$.

Soit $(u_n)$ la suite définie par la formule de récurrence suivante : pour tout entier naturel $n$ : $u(n+1)=2u(n)-u(n-1)+e(n)$, avec $u(0)=0$ et $u(1)=1$.
Déterminer l'expression de $u(n)$ en fonction de $n$.

En notant $U(z)$ la transformée en $Z$ de la suite causale $(u(n))$, montrer d'abord que $U(z)= \dfrac{z^2}{z^3-3z^2+3z-1}$.

On considère un filtre analogique de type passe bas du premier ordre utilisé dans de nombreux modules électroniques. Il est constitué d’un résistor ayant une résistance $R$ et d’un condensateur de capacité $C$.
Les tensions d’entrée et de sortie, exprimées en volt, dépendent du temps $t$ exprimé en seconde.
On les modélise par des fonctions $e$ et $s$ définies sur l’intervalle $[0;+\infty[$ et qui vérifient : $s(0)=0$ et $RCs'(t)+s(t)=e(t)$ pour tout $t\ge 0$.
On étudie dans l’exercice le cas particulier où $RC=10^{-2}$ seconde et $e(t)=1$ pour tout $t\ge 0$. La fonction $s$ est donc la fonction nulle en $0$ vérifiant sur $[0;+\infty[$ l’équation différentielle : $0.01y'(t)+y(t)=1$ (E), d’inconnue la fonction $y$, dérivable sur $[0;+\infty[$ et de fonction dérivée $y'$.

Partie A : cas analogique

  1. Déterminer la fonction solution $s$ l'équation différentielle (E) en prenant en compte la condition initiale $s(0)=0$.

  2. Déterminer la tension de sortie à très long terme.

  3. Étudier les variations de la fonction $s$ sur l’intervalle $[0;+\infty[$.

  4. On appelle temps de réponse du filtre analogique, le temps nécessaire pour que la tension de sortie atteigne 95% de celle à très long terme.
    Déterminer le temps de réponse de ce filtre analogique.

Partie B : cas discrétisé

On s’intéresse dans cette partie à un système d’entrée-sortie numérique destiné à approcher le système analogique étudié dans l’exercice.
La tension d’entrée $e(t)$, exprimée en volt, est échantillonnée à la cadence $T_e$ avec $T_e=10^{-3}$ seconde.
On obtient ainsi un signal discret causal an vérifiant pour tout entier $n\ge 0$ : $a_n=e(nT_e)=1$. Par échantillonnage à la cadence $T_e$ de la fonction $s$ et discrétisation de l’équation $RCs'(t)+s(t)=e(t)$, on définit un signal discret causal $b_n$ vérifiant, pour tout $n\ge 1$ : $RC \dfrac{b_n-b_{n-1}}{T_e} +b_n=a_n$.

  1. Montrer que pour tout entier $n\ge 1$ : $b_n= \dfrac{1}{11} a_n+ \dfrac{10}{11} b_{n-1}$.

  2. Désormais, on suppose que pour tout entier $b_n= \dfrac{1}{11} a_n+ \dfrac{10}{11} b_{n-1}$.
    Reproduire et compléter le tableau ci-contre en donnant les valeurs de $a_n$, $b_{n-1}$ et $b_n$ arrondies à $10^{-3}$ près pour $n$ compris entre 0 et 3.

    $n$ $0$ $1$ $2$ $3$
    $a_n$ ... ... ... ...
    $b_{n-1}$ ... ... ... ...
    $b_n$ ... ... ... ...

    1. On rappelle que le signal causal an vérifie : $a_n=1$ pour tout entier $n\ge 0$. Donner la transformée en $Z$, notée $A(z)$, du signal $a_n$.

    2. Montrer que $B(z)= \dfrac{z}{z-1} - \dfrac{10}{11} \times \dfrac{z}{z-\dfrac{10}{11}}$.

    3. En déduire l'expression de $b_n$ en fonction de $n$.

    1. Déterminer la limite de $b_n$ et le temps de réponse de ce filtre numérique.

    2. Comparer les limites et les temps de réponse des deux filtres.

  5. On estime que l’équivalent numérique du filtre analogique est satisfaisant lorsque l’écart relatif entre $b_n$ et $s(nT_e)$, pour $n\ge 1$, est strictement inférieur à 1%, c’est-à-dire lorsque : $\left|\dfrac{b_n}{s(nT_e)} -1\right|\lt 0.01$.
    Déterminer la plus petite valeur de $n$ pour laquelle l'écart relatif entre $b_n$ et $s(nT_e)$ est strictement inférieur à 1%.

Dans une voiture, la pédale d'accélérateur actionne le volet d'admission d'air du moteur thermique. Lors de la mise en fonctionnement du régulateur, celui-ci actionne directement ce volet d'air pour maintenir la vitesse du véhicule constante.

Dans les véhicules assez récents, un calculateur numérique gère l'ensemble des informations provenant de divers capteurs qui donne des ordres aux actionneurs du volet et assure aussi leur asservissement.

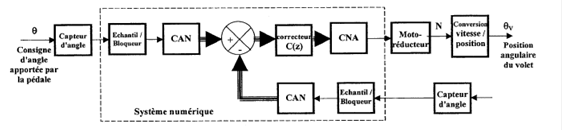
On note $(x(n))$ la suite causale des valeurs à l'entrée du correcteur numérique tandis que la sortie délivre la suite causale $(y(n))$.
On admet que $y(0)=0$.
On admet que ces suites sont liées par la relation de récurrence suivante définie pour tout entier naturel $n$ : $y(n)=1.5x(n)-x(n-1)+0.8y(n-1)$. (E)
On note $Y(z)$ la transformée en $Z$ de $(y(n))$ et $X(z)$ celle de la suite causale $(x(n))$.
On admet qu'il y a une mesure toutes les 0.1 seconde.

  1. Dans cette question, le signal d'entrée est défini par $x(n)=e(n)$, le signal échelon unité causal.

    1. Simplifier l'équation (E) pour exprimer $y(n)$ en fonction de $y(n-1)$ pour $n\ge 1$.

    2. Calculer la valeur de $y(1)$ et de $y(2)$.

    3. Quelle formule peut-on entrer dans la cellule C2 du tableur pour obtenir, en la recopiant vers la droite, les valeurs successives de $y(n)$ ?

    4. Reproduire et compléter le tableau ci-dessous. On arrondira au millième les valeurs demandées.

  2. Dans cette question uniquement le signal d'entrée est quelconque.

    Justifier que $Y(z)= \dfrac{1.5-z^{-1}}{1-0.8z^{-1}} \times X(z)$.

Dans toutes les questions suivantes, le signal causal $x(n)$ est le signal échelon unité : $e(n)=0$ si $\lt 0$ et $e(n)=1$ sinon.

  1. Déterminer la réponse indicielle de ce correcteur, c'est à dire donnée l'expression de $y(n)$ lorsque $(x(n))$ est le signal échelon unité discret causal.

  2. Déterminer la limite $L$ du signal de sortie $(y(n))$. Y-a-t-il stabilité du correcteur ?

  3. Déterminer le temps de réponse, c'est à dire le temps nécessaire pour que l'écart entre le signal de sortie et sa valeur limite soit inférieur à 5%.

Demander le programme !


Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲