Les algorithmes gloutons dans la section Algorithmique.
-
Contenus : Algorithmes gloutons
-
Capacités attendus : Résoudre un problème grâce à un algorithme glouton.
-
Commentaires : Exemples : problèmes du sac à dos ou du rendu de monnaie. Les algorithmes gloutons constituent une méthode algorithmique parmi d’autres qui seront vues en terminale.
Introduction à l'algorithme glouton
Dans ce chapitre nous allons aborder la notion d'optimisation d'un problème.
Un problème d'optimisation est un problème pour lequel on cherche la meilleure solution (selon un critère défini) dans un ensemble de solutions possibles.
Quelques exemples de problèmes d'optimisation :
-
Rendre la monnaie avec un minimum de pièces.
-
Ranger le maximum d'éléments : sac à dos, colis dans un camion, etc.
-
Réservation de véhicules dans une société pour minimiser la taille du parc nécessaire.
-
Parcourir un ensemble de lieux en minimisant le temps ou la distance nécessaire.
-
Et d'autres.
On parle de solution optimale toute une solution qui fait partie des solutions possibles et qui est la meilleure des solutions selon le critère défini.
-
Pour un rendu de monnaie, le critère pour la solution optimale sera le nombre de pièces et/ou billets.
-
Pour un parcours de lieux, le critère peut être le nombre de lieux ou la distance parcourue (minimale, maximale).
-
Pour un système de réservation, le critère peut être le nombre de réservations ou la durée de réservation.
-
Etc.
Les algorithmes gloutons sont souvent utilisés pour résoudre ces problèmes d'optimisation . On cherche une solution optimale en effectuant le meilleur choix possible à chaque étape de l'algorithme. Dans ce type de résolution, il n'y a pas de retour en arrière. Lorsqu'un choix est fait, il n'est pas modifié par la suite. On se retrouve donc à chaque étape, avec un problème de plus en plus petit à résoudre.
Attention toutefois, cette méthode ne fournit pas systématiquement la solution optimale au problème proposé.
Exemple classique : le rendu de monnaie.
Nous allons étudier un problème d'optimisation classique : le problème du rendu de monnaie de manière optimale. On cherche à rendre la monnaie avec un nombre minimal de pièces et billets.
-
Pièces : 0,01 ; 0,02 ; 0,05 ; 0,1 ; 0,2 ; 1 ; 2 .
-
Billets : 5 ; 10 ; 20 ; 50 ; 100 ; 200; 500.
Voici notre système de monnaie (exprimé en euros) :
On cherche par exemple à rendre $53$ euros. On peut dans un tableau énumérer quelques solutions possibles et choisir celle qui minimise le nombre de pièces et de billets.
| Rendus de monnaie | Nombre de pièces et de billets |
|---|---|
| $5300 \times 0,01 €$ | 5 300 |
| $53 \times 1 €$ | 53 |
| $5 \times 10 + 1 \times 2 + 1 \times 1 €$ | 7 |
| $ 2 \times 20 + 3 \times 5 + 1 \times 2 € $ | 6 |
| $ 1 \times 50 + 1 \times 1 + 1 \times 2 € $ | 3 |
L'utilisation de ce type de méthode est très coûteux en temps de calcul car il faut explorer toutes les possibilités avant de trouver la solution optimale.
Présentation en vidéo.
L'algorithme glouton
Un algorithme glouton est un algorithme dans lequel on procède étape par étape en faisant, à chaque étape,
le meilleur choix possible.
On ne remet jamais en cause les choix faits aux étapes passées.
Dans notre cas nous allons rendre la monnaie en commençant par la pièce ou le billet avec la plus grande valeur possible (en restant inférieur à la somme à rendre). Cela correspond à notre dernière ligne de tableau ($ 1 \times 50 + 1 \times 1 + 1 \times 2 € $). On recommence ainsi jusqu'à obtenir une valeur nulle.
On note :
-
systeme : liste des pièces et des billets
-
somme : montant à obtenir
-
somme_restante : montant qui reste à rendre
-
monnaie : liste qui contient les valeurs rendues
- initialiser monnaie à une liste vide
- initialiser la somme_restante à somme
- tant que somme_restante > 0 :
- On choisit la plus grande valeur dans systeme inférieure à somme_restante
- on ajoute cette valeur à monnaie
- on retire cette valeur à somme_restante
- renvoyer monnaie
Voici ci-dessous une animation JavaScript qui vous permet de visualiser les étapes de l'algorithme ci-dessus de rendu de monnaie :
Sélectionner un temps de pause (en millisecondes) entre chaque étape permettant de déterminer le nombre de pièces à rendre :
Entrez le montant à rendre :
Il reste tout à rendre.
Tableau donnant l'ensemble des pièces à rendre suivant leur valeur :
| Reste | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| système monétaire | 500 | 200 | 100 | 50 | 20 | 10 | 5 | 2 | 1 | 0.50 | 0.20 | 0.10 | 0.05 | 0.02 | 0.01 |
| Nombre de pièces à rendre | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Reprenons notre exemple avec somme=$53$ et systeme=$[0.01, 0.02, 0.05, 0.1, 0.2, 1, 2, 5, 10, 20, 50]$.
Voici la liste des étapes :
| Étapes | liste des monnaies rendues | somme restant à rendre |
|---|---|---|
| Initialisation | monnaie=[] | somme_restante=$53$ |
| Etape 1 | monnaie = $[50]$ | somme_restante=$3$ |
| Etape 2 | monnaie = $[50,2]$ | somme_restante=$1$ |
| Etape 2 | monnaie = $[50,2,1]$ | somme_restante=$0$ |
Notre solution dépend du nombre de pièces et de billets disponibles. Si nous sommes limités sur certaines pièces et/ou certains billets, les résultats seront différents.
-
Traiter à la main comme précédemment le rendu de monnaie dans le cas d'un système S = $[1,2,5,50,100]$ et d'une somme : $ 27 €.$
-
Comment gérer le rendu de monnaie dans le cas d'un système S = $[1,2,5,50,100]$ et d'une somme : $ 27 €$ dans le cas où l'on ne dispose que de quatre pièces de chaque type ?
Quelles sont les préconditions et les postconditions de cet algorithme ?
Solution et solution optimale
On peut se poser la question pourquoi notre système monétaire ne possède pas de pièces ou de billets de 7 € ?
L'exercice suivant va vous permettre de mieux comprendre cela.
On considère le cas dans cet exercice du système S = $[1,2,5,7,10,20]$ et d'une somme : $ 14 €$.
-
Déterminer les pièces et billets rendus dans le cas de l'utilisation de l'algorithme glouton.
-
Quelles pièces ou billets suffit-il de rendre pour rendre 14€ ?
-
L'algorithme glouton donne-t-il toujours une solution optimale ?
Il existe des conditions sur le système pour que l'algorithme glouton soit optimal. Si le sujet vous intéresse, vous pouvez faire des recherches ou consulter cette partie de page Wikipedia.
Dans le système de pièces de la Zone Euro, l'algorithme glouton donne toujours une solution optimale.
Avant la décimalisation définitive de 1971, le système monétaire britannique reposé sur une subdivision de valeurs qui remontait à l'époque carolingienne.
Voici les principales valeurs de cet ancien système, appelé système impérial :
-
1 penny
-
3 pence (pluriel de penny)
-
6 pence (ou demi-shilling)
-
12 pence (appelé shilling)
-
24 pence (appelé florin)
-
30 pence (appelé demi-couronne)
-
60 pence (appelé couronne)
-
240 pence (appelé livre)
(source : wikipedia)
-
Quel sera le rendu de monnaie de 48 pence avec le système imperial $[240, 60, 30, 24, 12, 6, 3, 1]$ dans le cas où on utilise l'algorithme glouton ?
-
Pouvez-vous trouver une solution plus optimale que celle obtenue par l'algorithme glouton ?
On considère désormais le système suivant : $S = [2, 5, 10, 20, 50, 100]$ et la somme à rendre de $21€$.
-
Proposez une trace d'exécution de l'algorithme glouton sur ce système et cette valeur à rendre.
-
Que remarquez-vous ?
-
Pouvez-vous trouver une solution (optimale ?) à ce problème de rendu de monnaie ?
Un algorithme glouton consiste à effectuer des choix "locaux" (dans le cas du rendu de monnaie : rendre la plus grande valeur possible), choix qui ne seront plus jamais remis en cause mais qui permettent de réduire le problème à un problème plus "simple" (dans le cas du rendu de monnaie : rendre la somme diminuée de la valeur maximale)
Les algorithmes gloutons constituent une méthode algorithmique, parmi d'autres, pour résoudre des problèmes, en particulier d'optimisation.
Lorsqu'un algorithme glouton permet d'obtenir une solution, celle-ci n'est pas forcément la solution optimale au problème.
Un algorithme glouton peut ne trouver aucune solution bien que des solutions existent.
Nous verrons en terminale une méthode pour créer un algorithme, pas trop coûteux, qui permet d'obtenir la solution optimale à coup sûr.
Voici une vidéo qui reprend les limites de l'algorithme glouton dans le cas du rendu de monnaie au travers des exercices précédents :
Implémentation de l'algorithme glouton
-
Programmer l'algorithme glouton de rendu de monnaie en langage python.
Pour cela, programmer une fonctionrendu_monnaie_gloutonqui possède comme paramètres-
un système de pièces et de billet
systemesous forme de liste de nombres ; -
une somme à rendre
somme.
Cette fonction renvoie une liste de nombres qui caractérise la monnaie à rendre.
-
penser à trier par ordre décroissant la liste des pièces et billets.
-
Vous pouvez prendre comme jeu de test de l'exemple de présentation.
-
-
Améliorer cette fonction pour prendre en compte le fait que l'algorithme ne trouve pas de solution dans certains cas.
prendre certains exemples du chapitre 1.3 pour tester cette version améliorée.
Des vidéos pour vous aider à comprendre.
Voici un exercice à faire en autonomie pour tester votre maîtrise de
l'algorithme glouton de dichotomie.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Plutôt que de faire des soustractions successives comme vu précédemment,
vous pouvez ici utiliser les opérateurs % et // de
la division euclidienne pour trouver plus rapidement le nombre de pièces
de chaque valeur.
Problème du sac à dos
Pour partir en randonnée, vous disposez d'un sac à dos. Afin de pouvoir marcher longtemps chaque jour, vous décidez de limiter la masse totale transportée
à 17kg. Cette limitation ne vous permet pas de pouvoir transporter tous les éléments que vous aimeriez emporter.
Vous décidez de donner une note "utilité" à chacun des objets.
| Objet | eau | nourriture | nécessaire de cuisine | couverture | matelas | tente | gaz | lampe | console de jeu | change | jumelle | cartes | pull | machette | livre de chevet |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Masse | 3 | 4.3 | 2.2 | 1 | 1.5 | 3.4 | 0.8 | 0.5 | 2.1 | 2.8 | 1.3 | 0.5 | 0.8 | 2.4 | 0.3 |
| Utilité | 20 | 15 | 12 | 6 | 4 | 18 | 13 | 10 | 7 | 11 | 9 | 8 | 8 | 5 | 2 |
Vous cherchez à maximiser l'utilité totale des objets emportés dans votre sac à dos.
Sans ordinateur
-
Le fait de prendre ou non chaque objet est un choix binaire : on peut prendre 3 litres d'eau ou pas, une couverture ou pas, etc.
Si vous voulez tester toutes les possibilités pour remplir votre sac à dos afin de trouver la ou les solutions optimales, combien de cas différents devriez-vous étudier ? -
Si vous utilisez un algorithme glouton avec comme critère l'optimisation de la masse, c'est-à-dire en faisant en sorte de mettre d'abord l'objet le plus lourd, puis le deuxième le plus lourd, etc. sans jamais remettre en cause vos choix précédents, c'est-à-dire sans jamais enlever du sac un objet déjà mis, quelle sera la composition de votre sac à dos si vous limitez la masse totale à 17 kilogrammes ?
-
Si vous utilisez un algorithme glouton avec désormais comme critère l'optimisation de l'utilité, quelle sera la composition de votre sac à dos ? (La masse totale reste encore limitée à 17 kg)
Avec ordinateur
N'étant pas certain.e.s de la pertinence du résultat obtenu, vous décidez de choisir les objets non plus en fonction de leur seule
utilité mais en fonction de leur utilité massique c'est-à-dire en fonction du rapport $\dfrac{utilité}{masse}$.
Par exemple, l'utilité massique de l'eau est de $\dfrac{20}{3}\approx 6.666666666666667$.
De plus, plutôt que de tout recalculer à la main, vous préférez utiliser une programme informatique en langage Python.
L'ensemble des objets pouvant être choisis pour la randonnée est implémentée par une liste de dictionnaires, chaque dictionnaire représente
un objet et a trois clés :
"Nom" associé au nom de l'objet, "Masse" associée à la masse de l'objet et Utilite associée à son utilité.
Par exemple, le dictionnaire associé à l'objet eau doit devenir
{'Nom': 'eau', 'Masse': 3, 'Utilite': 20}.
Voici un fichier donnant cette liste.
-
Proposer un script Python qui permet de compléter chaque dictionnaire de la liste en rajoutant une association dont la clé est la chaîne de caractères
En cas de difficultés, en cliquant ici, il est possible d'obtenir un code à trous à compléter."Utilite_massique"et dont la valeur associée est l'utilité massique de l'objet considéré.
Par exemple, le dictionnaire associé à l'objet eau doit devenir{'Nom': 'eau', 'Masse': 3, 'Utilite': 20, 'Utilite_massique': 6.666666666666667}.Copier puis compléter le script suivant en vous servant des commentaires.
liste_objets = [{'Nom': 'eau', 'Masse': 3, 'Utilite': 20}, {'Nom': 'nourriture', 'Masse': 4.3, 'Utilite': 15}, {'Nom': 'cuisine', 'Masse': 2.2, 'Utilite': 12}, {'Nom': 'couverture', 'Masse': 1, 'Utilite': 6}, {'Nom': 'matelas', 'Masse': 1.5, 'Utilite': 4}, {'Nom': 'tente', 'Masse': 3.4, 'Utilite': 18}, {'Nom': 'gaz', 'Masse': 0.8, 'Utilite': 13}, {'Nom': 'lampe', 'Masse': 0.5, 'Utilite': 10}, {'Nom': 'console', 'Masse': 2.1, 'Utilite': 7}, {'Nom': 'change', 'Masse': 2.5, 'Utilite': 11}, {'Nom': 'jumelle', 'Masse': 1.3, 'Utilite': 9}, {'Nom': 'cartes', 'Masse': 0.5, 'Utilite': 8}, {'Nom': 'pull', 'Masse': 0.8, 'Utilite': 8}, {'Nom': 'machette', 'Masse': 2.4, 'Utilite': 5}, {'Nom': 'livre', 'Masse': 0.3, 'Utilite': 2}] # rajout de l'association liée à l'utilité massique : for objet in liste_objets: objet[...] = ... / ... # vérification de l'ajout : print(liste_objets)Attention ! Il y a d'autres manières d'écrire le script demandé, manières tout aussi pertinentes que celle proposée ci-dessus avec des trous.
-
Quel prétraitement sur la liste de dictionnaires est-il pertinent d'effectuer afin de pouvoir écrire un algorithme glouton renvoyant un résultat selon le critère pris en compte ?
-
Pour trier une liste de dictionnaires
En cas de difficultés, en cliquant ici, il est possible d'obtenir un code à trous à compléter.liste_a_trier, du type de ceux de cet exercice, par ordre croissante de la masse, il suffit de saisir :liste_triee = sorted(liste_a_trier, key=lambda dico : dico["Masse"]).
Proposer une implémentation en langue Python de l'algorithme glouton qui à partir de la liste des objets disponibles affiche la liste des objets à prendre en maximisant le critère de l'utilité massique.Copier puis compléter le script suivant en vous servant des commentaires.
liste_objets = [{'Nom': 'eau', 'Masse': 3, 'Utilite': 20}, {'Nom': 'nourriture', 'Masse': 4.3, 'Utilite': 15}, {'Nom': 'cuisine', 'Masse': 2.2, 'Utilite': 12}, {'Nom': 'couverture', 'Masse': 1, 'Utilite': 6}, {'Nom': 'matelas', 'Masse': 1.5, 'Utilite': 4}, {'Nom': 'tente', 'Masse': 3.4, 'Utilite': 18}, {'Nom': 'gaz', 'Masse': 0.8, 'Utilite': 13}, {'Nom': 'lampe', 'Masse': 0.5, 'Utilite': 10}, {'Nom': 'console', 'Masse': 2.1, 'Utilite': 7}, {'Nom': 'change', 'Masse': 2.5, 'Utilite': 11}, {'Nom': 'jumelle', 'Masse': 1.3, 'Utilite': 9}, {'Nom': 'cartes', 'Masse': 0.5, 'Utilite': 8}, {'Nom': 'pull', 'Masse': 0.8, 'Utilite': 8}, {'Nom': 'machette', 'Masse': 2.4, 'Utilite': 5}, {'Nom': 'livre', 'Masse': 0.3, 'Utilite': 2}] # rajout de l'utilité massique for objet in liste_objets: objet[...] = ... / ... print(liste_objets) # tri de la liste en fonction de l'utilité massique décroissante : liste_triee = sorted(..., key=lambda dico : dico[...]) # pour avoir les objets à plus grande utilité massique en premier : liste_triee.... # Vérification du contenu : print(liste_triee) # algorithme glouton : masse_sac = ... a_emporter = ... j = 0 # position de l'objet étudié while ... : if masse_sac + liste_triee[...][...] <= 17: masse_sac = ... a_emporter.append(liste_triee[...][...]) j = ... print(...)Attention ! Il y a d'autres manières d'écrire le script demandé, manières tout aussi pertinentes que celle proposée ci-dessus avec des trous.
-
Qu'allez-vous emmener en randonnée ?
Voici un exercice à faire en autonomie pour tester votre maîtrise du
principe d'algorithme glouton sur un problème déjà étudié différemment :
la conversion binaire d'unnnombre décimal.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Si vous n'arrivez pas à compléter la version sans trous,
cliquer ici pour obtenir un code à trous à copier-coller puis à compléter.
Copier dans la console de codex lié à l'exercice le script suivant sans effacer les tests puis compléter le code :
def binaire(nombre):
if nombre == 0:
return ...
resultat = ""
puissance_max = 1
while 2 * puissance_max <= nombre :
puissance_max = ...
# puissance_max contient désormais la plus grange puissance de 2 inférieure à nombre
# par exemple 32 (=2^5) pour le nombre 43
while puissance_max > ...:
if ...:
resultat = resultat + "1"
nombre = ...
else:
resultat = resultat + ...
puissance_max = ...
return resultatAttention ! Il y a d'autres manières d'écrire le script demandé, manières tout aussi pertinentes que celle proposée ci-dessus avec des trous.
Voici un exercice à faire en autonomie pour tester votre maîtrise du
principe d'algorithme glouton sur un problème nouveau.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Si vous n'arrivez pas à compléter la version sans trous,
cliquer ici pour obtenir un code à trous à copier-coller puis à compléter.
Copier dans l'éditeur de codex lié à l'exercice le script suivant sans effacer les tests puis compléter le code :
def partition(liste):
# les deux lignes suivantes reviennent à l'instruction : liste.sort(reverse=True)
liste.sort()
liste.reverse()
# partie à compléter
liste_1 = ...
liste_2 = ...
somme_1 = ...
somme_2 = ...
for elt in liste:
if ...:
liste_1.append(elt)
somme_... = ...
else:
...
...
return liste_1, liste_2Attention ! Il y a d'autres manières d'écrire le script demandé, manières tout aussi pertinentes que celle proposée ci-dessus avec des trous.
QCM
Questions issues de la Banque Nationale de Sujets
Propriétaire des ressources ci-dessous : ministère de l'Éducation nationale et de la jeunesse, licence CC BY SA NC
Voici une sélection de questions issues de la banque nationale de sujets, répondez à ces questions (attention, cette sélection n'est pas exhaustive).
À quelle catégorie appartient l’algorithme classique de rendu de monnaie ?
Réponses :
A- Les algorithmes de classification et d'apprentissage.
B- Les algorithmes de tri.
C- Les algorithmes gloutons.
D- Les algorithmes de mariage stable.
On dispose en quantité illimité de pièces de 1 euro, 2 euros et 5 euros. On veut totaliser une somme de
18 euros.
Quelle est la solution donnée par l’algorithme glouton ?
Réponses :
A- [5, 5, 5, 2, 1].
B- [5, 5, 5, 2, 2, 1].
C- [5, 5, 2, 2, 2, 1, 1].
D- [5, 2, 2, 2, 2, 1, 1, 1, 1, 1].
On dispose de sacs de jetons portant les nombres 10, 5, 3 et 1.
On veut obtenir un total de 21 en utilisant ces jetons.
Si on utilise le principe de l'algorithme glouton, quelle addition va-t-on réaliser pour obtenir ce total de 21 ?
Réponses :
A- 5 + 5 + 5 + 5 + 1.
B- 10 + 5 + 3 + 3.
C- 10 + 5 + 5 + 1.
D- 10 + 10 + 1.
Autres QCM
Les QCM suivants sont des QCM modifiés à partir de QCM se trouvant sur le site https://genumsi.inria.fr.
Parmi les phrases suivantes, laquelle est vraie ?
Réponses :
A- Un algorithme glouton fournit toujours une solution optimale.
B- Un algorithme glouton est généralement moins coûteux en temps que d'autres méthodes d’optimisation.
C- Un algorithme glouton étudie tous les cas possibles pour déterminer la solution optimale.
D- Un algorithme glouton peut revenir en arrière en cas de blocage.
Un sherpa doit traverser la montagne pour vendre des marchandises dans le village voisin. Il ne peut transporter plus de 20kg dans son sac à dos et
il dispose de 6 objets de poids différents et de valeurs différentes.
Voici cette liste d'objets sous forme d'un dictionnaire dont les clés sont le nom de l'objet nom, la valeur en euros valeur,
et la masse en kg masse.
Objets=[{nom:"A", valeur:10, masse:8},{nom:"B", valeur:8, masse:12},
{nom:"C", valeur:5, masse:3},{nom:"D", valeur:9, masse:6},
{nom:"E", valeur:7, masse:5},{nom:"F", valeur:6, masse:2}]
Il se demande quels objets choisir pour transporter la valeur totale maximale dans son sac tout en ne dépassant pas 20 kg.
Quels objets doit-il mettre dans son sac s'il applique un algorithme glouton dans la résolution de ce problème ?
Réponses :
A- Objet "B" puis objet "A"
B- Objet "A" puis objet "D" puis objet "E"
C- Objet "C" puis objet "D" puis objet "E" puis objet "F"
D- Objet "B" puis objet "E" puis objet "C"
Un commerçant vit dans un pays dont le système monétaire est constitué de pièces et de billets ayant pour valeur faciale : 1, 2, 5, 10, 20, 50, 100, 200
et 500. On note euros la liste des valeurs faciales disponibles pour un rendu de monnaie par le commerçant. (le
commerçant peut posséder plusieurs pièces ou billets de même valeur)
euros = [1, 1, 1, 1, 1, 2, 2, 2, 5, 10, 10, 10, 20, 50, 100, 100, 100, 200, 500]
On souhaite écrire un programme qui affiche la monnaie que le commerçant devra rendre.
On note s la somme à rendre en supposant que celle-ci est inférieure ou égale à 1000.
Parmi les 4 programmes suivants, lequel est correct ?
Réponses :
A-
def monnaie(s) :
i = len(euros)
p = 0
while s > 0 :
if s >= euros[i] :
p +=1
s -= euros[i]
else :
i = i - 1
return pB-
def monnaie(s) :
i = len(euros) - 1
p = 0
while s > 0 :
if s >= euros[i] :
p +=1
s -= euros[i]
else :
i = i - 1
return pC-
def monnaie(s) :
i = len(euros) - 1
p = 0
while s >= 0 :
if s >= euros[i] :
p +=1
s -= euros[i]
else :
i = i - 1
return pD-
def monnaie(s) :
i = len(euros) - 1
p = 0
while s > 0 :
if s > euros[i] :
p +=1
s -= euros[i]
else :
i = i - 1
return p
On dispose de sacs de jetons portant les nombres 10, 8, 5 et 1.
On veut obtenir un total de 24 en utilisant ces jetons.
Si on utilise le principe de l'algorithme glouton, quelle addition va-t-on réaliser pour obtenir ce total de 24 ?
Réponses :
A- 8+8+8
B- 10+8+5+1
C- 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
D- 10+10+1+1+1+1
Un système monétaire contient les pièces suivantes : 24, 15, 8, 5 et 2 unités. Le nombre de pièces de chaque sorte n'est pas limité.
On souhaite rendre 40 unités.
Quelle est la solution donnée par l'algorithme glouton de rendu de monnaie ?
Réponses :
A- [15, 15, 5, 5]
B- [24, 8, 8]
C- [15, 15, 8, 2]
D- L'algorithme échouera à rendre la somme de 40 unités.
Voici un arbre, on le parcourt en partant du haut (la racine) et en descendant de branche en branche (les nœuds) jusqu'à arriver à une feuille.
Par exemple on peut faire le parcours Racine 4 puis nœud 5 puis nœud 4 puis feuille 6.
Considérons un algorithme Glouton de parcours (racine vers feuille) de cet arbre, Sélectionnant le nœud le plus grand à chaque étape.
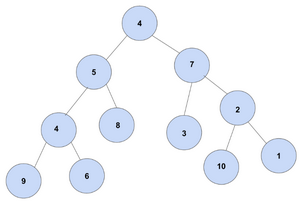
Quel chemin cet algorithme Glouton va-t-il parcourir ?
Réponses :
A- 4-->5-->4-->9
B- 4-->7-->2-->10
C- 4-->7-->3
D- 4-->5-->8
Parmi les affirmations suivantes, laquelle décrit correctement un algorithme glouton pour rendre la monnaie ?
Réponses :
A- L'algorithme essaie toutes les combinaisons possibles afin d'utiliser le nombre de pièces minimal quel que soit le système de monnaie.
B- L'algorithme rend la monnaie en utilisant la plus grande pièce possible et en n'utilisant chaque valeur de pièces qu'une seule fois.
C- L'algorithme rend la monnaie en utilisant la plus grande pièce possible et en utilisant le nombre de pièces minimal quel que soit le système de monnaie.
D- L'algorithme rend la monnaie en utilisant la plus grande pièce possible et en utilisant le nombre de pièces minimal pour le système de monnaie européen, mais pas forcément pour d'autres systèmes.
On considère le problème où l’on doit rendre 10 euros de monnaie.
On dispose de pièces de 1,5,8 euros.
Indiquer le rendu de monnaie donné par un algorithme glouton.
Réponses :
A- 5 ; 5
B- 8 ; 1 ; 1
C- 5 ; 1 ; 1 ; 1 ; 1 ; 1
D- L'algorithme glouton échouera à rendre la somme de 10 euros.
Générateur aléatoire de questions sur les réseaux
Il faut actualiser la page pour changer de question. Propriétaire de la ressource : le site GeNumsi en licence CC BY_NC-SA
Savoirs et savoir-faire
-
la notion d'algorithme glouton,
-
qu'un algorithme glouton ne renvoie par forcément la solution optimale à un problème donné.
-
résoudre un problème grâce à un algorithme glouton,
-
implémenter un algorithme glouton donné,
-
améliorer un algorithme glouton donné.
Sitographie/Bibliographie

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International