Demander le programme !

Notion de parcours
Exemple introductif
Vous voici dans un lieu inconnu, un véritable dédale ! Vous voulez explorer complètement le lieu.
Par chance, vous disposez du plan suivant :
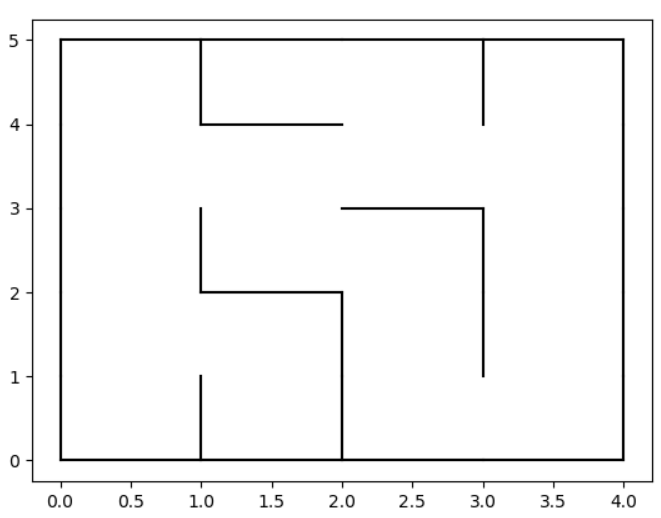
Vous comprenez que vous êtes au niveau du coin inférieur gauche de ce plan.
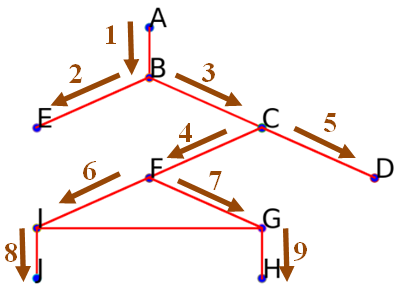
Afin de faciliter les explorations, vous décider de donner un nom, réduit à une lettre, à chaque intersection et cul-de-sac.
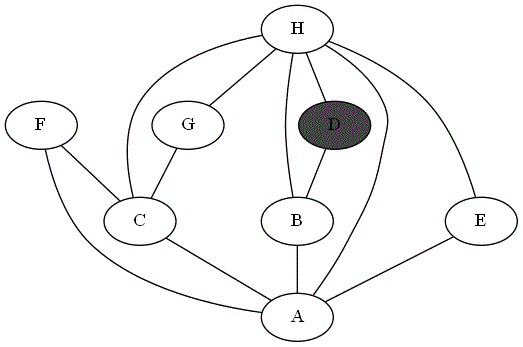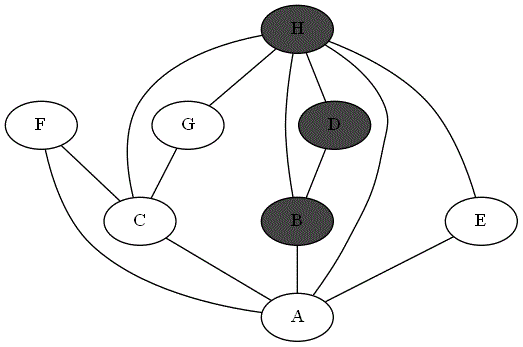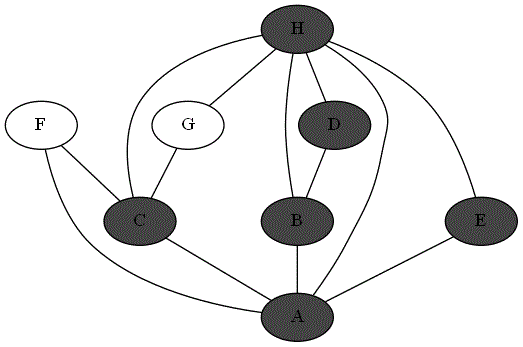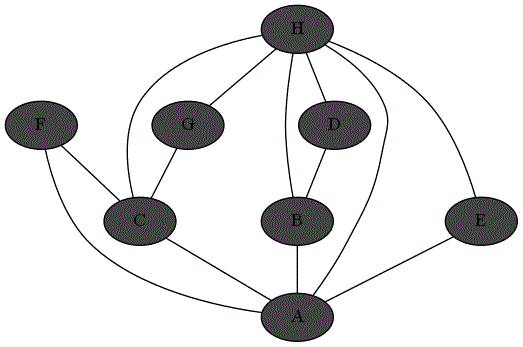
Vous obtenez donc le plan suivant, en sachant que vous êtes en $A$ initialement.
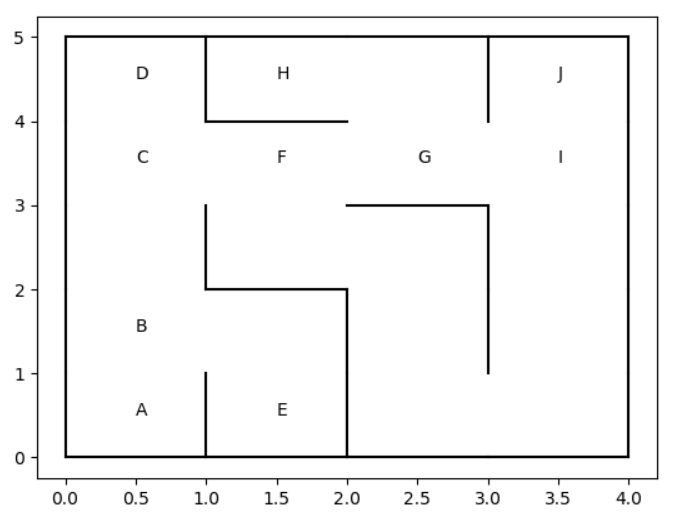
Plutôt que de voir le lieu comme un plan avec des lettres, on peut le modéliser par un graphe où :
-
chaque sommet correspond à une lettre représentant une intersection ou un cul-de-sac.
-
chaque arête correspond à un chemin direct entre les deux sommets.
Le lieu est donc modéliser par le graphe suivant :
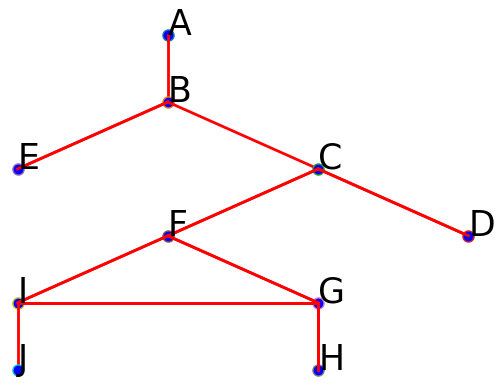
Explorer complètement le lieu, revient à passer par chaque sommet du graphe en visitant toutes les arêtes du graphes.
-
À quelle notion déjà vue vous fait penser ce graphe ?
-
En quoi ce graphe diffère de cette notion déjà vue ?
Notion de parcours
Voici ci-dessous une première définition :
Parcourir un graphe consiste à :
-
visiter chaque sommet du graphe une seule fois,
-
appliquer un même traitement en chaque sommet.
Considérons le labyrinthe d'introduction où l'entrée est en $A$.

Appliquons comme traitement constant le fait de toujours avancer en longeant les murs en faisant en sorte que la main droite reste collée à un mur.
Si on liste les sommets atteints successivement pour la première fois, on obtient :
['A', 'B', 'E', 'C', 'F', 'I', 'J', 'G', 'H', 'D'].
On a ainsi obtenu un parcours du graphe de racine 'A' :

-
Trouver un autre lieu de départ dans le labyrinthe tel qu'en se déplaçant en longeant les murs de sorte que la main droite reste collée à un mur, seule une partie du labyrinthe soit parcourue.
-
Comment modifier le labyrinthe pour qu'en partant du sommet 'A' avec un déplacement par une main droite posée contre un mur vous ne parcouriez plus qu'une partie du labyrinthe ?
-
Critiquer la définition écrite dans l'exemple précédent.
Obtenons désormais une définition plus précise :
Un parcours de racine $r$ est une liste $L$ de sommets telle que :
-
$r$ est le premier élément de la liste $L$,
-
chaque sommet du parcours apparaît une fois et une seule dans la liste $L$,
-
tout sommet, sauf la racine $r$, est adjacent à au moins un sommet placé devant lui dans la liste $L$.
Bien comprendre que le but d'un parcours est d'obtenir la liste de tous les sommets une seule fois.
-
['A', 'B', 'E', 'C', 'F', 'I', 'J', 'G', 'H', 'D']est bien un parcours de graphe de racine 'A' (vu précédemment) -
mais
['A', 'E', 'B', 'C', 'F', 'I', 'J', 'G', 'H', 'D']n'en est pas un car les sommets 'A' et 'E' ne sont pas adjacents.
On reprend le labyrinthe et son graphe :

|

|
-
Voici deux listes de sommets :
-
['A', 'B', 'E', 'I', 'J' ,'F', 'G', 'H', 'D', 'C'], -
['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J'].
Quelles listes parmi celles ci-dessus correspondent à un parcours du graphe ?
-
-
Proposer un autre parcours du graphe.
On peut retrouver le parcours obtenu à l'exemple 1 directement avec le graphe déjà obtenu :

Méthode : Descendre le plus profondément possible dans le graphe.
Une fois atteint un sommet sans arête menant à un sommet non encore visité
(comme par exemple l'équivalent d'une feuille d'un arbre), remonter au sommet
le plus proche où il existe une arête menant à un sommet non encore exploré.
Voici la succession des sommets obtenus en parcourant suivant cette méthode le graphe en partant du sommet $A$ :
-
Suivre l'arête menant à $B$ :
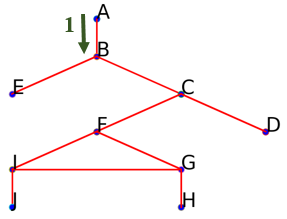 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B']. -
Suivre l'arête menant à $E$ (on pourrait aussi aller vers $C$):
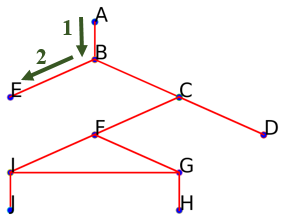 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E']. -
On ne peut aller plus profondément à partir de $E$ car toutes les arêtes y menant on déjà été parcourues.
Remonter au sommet précédent $E$ : $B$.
Comme il reste encore une arête reliant $B$ à un sommet non encore parcouru, suivre l'arête reliant $B$ à $C$ :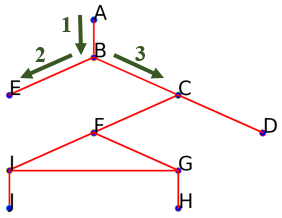 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C']. -
Suivre l'arête menant à $F$ (on pourrait aussi aller vers $D$):
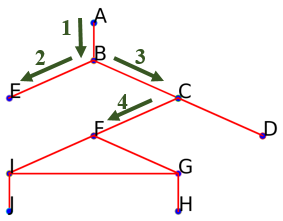 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F']. -
Suivre l'arête menant à $I$ (on pourrait aussi aller vers $G$):
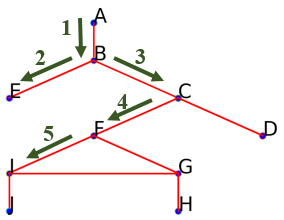 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F', 'I']. -
Suivre l'arête menant à $J$ (on pourrait aussi aller vers $G$) :
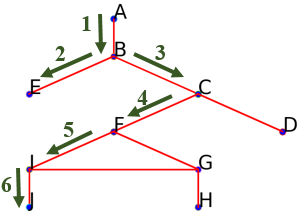 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F', 'I', 'J']. -
On ne peut aller plus profondément à partir de $J$ car toutes les arêtes y menant on déjà été parcourues.
Remonter au sommet précédant $J$ : $I$.
Comme il reste encore une arête reliant $I$ à un sommet non encore parcouru, suivre l'arête reliant $I$ à $G$ :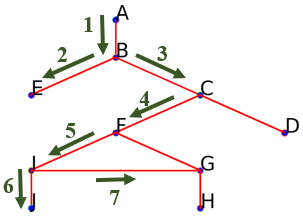 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F', 'I', 'J', 'G']. -
Suivre l'arête menant à $H$ (on ne prend pas l'arête vers $F$ car on est déjà passé par $F$):
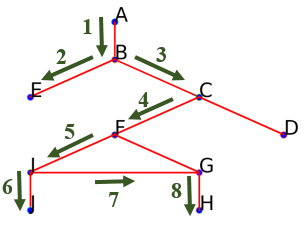 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F', 'I', 'J', 'G', 'H']. -
On ne peut aller plus profondément à partir de $H$ car toutes les arêtes y menant on déjà été parcourues.
Remonter au sommet précédant $H$ : $G$ ; cependant aucune arête liée à ce sommet ne permet d'atteindre un sommet non encore parcouru ($F$ a déjà été parcouru).
Remonter au sommet précédant $G$ : $I$ ; cependant aucune arête liée à ce sommet ne permet d'atteindre un sommet non encore parcouru.
Remonter au sommet précédant $I$ : $F$ ; cependant aucune arête liée à ce sommet ne permet d'atteindre un sommet non encore parcouru.
Remonter au sommet précédant $F$ : $C$.
Comme il reste encore une arête reliant $C$ à un sommet non encore parcouru, suivre l'arête reliant $C$ à $D$ :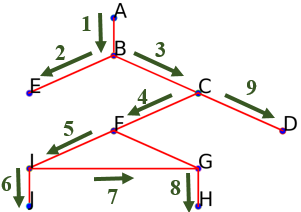 On obtient aussi le parcours suivant :
On obtient aussi le parcours suivant : ['A', 'B', 'E', 'C', 'F', 'I', 'J', 'G', 'H', 'D']. -
On ne peut aller plus profondément à partir de $D$ car toutes les arêtes y menant ont déjà été parcourues.
Remonter au sommet précédant $D$ : $C$ ; cependant aucune arête liée à ce sommet ne permet d'atteindre un sommet non encore parcouru.
En remontant ainsi, aucun sommet atteint n'est relié à un sommet non encore parcouru : il ne reste plus de sommets à découvrir. on a donc fini de parcourir le graphe.
On obtient aussi aboutit au parcours suivant :['A', 'B', 'E', 'C', 'F', 'I', 'J', 'G', 'H', 'D'].
Il est possible de modéliser le labyrinthe par un autre graphe. On obtiendrait ainsi un autre parcours ; les sommets seraient identiques mais leur ordre d'apparition différerait.
Un parcours de graphe n'est pas unique.

Refaire le parcours à partir de ce graphe en choisissant de partir vers le sommet de "droite" à chaque "intersection".
Voici ci-dessous un graphe orienté.
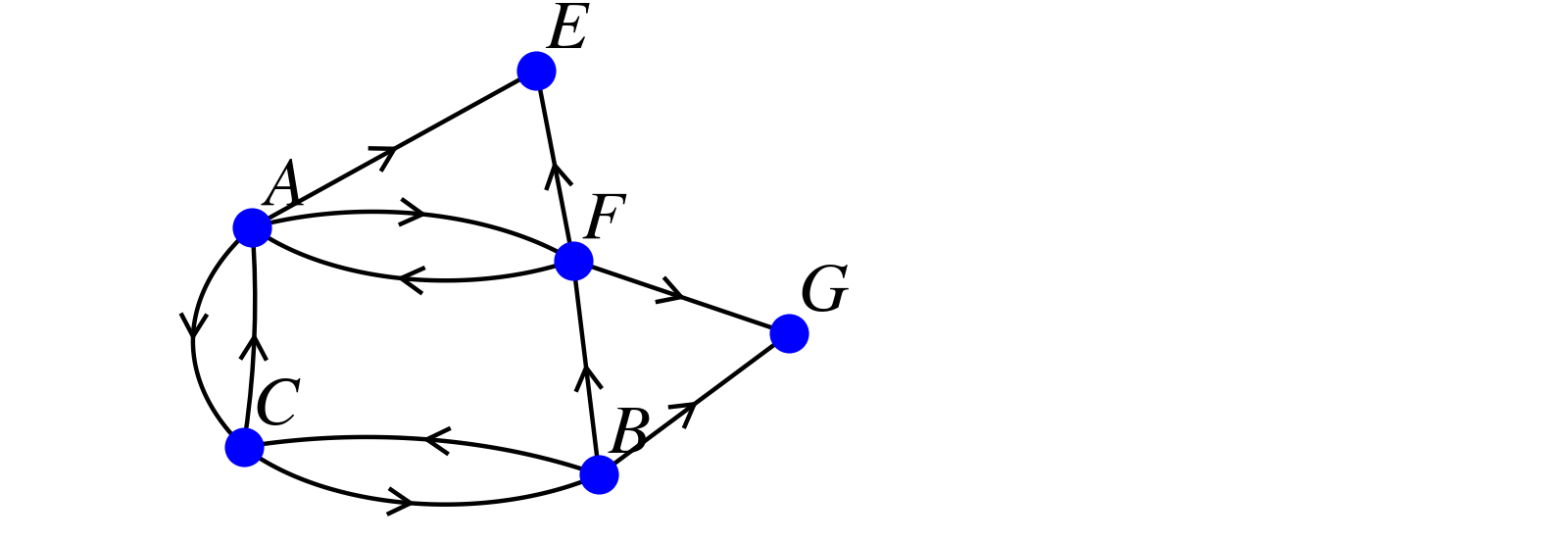
-
Proposer un dictionnaire en Python qui permet d'implémenter la liste d'adjacence du graphe orienté ci-dessus.
-
Proposer un script qui récupère tous les sommets du graphe orienté précédent sans doublon. Le tester sur le graphe précédent.
-
Est-ce que le script précédent qui renvoie l'ensemble des sommets une unique fois renvoie toujours un parcours ?
Attention à ne pas confondre liste de tous sommets apparaissant une seule fois et parcours !
Un parcours doit aussi vérifier la condition : tout sommet, sauf la racine , doit être adjacent à au moins un sommet placé devant lui dans la liste définissant le parcours.
Parcours en profondeur
Vision naïve
Le parcours en profondeur revient à ce que vous feriez si un jour vous vous retrouviez perdu.e.s dans un lieu inconnu que vous désirez découvrir (un désir vraiment très profond !) :
-
vous essayez un chemin,
-
si vous êtes coincé.e.s, vous faites demi-tour jusqu'à ce que vous reveniez à une intersection menant à une partie non encore explorée
-
Quand il ne reste plus d'intersection menant à une partie non encore explorée, vous avez terminé de parcourir le lieu : tout a été découvert !
Le parcours en profondeur correspond à la stratégie de parcours de graphe suivante :
en visitant un voisin $v$ d'un sommet $u$, on visite d'abord les voisins de $v$ avant de visiter les
autres voisins de $u$.
Comment l'implémenter ?
Sans chercher à comprendre pour l'instant tous les détails, lors de l'exploration :
-
on cherche à toujours prolonger le chemin : on rajoute un lieu non encore visité : on "empile" donc les lieux les uns après les autres .
-
Lors d'un cul-de-sac où l'on est coincé, on rebrousse chemin : on "dépile" à partir du dernier visité.
On retrouve bien le principe dernier lieu rajouté, premier lieu retiré : c'est le principe d'une pile.
L'implémentation d'un parcours en profondeur se fait à l'aide d'une pile.
Pour se souvenir de ce qui a déjà été exploré du reste, il est important de "marquer" tout endroit exploré afin de ne pas les visiter à nouveau. En pratique, dans un labyrinthe, si on a la chance d'avoir une craie, on peut écrire une marque ou colorier en partie un endroit.
Cette exploration pour tout découvrir du lieu peut s'écrire sous forme d'algorithme en langage naturel :
A. Chercher un endroit non encore visité B. Puis marquer cet endroit nouvellement visité C. Ensuite étudier les lieux voisins de cet endroit ; trois possibilités : cas 1 : si le lieu voisin a déjà été exploré (car marqué), on l'ignore, cas 2 : si le lieu voisin n'a pas encore été visité, je le visite : on recommence alors le B. cas 3 : lorsque tous les voisins ont été visités : cet endroit n'a plus d'intérêt : on revient à l'endroit précédant celui actuel et on recommence le C. D. On continue ainsi tant qu'il reste des lieux à visiter.
Quelle(s) partie(s) de l'algorithme permet(tent) d'obtenir possiblement plusieurs parcours différents à partir du même sommet ?
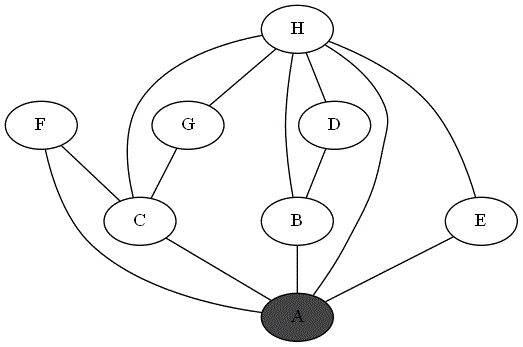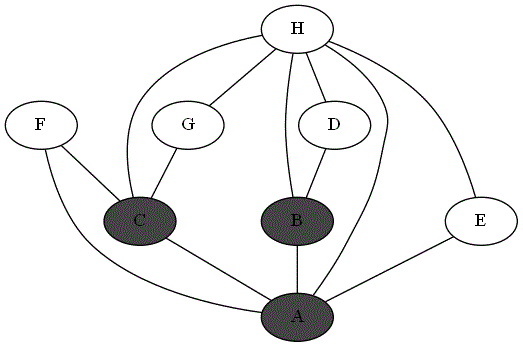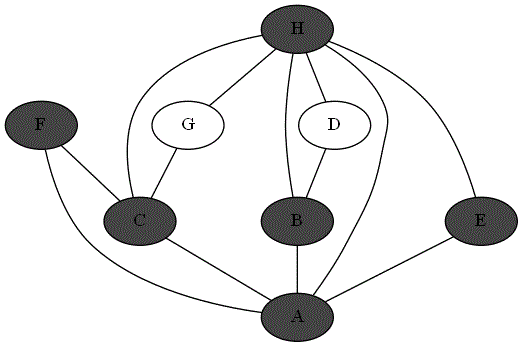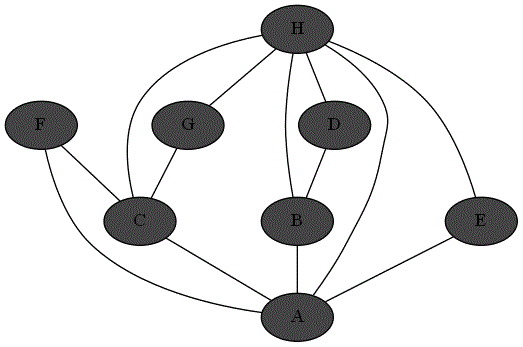
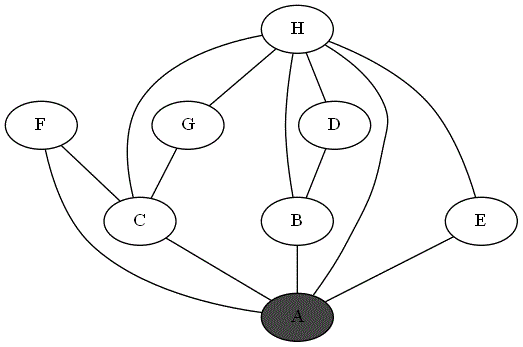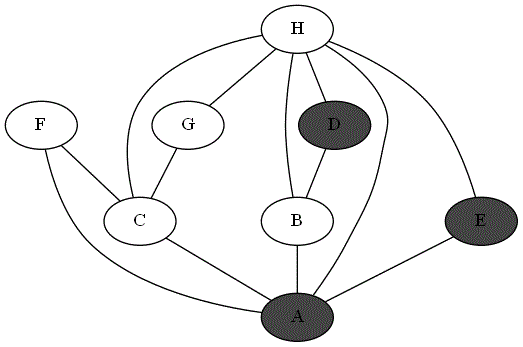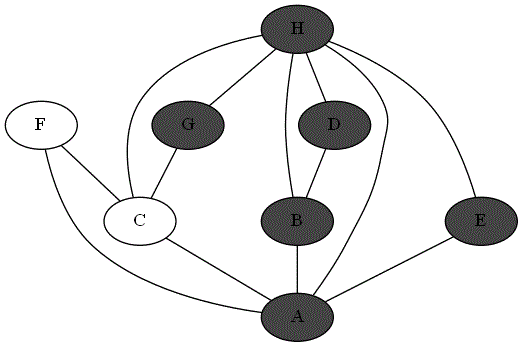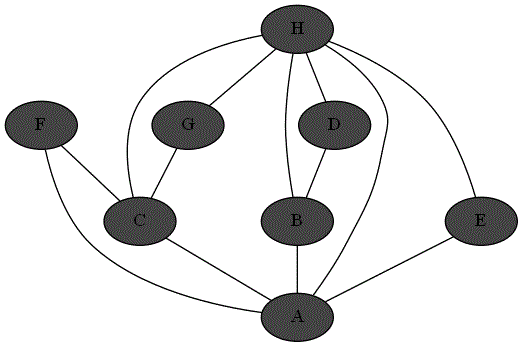
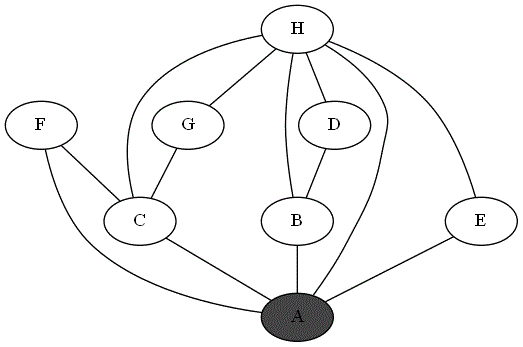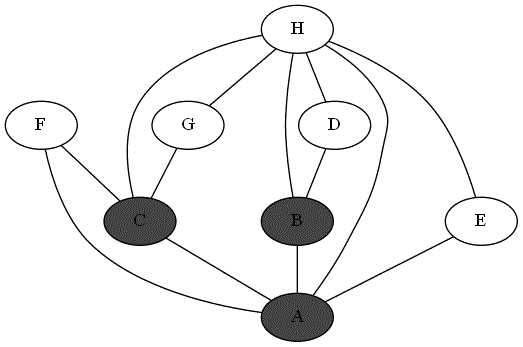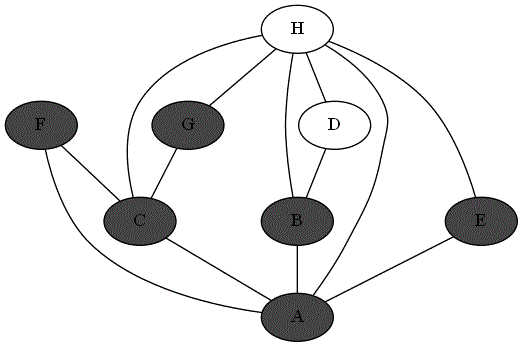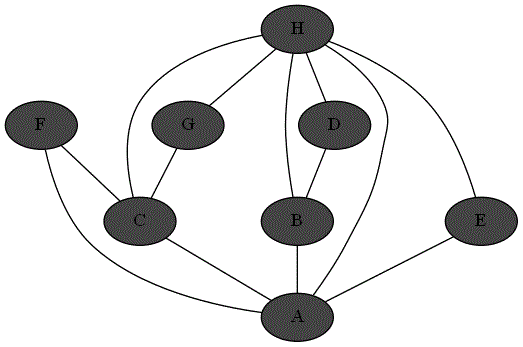
Quatre animations ci-dessous représentent 4 parcours différents sur le même graphe à partir du sommet 'A'.
-
Repérer le parcours qui correspond bien à un parcours en profondeur du graphe à partir du sommet
'A'. -
Expliquer pourquoi les autres parcours ne sont pas un parcours en profondeur du graphe à partir du sommet
'A'.
Parcours 1 :
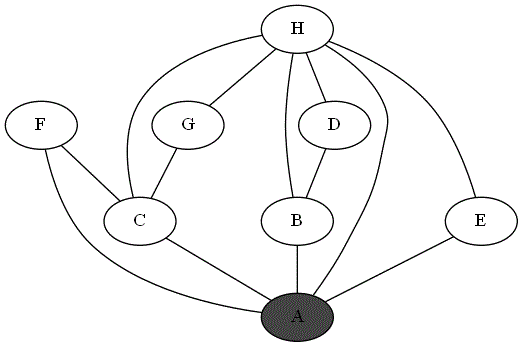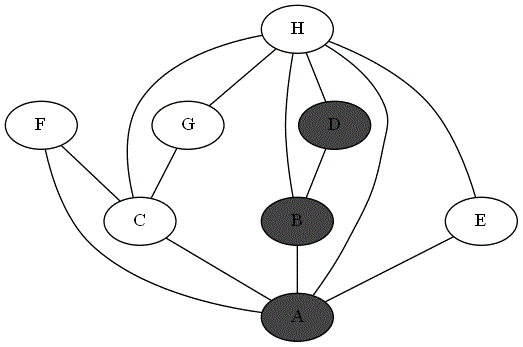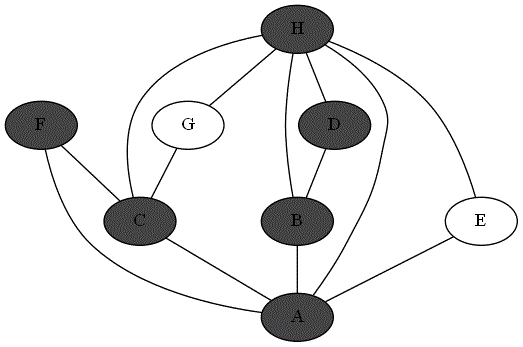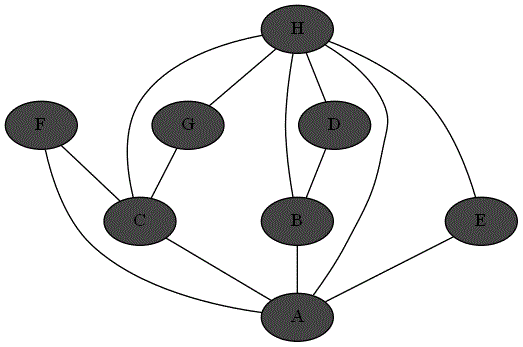
Parcours 2 :
Parcours 3 :
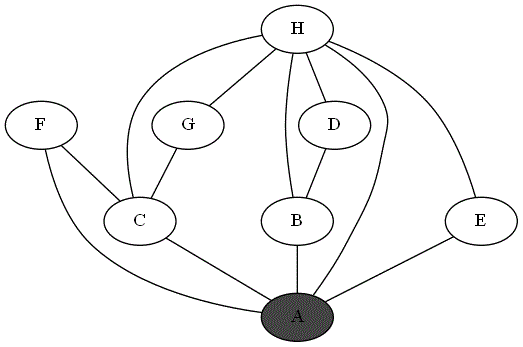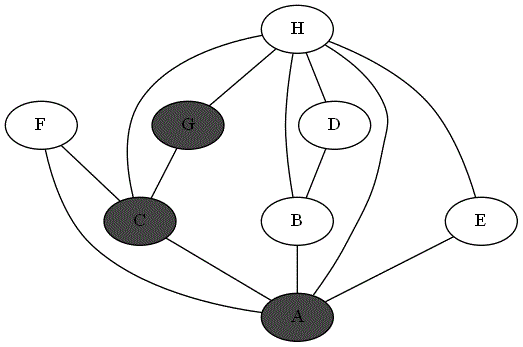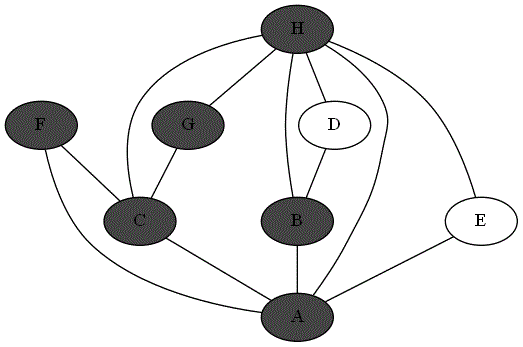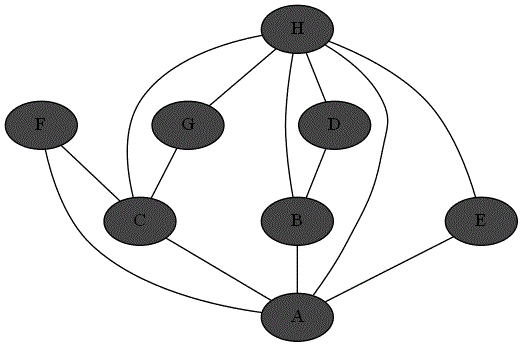
Parcours 4 :
Plusieurs algorithmes sont construits sur ce principe de parcours en profondeur.
Algorithme en récursif
Nous allons maintenant réécrire la vision naïve précédente sous forme d'une procédure récursive en pseudo-code en utilisant le vocabulaire des graphes à la place de celui de lieux comme un labyrinthe :
parcourir_profondeur(graphe, sommet) : Marquer le sommet comme visité et l'afficher Pour chaque voisin du sommet passé en paramètre Si le voisin n'est pas marqué visité parcourir_profondeur(graphe, voisin)
-
Pourquoi est-ce bien une procédure récursive ?
-
Pourquoi est-on certain que cette procédure s'arrête à un moment ?
Attention ! On ne marque un sommet (pour ne plus chercher à aller le visiter) non parce qu'il a déjà été rencontré comme voisin mais lorsqu'on le visite réellement : il ne faut alors chercher à le (re)visiter.
On sait qu'il est possible d'implémenter un graphe en prenant un dictionnaire pour définir sa liste d'adjacence.
Devant tant d'efforts pour comprendre les parcours, vous rêvez de partir en voyage sur le continent sud-américain. Mais quel parcours effectuer pour visiter tous les pays de l'Amérique du Sud ?
Vous allez dans cet exercice :
-
utiliser un graphe implémenté comme dictionnaire avec la liste des successeurs, représentant les pays frontaliers d'Amérique du Sud,
-
programmer un parcours en profondeur,
-
l'appliquer au voyage de votre rêve !
Voici la carte des pays du continent sud-américain :
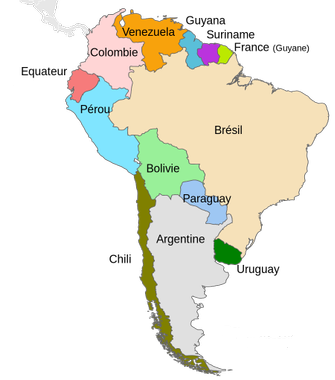
On considère le dictionnaire suivant qui permet d'associer à chaque pays d'Amérique du Sud la liste des pays partageant une frontière terrestre.
G = {} #ou dict() mais plus coûteux
G["France"] = ["Bresil", "Suriname"]
G["Argentine"] = ["Bolivie", "Bresil", "Chili", "Paraguay", "Uruguay"]
G["Bolivie"] = ["Argentine", "Bresil", "Chili", "Paraguay", "Perou", "Uruguay"]
G["Bresil"] = ["Argentine", "Bolivie", "Colombie", "France", "Guyana", "Paraguay", "Perou", "Suriname", "Uruguay", "Venezuela"]
G["Chili"]=["Argentine", "Bolivie", "Perou"]
G["Colombie"] = ["Bresil", "Equateur", "Perou", "Venezuela"]
G["Equateur"] = ["Colombie", "Perou"]
G["Guyana"] = ["Bresil", "Suriname", "Venezuela"]
G["Paraguay"] = ["Argentine", "Bolivie", "Bresil"]
G["Perou"] = ["Bolivie", "Bresil", "Chili", "Colombie", "Equateur"]
G["Suriname"] = ["Bresil", "France", "Guyana"]
G["Uruguay"] = ["Argentine", "Bolivie", "Bresil"]
G["Venezuela"] = ["Bresil", "Colombie", "Guyana"]
Pour savoir quels sommets ont déjà été visités ou non, vous allez utiliser un dictionnaire dont les clés seront les sommets du graphe et les
valeurs associées seront les chaînes de caractères soit "inconnu", soit "visite"
-
Créer une fonction
initialiserqui prend comme paramètre un graphe et renvoie un dictionnaire dont les clés sont les sommets du graphe et la valeur est toujours"inconnu".
Créer une fonction visiter qui prend comme paramètre le dictionnaire associant à chaque sommet
son état de connaissance et un sommet du graphe, fonction qui renvoie le dictionnaire de connaissance où la
valeur associée au sommet entré est mise à 'visite'
Écrire en langage Python la procédure récursive parcours_longueur_rec correspondant à un parcours en
profondeur en faisant aussi en sorte que chaque sommet qui vient d'être marqué soit affiché.
Cette procédure prend trois arguments : un graphe, un sommet de ce graphe, sommet servant de point de départ
au parcours et un dictionnaire associant à chaque sommet du graphe sont état
('inconnu' ou 'visite')
Gérer l'affichage à l'aide de l'instruction print.
Vérifier que votre procédure parcours_longueur_rec appliquée au sommet "Bolivie" conduit au parcours
visualisable avec l'animation ci-dessous :
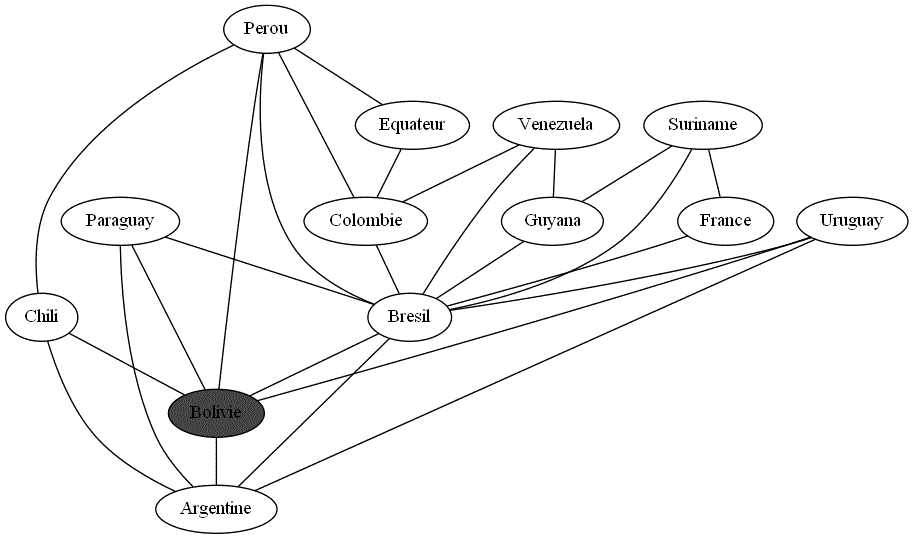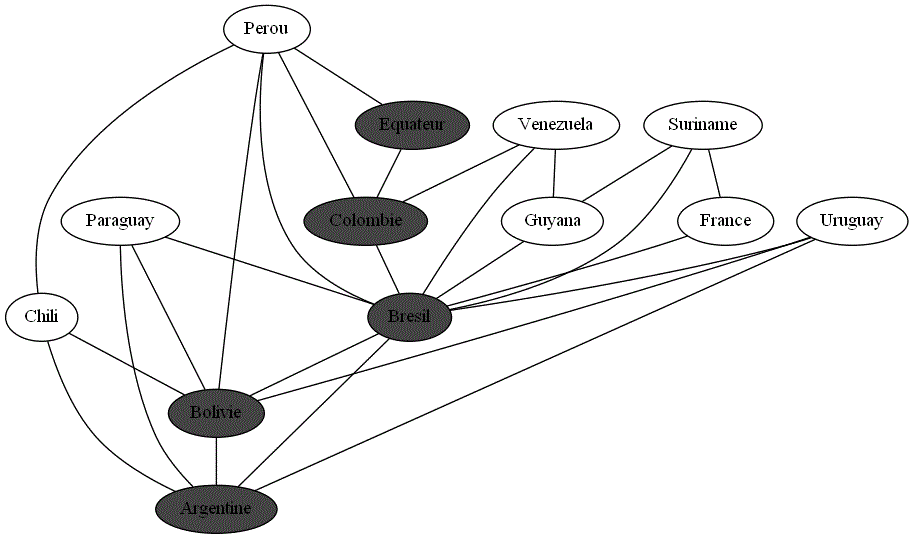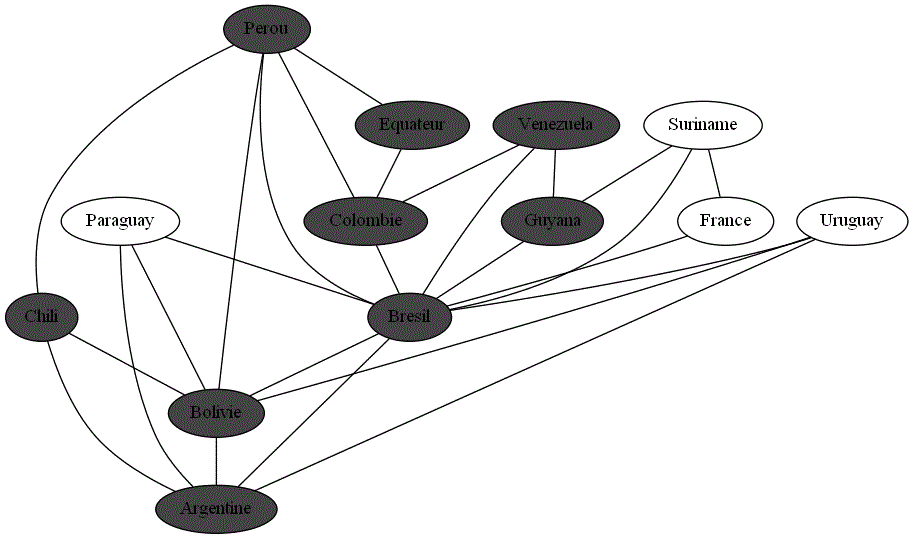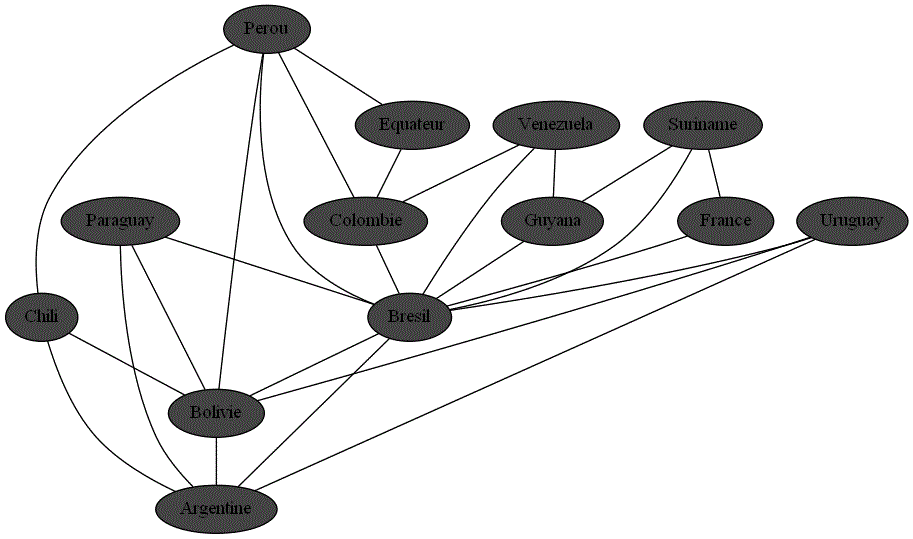
Appliquer cette procédure au graphe modélisant les pays d'Amérique du Sud en prenant comme racine, c'est-à-dire sommet de départ la France (pour la Guyane Française). À la lecture de tous les pays que vous allez visiter, vous allez être profondément heureux.ses.
Les dictionnaires Python sont ordonnés depuis la version 3.7 pour garantir justement que les parcours s'effectuent dans le même ordre sur toutes les machines. Si vous travaillez avec une version plus ancienne, téléchargez une version récente.
La complexité en temps d'un parcours en profondeur est en $O(n+m)$, où $m$ désigne le nombre d'arêtes du graphes et $n$ le nombre de sommets.
En effet, chacun des $n$ sommets sera traité une seule fois. Mais à partir de chaque sommet, on itère sur les voisins donc $O(n)$ ne suffit pas : il faut prendre aussi en compte le nombre $m$ d'arêtes.
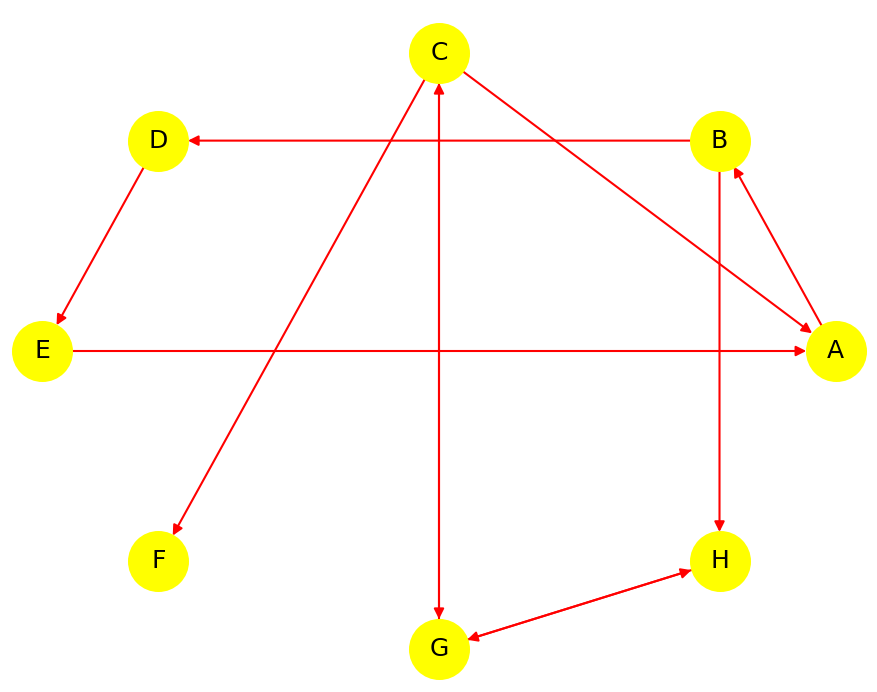
Nous allons désormais dans cet exercice travailler dans le cas d'un graphe orienté. Considérons, par exemple le graphe suivant :
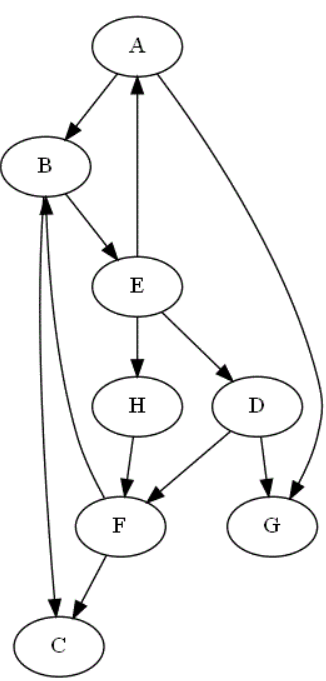
-
Proposer un parcours en profondeur de graphe à partir du sommet 'A'.
Voici ci-dessous le dictionnaire permettant de définir le graphe :
graphe_or = {'A': ['B', 'G'],
'B': ['C', 'E'],
'D': ['F','G'],
'E': ['A', 'D', 'H'],
'F': ['B','C'],
'H': ['F']
}
Utiliser le script obtenu dans l'exercice précédent sur ce graphe. Que remarquez-vous ?
Expliquer la raison de ce que vous venez de remarquer.
Proposer une correction du script incluant les fonctions initialiser
et parcours_longueur_rec afin de le rendre fonctionnel avec un graphe orienté ayant au moins un sommet n'ayant aucun successeur.
Tester le script modifié pour obtenir un parcours en profondeur du graphe à partir du sommet 'A'.
Il est possible de traiter plus simplement le cas où le sommet n'est pas une clé du dictionnaire
graphe en utilisant la méthode get s'appliquant sur les dictionnaires.
À la place des deux lignes if s in graphe.keys(): for voisin in graphe[s]:, il suffit d'écrire
for voisin in graphe.get(s, []).
En effet :
-
Dans le cas où
sest un sommet du graphe défini comme clé, alorsgraphe.get(s, [])renvoie la valeur associée àsdans le dictionnairegraphe; c'est un équivalent àgraphe[s]. -
Dans le cas où
sn'est un sommet du graphe défini comme clé, alorsgraphe.get(s, [])renvoie[](le second argument).
Voici un exercice à faire en autonomie pour tester votre maîtrise
sur l'implémentation d'un parcours en longueur en récursif d'un graphe.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Ne pas hésiter à compléter la version à trous !
On peut obtenir un résultat similaire en utilisant un module dédié aux graphes : networkx. C'est le but de l'exercice suivant :
Vous allez dans cet exercice :
-
obtenir, avec le module
networkx, un graphe représentant les pays frontaliers d'Amérique du Sud, ainsi qu'une représentant de ce graphe grâce àmatplotlib.pyplot. -
programmer un parcours en profondeur,
-
l'appliquer au voyage de votre rêve !
Voici la carte des pays du continent sud-américain :

-
Télécharger le programme en langage Python. Le graphe non-orienté modélisant la carte a :
-
pour sommets les États,
-
pour arêtes toute frontière commune entre deux États.
-
-
Le module
networkxpermet d'implémenter d'une autre manière le graphe.
Voici quelques indications sur des méthodes denetworkxen considérant un graphe nommégrapheet un sommet nommés:-
La méthode
nodes()renvoie sous forme d'un itérable l'ensemble des sommets du graphegraphe.
sommets = graphe.nodes()stocke dans une variablesommetsl'ensemble des sommets du graphegraphe. -
Avec
networkx, il est possible d'associer à tout sommet d'un graphe un dictionnaire d'attributs.
attributs_sommet = graphe.nodes[s]stocke dans une variableattributs_sommetle dictionnaire des attributs du sommetsappartenant au graphegraphe. -
attributs_sommet(défini comme ci-dessus) étant un dictionnaire, vous pouvez alors ajouter toute nouvelle association à celui-ci en utilisant les méthodes vues sur les dictionnaires :
attributs_sommet["new_attribut"] = new_valpermet de rajouter à l'objet sommet nommésommetdu graphe l'attribut nommé icinew_attributen spécifiant sa valeur associée, icinew_val.
Aidez-vous des deux indications précédentes afin de créer une procédure
marquerqui :-
prend comme argument un graphe
grapheimplémenté sousnetworkxet un sommets(que l'on admet être de ce graphe), -
créé dans le dictionnaire des attributs en lien avec le sommet
sun attribut nommé"visite"associé à la valeurTrue.
-
-
Voici une nouvelle méthode de
networkxs'appliquant sur un objet graphe nommé icigrapheet qui prend comme paramètre un sommet nommés:
graphe.neighbors(s)renvoie un ensemble itérable contenant tous les sommets voisins du sommetsdu graphegraphe.Écrire en langage Python à l'aide du module
networkxla procédure récursive correspondant à un parcours en profondeur en faisant aussi en sorte que chaque sommet qui vient d'être marqué soit affiché.Gérer l'affichage à l'aide de l'instruction
print. -
Appliquer cette procédure au graphe modélisant les pays d'Amérique du Sud en prenant comme racine, c'est-à-dire sommet de départ la France (pour la Guyane Française). À la lecture de tous les pays que vous allez visiter, vous allez être profondément heureux.ses.
Voici désormais une variante colorée de l'algorithme précédent :
Le changement avec la version précédente réside surtout dans le marquage des sommets.
Au lieu d'avoir deux états marqués visite ou non visite, on considère trois états :
-
initialement tous les sommets sont en blanc,
-
tout sommet rencontré pour la première fois sera mis en gris,
-
lorsque tous les successeurs d'un sommet ont été visités, ce sommet est mis en noir.
Voici cette variante de l'algorithme de parcours en profondeur en langage naturel :
// Fonction principale parcourir_profondeur(graphe G) : // coloration initiale des sommets du graphe pour chaque sommet s du graphe G faire mettre la couleur du sommet s en blanc // coloration liée au parcours pour chaque sommet s du graphe G faire si la couleur du sommet s est en blanc alors visiter les voisins en profondeur de s par appel à la fonction visiter_profondeur(graphe G, sommet s) // fonction utilisée pour visiter les voisins en profondeurs d'un sommet visiter_profondeur(graphe G, sommet s) : mettre la couleur du sommet s en gris afficher le sommet s pour chaque voisin v du sommet s faire // cas de l'existence d'un voisin non encore visité si la couleur du voisin v est blanc alors visiter les voisins en profondeur de v par appel à la fonction visiter_profondeur(graphe G, sommet v) // une fois tous les successeurs visités mettre la couleur du sommet s en noir
En quoi l'algorithme écrit ci-dessus en langage courant est-il un algorithme récursif ?
Dans tout cet exercice, vous travaillerez avec le graphe G défini par le dictionnaire suivant :
G = {}
G["France"] = ["Bresil", "Suriname"]
G["Argentine"] = ["Bolivie", "Bresil", "Chili", "Paraguay", "Uruguay"]
G["Bolivie"] = ["Argentine", "Bresil", "Chili", "Paraguay", "Perou", "Uruguay"]
G["Bresil"] = ["Argentine", "Bolivie", "Colombie", "France", "Guyana", "Paraguay", "Perou", "Suriname", "Uruguay", "Venezuela"]
G["Chili"]=["Argentine", "Bolivie", "Perou"]
G["Colombie"] = ["Bresil", "Equateur", "Perou", "Venezuela"]
G["Equateur"] = ["Colombie", "Perou"]
G["Guyana"] = ["Bresil", "Suriname", "Venezuela"]
G["Paraguay"] = ["Argentine", "Bolivie", "Bresil"]
G["Perou"] = ["Bolivie", "Bresil", "Chili", "Colombie", "Equateur"]
G["Suriname"] = ["Bresil", "France", "Guyana"]
G["Uruguay"] = ["Argentine", "Bolivie", "Bresil"]
G["Venezuela"] = ["Bresil", "Colombie", "Guyana"]-
En modifiant la procédure
marquerfaite dans le précédent exercice sur où l'implémentation était un dictionnaire, créer une fonctioncolorierqui a quatre paramètres :-
grapheun graphe (que l'on considérera comme un dictionnaire), -
sun sommet du graphegraphe, -
coulune chaîne de caractères valant soit"blanc","gris"ou"noir -
couleurun dictionnaire associant à chaque sommet du graphe une couleur.
Cette procédure renvoie un dictionnaire qui associe à chaque sommet une
"couleur"pouvant être :"blanc","gris"ou"noir. -
-
Créer une procédure
parcourir_profondeurqui prend en paramètres un graphe, nommégrapheimplémenté par un dictionnaire.
Cette procédure fera appel à la procédurevisiter_profondeurque vous construirez à la question suivante. -
Créer une procédure
visiter_profondeurqui prend en paramètres un graphe, nommégraphe, implémenté par un dictionnaire, un sommet de ce graphe nommésommetet un dictionnairecouleurqui associe
-
Tester cet algorithme de parcours en profondeur avec trois colorations en prenant le graphe sur les pays d'Amérique du Sud.
Comparer les affichages obtenus avec les deux versions du parcours en profondeur en version récursive vues dans cette partie.
-
En modifiant la procédure
marquerfaite dans le précédent exercice sur networkx, créer une procédurecolorierqui a trois paramètres :-
grapheun graphe (que l'on considérera comme objet de la classeGraph()du modulenetworkx), -
sun sommet du graphegraphe, -
coulune chaîne de caractères valant soit"blanc","gris"ou"noir
Les sommets se voient avec cette procédure rajouter un attribut nommé
"couleur"pouvant prendre, outreNone, trois valeurs :"blanc","gris"ou"noir.sommet["attribut"] = valeurOn peut rajouter à l'objet sommet nommé
sommetdu graphe n'importe quel attribut nommé iciattributet spécifier lavaleurde cette attribut. -
-
Créer une procédure
parcourir_profondeurqui prend en paramètres un graphe, nommégraphe.
Cette procédure fera appel à la procédurevisiter_profondeurque vous construirez à la question suivante.Comme lors de l'exercice de programmation précédent, vous pouvez utiliser les méthodes suivantes :
Voici quelques indications sur des méthodes de
networkxen considérant un graphe nommégrapheet un sommet nommés:-
liste_sommets = graphe.nodes()La méthode
nodes()renvoie sous forme de liste l'ensemble des sommets du graphegraphe. -
attributs_sommet = graphe.nodes[s]graphe.nodes[s]renvoie, sous forme de dictionnaire, les attributs du sommetsdu graphegraphe. -
attributs_sommet.get("attribut")permet d'obtenir (d'accéder) à la valeur de l'attribut
"attribut""du dictionnaire nomméattributs_sommet.La méthode
getpermet d'obtenir la valeur associée à la clé donnée comme argument ; plus précisémentdico.get(cle):-
si la clé
cleexiste dans le dictionnairedicoalors il y a renvoi de la valeur associée (comme le feraitdico[cle]). -
Si cette clé
clen'existe pas dans le dictionnaire, une nouvelle associationcle: Noneest ajoutée au dictionnaire (sans lever une exception du typeKeyError), -
Il est possible de rajouter un deuxième paramètre qui sera la valeur par défaut de la clé
clelors du rajout de la nouvelle association de clécle.
-
-
-
Créer une procédure
visiter_profondeurqui prend en paramètres un graphe, nommégrapheet un sommet de ce graphe nommésommet.
graphe.neighbors(s)renvoie la liste de tous les sommets voisins du sommet
sdu graphegraphe. -
Tester cet algorithme de parcours en profondeur avec trois colorations en prenant le graphe sur les pays d'Amérique du Sud.
Comparer les affichages obtenus avec les deux versions du parcours en profondeur en version récursive vues dans cette partie.
Algorithme en itératif
L'algorithme en récursif d'un parcours en profondeur risque un débordement de la pile d'appel si cet algorithme est employé sur un graphe avec de nombreux sommets. Afin d'éviter cela, il peut être utile de programmer directement en itératif.
Nous avons déjà vu au 3.1. que "naturellement" l'implémentation d'un algorithme de parcours en profondeur se fait à l'aide d'une pile. Cette pile servira à remplacer la pile d'appel de la version récursive.
Dans cette pile seront stockés temporairement l'ensemble des sommets non encore visités.
Voici en langage naturel, une fonction donnant un parcours en profondeur en itératif :
fonction parcours_profondeur_iteratif(Graphe G, sommet s)
Créer la liste visites des sommets déjà visités, liste réduite pour l'instant au sommet s
Créer reste_a_voir une pile vide
Ajouter les voisins du sommet s à la pile reste_a_voir (=empiler)
Tant que la pile reste_a_voir n'est pas vide faire :
dépiler la tête de la pile reste_a_voir et la stocker dans une variable u
si u ne fait pas partie de la liste des sommets déjà visités faire :
Rajouter u à la liste visite des sommets déjà visités
Pour tout sommet voisin v du sommet u faire :
si v ne fait pas partie de la liste des sommets déjà visités faire :
Ajouter le sommet v à la pile reste_a_voir
renvoyer la liste visites des sommets visités
-
Proposer un script en langage Python qui implémente la fonction
parcours_profondeur_iteratifoù graphe est défini par un dictionnaire donnant la liste d'adjacence.Pour l'instant, on suppose le graphe non-orienté.
-
Penser à utiliser
liste[-1]pour obtenir le dernier élément de la listeliste. -
Penser à utiliser la méthode
poppour supprimer un élément d'une liste dont la position est connue tout en renvoyant l'élément supprimé.
-
-
-
Tester la fonction précédente avec le graphe suivant :
G = {} G["France"] = ["Bresil", "Suriname"] G["Argentine"] = ["Bolivie", "Bresil", "Chili", "Paraguay", "Uruguay"] G["Bolivie"] = ["Argentine", "Bresil", "Chili", "Paraguay", "Perou", "Uruguay"] G["Bresil"] = ["Argentine", "Bolivie", "Colombie", "France", "Guyana", "Paraguay", "Perou", "Suriname", "Uruguay", "Venezuela"] G["Chili"]=["Argentine", "Bolivie", "Perou"] G["Colombie"] = ["Bresil", "Equateur", "Perou", "Venezuela"] G["Equateur"] = ["Colombie", "Perou"] G["Guyana"] = ["Bresil", "Suriname", "Venezuela"] G["Paraguay"] = ["Argentine", "Bolivie", "Bresil"] G["Perou"] = ["Bolivie", "Bresil", "Chili", "Colombie", "Equateur"] G["Suriname"] = ["Bresil", "France", "Guyana"] G["Uruguay"] = ["Argentine", "Bolivie", "Bresil"] G["Venezuela"] = ["Bresil", "Colombie", "Guyana"]
-
-
Utiliser la représentation du graphe ci-dessous pour savoir si la liste renvoyée dans le cas où l'on prend comme sommet initial
"Bolivie"correspond bien à un parcours en profondeur.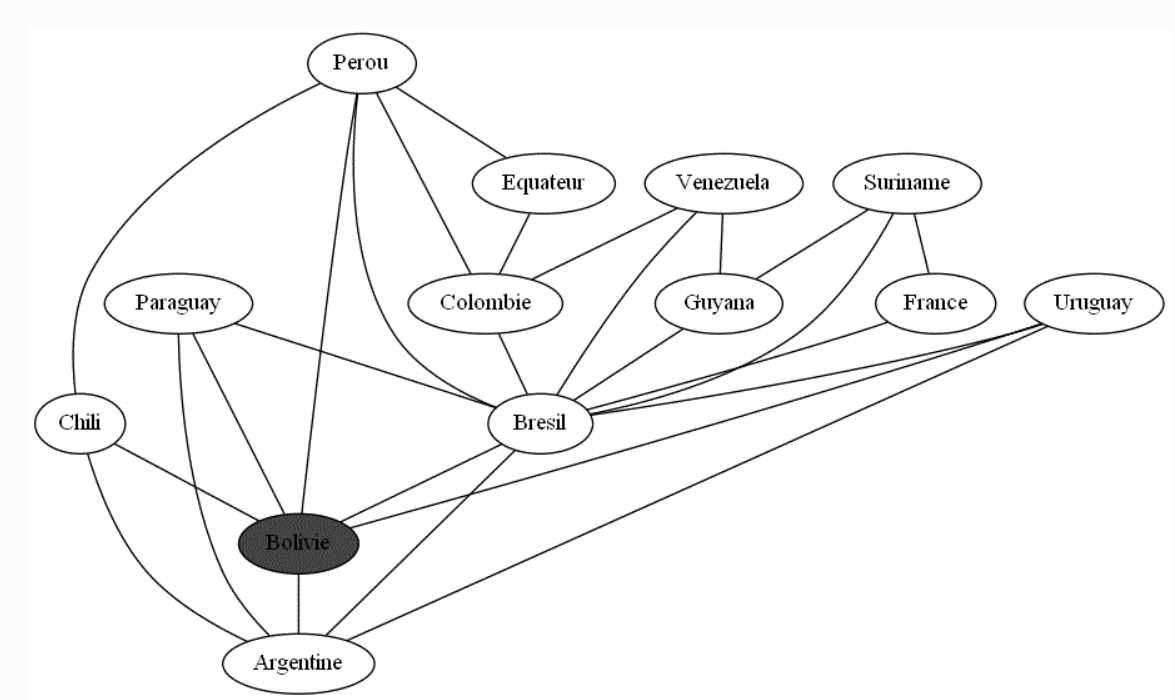
-
Est-ce que le parcours en profondeur obtenu avec cet algorithme itératif dans le cas où l'on prend comme sommet initial
"Bolivie"correspond bien au parcours en profondeur obtenu dans le cas récursif et qui est représenté dans le gif ci-dessous ?
-
Comment pouvez-vous expliquer cette différence en comparant les deux algorithmes récursifs et itératifs ?
-
Corriger le script précédent afin que le parcours renvoyé par la fonction
parcours_profondeur_iteratifsoit identique à celui en récursif.
Modifier la fonction parcours_profondeur_iteratif obtenue dans l'exercice précédent
dans le cas où le graphe peut être orienté.
Vous pouvez tester votre script an utilisant ce graphe orienté :
graphe_or = {'A': ['B', 'G'],
'B': ['C', 'E'],
'D': ['F', 'G'],
'E': ['A', 'D', 'H'],
'F': ['B', 'C'],
'H': ['F']
} -
En s'inspirant de vos travaux effectués ici, modifier la fonction
parcours_profondeur_iteratifobtenue dans l'exercice précédent en utilisant un dictionnaire qui associe à chaque sommet une valeur'inconnu'ou'visite'. -
En comparant la complexité de la fonction
parcours_profondeur_iteratifutilisant une liste des sommets déjà visités celle ci-dessus utilisant un dictionnaire qui associe à chaque sommet une valeur'inconnu'ou'visite', quelle implémentation semble préférable ?
Dans cet exercice, vous pouvez reprendre des éléments déjà obtenus à l'exercice de la première version récursive du parcours en profondeur comme ceux-ci :
-
vous prendrez une liste Python en guise de pile en considérant que le sommet de la pile correspond au dernier élément de la liste.
-
Le graphe sera supposé être un objet de la classe
Graph()de la bibliothèqueNetworkx; ceci permettra d'utiliser les méthodes de cette bibliothèque comme par exemple :-
graphe.neighbors(v)qui permet d'obtenir les voisins d'un sommetvdu graphegraphe, -
vous pourrez transtyper en liste l'itérable des voisins d'un sommet donné grâce à
list.
-
-
Écrire en langage Python une fonction
parcours_profondeur_iteratifqui correspond à la fonction vue ci-dessus en langage naturel.-
Penser à utiliser
liste[-1]pour obtenir le dernier élément de la listeliste. -
Penser à utiliser la méthode
poppour supprimer un élément d'une liste dont la position est connue tout en renvoyant l'élément supprimé.
-
-
Tester cet algorithme de parcours en profondeur en prenant le graphe sur les pays d'Amérique du Sud.
-
En vous aidant de la carte de l'Amerique du Sud ci-dessous, vérifier que la liste renvoyée correspond bien à un parcours en profondeur.

Voici un exercice à faire en autonomie pour tester votre maîtrise
sur l'implémentation d'un parcours en longueur en itératif d'un graphe.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Ne pas hésiter à compléter la version à trous !
L'implémentation à préférer pour un graphe sur lequel on veut appliquer un parcours en profondeur est la liste d'adjacence.
En effet, les voisins de chaque sommet sont systématiquement visités : il y a une itération sur les voisins du sommet.
On note $n$ le nombre de sommets du graphe et $a$ le nombre d'arêtes (ou d'arcs dans le cas orienté).
On suppose que le graphe est implémenté comme dictionnaire d'adjacence.
Il est possible d'écrire un parcours en profondeur de complexité en temps proportionnel à $n+a$, c'est-à-dire en $O(n+a)$.
La complexité en mémoire de cet algorithme est aussi en $O(n+a)$.
Parcours en largeur
Exemple introductif
Revenons au labyrinthe de l'exemple introductif sur les parcours.

Plutôt que de suivre un chemin le plus loin possible pour revenir sur ses pas une fois un "cas-de-sac" atteint, nous allons plus "prudemment" parcourir le labyrinthe. L'idée est de visiter d'abord tout ce qui est très proche, puis tout ce qui est un peu plus loin, puis tout ce qui est un peu plus éloigné, ... en gagnant en confiance ainsi, nous atteindrons même les lieux les plus reculés. Plus précisément :
Un parcours en largeur d'un graphe revient à parcourir un graphe en explorant d'abord un sommet, puis ses sommets voisins, puis les voisins non encore explorés de ces voisins, et ainsi de suite jusqu'à ce que l'on ne découvre plus aucun sommet non encore exploré.
Quelle différence entre les deux parcours en profondeur et en largeur ?
En cas de "cul-de-sac", on repart de l'intersection pouvant nous apporter une information :
-
intersection intéressante la plus récente dans le cas du parcours en profondeur,
-
intersection intéressante la plus ancienne dans le cas du parcours en largeur.
On peut visualiser comment fonctionne ce parcours en largeur en l'appliquant sur le graphe modélisant le labyrinthe :
Voici la succession des sommets obtenus en parcourant suivant cette méthode le graphe en partant du sommet $A$ :
-
Suivre l'arête menant à $B$ :
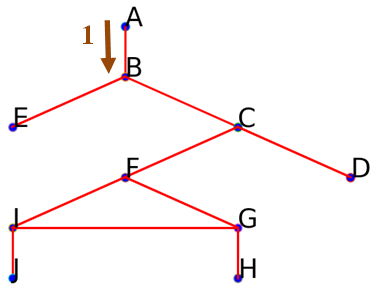 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B']. -
On a fini de visiter les voisins direct de $A$ (ici un seul).
On cherche maintenant les voisins de second niveau de $A$, ceux voisins de $B$.
Il y a deux sommets voisins de $B$.
Suivre l'arête menant à $E$ (on pourrait aussi aller vers $C$):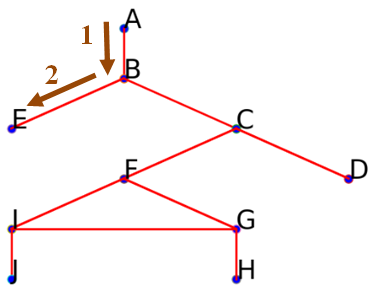 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E']. -
Sans chercher à savoir si l'on peut aller plus loin que $E$, visiter l'autre sommet voisin de $B$ possible : le sommet $C$.
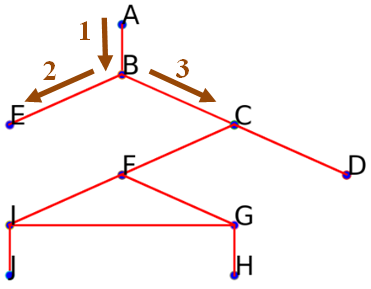 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C']. -
Comme il ne reste plus de voisins de $B$ non visités, on poursuis le parcours en partant désormais des voisins trouvés de $B$, c'est-à-dire de $E$ et de $C$. En d'autres termes, on cherche maintenant les voisins de troisième niveau de $A$
Comme $E$ est le sommet le plus anciennement trouvé, on cherche s'il existe de nouveaux sommets accessibles depuis $E$.
Comme il n'y en a pas, on poursuit avec le second sommet successeur de $B$ trouvé : $C$. $C$ permet d'accéder à deux nouveaux sommets $F$ et $D$. On suppose que $F$ est le premier sommet visité, on a donc :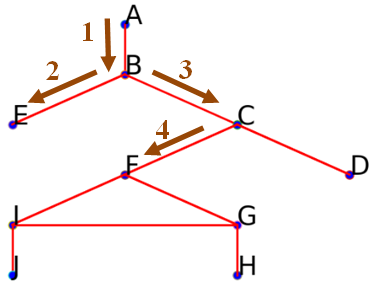 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F']. -
Sans chercher à savoir si l'on peut aller plus loin que $F$, visiter l'autre sommet voisin de $C$ possible : le sommet $D$.
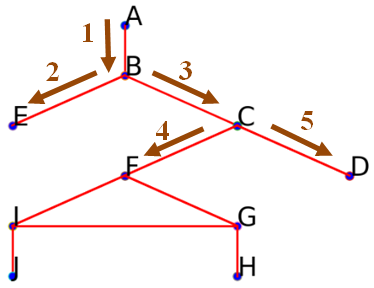 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F', 'D']. -
Comme il ne reste plus de voisins de $C$ non visités, on poursuis le parcours en partant désormais des voisins trouvés de $C$, c'est-à-dire de $F$ et de $D$. En d'autres termes, on cherche maintenant les voisins de quatrième niveau de $A$
Comme $F$ est le sommet le plus anciennement trouvé, on cherche s'il existe de nouveaux sommets accessibles depuis $F$.
$F$ permet d'accéder à deux nouveaux sommets $I$ et $G$. On suppose que $I$ est le premier sommet visité, on a donc :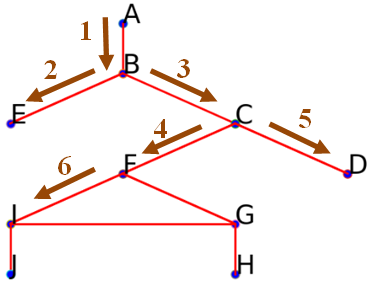 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F', 'D', 'I']. -
Sans chercher à savoir si l'on peut aller plus loin que $I$, visiter l'autre sommet voisin de $F$ possible : le sommet $G$.
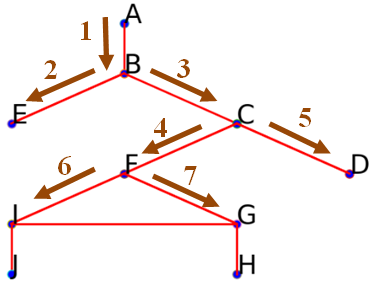 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F', 'D', 'I', 'G']. -
Comme on a fini avec les voisins de $F$, on cherche maintenant les voisins du sommet $D$ trouvé au même niveau que $F$.
Comme $D$ ne permet pas d'accéder à de nouveau sommet, on a fini de visiter les voisins des voisins de $C$. On cherche maintenant les voisins de cinquième niveau de $A$, ceux donc de $I$ et de $G$.
Comme $I$ a été visité le plus anciennement, on commence par étudié ses nouveaux voisins.
$I$ a trois voisins : $F$, $G$ et $J$. $J$ est le seul sommet non encore découvert.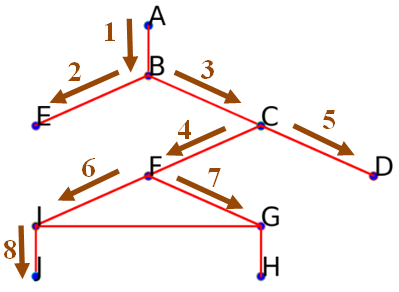 On obtient aussi le début parcours suivant :
On obtient aussi le début parcours suivant : ['A', 'B', 'E', 'C', 'F', 'D', 'I', 'G', 'J']. -
Sans chercher à savoir si l'on peut aller plus loin que $J$, visiter les voisins de l'autre sommet de même niveau que $I$ : $G$. $G$ a trois voisins : $F$, $I$ et $H$. $H$ est le seul sommet non encore découvert.
 On obtient aussi le parcours suivant :
On obtient aussi le parcours suivant : ['A', 'B', 'E', 'C', 'F', 'D', 'I', 'G', 'J', 'H']. -
Maintenant que l'on a terminé l'exploration du cinquième niveau (les sommets pour lesquels il faut au minimum passer par 4 sommets intermédiaires pour y accéder en partant du sommet initial $A$, cherchons s'il y a un sixième niveau.
Comme il n'existe pas de nouveau sommet à partir des sommets $J$ et $H$ du cinquième niveau, il n'y a pas de sixième niveau : l'exploration du graphe est terminée.
On obtient aussi aboutit au parcours suivant :['A', 'B', 'E', 'C', 'F', 'D', 'I', 'G', 'J', 'H'].
Pour un même graphe, les parcours en largeur et en profondeur conduisent à des parcours différents. Nous avions trouvé :
-
pour le parcours en profondeur le parcours suivant :
['A', 'B', 'E', 'C', 'F', 'I', 'J', 'G', 'H', 'D']. -
pour le parcours en largeur le parcours suivant :
['A', 'B', 'E', 'C', 'F', 'D', 'I', 'G', 'J', 'H'].
Vision naïve
Le parcours en largeur correspond à la stratégie de parcours de graphe suivante :
Si $v$ est un sommet voisin découvert d'un sommet $u$, on visite d'abord les voisins de $u$ avant de
visiter les autres voisins de $v$.
Lors de l'exploration, on cherche à toujours élargir la connaissance des sommets sans s'éloigner trop du
sommet de départ.
Chaque étape revient à partir des sommets se trouvant à une certaine distance du sommet initiale et à
chercher tous les sommets, non
encore visités, qui se trouvent à une distance augmentée de 1.
À chaque étape, on repart donc des sommets découverts à l'étape précédente, en commençant par le sommet le
plus ancien.
On retrouve bien le principe premier lieu rajouté, premier lieu retiré (car étudié) : c'est le principe d'une file.
L'implémentation d'un parcours en largeur se fait à l'aide d'une file.
Pour se souvenir de ce qui a déjà été exploré du reste, il est important de "marquer" tout endroit exploré afin de ne pas les visiter à nouveau. En pratique, dans un labyrinthe, si on a la chance d'avoir une craie, on peut écrire une marque ou colorier en partie un endroit.
Cette exploration pour tout découvrir du lieu peut s'écrire sous forme d'algorithme en langage naturel :
1. Partir du lieu le plus anciennement découvert (le plus ancien de la file d'attente). 2. Puis étudier tous les lieux voisins de cet endroit ; trois possibilités : cas 1 : si le lieu voisin a déjà été exploré (car marqué), on l'ignore, cas 2 : si le lieu voisin n'a pas encore été visité : on le rajoute à la liste d'attente et on recommence le 2. cas 3 : lorsque tous les voisins ont été visités : cet endroit n'a plus d'intérêt : on l'enlève de la liste d'attente. On recommence le 1. 3. On continue ainsi tant qu'il reste des lieux à étudier dans la file d'attente.
Quatre animations ci-dessous représentent 4 parcours différents sur le même graphe à partir du sommet 'A'.
-
Repérer le parcours qui correspond bien à un parcours en largeur du graphe à partir du sommet
'A'. -
Expliquer pourquoi les autres parcours ne sont pas un parcours en largeur du graphe à partir du sommet
'A'.
Parcours 1 :

Parcours 2 :

Parcours 3 :
Parcours 4 :

Version itérative
Nous avons déjà vu ci-dessus que "naturellement" l'implémentation d'un algorithme de parcours en largeur se fait à l'aide d'une file.
Dans cette file sera stocké temporairement l'ensemble des sommets non encore "étudiés", c'est-à-dire dont il reste à visiter les sommets voisins.
Voici en langage naturel, une fonction donnant un parcours en largeur en itératif :
fonction parcours_largeur(Graphe G, sommet s)
Créer la liste visites des sommets déjà visités, liste réduite pour l'instant au sommet s
Créer reste_a_voir une file vide
Ajouter les voisins du sommet s à la file reste_a_voir (=enfiler)
Tant que la file reste_a_voir n'est pas vide faire :
défiler la tête de la file reste_a_voir et la stocker dans une variable u
si u ne fait pas partie de la liste des sommets déjà visités faire :
rajouter u à la liste visites des sommets déjà visités
Pour tout sommet voisin v du sommet u faire :
si v ne fait pas partie de la liste des sommets déjà visités faire :
Ajouter le sommet v à la file reste_a_voir
renvoyer la liste visites des sommets visités
Comparer la fonction parcours_profondeur_iteratif en langage naturel avec
la fonction parcours_largeur ci-dessus.
Quelle différence remarquez-vous ?
Comme vu lors de la première implémentation du parcours en profondeur itératif,
on peut écrire l'algorithme de parcours en largeur en utilisant un graphe G défini par un dictionnaire
donnant la liste d'adjacence en partant d'un sommet s comme vu dans l'exercice suivant :
-
Reprendre le programme proposé à l'exercice implémentant d'une seconde manière le parcours en profondeur itératif et le modifier pour obtenir une implémentation d'un parcours en largeur.
-
Voici de nouveau une implémentation du graphe introductif du chapitre sur les graphes que l'on pouvait construire un graphe à partir d'un dictionnaire :
graphe = {} # création d'un dictionnaire vide graphe["A"] = ["B", "C", "E", "F", "H"] # liens de A vers les sommets listés graphe["B"] = ["A", "D", "H"] graphe["C"] = ["A", "F", "G", "H"] graphe["D"] = ["B", "H"] graphe["E"] = ["A", "H"] graphe["F"] = ["A", "C"] graphe["G"] = ["C", "H"] graphe["H"] = ["A", "B", "C", "D", "E", "G"]Tester la fonction
parcourir_largeuravec ce graphe. -
Décrire le parcours en largeur obtenu en partant du sommet "D".
-
Vérifier ce parcours grâce à la représentation ci-dessous de ce graphe.
-
où grâce à ce gif :
Vérifier si le programme fonctionne encore si un sommet n'est plus une clé du dictionnaire
graphe, par exemple avec
ce graphe orienté, qui correspond à celui précédent où "H" devient une impasse :
graphe = {}
graphe["A"] = ["B", "C", "E", "F", "H"]
graphe["B"] = ["A", "D", "H"]
graphe["C"] = ["A", "F", "G", "H"]
graphe["D"] = ["B", "H"]
graphe["E"] = ["A", "H"]
graphe["F"] = ["A", "C"]
graphe["G"] = ["C", "H"]
Modifier la fonction parcourir_largeur de sorte qu'elle fonctionne encore avec des graphes orientés.
Comme pour le parcours en longueur, il est intéressant pour ces raisons de coût en temps de remplacer
le test sur l'appartenance
à une liste visites par un test sur un marquage géré par dictionnaire
En s'inspirant de vos travaux effectués précédemment, modifier la fonction parcourir_largeur
obtenue dans l'exercice précédent
en utilisant un dictionnaire qui associe à chaque sommet une valeur 'inconnu' ou 'visite'.
Vous pourrez tester votre programme par exemple avec ce graphe orienté :  dont voici ci-dessous un dictionnaire le définissant le graphe :
dont voici ci-dessous un dictionnaire le définissant le graphe :
graphe_or = {'A': ['B', 'G'],
'B': ['C', 'E'],
'D': ['F', 'G'],
'E': ['A', 'D', 'H'],
'F': ['B', 'C'],
'H': ['F']
}
Voici un exercice à faire en autonomie pour tester votre maîtrise sur
le parcours (en largeur) de graphe à partir d'un problème
concret de transmission de rumeur.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
La version à trous est celle à savoir réaliser.
Comme vu pour le parcours en longueur, il est possible d'utiliser le module networkx pour implémenter
des graphes.
Dans cet exercice, vous pouvez vous aider du programme déjà obtenu à l'exercice
sur le parcours en profondeur en itératif
en utilisant la bibliothèque networkx :
-
vous prendrez une liste Python en guise de file en considérant que la tête de la file correspond au premier élément de la liste.
-
Le graphe sera supposé être un objet de la classe
Graph()de la bibliothèqueNetworkx; ceci permettra d'utiliser les méthodes de cette bibliothèque comme par exemple :-
graphe.neighbors(v)qui permet d'obtenir les voisins d'un sommetvdu graphegraphe, -
vous pourrez transtyper en liste l'itérable des voisins d'un sommet donné grâce à
list.
-
-
Écrire en langage Python une fonction
parcours_largeurqui correspond à la fonction vue ci-dessus en langage naturel.-
Penser à utiliser
liste[0]pour obtenir le premier élément de la listeliste. -
Penser à utiliser la méthode
poppour supprimer un élément d'une liste dont la position est connue tout en renvoyant l'élément supprimé.
-
-
Tester cet algorithme de parcours en profondeur en prenant le graphe sur les pays d'Amérique du Sud.
-
En vous aidant de la carte de l'Amerique du Sud ci-dessous, vérifier que la liste renvoyée correspond bien à un parcours en largeur.

L'algorithme de parcours en profondeur nécessite une pile ; l'algorithme de parcours en largeur nécessite une file. Pour les implémenter nous avons utiliser dans des listes.
Pour supprimer des éléments de cette liste (pour dépiler et
pour défiler), la méthode pop a été utilisée.
Cependant la complexité de cette méthode dans le cas où on défile est d'ordre linéaire. En effet, on supprime le premier élément de la liste et on doit décaler chacun des autres éléments.
Il existe d'autres structures de données en Python plus adaptée que les listes pour implémenter une file (ou une pile) :
-
soit créer directement ce type de structure en programmation objet comme vu lors des chapitres introduisant ces structures,
-
soit utiliser des modules spécifiques. Le module
collectionspermet d'introduire l'objetdeque. L'exercice suivant permet de découvrir ce module.Pour plus d'informations, vous pouvez la documentation officielle de cet objet.
-
Utiliser l'objet
dequedu modulecollectionsafin d'implémentation la file du parcours en profondeur.
Utiliser la méthodepopleft()sur cet objet afin de défiler la tête de la file.
La méthodeappendest une méthode existant aussi pour ce type d'objet et fonctionne comme pour les listes.Essayer d'utiliser aussi un dictionnaire pour marquer les sommets visités et faire en sorte que le script soit fonctionnel aussi pour des graphes orientés.
-
En utilisant la documentation officielle, comparer le coût en temps de
liste.pop(0)et dedeque.popleft().
Plutôt que d'utiliser une bibliothèque comme deque ou une classe file, on va supprimer l'utilisation
coûteuse en temps de reste_a_voir.pop(0) en balayant la liste implémentant la file judicieusement.
Cette file implémentera aussi la liste des sommets parcourus.
On va dans cet exercice modifier le dictionnaire de marquage : plutôt que d'associer à un sommet visité la chaîne de caractères "visite", il suffit de lui associé le booléen True.
Dernière modification, quitte à l'éloigner de celui du parcours en profondeur, on "marque" un sommet comme visité au moment de son enfilement et non plus au moment du défilement comme précédemment.
On suppose dans cet exercice que tout sommet apparaît comme clé du dictionnaire implémentant le graphe.
-
Compléter le script suivant de sorte de gérer le marquage par
Trueet de marquer un sommet au moment de l'enfilement :def parcourir_largeur(G, s): connus = {} for v in G: connus[v] = ... visites = [s] # liste des sommets progressivement visités file = [s] # file des sommets en attente ou en cours de visite pour la tête connus[...] = True while ...: tete = file.pop(0) # tête de la file for voisin in ...: if ...: connus[voisin] = ... visites.append(...) ... return visites -
Au lieu de supprimer l'élément de tête d'une liste servant de tête de file, on sert d'un indice
i, indiquant la position de la tête de la file dans la liste, que l'on augmente à chaque "défilement" Compléter la fonction suivante afin d'obtenir un parcours en largeur sans utiliser....pop(0):def parcourir_largeur(G, s): connus = {...} # dictionnaire créer par compréhension visites = [s] # file des sommets progressivement visités (sert de file aussi !) connus[s] = ... i = ... # indice de la tête de la file while i ... : # condition pour qu'il y ait encore au moins un sommet à "défiler" tete = ... # tête de la file for voisin in ...: if ...: connus[voisin] = ... ... ... return visites -
Comme il y a un seul "défilement" à chaque itération du
whileprécédent, lewhilepeut être remplacé par une bouclefor.
Proposer une fonctionparcours_largeurprenant en paramètre un graphegraphe(implémenté comme dictionnaire d'adjacence) et un sommetS, qui utilise deux bouclesforimbriquées et qui renvoie la liste des sommets du graphe obtenu lors d'un parcours en largeur en partant deS.
Pour des raisons pédagogiques, nous avons choisi d'insister sur un parcours en largeur qui ne diffère du parcours en longueur qu'au niveau de la structure stockant les sommets en attente : pile ou file.
Comme dans l'exercice précédent et aussi chez plusieurs auteurs, il peut aussi y avoir une différence quant au moment de marquer le sommet :
-
Lors d'un parcours en profondeur, on marque les sommets au moment de leur dépilement.
-
Lors du parcours en largeur précédent, on marque les sommets au moment de leur enfilement (pour éviter les doublons).
Vous connaissez désormais de type de parcours de graphe : celui en profondeur et celui en largeur.
Dans quels cas préférez l'un ou l'autre ?
-
Pour détecter des cycles ou rechercher des composantes connexes ou pour explorer profondément (comme un labyrinthe), le parcours en profondeur est préférable.
En terme de mémoire nécessaire, le parcours en profondeur nécessite une pile, dont la taille maximale est proportionnelle à la profondeur maximale, taille qui est souvent inférieure à la taille maximale de la file nécessaire pour un parcours en largeur car cette taille est proportionnelle au nombre maximum de voisins.
-
Pour trouver un chemin le plus court ou pour étudier des problème de propagation ou pour rechercher dans un voisinage d'un sommet, le parcours en largeur est préférable.
On note $n$ le nombre de sommets du graphe et $a$ le nombre d'arêtes (ou d'arcs dans le cas orienté).
On suppose que le graphe est implémenté comme dictionnaire d'adjacence.
Il est possible d'écrire un parcours en largeur de complexité en temps proportionnel à $n+a$, c'est-à-dire en $O(n+a)$.
La complexité en mémoire de cet algorithme est aussi en $O(n+a)$.
-
Un parcours en profondeur consiste à avancer dans le graphe tant que cela est possible, c'est-à-dire en visitant un voisin non encore marqué comme visité.
-
Un parcours en profondeur utilise une pile pour stocker les éléments à visiter :
-
soit explicitement dans un parcours itératif,
-
soit implicitement dans un parcours récursif (au travers de la pile de récursion).
-
-
Voici une manière d'écrire un parcours en profondeur en récursif dans un graphe
grapheen partant du sommetdepartet en utilisant un dictionnaire de marquage de visite :
(on suppose ici que tous les sommets apparaissent comme clé du dictionnaire implémentant le graphe)marques = {sommet: False for sommet in graphe} def parcours_longueur_recursif(graphe: dict, depart, marques: dict) -> None: marques[depart] = True print(depart) for voisin in graphe[depart]: if not marques[voisin]: parcours_longueur_recursif(graphe, voisin, marques) -
Voici une manière d'écrire un parcours en profondeur en itératif dans un graphe
grapheen partant du sommetdepartet en utilisant un dictionnaire de marquage de visite :
(on suppose ici que tous les sommets apparaissent comme clé du dictionnaire implémentant le graphe)def parcours_longueur_iteratif(graphe: dict, depart) -> None: marques = {sommet: False for sommet in graphe} marques[depart] = True visites = [depart] a_visiter = graphe[depart] # liste servant de pile de stockage des sommets à visiter while a_visiter != []: visite = a_visiter.pop() # dépilement du sommet marques[visite] = True visites.append(visite) for voisin in graphe[visite]: if not marques[voisin]: a_visiter.append(voisin) return visites -
Le parcours en largeur consiste à parcourir un graphe par éloignement progressif d'un sommet de départ, c'est-à-dire à visiter tous les voisins directs, puis les voisins de ces voisins directs, etc.
-
Un parcours en largeur utilise une file pour stocker les éléments à visiter.
-
Voici une manière d'écrire un parcours en largeur (forcément en itératif) dans un graphe
grapheen partant du sommetdepartet en utilisant un dictionnaire de marquage de visite :
(on suppose ici que tous les sommets apparaissent comme clé du dictionnaire implémentant le graphe)def parcours_largeur(graphe: dict, depart) -> None: marques = {sommet: False for sommet in graphe} marques[depart] = True visites = [depart] a_visiter = graphe[depart] # liste servant de file de stockage des sommets à visiter while a_visiter != []: visite = a_visiter.pop(0) # défilement de la tête marques[visite] = True visites.append(visite) for voisin in graphe[visite]: if not marques[voisin]: a_visiter.append(voisin) return visites
Détection de cycles
Démarche
Vous avez vu dans les cours la notion d'arbres et de graphes et vous avez vu des algorithmes assez proches sur ces notions. Comme un arbre est un graphe n'ayant pas de cycle, il est intéressant d'avoir un algorithme qui permet de détecter la présence ou non de cycles dans un graphe.
Rappel :
Un cycle est une chaîne fermée dont les arêtes sont distinctes.
Si besoin, vous pourrez revoir les définitions sur les graphes accessibles ici.
On peut identifier la présence d'un cycle en retombant lors d'un parcours sur un sommet déjà visité.
Le parcours en profondeur permet de détecter la présence de cycles dans un graphe.
Comme nous avions vu que l'on pouvait écrire l'algorithme de parcours en profondeur en récursif et en itératif, il est possible d'écrire un algorithme de recherche de cycles à la fois en récursif et en itératif.
Version itérative de la recherche de cycle :
L'idée est de reprendre une version itérative du parcours en profondeur comme par exemple la version déjà obtenue l'exercice accessible ici rappelée ci-dessous :
def parcourir_profondeur(G, s):
decouverte = {}
for v in G:
decouverte[v] = "inconnu"
for w in G[v]: # Rajout des sommets non présents comme clé
if w not in G:
decouverte[w] = "inconnu"
visites = [s]
reste_a_voir = G[s]
decouverte[s] = "visite"
while len(reste_a_voir)>0 :
u = reste_a_voir.pop(-1)
if decouverte[u] == "inconnu":
decouverte[u] = "visite"
visites.append(u)
if u in G.keys(): # cas où le sommet est présent comme clé
for v in G[u]:
if decouverte[v] == "inconnu":
reste_a_voir.append(v)
return visites Le script précédent convient uniquement à un graphe implémenté par une dictionnaire où chaque sommet apparaît comme clé.
Avec ce script, une obtient un parcours en profondeur différent de celui obtenu par récursivité.
-
Écrire une fonction
existe_cycle_iterqui prend deux paramètres :-
Gun graphe du type dictionnaire -
sun sommet de ce grapheG.
et qui renvoie un booléen suivant que le graphe
Gpossède ou non un cycle lors d'un parcours en profondeur partant du sommets. -
-
Tester cette fonction avec chacun des graphes de type dictionnaire donnés par les codes suivants :
graphe1 = {} graphe1["A"] = ["B"] graphe1["B"] = ["D", "H"] graphe1["C"] = ["A", "F", "G"] graphe1["D"] = ["E"] graphe1["E"] = ["A"] graphe1["G"] = ["H", "C"] graphe1["H"] = ["G"] graphe2 = {} graphe2["A"] = ["B", "C"] graphe2["B"] = ["D", "E"] graphe2["C"] = ["G", "H"] graphe2["E"] = ["F"]
On considère désormais le graphe orienté de type dictionnaire donné par le code suivant :
graphe3 = {}
graphe3["A"] = ["D", "E"]
graphe3["B"] = ["A", "C"]
graphe3["C"] = ["F", "G"]
graphe3["F"] = ["C", "G"]
graphe3["G"] = ["C", "F"]
graphe3["D"] = [] # pour que chaque sommet du graphe soit une clé du dictionnaire
graphe3["E"] = [] Représenter à la main ce graphe orienté. Possède-t-il un cycle ?
Que renvoie existe_cycle_iter(graphe3, 'A') ?
Que renvoie existe_cycle_iter(graphe3, 'B') ?
Comment utiliser la fonction existe_cycle_iter afin de s'assurer de l'existence ou
non d'un cycle dans un graphe donné quelconque ?
Version récursive de la recherche de cycle :
Voici une version récursive du parcours en profondeur d'un graphe où celui-ci serait implémentée sous forme d'un dictionnaire :
def parcours_profondeur_recursif(graphe, sommet, visites):
visites.append(sommet)
if sommet in graphe.keys():
for voisin in graphe[sommet]:
if voisin not in visites:
visites = parcours_profondeur_recursif(graphe, voisin, visites)
return visites -
Modifier le fonction
parcours_profondeur_recursifci-dessus afin de créer une fonctionexiste_cyclequi :-
prend en paramètres un graphe de type dictionnaire, un sommet du graphe, une liste
visiteset un booléenbool;
ce booléenboolvaudraFalsesi aucun cycle n'est détecté etTruesinon. -
renvoie un tuple contenant une liste et un booléen.
-
-
Tester la fonction
existe_cycleen partant du sommet $A$ avec le graphe orienté donné ci-dessous :graphe1 = {} graphe1["A"] = ["B"] graphe1["B"] = ["D", "H"] graphe1["C"] = ["A", "F", "G"] graphe1["D"] = ["E"] graphe1["E"] = ["A"] graphe1["G"] = ["H", "C"] graphe1["H"] = ["G"] -
Tester la fonction
existe_cycleen partant du sommet $A$ avec le graphe orienté donné ci-dessous :graphe2 = {} graphe2["A"] = ["B", "C"] graphe2["B"] = ["D", "E"] graphe2["C"] = ["G", "H"] graphe2["E"] = ["F"]
Voici un exercice à faire en autonomie pour tester votre maîtrise
sur le parcours de graphe à partir d'un problème
concret de transmission circulaire de cadeaux.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
La version à trous est celle à savoir réaliser.
Chemin dans un graphe
Pour chercher un chemin entre un sommet de départ et un autre, il suffit de parcourir le graphe à partir du sommet de départ, en contrôlant à chaque étape si le sommet étudié correspond à celui recherché, tout en conservant la trace des arêtes (ou arcs) parcourues.
Le parcours en largeur d'un graphe permet de trouver un chemin entre deux sommets, si ce chemin existe.
Voici donc un moyen pour créer un algorithme de recherche de chemin entre deux sommets d'un graphe :
On peut créer un algorithme de recherche de chemin entre un sommet de départ et un d'arrivée en utilisant :
-
un parcours en largeur,
-
de contrôler à chaque étape si le sommet à traiter correspond à celui d'arrivée cherché,
-
de garder la trace des arêtes parcourues en utilisant un dictionnaire associant à chaque sommet un prédécesseur permettant de l'atteindre.
Pour rappel, un script parcours en largeur a été obtenu à cet exercice où
G est un graphe implémenté sou forme d'un dictionnaire d'adjacence.
Voici ci-dessous un script
def parcourir(G, depart, arrivee) :
"""
G est un graphe implémenté par un dictionnaire
depart est un sommet de ce graphe G, celui de départ
arrivee est un sommet de ce graphe G, celui d'arrivée
"""
predecesseur = {depart: None} # predecesseur est un dictionnaire associant à chaque sommet du graphe un sommet permettant de l\'atteindre directement
reste_a_voir = [depart]
while len(reste_a_voir)>0 :
u = reste_a_voir.pop(0)
if u == arrivee:
return True
if u in G: # ou ... in G.keys()
for v in G[u]:
if v not in predecesseur.keys():
predecesseur[v] = u
reste_a_voir.append(v)
return False -
Commenter chaque ligne de ce script.
-
À quel type de parcours correspond ce script ? Justifier.
-
Tester ce script en cherchant l'existence d'un chemin entre les sommets "C" et "E" pour chacun des graphes suivants :
graphe1 = {} graphe1["A"] = ["B"] graphe1["B"] = ["D", "H"] graphe1["C"] = ["A", "F", "G"] graphe1["D"] = ["E"] graphe1["G"] = ["H", "C"] graphe1["H"] = ["G"]puis :
graphe2 = {} graphe2["A"] = ["B", "C"] graphe2["B"] = ["D", "E"] graphe2["C"] = ["G", "H"] graphe2["E"] = ["F"]
Le script précédent ne renvoie pas le chemin possible reliant deux sommets dans le cas où un tel chemin existe.
Le but de ce exercice est de compléter le script précédent afin d'obtenir un tel chemin.
en utilisant le dictionnaire
predecesseur modifié lors de l'utilisation de la fonction parcourir de
l'exercice précédent.
-
Modifier la fonction
parcourirde l'exercice précédent pour qu'elle renvoie le booléen donnant l'existence d'un chemin mais aussi le dictionnairepredecesseurconstruit lors du parcours. -
Créer une fonction
rechercher_cheminqui :-
prend en paramètre un graphe (de type dictionnaire) (possiblement orienté) et deux sommets de celui-ci,
-
fait appel à la fonction
parcourirde l'exercice précédent pour savoir si un tel chemin existe et pour connaître le dictionnairepredecesseur, -
part du sommet d'arrivée et utilise le dictionnaire
predecesseurpour aboutir au départ. -
renvoie le chemin permettant de relier les deux sommets en cas d'existence sous forme d'une liste de sommets successifs.
-
renvoie une liste vide en cas d'absence de chemin possible.
Copier puis compléter le script suivant en vous servant des commentaires et du test proposé ci-dessus.
def rechercher_chemin(G, depart, arrivee): """ G est un graphe implémenté par un dictionnaire depart est un sommet de ce graphe G, celui de départ arrivee est un sommet de ce graphe G, celui d'arrivée renvoie une liste : vide en cas d'absence d'existence d'un chemin permettant de relier depart à arrivee donnant la succession des sommets à suivre pour relier depart à arrivee """ chemin = [] # stocke la liste des sommets permettant de relier depart à arrivee en partant de l'arrivée booleen, predecesseur = parcourir(G, depart, arrivee) # utilisation du parcours en largeur # predecesseur est un dictionnaire associant à un sommet son premier prédécesseur connu. if ...: # cas où un chemin entre depart et arrivee existe. sommet = arrivee chemin = [...] # on construit à rebours le chemin while ...: # on continue à remplir jusqu'à atteindre le sommet de départ sommet = predecesseur[...] # le nouveau sommet du chemin est "le" prédécesseur du précédent. chemin.append(...) chemin.reverse() # on réordonne du départ à l'arrivée le chemin obtenu s'il existe ou la liste vide sinon. return ... # tests : graphe1 = {} graphe1["A"] = ["B"] graphe1["B"] = ["D", "H"] graphe1["C"] = ["A", "F", "G"] graphe1["D"] = ["E"] graphe1["G"] = ["H", "C"] graphe1["H"] = ["G"] graphe2 = {} graphe2["A"] = ["B", "C"] graphe2["B"] = ["D", "E"] graphe2["C"] = ["G", "H"] graphe2["E"] = ["F"] def parcourir(G, depart, arrivee) : """ G est un graphe implémenté par un dictionnaire depart est un sommet de ce graphe G, celui de départ arrivee est un sommet de ce graphe G, celui d'arrivée """ predecesseur = {depart: None} reste_a_voir = [depart] while len(reste_a_voir) > 0: u = reste_a_voir.pop(0) if u == arrivee: return True, predecesseur # renvoi aussi du dictionnaire if u in G: for v in G[u]: if v not in predecesseur.keys(): predecesseur[v] = u reste_a_voir.append(v) return False, predecesseur # renvoi aussi du dictionnaire print(rechercher_chemin(graphe1, "C", "E")) print(rechercher_chemin(graphe2, "C", "E")) -
-
Tester ce script en cherchant l'existence d'un chemin entre les sommets "C" et "E" pour chacun des graphes suivants :
graphe1 = {} graphe1["A"] = ["B"] graphe1["B"] = ["D", "H"] graphe1["C"] = ["A", "F", "G"] graphe1["D"] = ["E"] graphe1["G"] = ["H", "C"] graphe1["H"] = ["G"]puis :
graphe2 = {} graphe2["A"] = ["B", "C"] graphe2["B"] = ["D", "E"] graphe2["C"] = ["G", "H"] graphe2["E"] = ["F"]représentant les graphes suivants :
 et
et
Compléter le script python suivant afin que la fonction
plus_court_chemin_largeur renvoie le plus
court chemin entre les sommets depart et arrivee
du graphe graphe (dictionnaire d'adjacence)
def plus_court_chemin_largeur(graphe, depart, arrivee):
visites = [...]
predecesseur = {depart: None}
for sommet in visites:
# Cas où on reconstruit le chemin trouvé à partir de l'arrivée
if ...:
chemin = []
while ...:
chemin.append(...)
sommet = predecesseur[...]
# Inversion de l'ordre de chemin par création de liste par compréhension
n = len(chemin)
return [...]
# sinon, on visite les voisins qui n'ont pas déjà été vus
if sommet in graphe:
for voisin in ...:
if ...:
predecesseur[...] = ...
visites.append(...)
L'algorithme obtenu précédemment, pour obtenir un chemin reliant deux sommets dans le cas où celui existe, n'est pas optimal en terme de coût.
Comme vu dans certains exercices du chapitre, il est préférable d'utiliser un objet deque du module collections
pour implémenter une file.
-
L'algorithme exhibé utilisant un parcours en largeur nécessite d'explorer tous les sommets. Il existe des algorithmes qui recherchent un chemin entre deux sommets en cherchant d'abord certains types de chemins en étudiant globalement les deux sommets avant d'élargir la recherche. L'algorithme A* est un exemple de tel algorithme.
-
Souvent, on ne se contente pas de trouver le nombre minimal de sommets entre deux sommets, mais souvent on cherche à savoir quel est le plus court chemin parmi tous ceux existant dans un graphe pondéré en prenant la valeur des poids.
Pour répondre à cette question, il existe plusieurs algorithmes possibles, en particulier celui de Dijkstra.
Ces algorithmes sont hors programme.
Exercices du baccalauréat
Exercices
Parcours
Voici ci-dessous la représentation d'un graphe non-orienté $G$ :
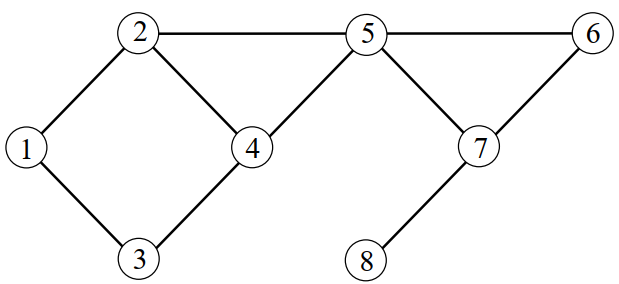
-
Est-ce que la liste $[5, 6, 7, 4, 3, 1, 8, 2]$ est un parcours de ce graphe $G$ ? Pourquoi ?
-
Est-ce que la liste $[5, 6, 3, 4, 7, 8, 1, 2]$ est un parcours de ce graphe $G$ ? Pourquoi ?
-
Proposer un parcours en profondeur possible de ce graphe en partant de la racine 5. Est-il unique ? Pourquoi ?
-
Est-ce que la liste $[5, 7, 8, 2, 1, 3, 4, 6]$ est un parcours en profondeur de ce graphe $G$ ? Pourquoi ?
-
Est-ce que la liste $[5, 7, 6, 8, 4, 2, 1, 3]$ est un parcours en profondeur de ce graphe $G$ ? Pourquoi ?
-
Proposer un parcours en largeur possible de ce graphe de racine 5. Est-il unique ? Pourquoi ?
-
Est-ce que la liste $[1, 2, 3, 4, 5, 6, 7, 8]$ est un parcours en largeur de ce graphe $G$ ? Pourquoi ?
-
Est-ce que la liste $[5, 6, 7, 2, 4, 8, 3, 1]$ est un parcours en largeur de ce graphe $G$ ? Pourquoi ?
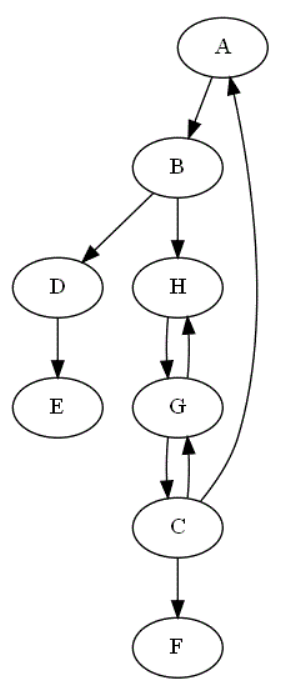
Voici un graphe orienté.
source : Marie-José Huguet de l'INSA de Toulouse
-
Suivre pas à pas l'algorithme de parcours en profondeur itératif avec trois couleurs travaillé dans cet exercice en partant du sommet $A$ pour appliquer l'effet progressif sur chacun des sommets de ce graphe.
À chaque étape, montrer aussi comment évolue la pile.
-
Déterminer le parcours en profondeur de ce graphe lorsque l'on part du sommet $A$.
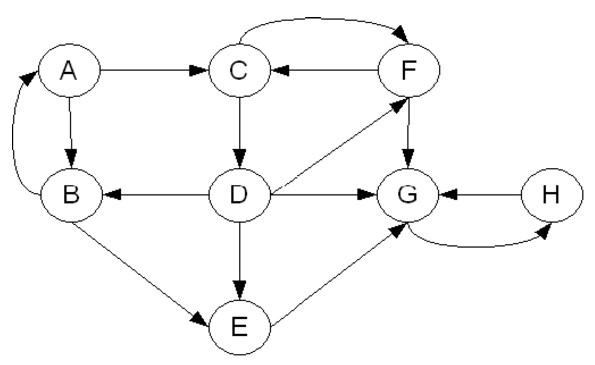
Voici un graphe orienté.

source : Marie-José Huguet de l'INSA de Toulouse
Pour rappel, voici une écriture possible en langage Python du parcours en largeur ; écriture obtenu lors de cet exercice.
def parcourir_largeur(G, s):
couleur = {}
for v in G:
couleur[v] = 'blanc'
for w in G[v]:
if w not in G:
couleur[w] = 'blanc'
predecesseur = {}
predecesseur[s] = None
couleur[s] = 'gris'
file = [s]
while len(file) > 0:
u = file[0]
succes = []
if u in G:
for v in G[u]:
if couleur[v] == 'blanc':
succes.append(v)
if len(succes) > 0:
v = succes[0]
couleur[v] = 'gris'
predecesseur[v] = u
file.append(v)
else :
file.pop(0)
couleur[u] = 'noir'
return predecesseur
-
Suivre pas à pas l'algorithme de parcours en largeur avec trois couleurs ci-dessus en partant du sommet $A$ pour appliquer l'effet progressif sur chacun des sommets de ce graphe.
À chaque étape, montrer aussi comment évolue la file.
-
Déterminer le parcours en largeur de ce graphe lorsque l'on part du sommet $A$.
Exercice qui reprend la plupart des notions vues dans ce chapitre.
Vous êtes Ariane, fille de Minos, roi de Cnossos en Crète, et vous désirez aider Thésée ce grand héros à trouver le Minotaure enfermé dans le Labyrinthe construit par l'ingénieux Dédale puis a pouvoir en ressortir une fois le monstre tué.
Vous aviez comme première idée de lui donner une longue pelote de laine, qu'il déviderait tout au long de sa progression initiale afin que votre héros puisse à l'issu du combat retrouver la sortie. Mais un fil est si fragile ... Le sentiment que le vie de Thésée ne tienne qu'à un fil vous est insupportable alors vous imaginez un autre stratagème.
Vous expliquez à Thésée comment parcourir complètement le labyrinthe pour l'explorer, découvrir le monstre et enfin pouvoir ressortir, mais si Thésée est un héros courageux et vaillant, il ne brille pas par son intelligence. Plus d'autre choix : vous l'accompagnerez et vous gérerez l'exploration complète du labyrinthe tandis que Thésée gérera le monstre.
-
Citez deux méthodes que vous connaissez pour explorer complètement le labyrinthe.
-
Voici ci-dessous le plan que Dédale a suivi pour la construction du labyrinthe : chaque salle s'est vue attribuée une lettre et les deux carrefours un numéro.
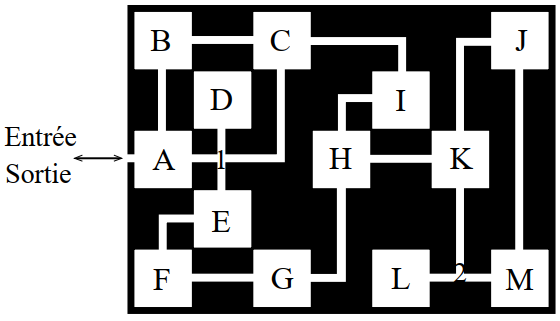 Source : Sylvie Borne
Source : Sylvie Borne
Créer le graphe représentant le labyrinthe en l'implémentant à l'aide d'un dictionnaire dont les entrées seront les lettres des salles et les numéros de carrefours.
Contrainte imposée : vous commencerez par les carrefours puis par les pièces en respectant l'ordre alphabétique.
-
Implémenter la méthode qui permet de progresser le plus prudemment dans ce labyrinthe sous forme d'une fonction qui prend en paramètre un graphe implémenté comme à la question précédente et en sortie renvoie le parcours obtenu.
Pour le parcours renvoyé, vous choisirez ce qui vous paraît le plus pertinent pour ressortir comme implémentation entre la liste des sommets visités ou un dictionnaire où à chaque salle ou numéro de carrefour est associé à la salle ou carrefour le précédent dans le parcours.
-
Vous avez trouvé le Minotaure dans la salle M. Thésée a été formidable : le monstre est tué ; désormais la jeunesse d'Athènes ne sera plus en partie dévorée par cette abomination. Il vous reste à sortir Thésée et vous.
Utilisez votre fonction précédente pour proposer un chemin qui vous ramènera à la salle A, seule issue possible de ce labyrinthe. Expliquez comment vous procédez.
-
Vous sortez avec Thésée du labyrinthe. Vous proposez à Thésée d'en faire votre demeure : nul ne viendrez vous y importuner. Cependant, Thésée trouve qu'il n'est pas simple pour lui de trouver rapidement un chemin lui permettant d'aller profondément dans le labyrinthe. Pour le convaincre, vous lui expliquez le parcours en profondeur et proposez de l'appliquer ensemble.
Implémenter le parcours en profondeur sous forme d'une fonction qui prend en paramètre un graphe implémenté comme à la première question et en sortie renvoie le parcours obtenu.
Pour le parcours renvoyé, vous choisirez ce qui vous paraît le plus pertinent pour ressortir comme implémentation entre la liste des sommets visités ou un dictionnaire où à chaque salle ou numéro de carrefour est associé à la salle ou carrefour le précédant dans le parcours.
-
Thésée vous demande de tester votre programme pour faire l'aller-retour entre les salles A et I.
-
Thésée trouve que le chemin obtenu avec le parcours en profondeur est parfois long, comme celui menant de "A" à "L" :
["A", "B", "C", "I", "H", "K", "J", "M", "2", "L"]; Thésée se lasse vite...Pouvez-vous proposer une fonction nommée
cheminqui prend en paramètre un graphe implémenté comme lors de la première question, deux sommets correspondant respectivement au départ et à l'arrivée, fonction qui renvoie le chemin à suivre pour aller directement du sommet de départ au sommet d'arrivée ?Réalisez une telle fonction car sinon Thésée risque d'abandonner votre projet.
Savoirs et savoirs-faire
-
savoir la notion de parcours sur un graphe,
-
savoir la notion de cycle sur un graphe,
-
savoir la notion de chemin sur un graphe,
-
savoir appliquer le parcours en profondeur sur un graphe donné,
-
savoir appliquer le parcours en largeur sur un graphe donné,
-
savoir écrire en langage Python un parcours en profondeur (itératif ou récursif),
-
savoir écrire en langage Python un parcours en largeur,
-
modéliser un labyrinthe par un graphe,
-
savoir utiliser les dictionnaires pour implémenter et étudier un graphe.
Sitographie
Voici quelques liens:

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International