La méthode diviser pour régner

Le principe "diviser pour régner" ("divide and conquer") est un principe militaire ancestrale. Cette stratégie était déjà mis en avant par Jules César "divide et impera", elle est reprise également dans les écrits politiques de Nicolas Machiavel ( article wikipédia sur Machiavel ).

Ce principe en informatique s'applique de préférence avec de la récursivité.

Diviser pour régner

La méthode de "Diviser pour régner" en algorithmique se décompose en trois étapes :

Diviser : on divise l'instance de départ en de plus petites.
Régner : on résout l'algorithme sur les "petites" instances précédentes.
On fusionne les résultats précédents pour obtenir le résultat final.

Un concours informatique est organisé. Il y a 100 candidats. Le travail de chaque candidat a été évalué et on a attribué une note à chacun.

Le règlement du concours impose de rendre les résultats dans l'ordre croissant des notes.

L'ordinateur qui devait trier les copies est en panne. (les cordonniers sont les plus mal chaussés...)

Il faut donc trier à la main.

Bob l'organisateur du concours a une idée ( si, si vraiment ) : Il va diviser le tas de copies. Il demande à son collègue Bobby de trier la moitié des copies pendant que lui triera l'autre moitié. Il procédera à la fusion par la suite.

Diviser : la tas de copies est divisé en deux.
Régner : chaque demi paquet est trié.
On finit par fusionner les deux paquets.

Encore plus malin, Bob fait appel à deux autres de ses connaissances : Bobus et Bobo. Ainsi le paquet sera divisé en quatre...

Le principe "diviser pour régner" permet d'écrire des algorithmes avec un complexité qui peut être plus faible que d'autres algorithmes pour un même problème (Théorème maître).

Tri fusion

L'algorithme de tri fusion est capable de trier un tableau d'objets munis d'une relation d'ordre. (entier, flottant,...)

Performance et complexité

Nous avons vu en première différents algorithmes de tri. (sélection, insertion). Ces algorithmes ont une complexité en temps quadratique, c'est-à-dire de l'ordre de $n^2$.

L'algorithme de tri fusion va nous permettre d'obtenir une complexité d'ordre $nlog_2(n)$.

Observer ces deux courbes pour comprendre le gain en temps.

Observer ce tableau pour comprendre le gain en temps.

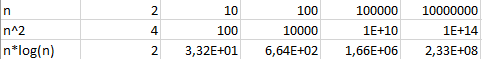
Dans le cas d'un tri de 10 000 000 d'éléments, combien peut-on faire de tris fusion pendant le temps nécessaire à un tri insertion ?

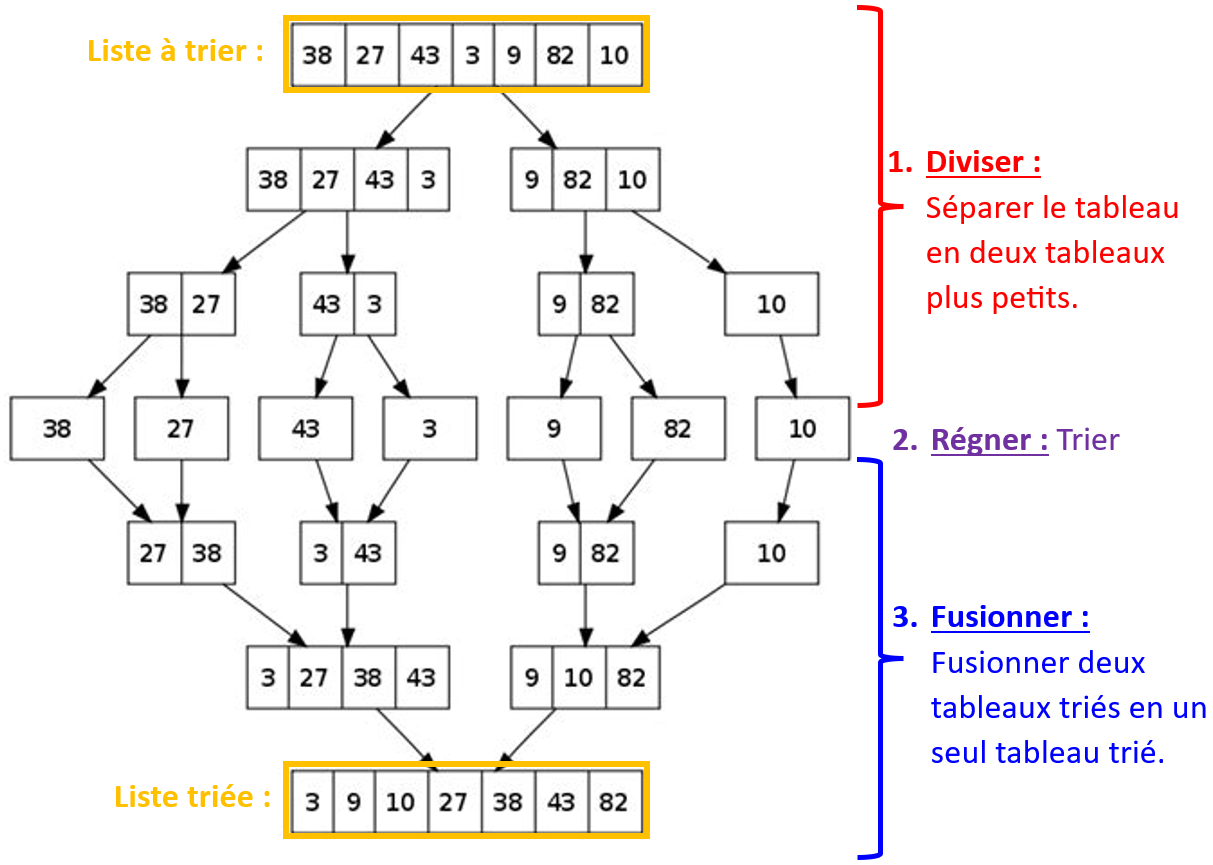
L'algorithme de tri fusion.

Algorithme de tri fusion et méthode diviser pour régner.

Diviser : on divise notre tableau en tableaux 2 fois plus petits.
Régner : on trie chacun des tableaux récursivement.
Fusionner : on fusionne les tableaux triés obtenus par récursivité.

Proposer une fonction separer en langage Python qui prend en paramètre une liste l et qui renvoie un tuple formé de deux listes ; la première contient la première moitié des termes et la seconde contient la deuxième moitié dans chacun des cas suivant :

Vous pouvez dans un premier temps écrire un script qui permet de découper une liste en deux parties équivalentes, puis de le transformer en fonction.

avec slice

Code de déblocage de la correction :
sans slice sans compréhension de liste

Code de déblocage de la correction :
sans slice en compréhension de liste

Code de déblocage de la correction :

Écrire une fonction fusionner(gauche, droite) qui prend en argument deux listes triées gauche et droite et qui renvoie une liste triée correspondant à la fusion de gauche et droite.

Cet exercice est difficile, ne vous découragez pas, il est essentiel au cours.

Écrire une fonction tri_fusion(l) qui prend en argument une liste l et qui renvoie la liste l triée avec la méthode de tri par fusion.

Vous devez utiliser les fonctions separer et fusionner créées lors deux exercices précédents.

S'aider de la propriété 2, en particulier en associant à chaque étape une fonction.

Quelques aides en vidéo pour les différentes fonctions :

Pour la fusion des listes :
Pour le tri fusion :
Tri fusion, trace Python tutor :

Rotation d'image

Inspiré du livre : NSI TLE GÉNÉRALE (SPÉCIALITÉ) - PRÉPABAC COURS & ENTRAÎNEMENT chez Hatier.

Dans tout cette partie, on utilisera le module PIL.

Image

Une image est un tableau de pixels.

Une image en 1024x720 se compose de 1024x720 pixels.

Chaque pixel a une couleur. La couleur est définie à partir de ses trois composantes : rouge, vert et bleu.

On définit un repère en prenant comme origine le coin en haut à gauche de l'image.

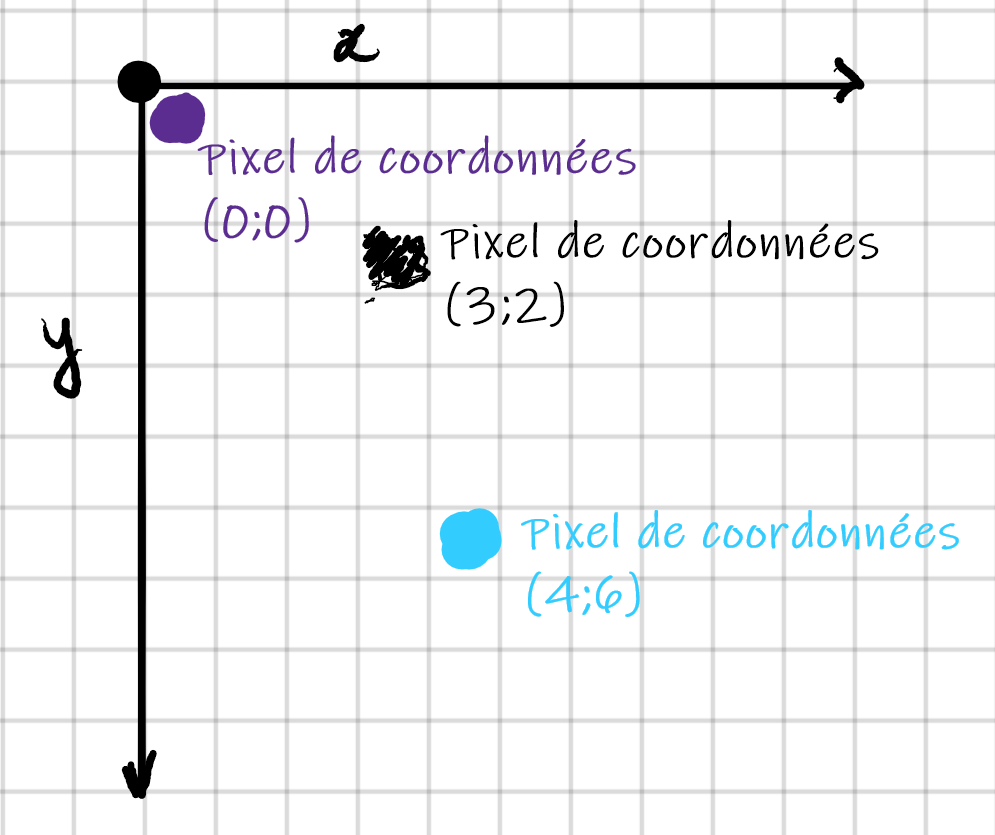
Voici une représentation d'une image :

La taille de cette image est : $7\times 6$

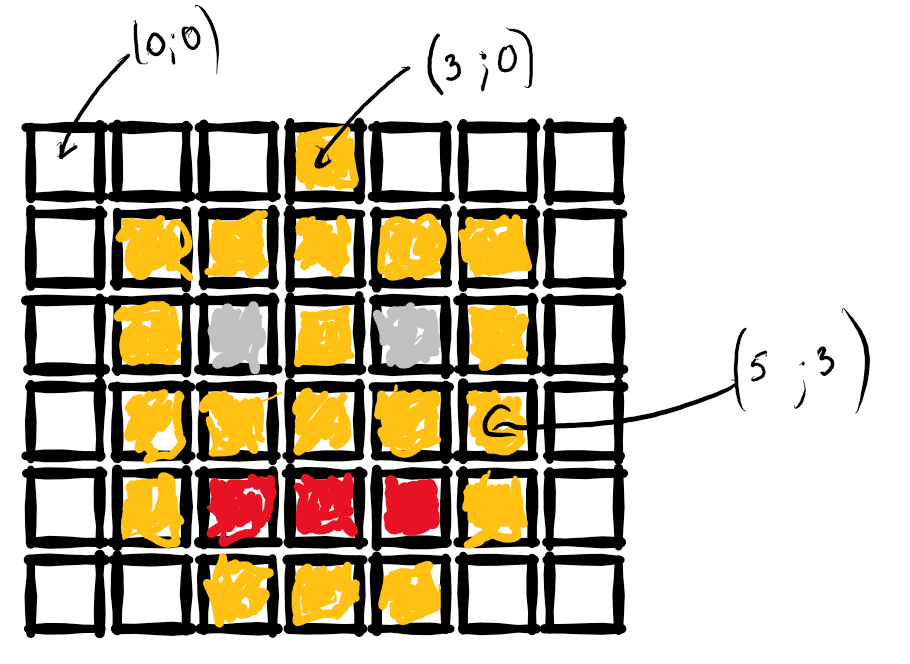
Vous avez peut-être vu en SNT que le module PIL permet de travailler en Python sur des images.
Pour cela, il suffit d'importer la classe Image.
Un pixel est alors repéré par ses coordonnées (x, y) et dont ses composantes rouge, vert et bleue sont notées (R, V, B).

Voici quelques méthodes de cette classe Image

Pour créer une nouvelle image (vide) de largeur L et de hauteur H, il suffit d'utiliser le constructeur new :

Nim = Image.new("RGB" , (L, H )) # Créer une nouvelle image nommée "Nim" de dimensions L et H

Pour créer un objet image nommé Nim à partir d'une image existante nommée image.format, il suffit d'utiliser la méthode open :

Nim = Image.open(chemin_acces/image.format) # charger une image en mémoire

Pour lire les informations (r, v, b) du pixel de coordonnées (x, y) de l’image nommée Nim, on utilise la méthode getpixel :

r, v, b = Nim.getpixel ((x, y ))

Pour récupérer les dimensions de l'image Nim, on utilise l'attribut size :

largeur, hauteur = Nim.size

Pour affecter les informations (r, v, b) au pixel de coordonnées (x, y) de l’image "Nim", on utilise la méthode putpixel:

Nim.putpixel((x, y), (r, v, b))

À l'aide la librairie PIL de Python, nous allons manipuler des images (plus d'informations sur le module PIL ici).

Nous allons travailler sur cette image :

la photo du prof

Télécharger ici

Tester et commenter le code ci-dessous :

from PIL import Image
im = Image.open("image.png")
largeur, hauteur = im.size
im.show()

Donner les dimensions de l'image.

Code de déblocage de la correction :
Donner la couleur du pixel de coordonnées (100 ; 100). (utiliser la methode getpixel())

Code de déblocage de la correction :
Remplacer la couleur des pixels se situant dans un carré de dimension 100 pixels au centre de la photo par la couleur en RGB (25, 153, 89). (utiliser la methode putpixel())

Code de déblocage de la correction :
Redimensioner l'image pour qu'elle soit deux fois plus petite.
Vous pouvez aller voir les fonctionnalités du module PIL.

Code de déblocage de la correction :

Rotation image, algorithme naïf.

Rotation d'un quart de tour.
Un pixel de coordonnées $(x ; y)$ dans une image de taille $n\times n$ a pour coordonnées avant rotation d'un quart de tour en sens horaire $(y ; n-1-x)$.

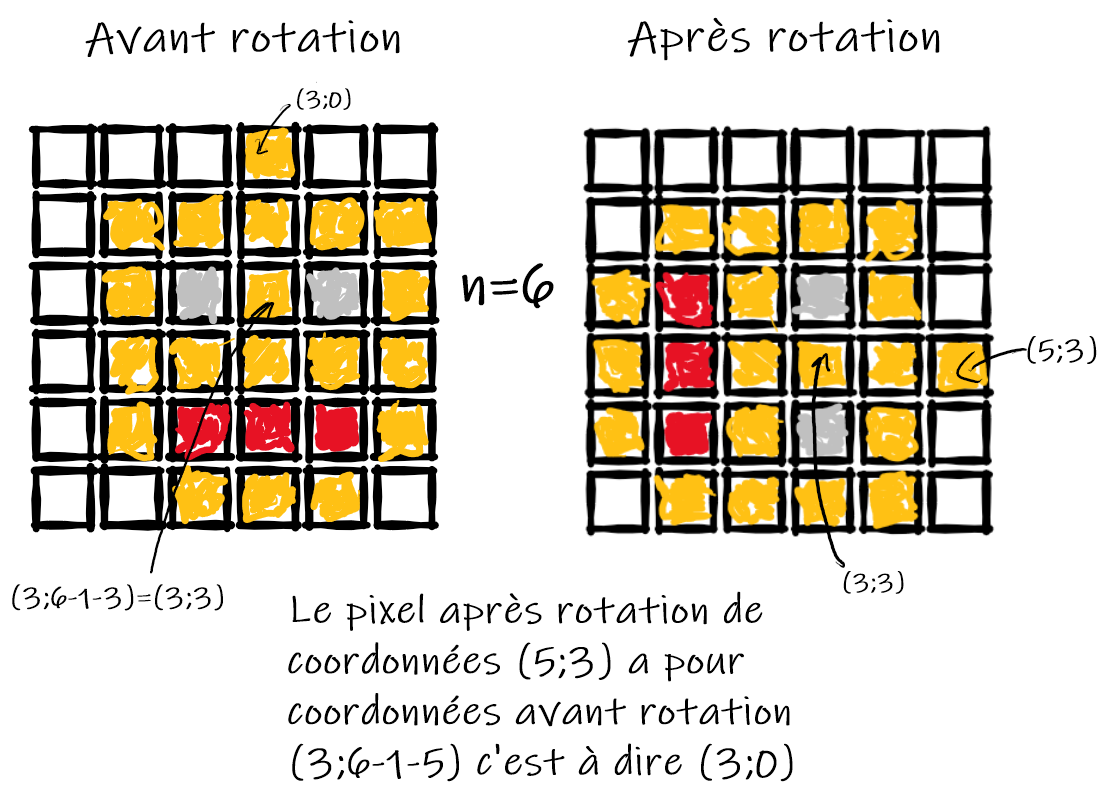
Écrire la fonction rotation(image,n) qui reçoit pour paramètres une chaîne de caractères correspondant au nom de l'image carrée et un entier $n$ correspondant à la taille de l'image et qui affiche l'image retournée de 90° dans le sens des aiguilles d'une montre.

On suppose ici que l'image en de format png.

Déterminer l'ordre de grandeur de la complexité de cet algorithme.

On divise, on règne sur les images !

Dans toutes cette partie, on se contentera de faire tourner une image carrée dont la taille est une puissance de 2.

Diviser pour régner

La méthode de "Diviser pour régner" en algorithmique se décompose en trois étapes :

Diviser : on découpe l'image en images de taille divisée par 2,
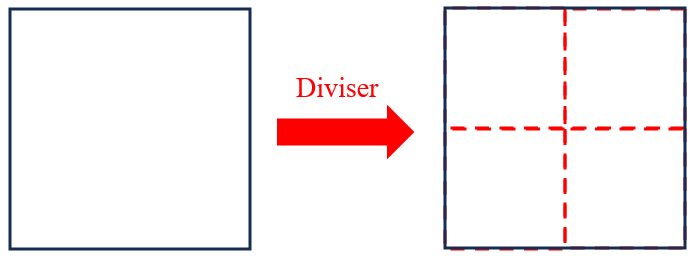
Régner : on effectue la rotation de chaque image de taille réduite,
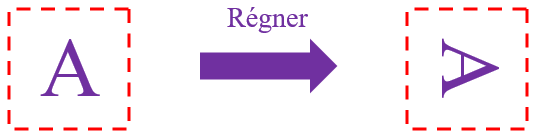
Fusionner : la fusion est réalisée en échangeant les cadrants lors des appels récursifs.

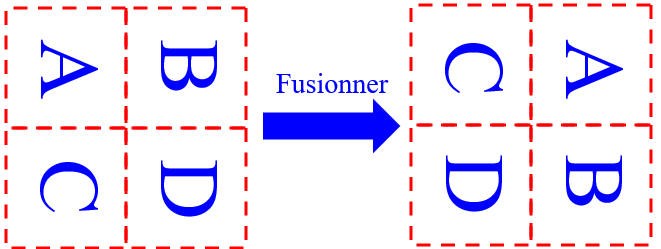
Écrire une fonction echangePixel(image, x1, y1, x2, y2) qui échange la valeur des pixels de coordonnées (x1, y1) et (x2, y2) dans l'image nommée image.

Écrire une fonction echangeCarre(image, x1, y1, x2, y2, n) qui échange des parties de l'image carrée de taille n dont les coordonnées de leur premier pixel est (x1, y1) et (x2, y2).

On utilisera la fonction echangePixel.

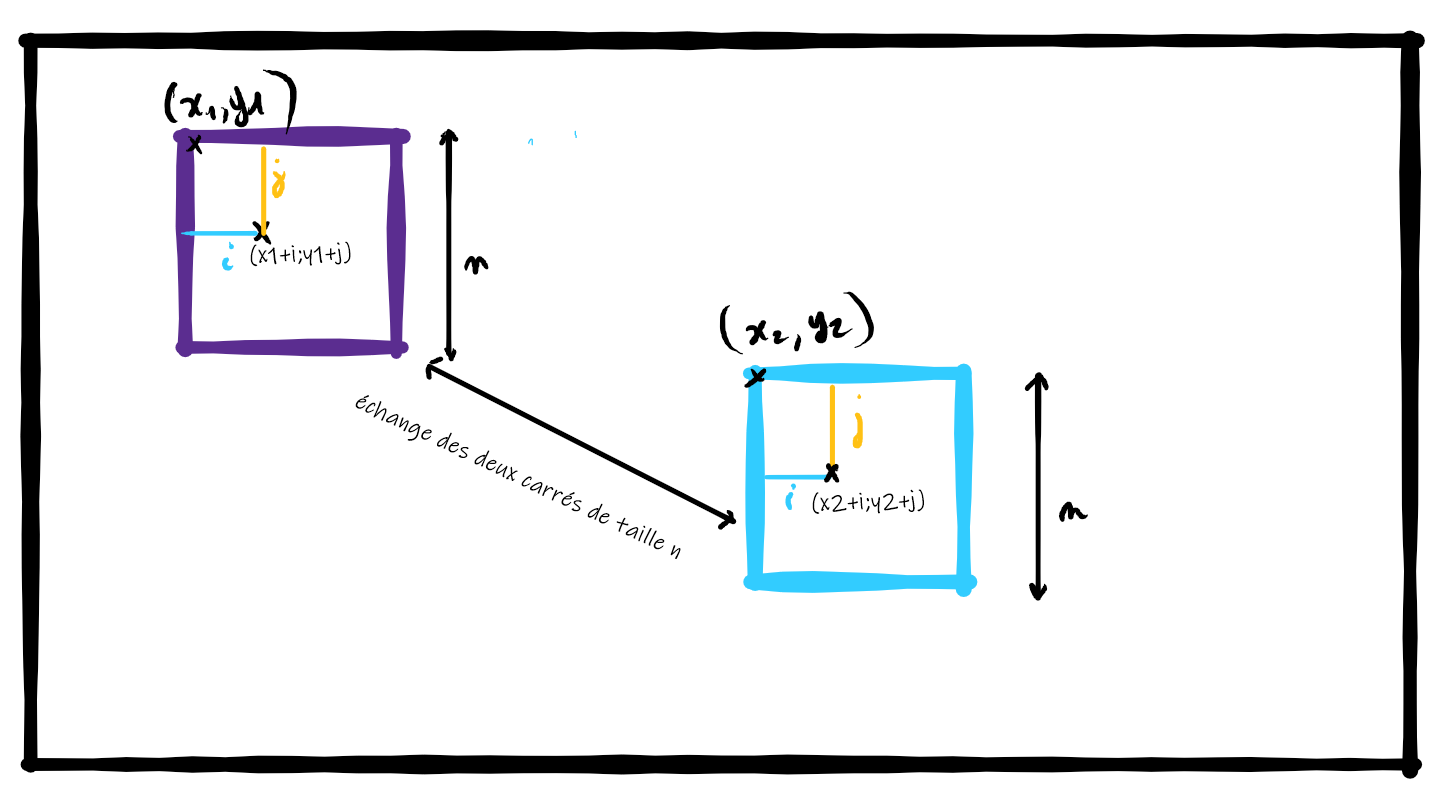
Vous disposez d'une fonction echange(Carré_a,Carré_b) qui permet d'échanger deux carrés dans une image.

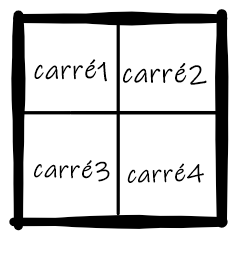
On notera une image carré découpée en quatre carrés de cette manière:

Quelle est la procédure qui permet de réaliser l'echange ci-dessous ?

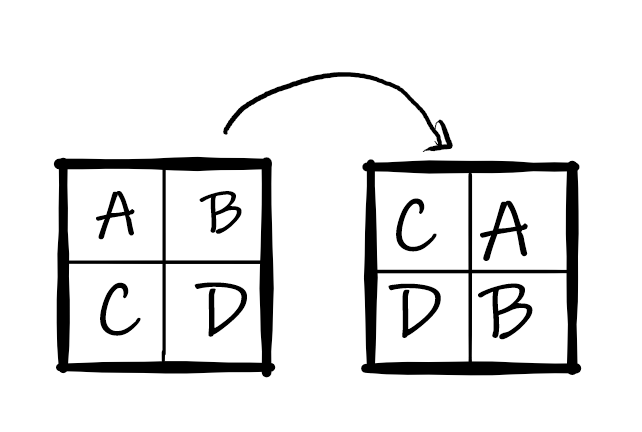
A, B, C et D sont des carrés.

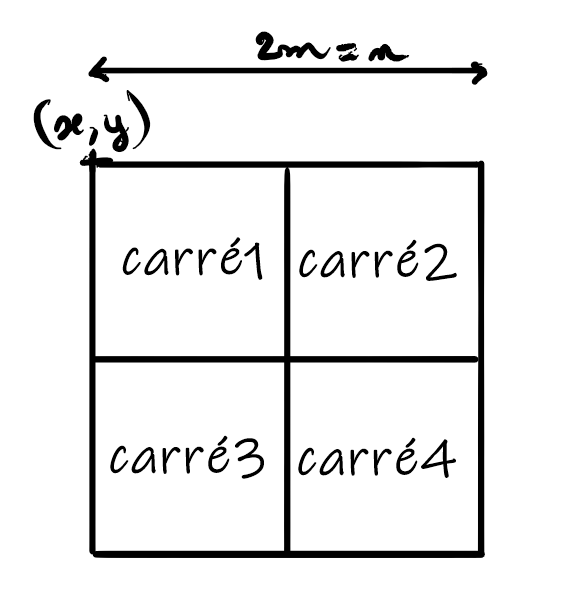
L'image est de taille $m\times m$. Le premier pixel de carré1 a pour coordonnées $(x ; y)$. Les quatre carrés ont la même dimension.

Donner les coordonnées du premier pixel des carré2, carré3 et carré4 en fonction de $x$, $y$ et $m$.

Écrire la procédure récursive tourneCarre(image,x,y,n) tourne d'un quart en sens horaire le carré de l'image de taille $n$ dont le premier pixel a pour coordonnées $(x,y)$.

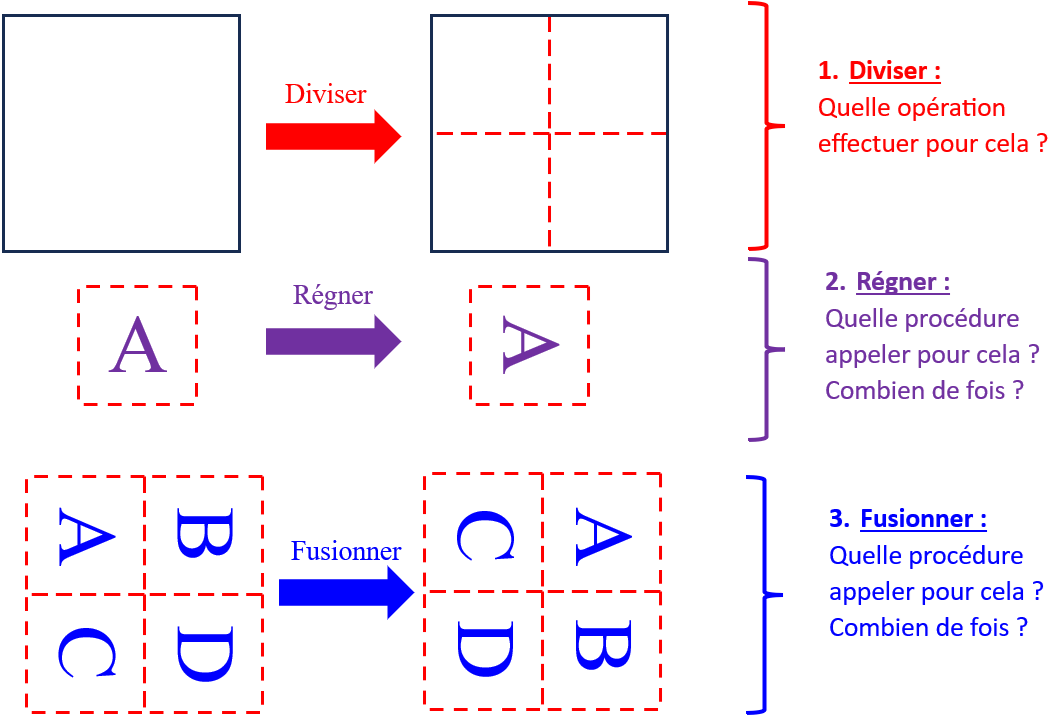
Écrire la fonction rotation(image,n) qui réalise la rotation de image de taille $n$ d'un quart de tour.

Vous pouvez visualiser l'effet de cet algorithme de quart de tour par diviser pour régner sur plusieurs images dans cette vidéo :

Nous avons vu deux algorithmes permettant de tourner une image carrée de taille une puissance de 2.

Nous avons vu que la complexité en temps de l'algorithme naïf est en $O(n^2)$.
Par contre, lors de cet algorithme naïf, il a fallu construire une seconde image de même taille pixel par pixel. Cela conduit donc à une complexité en mémoire en $O(n^2)$.
Pour l'algorithme suivant le paradigme diviser pour régner, ces deux complexités sont différentes.
Premièrement, la complexité en temps.
Si on étudie la procédure récursive tourneCarre, elle fait appel 4 fois à elle-même sur des images de taille réduite de 2 mais il y a aussi 3 appels à une procédure echangeCarre. Cette procédure echangeCarre contient 2 boucles for imbriquées. Sa complexité est en $O(n^2)$. Dès lors, on peut montrer par un calcul mathématique que la complexité en temps de la procédure tourneCarre est en $O(n^2\times \ln_2(n))$.
Cette complexité en temps est donc (un peu) moins bonne que celle de l'algorithme naïf.
Par contre, dans cette procédure, il n'y a pas de création d'une nouvelle image mais de simples permutations de pixels, un à un. La complexité en mémoire est donc ici en $O(1)$.
Cette complexité en mémoire en donc bien meilleure que celle de l'algorithme naïf.

Diviser pour régner est un paradigme de programmation qui consiste à ramener la résolution d'un problème à celle de un ou plusieurs sous-problèmes indépendants dont la taille est divisée.

On retrouve cette idée déjà vue dans la récursivité, sauf ici la taille est divisée et pas forcément réduite par soustraction.

Les algorithmes fondés sur le paradigmes diviser pour régner s'écrivent plus naturellement en récursif.

Ce paradigme de programmation permet dans certains cas de réduire la complexité en temps d'un algorithme ou la complexité en mémoire.

Exercices

Le but est d'utiliser le paradigme diviser pour régner pour calculer la puissance d'un nombre entier donné.

Nous avons vu dans l'exemple introductif à la récursivité, que l'on peut calculer la puissance $x^n$ par récursivité sous la forme $\begin{equation} x^n=\begin{cases} 1 & \text{si $n=0$}.\\ x \times x^{n-1} & \text{sinon}. \end{cases} \end{equation}$

Nous avions alors obtenu cet algorithme récursif :

def puissance_rec(x: float, n: int) -> float:
    if n == 0:
        return 1
    else:
        return x*puissance_rec(x, n-1)

La taille de la difficulté diminue de 1 à chaque appel. Cette diminution n'est pas optimale. On peut faire mieux en divisant la difficulté par 2 à chaque appel !

Pour cela, il suffit de remarquer que pour tout entiers naturels $x$ et $n$, on peut calculer $x^n$ ainsi : $\begin{equation} x^n=\begin{cases} 1 & \text{si $n=0$}.\\ (x\times x)^{\frac{n}{2}} & \text{si $n$ est pair et non nul}.\\ x \times (x\times x)^{\frac{n-1}{2}} & \text{si $n$ est impair}. \end{cases} \end{equation}$

À chaque appel, l'exposant est grosso modo divisé par 2, jusqu'à atteindre le cas simple où $n=0$.

Écrire une fonction récursive puissance_rapide qui prend en paramètres deux entiers $x$ et $n$, qui calcule $x^n$ en utilisant la remarque ci-dessus. Vous utilisez ainsi le paradigme "diviser pour régner".

Cliquer pour afficher la solution

def puissance_rapide(x: int, n: int) -> int:
    """
    n est un entier naturel non nul.
    Renvoie x^n calculé suivant le paradigme diviser pour régner
    """
    if n == 0:
        return 1
    elif n%2 == 0: # cas n pair et non nul
        return puissance_rapide(x*x, n/2)
    else:
        return x*puissance_rapide(x*x, (n-1)/2)

On peut mathématiquement montrer que :

la fonction récursive puissance_rec est de complexité en temps en $O(n)$ puisque l'on calcule successivement toutes les puissances de $x$ avec l'exposant variant entre 0 et $n$.
la fonction récursive puissance_rapide est de complexité en temps en $O(\ln_2(n))$.
Cette fonction est donc "infiniment" plus rapide que la précédente.

Ce paradigme de programmation est utilisé pour obtenir des algorithmes efficaces dans de nombreux domaines :

pour multiplier deux nombres de $n$ chiffres, l'algorithme de Karatsuba permet d'obtenir le résultat avec une complexité en temps inférieure à $O(n^2)$, la complexité en temps de l'algorithme naïf avec lequel vous multiplier à la main de nombres.
pour étudier des signaux numériques, l'algorithme de la Tranformée de Fourier Rapide permet d'obtenir une complexité en temps en $O(n\ln_2(n))$ au lieu de $O(n^2)$ pour l'algorithme naïf.

▲

Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲