
Problématique
L'objectif de ce cours est de réfléchir à la recherche de motifs dans une chaîne de caractères.
Autrement dit, il s'agit d'écrire des scripts qui permettent de vérifier qu'un motif (=mot, chaîne de caractères etc) se trouve à l'intérieur d'une chaîne de caractères.
-
Recherche du motif "CAG" dans la séquence protéinique suivante : "UAGGGUCGUCAGUAGUUCAAGUCUUCGACAGAGAGCUUC".
-
Le "Ctrl+F" qui permet de vérifier la présence d'un mot dans un un document numérique et sa position.
-
En Linux, la commande
grep motif nom_fichierpermet de rechercher une chaîne de caractèresmotifdans le contenu du fichiernom_fichier.
Dans ce chapitre nous traitons un algorithme qui s'approche de celui de Boyer Moore sans l'atteindre réellement au vu de sa complexité.
L'algorithme de Boyer-Moore est un algorithme de recherche de sous-chaîne particulièrement efficace. Il a été développé par Robert S. Boyer et J Strother Moore en 1977.
Cours réalisé à partir du document d'accompagnement sur cette partie du programme
Quelques notations et structures pour mettre en place l'algorithme.
Dans toute la suite on cherche la première occurrence d’un motif ( = chaîne de caractère) d'une longueur donnée dans un texte.
Définissons et nommons les variables qui vont nous être utile à l'écriture de l'algorithme:
Au cours de la recherche, on pose une fenêtre de taille long sur le texte, sur laquelle on aligne le motif.
On notera position la variable contenant l'index du caractère de texte qui est en face du premier élément de la fenêtre.
Enfin, nous notons j la variable contenant l'index du caractère du motif à comparer à un caractère du texte.
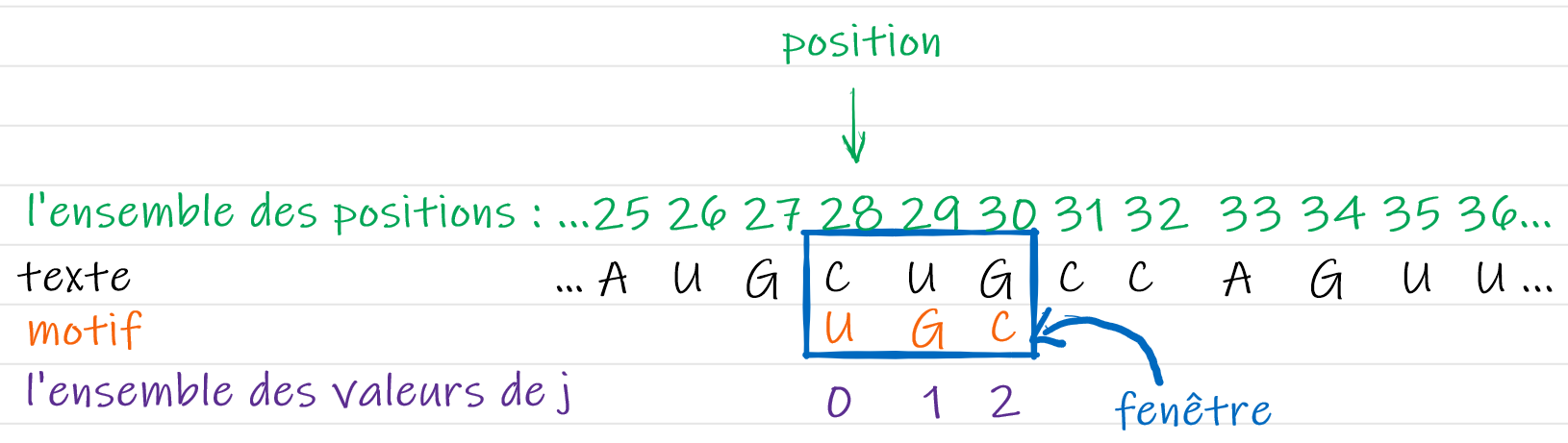
S'il n’y a pas correspondance entre le motif et la partie du texte que la fenêtre éclaire, on décalera la fenêtre avant de recommencer la comparaison.
Dans tous les algorithmes présentés ici, la fenêtre se déplacera toujours de gauche à droite.
Déterminer la longueur du texte, la valeur de position, les valeurs possibles pour j et la
valeur de long dans l'image suivante :

Même exercice avec l'image:

Avec les notations de la définition précédente, quel est le script qui permettra de comparer le caractère d'indice j dans le motif avec le caractère qui lui fait face dans le texte?
À quelle condition pourrons nous faire glisser la fenêtre de comparaison sur le texte ?
Écrire la réponse avec les notations précédentes.
Exprimer en fonction de position et long l'indice
du caractère du texte se trouvant en face du dernier caractère du motif.
L'algorithme Naïf
Écartons immédiatement l'usage du in de Python, qui renvoie simplement un booléen sans nous renseigner sur
la position du motif ou bien le nombre d'occurrences.
De plus, ce cours est un cours d'algorithme et le in est une facilité de Python qui peut nous éloigner de la comprehension complète de l'algorithme.
L’algorithme naïf consiste simplement à comparer un à un, de gauche à droite, les caractères du texte apparaissant dans la fenêtre avec ceux du motif. En cas de non-correspondance, on avance simplement la fenêtre d’une unité vers la droite.
Dans cet exercice, on veut écrire une fonction qui nous informe sur la correspondance du motif sur la partie du texte éclairée par la fenêtre ainsi que le décalage à appliquer.
-
Écrire une fonction
idem(texte, motif, position, long)qui renvoie un tuple constitué :-
d'un booléen
Truesi lemotifde longueurlongse trouve dans le chaîne de caractèrestexteà l'indexpositionetFalsesinon. -
d'un entier correspondant au décalage à appliquer : 1 si on n'a pas correspondance et 0 sinon.
Par exemple,
idem("veni vidi vici", "vi", 3, 2)renvoie le tuple(False, 1), maisidem("veni vidi vici", "vi", 10, 2)renvoie le tuple(True, 0). -
-
Écrire une fonction
rechercher(texte, motif)qui renvoie l'indice du premier caractère dumotifdans letextes'il est présent et -1 sinon. On utilisera la fonctionidemprécédente.Par exemple
rechercher("veni vidi vici", "vi")renvoie l'indice5
Le script suivant permet de charger le fichier text.txt:
fichier = open('text.txt', 'r')
texte = fichier.read()
fichier.close()
-
Télécharger Le soleil est toujours riant-Racine et Le Rouge et le noir.-Stendhal puis tester votre fonction
rechercherprécédente avec le motif"tel". -
Qu'observez vous?
Proposer au moins une précondition à la fonction rechercher
Algorithme de Horspool vers Boyer-Moore
Principe général
Au vu de la difficulté de l'algorithme de Boyer-Moore, commençons par comprendre la philosophie de cet algorithme compliqué au travers d'un algorithme de recherche textuel plus simple : l'algorithme de Horspool, qui est une simplification de celui de Boyer-Moore.
Nigel Horspool est né en Grande-Bretagne mais citoyen canadien. Il est professeur émérite d’informatique de l’université de Victoria. Il a conçu l'algorithme fin 1979 que nous décrivons maintenant.
-
La première idée consiste à comparer le
motifavec la portion dutextequi apparaît dans la fenêtre de droite à gauche, et non pas de gauche à droite. Ainsi, on fait décroîtrejà partir delong - 1tant que le caractèrey = motif[j]du motif et le caractère qui lui fait face dans le textex = texte[position + j]est identique. Par contre le texte est lui toujours lu de gauche à droite. -
La deuxième idée consiste à opérer le décalage de la fenêtre en fonction du caractère de la chaîne
textealigné avec le dernier caractère du motifmotif:-
Si ce caractère
texte[position + long - 1]est présent dans le motif, on décale le motif d'un saut vers la droite pour aligner ce caractère avec sa dernière occurrence dans le motif. -
Si ce caractère
texte[position + long - 1]n'est pas présent dans le motif, on décale le motif d'un saut de longueur du motif pour que le motif dépasse ce caractère.
-
Déroulement de l'algorithme de Horspool sur un exemple
La recherche textuelle est utilisée dans de nombreux domaines.
Par exemple, elle est utilisée en bio-informatique pour identifier des séquences ADN codées
par les lettres A, C, T, G qui représentent les bases nucléiques adénine, cytosine, thymine et guanine.
Considérons la protéine DMPK (Myotonin-Protein Kinase) qui joue un rôle crucial dans plusieurs processus cellulaires, notamment dans la régulation du glucose au niveau musculaire.
Cette protéine est synthétisée par l'organisme des homo sapiens à partir d'un gène se trouvant sur le chromosome 19.
Ce gène est comporte 19841 nucléotides et se termine par les 8 nucléotides ACTCCACT.
Sachant que l'on est en train de lire la portion du chromosome 19
GAAAAAGGACAGGGCCTGTGGCCACTCCACT, on aimerait repérer le motif
ACTCCACT dans cette portion afin de trouver la terminaison du gène.
Déroulons l'algorithme de Horspool sur cet exemple concret pour comprendre son fonctionnement :
Dans chacune des images de cet exemple, le dernier caractère du texte texte de la fenêtre de comparaison sera le caractère du texte sur fond bleu.
C'est sur ce caractère que l'on calcule le décalage à appliquer dans l'algorithme de Horspool.
Dans les images suivantes, le décalage fléché présent explicite le saut effectué depuis l'image précédente.
De plus, la position de la fin de la fenêtre de comparaison précédente est visible par la correspondance sous fond vert, concordance permise par le décalage.
Enfin, les symboles ❌ et ✅ explicitent le résultat des comparaisons de caractères effectuées depuis la droite de la fenêtre de comparaison.
-
Position initiale :
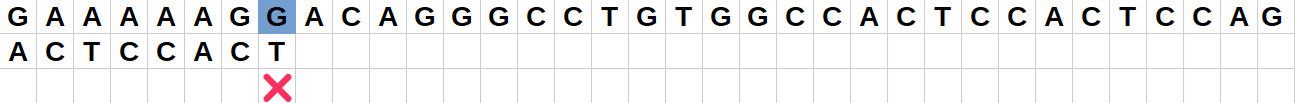
Le caractère "G" de la chaîne ne correspond pas au caractère final "T" du motif.
Comme ce caractère "G" n'est pas présent dans le motif, il est inutile de décaler le motif de 1 comme dans la version naïve : on va donc effectuer un saut de 8 vers la droite pour que le motif dépasse entièrement ce caractère "G". -
Position 2 :
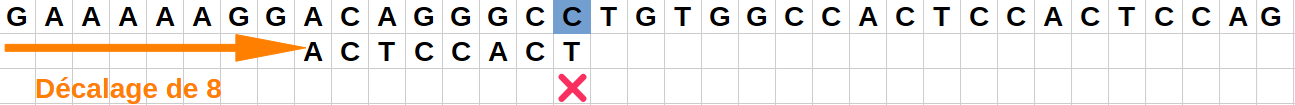
Le caractère "C" de la chaîne ne correspond pas au caractère final "T" du motif.
Comme ce caractère "C" est présent dans le motif en positionj=1,j=3,j=4etj=6, on peut décaler le motif pour mettre un caractère "C" en face de celui de la chaîne.
Comme on veut être sûr de tester tous les cas intéressants possibles, il est préférable de décaler au minimum le motif pour faire correspondre les "C" : on décale ainsi de sorte de faire correspondre le "C" avec le "C" le plus à droite du motif.
On va donc effectuer un saut de 1 vers la droite. -
Position 3 :

Les caractères "CT" de la chaîne correspondent aux caractères finaux "CT" du motif.
Cependant le caractère "C" précédent ne correspond pas au caractère "A" du motif.
Il faut encore décaler le motif, mais cette fois-ci pour mettre un "T" en face du "T" considéré de la chaîne.
Ce caractère "T" est présent dans le motif en positionj=2etj=7.
Comme le "T" en fin de motif correspond à la position actuelle ne convenant pas, on met en face du "T" de la chaîne celui du motif n'étant le caractère final.
On va donc effectuer un saut de 5 vers la droite. -
Position 4 :

Le caractère "C" de la chaîne ne correspond pas au caractère final "T" du motif.
Il faut encore décaler le motif pour mettre un "C" en face du "C" considéré de la chaîne.
Comme précédemment, il faut mettre le "C" le plus à droite du motif en face du "C" de la chaîne.
On va donc effectuer un saut de 1 vers la droite. -
Position 5 :
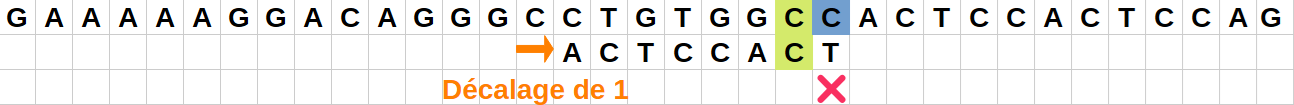
Le caractère "C" de la chaîne ne correspond pas au caractère final "T" du motif.
Il faut encore décaler le motif pour mettre un "C" en face du "C" considéré de la chaîne.
On va donc encore effectuer un saut de 1 vers la droite. -
Position 6 :

Le caractère "A" de la chaîne ne correspond pas au caractère final "T" du motif.
Il faut encore décaler le motif pour mettre un "A" en face du "A" considéré de la chaîne.
Comme le "A" le plus a droite du motif se trouve 2 rangs avant, on va donc effectuer un saut de 2 vers la droite. -
Position 7 :

Les caractères "CCACT" de la chaîne correspondent aux 5 derniers caractères du motif.
Le caractère "G" de la chaîne ne correspond pas au caractère "T" du motif.
Il faut encore décaler le motif pour mettre un "T" en face du "T" considéré de la chaîne.
On va donc effectuer un saut de 5 vers la droite. -
Position 8 :

Les caractères "ACTCCACT" de la chaîne correspondent aux 8 caractères du motif.
Le motif "ACTCCACT" cherché a donc été trouvé dans la chaîne.
Au niveau des étapes précédentes, chaque symbole ❌ ou ✅ correspond à une comparaison de caractères.
Il y a suffit ici de 22 comparaisons pour trouver le motif cherché avec l'algorithme de Horspool.
On peut calculer qu'il aurait fallu 39 comparaisons pour obtenir ce résultat avec l'algorithme naïf. On a donc réussi à obtenir le motif ici en en gros deux fois moins de calcul.
Vous trouverez dans dans ce document .txt l'ensemble des nucléotides de ce gène DMPK.
Calcul du décalage.
Dans l'exemple précédent, nous avons vu que les sauts sont déterminés par le caractère de la chaîne qui est aligné sur le dernier caractère du motif.
De plus, la valeur de ce saut est toujours le même pour un caractère donné :
-
Le caractère C conduit toujours à un décalage de 1.
-
Le caractère T toujours a un décalage de 5.
-
Le caractère A a un décalage de 2.
-
Le caractère G, comme tout caractère n'apparaissant pas dans le motif, a un décalage de 8, la longueur du motif.
Plutôt que de recalculer à chaque fois la valeur du saut à appliquer, il suffit d'effectuer un prétraitement au niveau de l'algorithme de Horspool en calculant au tout début la valeur du saut à effectuer pour chaque caractère.
On pourrait lors de ce prétraitement un tableau comme celui-ci :
| C | T | A | G ou autres |
| 1 | 5 | 2 | 8 |
En pratique, on implémente ce prétraitement sous forme d'un dictionnaire comme celui-ci :
pretraitement_sauts = {"C": 1, "T": 5, "A": 2}Les caractères n'apparaissant pas comme clé de ce dictionnaire conduise automatiquement à un saut correspondant à la longueur du motif.
Enfin, les valeurs associées à chaque caractère du motif peuvent être vues comme la distance entre le dernier caractère du motif et le représentant le plus à droite de ce caractère dans ce motif, hormis le dernier caractère du motif, d'où la propriété :
Lors du calcul du prétraitement des sauts, pour chaque lettre du motif (sauf la dernière), le
saut à effectuer est égal à l'écart entre la dernière occurrence de cette lettre dans le motif (sans prendre en compte le dernier caractère) et la fin du motif.
Attention ! On ne calcule pas de saut pour le dernier caractère.
On considère le motif cesser.
Déterminer à la main le dictionnaire obtenu par prétraitement de ce motif dans le cas où les valeurs sont les distances de la dernière occurrence du caractère avec le dernier caractère du motif.
Écrire une fonction pretraitement_motif(motif) qui renvoie un dictionnaire dont les clés sont les caractères
de la chaîne de caractères motif, sans prendre en compte le dernier caractère de
cette chaîne, et dont les valeurs sont la distance entre la dernière occurrence de ce caractère
avec le dernier de la chaîne motif.
Penser à tester la fonction proposée avec les chaînes de caractères "ACTCCACT" et "cesser", sans oublier que l'ordre d'affichage des associations
n'est pas important pour un dictionnaire.
idem version décalage
Dans cette partie, vous pouvez utiliser directement la fonction pretraitement_motif
de l'exercice précédent permettant d'obtenir un dictionnaire de sauts.
Ce dictionnaire sera alors utiliser
comme argument de fonctions pour éviter d'avoir à le recalculer à chaque appel de fonction.
-
Écrire une fonction
idem2(texte, motif, position, dico_decalages)qui renvoie un tuple constitué :-
d'un booléen
Truesi lemotifde longueurlongse trouve dans le chaîne de caractèrestexteà partir de l'indexposition; le booléen étantFalsesinon. -
d'un entier correspondant au décalage à appliquer (celui donné par le dictionnaire de prétraitement
dico_decalages).
Cet entier sera 0 si le motif est trouvé.
-
-
Vérifier la fonction
idem2en exécutant au moins les quatre tests ci-dessous :>>> idem2("GAAAAAGGACAGGGCCTGTGGCCACTCCACT", "ACTCCACT", 23, dico) (True, 0) >>> idem2("GAAAAAGGACAGGGCCTGTGGCCACTCCACT", "ACTCCACT", 8, dico) (False, 1) >>> idem2("GAAAAAGGACAGGGCCTGTGGCCACTCCACT", "ACTCCACT", 9, dico) (False, 5) >>> idem2("GAAAAAGGACAGGGCCTGTGGCCACTCCACT", "ACTCCACT", 0, dico) (False, 8)
Algorithme de Horspool
-
Écrire la fonction
rechercherqui implémente l'algorithme de Horspool.
Cette fonction :-
Commence par créer le dictionnaire de prétraitement du motif.
-
Balaie le texte de gauche à droite en effectuant des sauts si le motif ne correspond pas à la partie de texte considéré.
-
Utilise la fonction
idem2pour tester la correspondance et connaître l'éventuel décalage à effectuer. -
Renvoie soit le nombre -1 si le motif n'est pas trouvé, soit la position dans le texte du premier caractère du motif trouvé.
-
-
Vérifier que
rechercher("GAAAAAGGACAGGGCCTGTGGCCACTCCACT", "ACTCCACT")renvoie 23.
Bravo ! Vous avez réussi à comprendre et implémenter par étapes l'algorithme de Horspool !
Dans l'exercice suivant, vous pourrez l'écriture d'un seul tenant, hormis le prétraitement.
-
Compléter l'implémentation ci-dessous de l'algorithme de Horspool de sorte de renvoyer la liste (éventuellement vide) de toutes les positions où le motif
motifa été trouvé dans le textechaine:def dico_sauts(motif): d = ... for i in range(...): # Attention à bien exclure la dernière lettre du motif d[...] = ... return d def horspool(motif, chaine): # affiche le motif aligné avec la chaîne chaine pour visualiser les étapes faites et comprendre des erreurs print(chaine) print(' ' * i + motif) # Partie principale : comparaison(s) et décalage positions = [] n = len(chaine) long = len(motif) sauts = ... # Construction du dictionnaire gérant les sauts i = 0 while ...: j = long - 1 # Position du caractère étudié dans le motif carac_droite = chaine[...] # Caractère du texte en face du dernier caractère du motif while ... and chaine[...] == motif[...]: j = j - 1 if j == ...: # Cas où le motif a été trouvé positions.append(i) i = i + sauts[carac_droite] elif ...: # le caractère de droite n'est pas dans le motif mais SANS UTILISER ... in motif i = i + ... # saut effectué else: # le caractère de droite n'est pas dans le motif i = i + ... return positions -
Construire une fonction
testspermettant de vérifier les fonctionsdico_sautsethorspoolqui exécute au moins les quatre tests ci-dessous :assert dico_sauts("ACTCCACT") == {'A': 2, 'C': 1, 'T': 5}, "le prétraitement échoue avec la chaîne \"ACTCCACT\"." assert dico_sauts("ACT") == {'A': 2, 'C': 1}, "le prétraitement échoue avec la chaîne \"ACT\"." assert horspool("ACTCCACT", "GAAAAAGGACAGGGCCTGTGGCCACTCCACT") == [23], "échec premier test sur horspool" assert horspool("ACT", "A GALACTICA ACTA TA CATA. CA TRACTA TACTIC") == [5, 12, 31, 37], "échec deuxième test sur horspool" assert horspool("TATA", "A GALACTICA ACTA TA CATA. CA TRACTA TACTIC") == [], "échec troisième test sur horspool"
Complexité
Recherche naïve
Lors d'une recherche naïve, le pire des cas où le motif n'apparaît pas dans le texte
est celui où la différence entre le motif et le texte apparaît à chaque fois lors de la dernière
comparaison de caractères.
Par exemple, considérons texte = "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa...", texte où la lettre
"a" apparaît $n$ fois et motif = "aaa...ab", motif contenant $long$ caractères, que des "a" sauf le dernier.
Lors d'une telle recherche naïve de gauche à droite, pour chacun des $n-long+1$ premiers caractères de texte, il y aura $long$ comparaisons de caractères entre le texte et le motif.
Cela conduit à $(n-long+1)\times long$ comparaisons.
Une telle complexité est donc de l'ordre de $O(n\times long)$.
Lors d'une recherche naïve, le meilleur des cas où le motif n'apparaît pas dans le texte
est celui où la différence entre le motif et le texte apparaît à chaque fois lors de la première combinaison ; autrement dit, le cas où le motif commence par un caractère n'apparaissant jamais
dans le texte.
Lors d'une telle recherche naïve de gauche à droite, pour chacun des $n-long+1$ premiers caractères de texte, il y aura 1 comparaison de caractères entre le texte et le motif.
Cela conduit à $n-long+1$ comparaisons.
Une telle complexité est donc de l'ordre de $O(n)$.
Algorithme de Horspool
Le pire des cas où le motif n'apparaît pas dans le texte
est celui où la différence entre le motif et le texte apparaît à chaque fois lors de la dernière
comparaison de caractères.
Par exemple, considérons texte = "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa...", texte où la lettre
"a" apparaît $n$ fois et motif = "baaa...a", motif contenant $long$ caractères, que des "a" sauf le dernier.
Alors pour chacun des $n-long+1$ premiers caractères de texte, il y aura $long$ comparaisons de caractères entre le texte et le motif.
Cela conduit à $(n-long+1)\times long$ comparaisons.
Une telle complexité est donc encore de l'ordre de $O(n\times long)$.
Par contre, le meilleur des cas où le motif n'apparaît pas dans le texte
est celui où la différence entre le motif et le texte apparaît à chaque fois lors de la première combinaison ; autrement dit, le cas où le dernière caractère du texte mis en face du motif n'est
jamais dans le motif.
Alors, chaque comparaison conduit à un décalage complet du motif, c'est-à-dire d'un saut de $long$.
Ainsi, dans ce cas, il n'y aura que la partie entière de $\dfrac{n}{long}$ comme nombre de comparaisons.
Une telle complexité est donc de l'ordre de $O\left(\dfrac{n}{long}\right)$.
-
L'algorithme de Horspool n'améliore pas le pire des cas de la recherche naïve : le coût est toujours en $O(n\times long)$, où $n$ est la longueur du texte et $long$ celle du motif.
-
Dans le meilleur des cas d'un balayage complet, les sauts permettent de réduire le coût de l'algorithme de horspool en $O\left(\dfrac{n}{long}\right)$, ce qui bien mieux que la complexité dans le meilleur des cas de la recherche naïve : $O(n)$.
Bilan sur l'algorithme de Horspool
-
L'algorithme de Horspool est algorithme de recherche textuelle.
-
L'algorithme de Horspool commence par un prétraitement : On crée un dictionnaire dont les clés sont les lettres du motif (sauf la dernière) et les valeurs du saut à effectuer si le dernier élément du motif est en face de ce caractère.
-
La valeur du saut correspond à la distance entre la dernière occurrence de ce caractère dans le motif et la fin du motif.
-
L'algorithme de Horspool consiste à comparer les caractères du motif avec ceux de la chaîne un par un en remontant de droite à gauche dans le motif jusqu'à trouver une différence.
-
Quand une différence est trouvée, on regarde le caractère de la chaîne aligné sur le dernier caractère du motif :
-
Si ce caractère est présent dans le motif, on décale le motif d'un saut (dont la valeur est donnée par le dictionnaire) pour aligner ce caractère de la chaîne avec sa dernière occurrence dans le motif (sans compter le caractère final du motif).
-
Si ce caractère n'est pas présent dans le motif (ou seulement en dernière position), on décale le motif d'un saut de la longueur du motif pour dépasser ce caractère.
-
-
L'algorithme de Horspool n'améliore pas le pire des cas de la recherche naïve : le coût est toujours en $O(n\times long)$, où $n$ est la longueur du texte et $long$ celle du motif.
-
Dans le meilleur des cas d'un balayage complet, les sauts permettent de réduire le coût en $O\left(\dfrac{n}{long}\right)$, ce qui bien mieux que la complexité dans le meilleur des cas de la recherche naïve : $O(n)$.
Algorithme de Boyer Moore
Maintenant que vous maîtrisez l'algorithme de Horspool qui est une version simplifiée de celui de
Boyer-Moore, vous êtes prêt.e.s pour découvrir cet algorithme plus compliqué.
Cette partie dépasse les attendus du programme de NSI.
Principes généraux de l'algorithme
-
Comme pour l'algorithme de Horspool, la première idée consiste à comparer le
motifavec la portion dutextequi apparaît dans la fenêtre de droite à gauche. Ainsi, on fait décroîtrejà partir delong - 1tant que le caractèrey = motif[j]du motif et le caractère qui lui fait face dans le textex = texte[position + j]est identique. Par contre le texte est lui toujours lu de gauche à droite. -
La deuxième idée consiste à effectuer deux prétraitements qui permettre de décider du décalage de la fenêtre en cas de non-correspondance :
-
Le premier prétraitement permet de mettre en place la règle du premier caractère différent depuis la droite.
-
Le second prétraitement permet de mettre en place la règle du bon suffixe qui dépend du nombre de caractères vérifiés avec succès.
-
Déroulement du principe de la règle du premier caractère différent sur un exemple
Reprenons la recherche du motif ACTCCACT dans le texte
GAAAAAGGACAGGGCCTGTGGCCACTCCACTCCAG.
Dans chacune des images de cet exemple, le premier caractère différent sera le caractère du texte sur fond bleu.
C'est sur ce caractère que l'on calcule le décalage à appliquer, contrairement à Horspool où on regarde toujours celui du texte mis en face du dernier caractère du motif !
Dans les images suivantes, le décalage fléché présent explicite le saut effectué depuis l'image précédente.
De plus, la position de la fin de la fenêtre de comparaison précédente est visible par la correspondance sous fond vert, concordance permise par le décalage.
Enfin, les symboles ❌ et ✅ explicitent le résultat des comparaisons de caractères effectuées depuis la droite de la fenêtre de comparaison.
-
Position initiale :
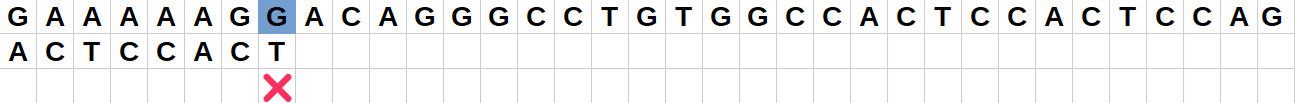
Le caractère "G" de la chaîne ne correspond pas au caractère final "T" du motif.
Comme ce caractère "G" n'est pas présent dans le motif, comme pour Horspool, on va donc effectuer un saut de 8 vers la droite pour que le motif dépasse entièrement ce caractère "G". -
Position 2 :
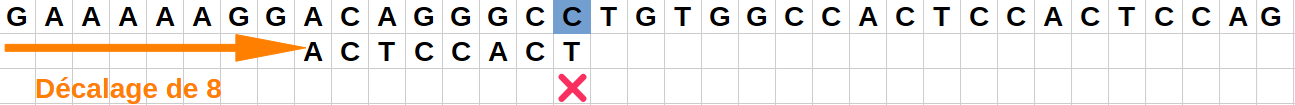
Le caractère "C" de la chaîne ne correspond pas au caractère final "T" du motif.
Comme ce caractère "C" est présent dans le motif à droite du caractère de discordance et comme il est préférable de décaler au minimum le motif pour faire correspondre les "C" : on décale ainsi de sorte de faire correspondre le "C" avec le "C" le plus à droite du motif.
Comme pour Horspool ici, on va donc effectuer un saut de 1 vers la droite. -
Position 3 :

Les caractères "CT" de la chaîne correspondent aux caractères finaux "CT" du motif.
Cependant le caractère "C" précédent ne correspond pas au caractère "A" du motif : la discordance se fait au niveau du caractère "C" du motif : c'est le premier caractère différent.
Il faut encore décaler le motif, mais cette fois-ci pour mettre un "C" en face du premier caractère différent.
Ce caractère "C" est présent dans le motif en positionj=1,j=3,j=4etj=6.
Comme il ne faut ni reculer le motif, ni sauter des cas possibles, il suffit de mettre en correspondance le premier caractère différent "C" avec le "C" du motif que l'on rencontre le premier à sa gauche dans le motif : ici, c'est celui en positionj=4, c'est-à-dire, celui à un rang vers la gauche.
On va donc effectuer un saut de 1 vers la droite.
On peut remarquer que pour cette position particulière ceci est moins bon que le décalage obtenu avec Horspool. -
Position 4 :

Le caractère "G" de la chaîne ne correspond pas au caractère final "T" du motif : ici le premier caractère différent rencontré est le caractère "G".
Comme le "G" n'est pas dans le motif, il suffit de décaler pour dépasser ce caractère.
On va donc effectuer un saut de 8 vers la droite. -
Position 5 :

Les 5 premiers caractères correspondent. Ici, le caractère "G" de la chaîne ne correspond pas au caractère "T" du motif.
Il faut encore décaler le motif pour dépasser ce "G" absent du motif.
On va donc effectuer un saut de 3 vers la droite.
Il faut remarquer ici que le même caractère discordant, ici "G", conduit dans les deux dernières étapes à deux décalages différents : contrairement à Horspool, dans Boyer-Moore on n'associe pas un unique décalage à un caractère. -
Position 6 :

Le caractère "A" de la chaîne ne correspond pas au caractère final "T" du motif : c'est le premier caractère différent.
Il faut encore décaler le motif pour mettre un "A" en face du "A" considéré de la chaîne.
Parmi les "A" à gauche, le plus a droite du motif se trouve 2 rangs avant, on va donc effectuer un saut de 2 vers la droite. -
Position 7 :

Les caractères "ACTCCACT" de la chaîne correspondent aux 8 caractères du motif.
Le motif "ACTCCACT" cherché a donc été trouvé dans la chaîne.
Au niveau des étapes précédentes, chaque symbole ❌ ou ✅ correspond à une comparaison de caractères.
Il y a suffit ici de 21 comparaisons pour trouver le motif cherché avec cette méthode de Boyer-Moore avec le principe de premier caractère différent.
Ainsi, même si à au moins une étape, le décalage a été moins pertinent que celui permis par Horspool, on obtient finalement ici le résultat avec très légèrement moins de calculs.
Table de décalage pour la règle du premier caractère différent
À la différence de Horspool, les décalages ne dépendent pas que d'un seul caractère dans la chaîne (celui en face du dernier caractère du motif), dans l'algorithme Boyer Moore utilisant la règle du premier caractère différent, les décalages dépendent du premier caractère différent et de sa position dans le motif.
La table des décalages doit donc désormais avoir deux entrées :
-
les caractères du motif qui pourraient apparaître comme le premier caractère différent,
-
la position
jà laquelle ils se trouveraient dans le motif.
Voici la table de décalages, incomplète, associée à l'algorithme de Boyer Moore où on applique uniquement la règle du premier caractère différent :
-
les lignes correspondents aux positions
jpossibles dans le motif, en précisant entre parenthèse le caractère considéré, -
les colonnes correspondent au premier caractère différent possible,
-
les valeurs au décalage à appliquer lorsqu'il y a différence,
-
la croix X signifie qu'il n'y a pas de différence pour ce caractère donc que ce n'est pas le premier caractère différent pour ce cas.
-
Le symbole ... correspond aux cases incomplètes du tableau qu'il faudra compléter dans l'exercice suivant cet exemple.
| A | C | T | Autre | |
|---|---|---|---|---|
| 0 (A) | X | 1 | 1 | 1 |
| 1 (C) | 1 | X | 2 | 2 |
| 2 (T) | ... | ... | ... | ... |
| 3 (C) | 3 | X | 1 | 4 |
| 4 (C) | ... | ... | ... | ... |
| 5 (A) | X | 1 | 3 | 6 |
| 6 (C) | ... | ... | ... | ... |
| 7 (T) | 2 | 1 | X | 8 |
Explications pour quelques lignes :
-
Ligne "0 (A)" :
Si le premier caractère différent est le A tout à gauche du motif, on a la configuration suivante :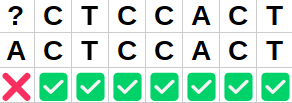
Quel que soit donc le caractère noté ? (différent de A) de la chaîne, il faudra appliquer un décalage de 1 pour dépasser ce caractère différent ne se trouvant plus à gauche dans le motif. -
Ligne "1 (C)" :
Si le premier caractère différent est le C, avant dernier à gauche du motif, on a la configuration suivante :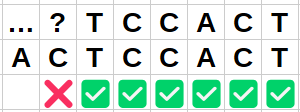
Pour le caractère noté ? (différent de C) de la chaîne, il y a deux cas :-
Si le premier caractère différent ? est un A : il faudra appliquer un décalage de 1 pour le faire coïncider avec le A tout au gauche du motif.
-
Pour tout les autres caractères, il faut dépasser ce caractère ? donc appliquer un décalage de 2.
-
-
Ligne "3 (C)" :
Si le premier caractère différent est le C en positionj=3, on a la configuration suivante :
Pour le caractère noté ? (différent de C) de la chaîne, il y a trois cas :-
Si le premier caractère différent ? est un A : il faudra appliquer un décalage de 3 pour le faire coïncider avec le A tout au gauche du motif.
-
Si le premier caractère différent ? est un T : il faudra appliquer un décalage de 1 pour le faire coïncider avec le T juste à gauche.
-
Pour tout les autres caractères, il faut dépasser ce caractère ? donc appliquer un décalage de 4.
-
Compléter les lignes manquantes de la table de décalages de l'exemple précédent en s'aidant des explications données précédemment.
On peut implémenter cette table de décalages en Python :
-
soit avec un tableau 2D, c'est-à_dire une liste de listes,
-
soit avec une liste de dictionnaires.
Voyons comment implémenter la table de décalages avec une liste de dictionnaires.
Comme chaque ligne de la table correspond à un entier allant de 0 à long - 1, cet entier correspond à l'indice du dictionnaire implémentant l'information de la ligne.
Comme mettre "autre" comme clé du dictionnaire est peut pertinent lors des tests, il est préférable de considérer que "par défaut", le décalage à appliquer sera celui qui permettra que le motif dépasse le caractère différent considéré. Ainsi, pour le dictionnaire de la ligne j, le décalage par défaut est j + 1.
Il suffit donc pour chaque dictionnaire de préciser les associations liant le caractère possible du motif à un décalage différent de j + 1. Ainsi, la table de l'exemple précédent peut être implémentée par :
[{},
{"A": 1},
{"A": 2, "C": 1},
{'A': 3, 'C': 2, 'T': 1},
{'A': 4, 'C': 1, 'T': 2},
{'A': 5, 'C': 1, 'T': 3},
{'A': 1, 'C': 2, 'T': 4},
{'A': 2, 'C': 1, 'T': 5}]
Vous pouvez vérifier sur des exemples que si on reprend la fonction pretraitement_motif utilisé dans Horspool :
def pretraitement_motif(motif: str) -> dict:
"""
motif: str
renvoie un dictionnaire dont les clés sont les caractères
de la chaîne de caractères motif et les valeurs l'écart minimal de la clé avec le dernier caractère
"""
pre = {}
long = len(motif)
for i in range(long-1): # long - 1 pour ne pas prendre en compte le dernier caractère.
pre[motif[i]] = long - 1 - i# écart entre l'index du dernier élément (long -1) avec celui du caractère
return prealors la liste de dictionnaires permettant d'implémenter la table de décalages permettant de prendre en compte la règle du premier caractère différent peut être obtenue par le programme ci-dessous :
def table_decalage_1carac_diff(motif: str) -> list[dict]:
"""
motif est une chaîne de caractère
Renvoie un tableau de dictionnaires de décalages.
L'indice j du dictionnaire dans le tableau correspond
à la position en face du premier caractère différent dans le motif.
"""
tab = []
for j in range(len(motif)):
tab.append(pretraitement_motif(motif[:j+1])) # :j+1 pour balayer le motif de 0 à j.
return tab
Proposer une fonction table_decalage_1carac_diff2 qui prend
en paramètre une chaîne de caractères motif et qui renvoie
la table de décalages, sans appeler directement la fonction pretraitement_motif.
Combiner les scripts des fonctions pretraitement_motif et
table_decalage_1carac_diff en une seule fonction.
Algorithme de Boyer Moore avec la règle du premier caractère différent
Avec ce prétraitement, on peut écrire alors l'algorithme de Boyer Moore simplifié où le ne prend en compte que la règle du premier caractère différent, algorithme qui renvoie ici la liste de toutes les positions du premier caractère d'une occurrence du motif dans le texte :
def boyer_moore(motif: str, texte: str) -> list:
positions = []
n = len(texte)
long = len(motif)
decalages = table_decalage_1carac_diff(motif) # on construit la liste de dictionnaires table de décalages
i = 0
while i + long <= n : # Même condition qu'à l'exercice 4 : le motif ne doit pas dépasser la fin du texte
# pour visualiser l'étape considérée avec le texte et le motif positionné
print(texte)
print(' ' * i + motif)
j = long - 1 # position du caractère dans le motif
while j >= 0 and texte[i + j] == motif[j]:
j = j - 1
# si on a trouvé le motif
if j == -1:
positions.append(i) # rajout dans la liste des positions d'occurrences trouvées
i = i + 1 # décalage pour chercher une nouvelle occurrence ensuite
# sinon cas où le premier caractère différent est dans le motif à gauche
elif texte[i + j] in decalages[j]: # le premier caractère différent est texte[i + j]
i = i + decalages[j][texte[i + j]] # on décale à droite suivant la table de décalages
# sinon cas où le premier caractère différent n'est pas dans le motif à gauche
else:
i = i + j + 1 # on décalage de j+1 pour que tout le motif dépasse le premier caractère différent
return positions
# tests : à rajouter lors de l'exercice ci-dessous
Tester l'algorithme de Boyer Moore simplifié précédent avec le motif
ACTCCACT et le texte GAAAAAGGACAGGGCCTGTGGCCACTCCACTCCAG.
Vous devez retrouver les étapes décrites lors du déroulé de l'algorithme de Boyer Moore avec la règle du premier caractère différent.
Tester ensuite sur un motif plusieurs présent dans une chaîne de caractères.
Règle du bon suffixe
Le bon suffixe est l'ensemble des caractères du motif se trouvant à droite du premier caractère discordant (en comparant depuis la droite de la fenêtre).
Voici différents exemples de bon suffixe :
Dans chacune des images de cet exemple, le bon suffixe sera le ou les caractères du texte sur fond orangé.
C'est sur cette chaîne de caractères que l'on calcule le décalage à appliquer.
De plus, les symboles ❌ et ✅ explicitent le résultat des comparaisons de caractères effectuées depuis la droite de la fenêtre de comparaison.
-
Dans ce cas, le bon suffixe est la chaîne "CT", le caractère "C" devant est le premier caractère discordant :

-
Dans ce cas, le bon suffixe est la chaîne "CCACT", le caractère "G" devant est le premier caractère discordant :
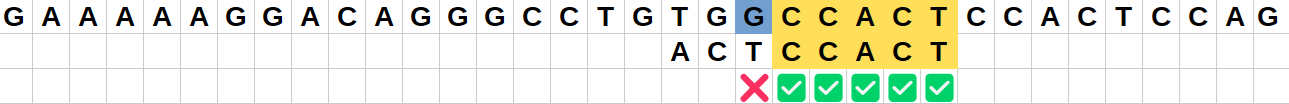
-
Dans ce cas, le bon suffixe est la chaîne vide "", le caractère "G" tout à droite est le premier caractère discordant :
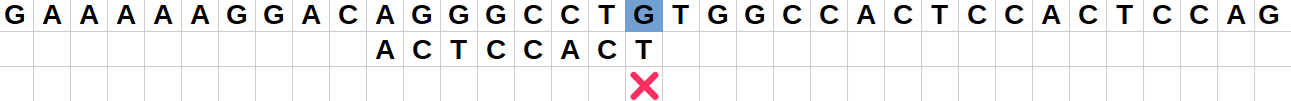
Utilisation de la règle du bon suffixe sur un exemple
Supposons encore que l'on cherche désormais le motif ACTCCACT dans la chaîne de caractères modifiée GAAAAAGGACTGGGCCTGTGGCCACTCCACTCCAG.
Voyons comment utiliser la règle du bon suffixe sur plusieurs cas :
-
Supposons être dans la situation suivante :

Le bon suffixe est "T", précédé du premier caractère discordant "G".
En ne regardant ici que le bon suffixe, tout décalage ne dépassant pas ce bon suffixe doit mettre coïncidence ce bon suffixe avec un autre "T".
La seule possibilité ici est la suivante :

Or, ce décalage conduirait à mettre en face du premier caractère discordant un "C", c'est à dire le même caractère que celui qui a posé problème initialement.
Ainsi, si le bon suffixe est un "T", il faut forcément effectuer un décalage de 8 pour dépasser ce bon suffixe :

-
Supposons être dans la situation suivante :

Le bon suffixe est "CT", précédé du premier caractère discordant "C".
En ne regardant ici que le bon suffixe, tout décalage ne dépassant pas ce bon suffixe doit mettre coïncidence ce bon suffixe avec un autre "CT".
La seule possibilité ici est la suivante :

Or, ce décalage conduirait à mettre en face du premier caractère discordant un "A", c'est à dire le même caractère que celui qui a posé problème initialement.
Ainsi, si le bon suffixe est un "CT", il faut là encore forcément effectuer un décalage de 8 pour dépasser ce bon suffixe :

-
Supposons être dans la situation suivante :
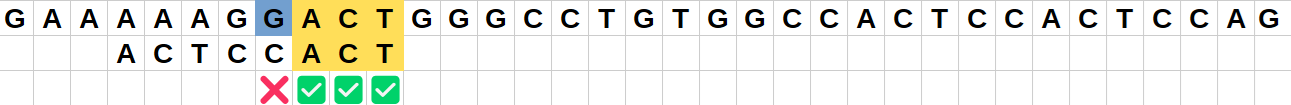
Le bon suffixe est "ACT", précédé du premier caractère discordant "G".
En ne regardant ici que le bon suffixe, tout décalage ne dépassant pas ce bon suffixe doit mettre coïncidence ce bon suffixe avec un autre "ACT".
La seule possibilité ici est la suivante :
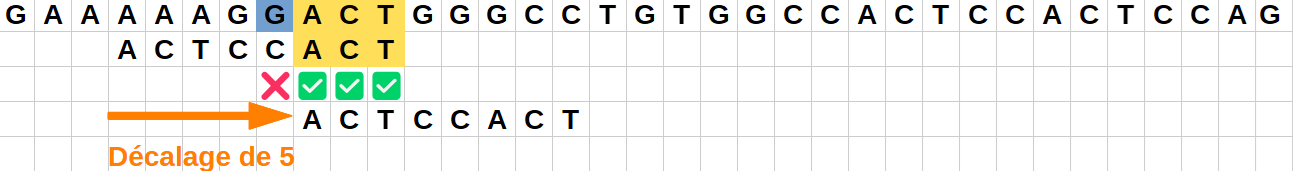
Ce décalage est possible .
Ainsi, si le bon suffixe est un "ACT", il faut dans ce cas effectuer un décalage de 5 pour mettre le bon suffixe en correspondance avec une chaîne identique.
Table de décalage pour la règle du bon suffixe
Dans l'exemple précédent, on peut se rendre compte que le décalage lié au bon suffixe ne dépend en fait que du motif et non du texte dans lequel on recherche.
On devine ainsi l'énoncé suivant explicitant la règle du bon suffixe :
Règle du bon suffixe :
Quand une discordance de caractères est trouvée, on regarde les caractères de la chaîne à droite du premier caractère discordant depuis la droite, c'est le bon suffixe.
-
Si ce bon suffixe est présent dans le motif à gauche du bon suffixe et que le caractère le précédant est différent de celui précédant le bon suffixe, on décale le motif pour aligner ce bon suffixe avec sa prochaine occurrence dans le motif (depuis la droite).
-
Sinon, on décale le motif de la longueur du motif pour dépasser ce bon suffixe.
De plus, on peut résumer les trois cas de l'exemple précédent dans un tableau associatif le décalage à appliquer suivant le bon suffixe trouvé dans le motif ACTCCACT :
|
Bon suffixe |
"T" |
"CT" |
"ACT" |
|---|---|---|---|
|
Décalage à appliquer |
8 | 8 | 5 |
Compléter le tableau associatif précédent pour traiter les autres bons suffixes possibles dans le motif :
|
Bon suffixe |
"" |
"T" |
"CT" |
"ACT" |
"CACT" |
"CCACT" |
"TCCACT" |
"CTCCACT" |
"ACTCCACT" |
|---|---|---|---|---|---|---|---|---|---|
|
Décalage à appliquer |
... | 8 | 8 | 5 | ... | ... | ... | ... | ... |
En réalité, l'énoncé de la règle du bon suffixe ne fonctionne pas dans tous les cas tel quel.
Pour le découvrir, étudions l'exemple suivant :
Supposons encore que l'on cherche désormais le motif modifié ACTCCAC dans la chaîne de caractères initial GAAAAAGGACAGGGCCTGTGGCCACTCCACTCCAG.
Supposons être dans ce cas :
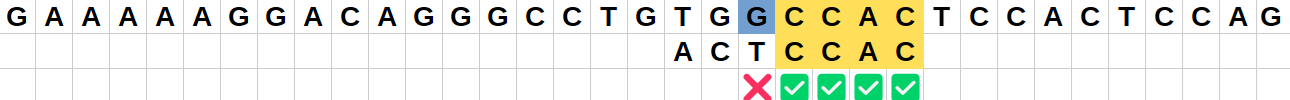
Le bon suffixe est "CCAC", précédé du premier caractère discordant "G".
En ne regardant ici que le bon suffixe, tout décalage ne dépassant pas ce bon suffixe doit mettre coïncidence ce bon suffixe avec un autre "CCAC".
Il n'y a pas de "CCAC" précédant le bon suffixe dans le motif.
Cependant, la fin du bon suffixe correspond au début de ce motif ;
on peut donc décaler ce motif de sorte à faire correspondre ces parties :

Ainsi, si le bon suffixe est un "CCAC", il faut effectuer un décalage de 5 pour retrouver une concordance.
L'idée pour que l'énoncé de la règle du bon suffixe reste pertinent est de faire précéder
le motif de len(motif)-1 caractères jokers $.
Ces caractères sont en concordance avec n'importe quel caractère du texte :

On peut aussi améliorer l'énoncé de la règle du bon suffixe ainsi :
Règle du bon suffixe :
Quand une discordance de caractères est trouvée, on regarde les caractères de la chaîne à droite du premier caractère discordant depuis la droite, c'est le bon suffixe.
-
Cas 1 : présence d'une instance précédente du bon suffixe
Si ce bon suffixe est présent dans le motif à gauche du bon suffixe et que le caractère le précédant est différent de celui précédant le bon suffixe, on décale le motif pour aligner ce bon suffixe avec sa prochaine occurrence dans le motif (depuis la droite). -
Cas 2 : présence d'un suffixe du bon suffixe comme préfixe
Si ce bon suffixe n'est pas entièrement présent dans le motif à gauche du bon suffixe mais seulement la fin de ce bon suffixe au début du motif , on décale le motif pour aligner cette fin du bon suffixe (le suffixe du bon suffixe) avec le début similaire du motif. -
Cas 3 : autres cas
Sinon, on décale le motif de la longueur du motif pour dépasser ce bon suffixe.
On considère dans cet exercice le motif ATTCAT et la chaîne
de caractères ATGCCATGCCTCATTCATG.
-
Expliciter la succession de positions de la fenêtre lors d'une recherche de ce motif en appliquant la règle du bon suffixe uniquement avec un décalage de 1 par défaut lorsque le bon suffixe est vide.
-
Déterminer le tableau associatif donnant le décalage à appliquer en fonction du bon suffixe.
Implémentation de la table de décalage pour la règle du bon suffixe
Voici une implémentation possible de la table de décalage pour la règle du bon suffixe, en s'appuyant sur les 3 cas vue au niveau de la dernière version de la règle du bon suffixe :
Dans ce prétraitement, deux tableaux sont utilisés :
-
Le dernier cas est traité par défaut (cf. ligne 4).
-
Le premier cas est traité à partir de la ligne 22.
-
Le deuxième cas est traité entre les lignes 14 et 20
def pretraitement_bon_suffixe(motif: str) -> list:
m = len(motif)
# liste donnant les décalages à appliquer en fonction de la position du premier caractère discordant (m positions possibles : celles entre 0 et m-1)
decalages = [m] * m # Par défaut décalage de la longueur du motif
# cas particulier pour le dernier symbole du motif
# Si discordance au dernier, le bon suffixe est vide : décalage de 1
decalages[m-1] = 1
# Si le premier caractère discordant est en position i (< m-1)
# alors le bon suffixe commence en position i+1
# et a une longueur maximale de m - i - 1
# calcul du plus grand préfixe qui est également suffixe (sans être le motif tout entier)
for i in range(m-2, -1 ,-1): # balayage depuis la droite sans prendre le dernier
for j in range(0, m - i-1): # balayage des longueurs possibles
# on vérifie que la fin du motif (entre m-(j+1) et m)
# est identique au début du motif(entre 0 et j+1)
if motif[0:j+1] == motif[m-(j+1):m]:
decalages[i] = m-(j+1) # décalage
# recherche d'une autre occurrence du suffixe à gauche de celui-ci
# On veut celle la plus à droite
i = m - 2
while i >= 0:
# motif à rechercher
recherche = motif[i+1:m] # le suffixe comment en position i+1
long = len(recherche) # longueur du suffixe recherché
# on cherche le motif depuis la droite afin d'avoir celui le plus à droite s'il existe
k = i
while k >= 0:
# cas où le bon suffixe est trouvé précédemment
# soit au tout début, soit avec un caractère précédent différent
# du caractère ayant conduit à la discordance
if motif[k:k+long] == recherche and (k == 0 or motif[k-1] != motif[i]):
decalages[i] = i - k + 1
k = -1 # pour forcer l'arrêt de la recherche : l'occurrence la plus à droite est trouvée
k = k - 1
i = i - 1
return decalages -
Tester la fonction
pretraitement_bon_suffixedans le cas des motifs"ACTCCACT"et"ATTCAT". -
Vérifier la cohérence avec les tableaux associatifs obtenus à l'exercice 16 et à l'exercice 17.
-
Vérifier que
pretraitement_bon_suffixe("GATCAT")renvoie la liste[6, 6, 6, 3, 6, 1]et quepretraitement_bon_suffixe("TACTGTACTTACT")renvoie la liste[9, 9, 9, 9, 9, 9, 9, 9, 4, 12, 12, 3, 1]
L'implémentation précédente est loin d'être optimale.
Il existe une implémentation bien plus efficace mais comprendre
pourquoi elle fonction nécessite de comprendre la notion de "frontière"
d'une chaîne de caractères, ce qui est largement hors programme.
Si vous désirez comprendre pourquoi l'implémentation suivante convient,
vous pouvez consulter site en anglais
def regle_bon_suffixe(motif):
m = len(motif)
# Tableau pour stocker les décalages
decalages = [0] * (m + 1)
# Tableau pour stocker les frontières
frontieres = [0] * (m + 1)
i = m
j = m + 1
frontieres[i] = j
while i > 0:
while j <= m and motif[i - 1] != motif[j - 1]:
# Cas 1 : Le bon suffixe est présent ailleurs dans le motif
if decalages[j] == 0:
decalages[j] = j - i
j = frontieres[j]
i -= 1
j -= 1
frontieres[i] = j
# Cas 2 : Le bon suffixe n'est pas entièrement présent, mais un suffixe du suffixe l'est
j = frontieres[0]
for i in range(m + 1):
if decalages[i] == 0:
decalages[i] = j
if i == j:
j = frontieres[j]
# Cas 3 : Aucun cas précédent ne s'applique, on décale de la longueur du motif
# (Cela est implicitement géré par les valeurs par défaut de décalage)
return decalages Boyer Moore complet
Voici enfin une implémentation de Boyer Moore intégrant les deux règles vues, celle du premier caractère discordant et celle du bon suffixe :
def pretraitement_bon_suffixe(motif: str) -> list:
m = len(motif)
# liste donnant les décalages à appliquer en fonction de la position du premier caractère discordant (m positions possibles : celles entre 0 et m-1)
decalages = [m] * m # Par défaut décalage de la longueur du motif
# cas particulier pour le dernier symbole du motif
# Si discordance au dernier, le bon suffixe est vide : décalage de 1
decalages[m-1] = 1
# Si le premier caractère discordant est en position i (< m-1)
# alors le bon suffixe commence en position i+1
# et a une longueur maximale de m - i - 1
# calcul du plus grand préfixe qui est également suffixe (sans être le motif tout entier)
for i in range(m-2, -1 ,-1): # balayage depuis la droite sans prendre le dernier
for j in range(0, m - i-1): # balayage des longueurs possibles
# on vérifie que la fin du motif (entre m-(j+1) et m)
# est identique au début du motif(entre 0 et j+1)
if motif[0:j+1] == motif[m-(j+1):m]:
decalages[i] = m-(j+1) # décalage
# recherche d'une autre occurrence du suffixe à gauche de celui-ci
# On veut celle la plus à droite
i = m - 2
while i >= 0:
# motif à rechercher
recherche = motif[i+1:m] # le suffixe comment en position i+1
long = len(recherche) # longueur du suffixe recherché
# on cherche le motif depuis la droite afin d'avoir celui le plus à droite s'il existe
k = i
while k >= 0:
# cas où le bon suffixe est trouvé précédemment
# soit au tout début, soit avec un caractère précédent différent
# du caractère ayant conduit à la discordance
if motif[k:k+long] == recherche and (k == 0 or motif[k-1] != motif[i]):
decalages[i] = i - k + 1
k = -1 # pour forcer l'arrêt de la recherche : l'occurrence la plus à droite est trouvée
k = k - 1
i = i - 1
return decalages
def pretraitement_caractere_discordant(motif: str) -> list[dict]:
tab = []
for j in range(len(motif)):
pre = {}
long = len(motif)
for i in range(j):
pre[motif[i]] = j - i
tab.append(pre)
return tab
def boyer_moore_complet(motif: str, texte: str) -> list:
mauvais_caracteres = pretraitement_caractere_discordant(motif)
bons_suffixes = pretraitement_bon_suffixe(motif)
positions = []
n = len(texte)
m = len(motif)
i = 0 # balayage du texte par la gauche
while i <= n - m: # non dépassement du texte
# pour visualiser l'étape considérée avec le texte et le motif positionné
print(texte)
print(' ' * i + motif)
j = m - 1 # balayage du motif par la droite
while j >= 0 and motif[j] == texte[i + j]: # comparaison du motif et du texte de la fenêtre
j -= 1
if j < 0: # motif entièrement trouvé
positions.append(i) # solution à rajouter
i += bons_suffixes[0] # décalage après une occurrence trouvée
else:
# décalage obtenu avec la règle du premier caractère discordant
if texte[i + j] in mauvais_caracteres[j]:
decalage1 = mauvais_caracteres[j][texte[i + j]]
else:
decalage1 = j + 1 # décalage par défaut pour les clés absentes du dictionnaires mauvais_caracteres[j]
# décalage obtenu avec la règle du bon suffixe
decalage2 = bons_suffixes[j]
# décalage à appliquer : le plus grand des deux décalages trouvés
i += max(decalage1, decalage2)
return positions-
Tester la fonction précédente proposée
boyer_moore_completavec le motif"ACTCCACT"et le texte"GAAAAAGGACAGGGCCTGTGGCCACTCCACTCCAG". -
Modifier la fonction
boyer_moore_completafin d'afficher le nombre de comparaison de caractères nécessaire pour trouver le motif"ACTCCACT"dans le texte"GAAAAAGGACAGGGCCTGTGGCCACTCCACTCCAG". -
Vérifier que 15 comparaisons de caractères et 5 décalages suffisent dans ce cas, ce qui est bien mieux que ce que l'on avait obtenu avec la version de Horspool (22 comparaisons et 7 décalages) ou avec Boyer Moore avec la seule règle du premier caractère différent (21 comparaisons et 6 décalages) ou avec la méthode naïve (39 comparaisons et 23 décalages).
Exercices du baccalauréat
On suppose disposer d'une fonction recherche(mot, texte) qui renvoie
True si une chaîne de caractères mot est présente dans
une chaîne de caractères texte et False sinon.
Expliquer succinctement le principe de l'algorithme de Boyer-Moore qui permet
d'implémenter cette fonction recherche.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International