Clin œil à Stéphane ROEBROECK 😉

Réalisez les figures suivantes avec le module turtle

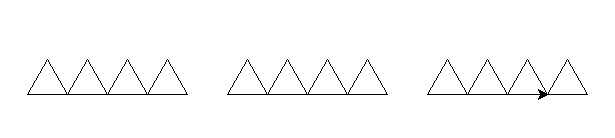
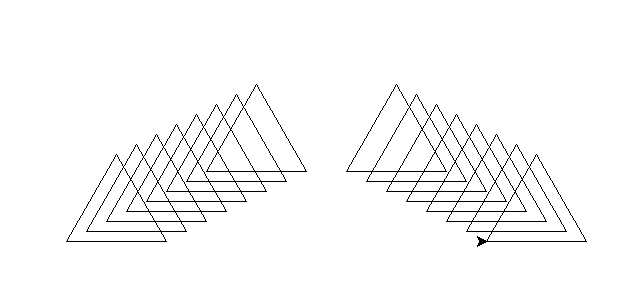
Tester et utiliser le code suivant :

import turtle
turtle.speed('fast')


def carre(x,y,c):
    """
    à partir du point de coordonnées (x;y) et de côté c (points)"""
    turtle.up() #lève le stylo
    turtle.goto(x,y) #se rend sur le point de coordonnées (x;y)
    turtle.down() #descend le stylo
    for i in range(4):
        turtle.forward(c)
        turtle.left(90)



carre(-100,-100,50)
turtle.mainloop() # Pour sortir en python

# turtle.exitonclick()
# Pour sortir en jupyter
# Attention en jupyter il faut forcer l'exécution une deuxième fois

			

Un TP (difficile mais au rendu très chouette) proposé par un enseignant de la liste de diffusion NSI (Adrien WILLM)

Une vidéo comme consigne :

Le TP à télécharger : téléchargement ici

Pour vous aider, le dessin du sol et deux rectangles.

import turtle

from random import randint, shuffle

def couleur_aleatoire():
    turtle.colormode(255)
    r = randint(0,255)
    g = randint(0,255)
    b = randint(0,255)
    return (r,g,b)

def trait(x1,y1,x2,y2):
    '''
    Paramètres
        x1, y1 : coordonnées du début du trait
        x2, y2 : coordonnées de la fin du trait
    '''
    turtle.penup()
    turtle.goto(x1,y1)
    turtle.pendown()
    turtle.goto(x2,y2)

def rectangle(x,y,w,h):
    '''
    Paramètres
        x, y : coordonnées du centre de la base de rectangle
        w : largeur du rectangle
        h : hauteur du rectangle
    '''
    turtle.penup()
    turtle.goto(x-w/2,y)
    turtle.pendown()
    turtle.goto(x+w/2,y)
    turtle.goto(x+w/2,y+h)
    turtle.goto(x-w/2,y+h)
    turtle.goto(x-w/2,y)


# ----- Sol de la rue -----
def sol(y_sol):
    '''
    Paramètres
        y_sol : ordonnée du sol du la rue
    '''
    turtle.pensize(3)
    trait(-380, y_sol, 380, y_sol)


# ----- Le programme -----

if __name__ == "__main__":
    turtle.setup(800, 600)
    turtle.speed(0)
    turtle.hideturtle()

    y_sol = -200
    # Dessin du sol de la rue
    sol(y_sol)

    rectangle(-100,y_sol,100,200)

    rectangle(100,y_sol,50,300)

    turtle.exitonclick()

A vous de créer des fonctions :

• pour le dessin du toit, facade, immeuble,etc.
• pour le dessin des fenêtres, portes, balcons,etc.
• Soyez créatif ...

Vous pouvez vous répartir le travail et travailler en mode coopératif

Un autre TP (difficile) pour utiliser le module turtle comme simulateur de déplacements d'un robot.

Vous trouverez en vidéo le rendu des simulations :

Pour vous aider, le dessin de la pièce.

# -*- coding:utf-8 -*-
from math import *
from random import *
import matplotlib.pyplot as plt
import numpy as np

from turtle import * 
clear()

# structure en listes P pour pièce, O pour obstacle, R pour repère
# Les obstacles sont modélisés par des rectangles.

P0=(0,0)
P1=(200,0)
P2=(200,300)
P3=(0,300)
piece=[P0,P1,P2,P3]

O11=(170,130)
O12=(200,130)
O13=(200,180)
O14=(170,180)
Obstacle1=[O11,O12,O13,O14]

O21=(120,220)
O22=(200,220)
O23=(200,270)
O24=(120,270)
Obstacle2=[O21,O22,O23,O24]

O31=(0,100)
O32=(50,100)
O33=(50,200)
O34=(0,200)
Obstacle3=[O31,O32,O33,O34]


O41=(150,0)
O42=(200,0)
O43=(200,50)
O44=(150,50)

Obstacle4=[O41,O42,O43,O44]

Po0=(0,220)
Po1=(10,220)
Po2=(10,290)
Po3=(0,290)

Porte=[Po0,Po1,Po2,Po3]

C11=(140,210)
C12=(180,210)
C13=(180,220)
C14=(140,220)

Chaise1=[C11,C12,C13,C14]


C21=(110,225)
C22=(120,225)
C23=(120,265)
C24=(110,265)

Chaise2=[C21,C22,C23,C24]

# Les point repères

R0=(10,10)
R1=(100,60)
R2=(100,180)
R3=(60,250)


# Les points objectifs

O1=(120,270)
O2=(120,220)
O3=(10,250)
O4=(150,30)



# Structure en dictionnaire
# piece={'A':(0,0),'B':(200,0),'C':(200,300),'D':(0,300)}
# Obstacle3={'O31':(0,100),'032':(50,100),'033':(50,200),'034':(0,200)}


def X(point):
    return point[0]

def Y(point):
    return point[1]

def distance(A,B):
    return sqrt((B[0]-A[0])**2+(B[1]-A[1])**2)

def DessinerSegment(A,B):
    up()
    goto(A[0],A[1])
    down()
    goto(B[0],B[1])


def  DessinerPoygone(liste):
    listeTemp=liste
    listeTemp.append(listeTemp[0])
    up()
    goto(X(liste[0]),Y(liste[0]))
    down()
    for k in range(len(liste)-1):
        A=listeTemp[k]
        B=listeTemp[k+1]
        DessinerSegment(A,B)

def DessinerPiece():
    DessinerPoygone(piece)
    DessinerPoygone(Porte)
    DessinerPoygone(Obstacle3)
    DessinerPoygone(Obstacle2)
    DessinerPoygone(Obstacle1)
    DessinerPoygone(Obstacle4)
    DessinerPoygone(Chaise1)
    DessinerPoygone(Chaise2)

def initialiser(x,y):
    up()
    goto(x,y)
    down()

def DeplacementAleatoire(x,y):
    """Attention, il n'y a pas de tests de bords de la pièce dans ce déplacement
    """
    L=([-20,-10,0,10,20])
    d1=choice(L)
    d2=choice(L)
    return x+d1,y+d2


DessinerPiece()
exitonclick()