Code de déblocage du chapitre :

Demander le programme !

BO sd5

Graphe non-orienté

Exemple introductif

Vous avez décidé d'essayer de créer un réseau social Types_au_top. Pour cela, vous avez réuni vos bons amis proches et vous leur avez demandé à chacun d'en parler à leurs propres amis proches. Pour simplifier, on note A, B, ..., G et H les 8 personnes acceptant de faire partie de votre réseau social Types_au_top. Voici la liste des relations entre ces individus :

Malgré la faible taille de votre réseau social actuel, vous vous rendez-compte que sa description deviendra vite très obscure s'il grandi fortement, comme vous l'espérez.

Un des amis de votre réseau vous propose de visualiser votre réseau social ainsi :

  1. Chaque membre du réseau sera modélisé par un point nommé par une lettre,

  2. chaque relation entre deux amis sera modélisé par un trait reliant les points représentant les amis.

Afin d'illustrer sa proposition, votre ami vous propose le schéma suivant :

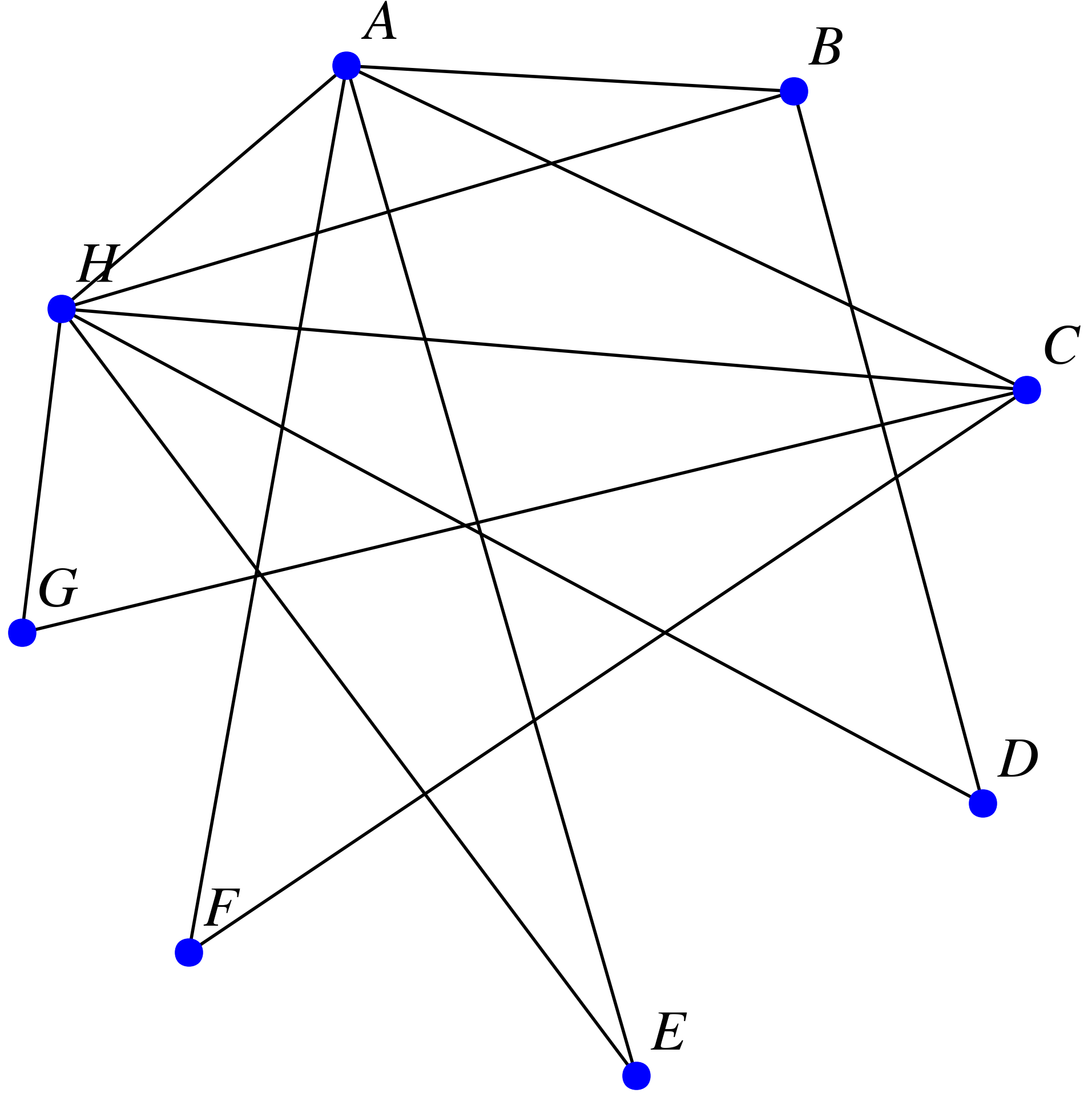
schéma du réseau social

Ce type de représentation s'appelle un graphe (non-orienté). Ce qui est bien c'est que ce cours va détailler cette notion et que l'on verra, aussi dans un autre chapitre, des algorithmes pour les étudier. Quelle chance pour votre réseau social ! Vive la NSI !

Pour les curieux, voici le problème historique qui a conduit au développement initial des graphes.

La ville de Königsberg était une ville de Prusse puis une des principales villes de l'Empire Allemand avant d'être céder à l'URSS en 1945. Cette ville est désormais appelée Kaliningrad et fait partie de la Fédération de Russie.

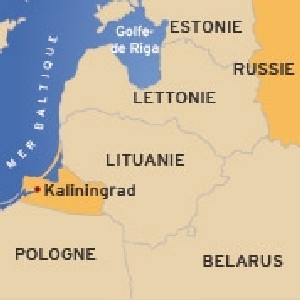
localisation

Cette ville s'étendait au $XVIII^e$ siècle autour de deux îles situées sur le fleuve Pregel. Ces deux îles étaient reliées entre elles par un pont. Six autres ponts reliaient les rives de la rivière à l'une ou l'autre des deux îles, comme représenté sur le plan ci-dessous.

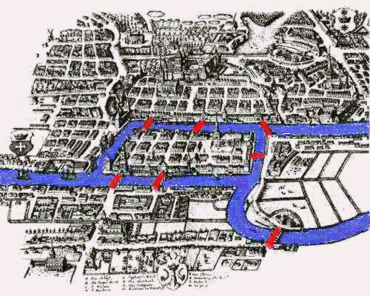
pont de Könisberg

La légende raconte que certains habitants de cette ville cherchaient lors de promenade à passer une fois et une seule par chacun des ponts pour revenir au point de départ (évidemment, ils ne pouvaient traverser l'eau du Pregel qu'en passant par un des ponts.)

Est-ce possible ? Si oui, par quel chemin ?

Les habitants ont cherché des solutions et l'un d'eux, le grand mathématicien Euler, a réussi en 1735 à répondre à la question précédente. Pour cela, il a développé des outils mathématiques à la base de la théorie des graphes, théorie qui sera effleurée dans ce cours.

Modélisation à l'aide d'un graphe :

Une des idées d'Euler fut de modéliser la situation pour réduire à l'essentiel le problème ; il a représentée la configuration précédente des ponts dans la ville en la figure ci-dessous :

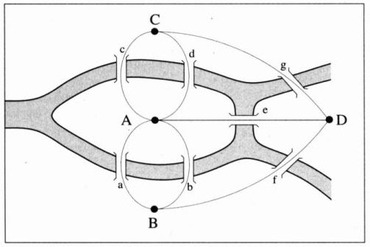
modélisation par un graphe

figure qui peut être déformée ainsi :

modélisation clarifiée par un graphe

Vocabulaire sur les graphes non-orientés

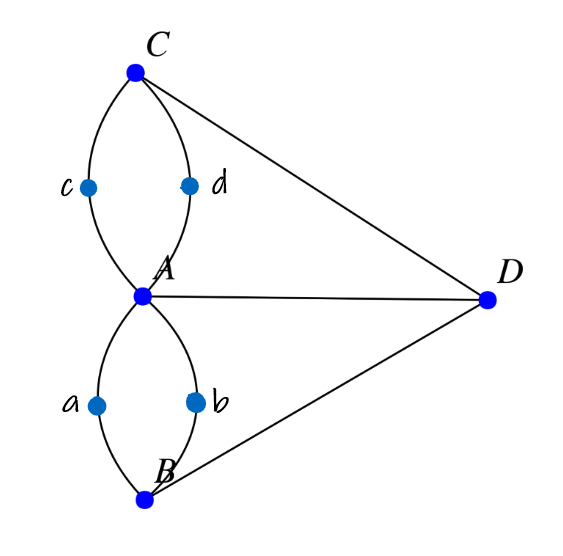
Voici ci-dessous un graphe non-orienté qui représente une modélisation possible du problème des ponts de Königsberg expliqué dans la remarque historique.

modélisation Köenigsberg

  1. Donner deux sommets adjacents du graphe ci-dessus.

  2. Donner deux sommets non adjacents du graphe ci-dessus.

  3. Le graphe ci-dessus est-il un graphe complet ? Pourquoi ?

  4. Comment rendre le graphe ci-dessous complet ?

Code de déblocage de la correction :

Un des amis de votre réseau travaille pour un distributeur d'électricité.

Il doit proposer à son supérieur une représentation du réseau reliant différentes villes.
Comme il n'y arrive pas trop, il voudrait que vous la lui fassiez.

Pour simplifier le problème, il a déjà renommé les villes en A, B, C, D, E et F. De plus, il vous donne les informations suivantes :

  1. Proposer un graphe qui modélise la situation.

  2. Ce graphe est-il complet ? Pourquoi ?

Code de déblocage de la correction :

modélisation Köenigsberg

  1. Quel est l'ordre de ce graphe ?

  2. Quel est le degré du sommet $A$ ?

  3. Lister les sommets de degré 3 de ce graphe.

Code de déblocage de la correction :

exercice de renforcement

Liste d'adjacence

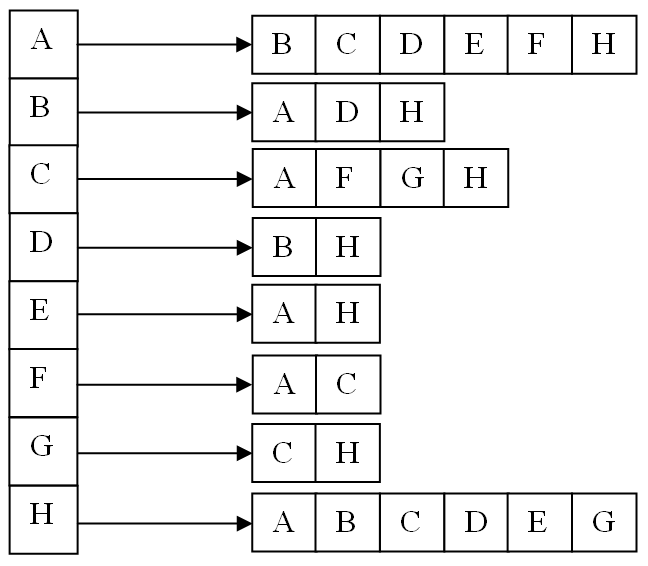
Il est possible de considérer un graphe comme une liste de sommets, liste où on associe à chaque élément la liste des sommets liés à cet élément.

Reprenons l'exemple introductif. L'ensemble des relations :

peut être vu comme une liste d'adjacence :

vision sous forme de liste de listes.

graphe non-orienté en langage Python

En s'inspirant des listes d'adjacence d'un graphe vues ci-dessus, une façon d’encoder un graphe sous Python est d’utiliser un dictionnaire : les clés seront les sommets du graphe et leur valeur sera la liste des sommets adjacents.

Reprenons le graphe introductif :

schéma du réseau social

Le code suivant permet d'implémenter un graphe en langage Python


graphe = dict()    # création d'un dictionnaire vide 
graphe["A"] = ["B", "C", "E", "F", "H"] # liens de A vers les sommets listés
graphe["B"] = ["A", "D", "H"]
graphe["C"] = ["A", "F",  "G", "H"]
graphe["D"] = ["B", "H"]
graphe["E"] = ["A", "H"]
graphe["F"] = ["A", "C"]
graphe["G"] = ["C", "H"]
graphe["H"] = ["A", "B", "C", "D", "E", "G"]

Rappels :

Vous avez vu l'an dernier dans le cours sur les dictionnaires, qu'il est possible :

  1. En s'aidant de la remarque précédente, proposer une fonction ordre en langage Python qui reçoit en paramètre un dictionnaire et renvoie l'ordre de ce graphe.

  2. Tester votre fonction ordre en utilisant le graphe de l'exemple introductif, implémenté en langage Python ci-dessus.

Code de déblocage de la correction :

  1. Écrire une fonction sommets_adjacents qui prend en paramètre un dictionnaire ainsi qu'un sommet sous forme de chaîne de caractères et qui renvoie la liste des sommets adjacents à ce sommet entré comme paramètre.

  2. Tester la fonction sommets_adjacents sur le sommet $A$.

  3. Proposer des préconditions.

  4. Proposer une fonction lister_aretes qui prend en paramètre un dictionnaire et renvoie la liste des arêtes d'un graphe. Une arête sera représentée par un tuple à deux éléments. ( Attention aux doublons)

Code de déblocage de la correction :

exercice de renforcement

Parcours sur un graphe non-orienté

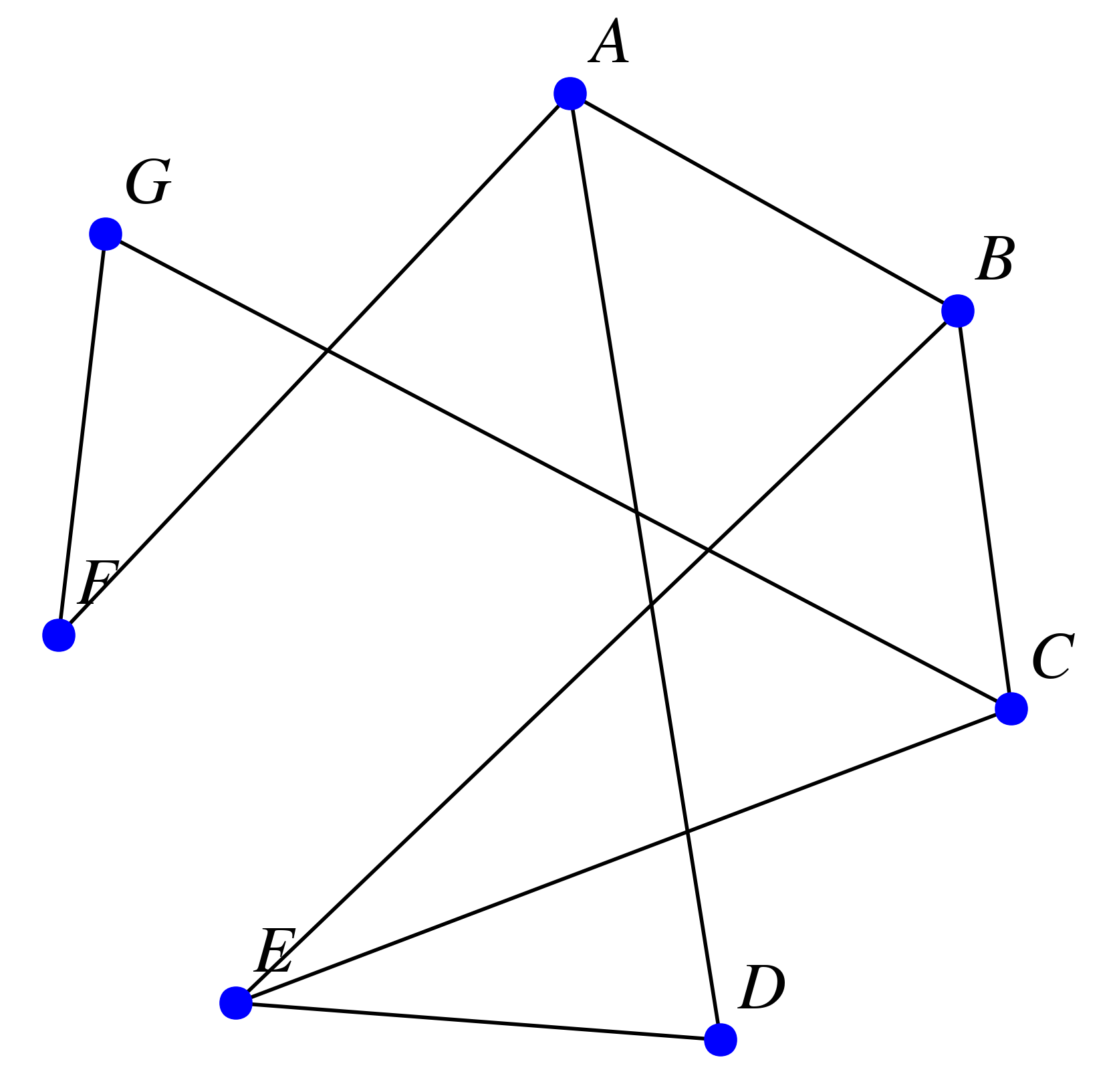
On considère le graphe non-orienté suivant :

graphe

  1. Quel est l'ordre du graphe ?

  2. Quel nom peut porter la chaîne $B - C - E - B$ ? Quelle est sa longueur ?

  3. Déterminer une chaîne de longueur 8 reliant $E$ à $A$

  4. Déterminer un cycle d'origine $G$.

  5. Le graphe est-il connexe ?

Code de déblocage de la correction :

Proposer un graphe qui n'est pas connexe.

Code de déblocage de la correction :

exercice de renforcement

Dans un prochain chapitre, nous verrons comment des algorithmes permettant de parcourir un graphe, de trouver un cycle, ... Patience !

Graphe orienté

Exemple de graphe orienté

Voici une carte où sont positionnées 6 lieux notés A, B, C, D, E et F dans le centre ville de Vitry-le-François.

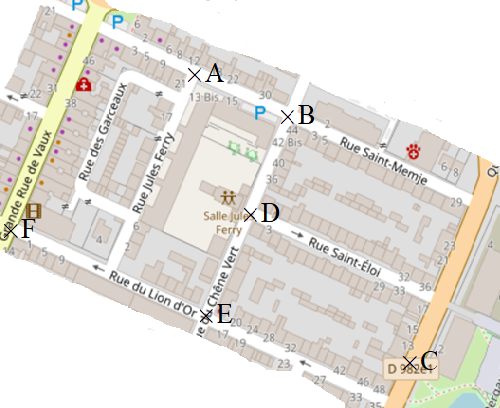
graphe exo renf 1

On cherche à modéliser les trajets possibles simples permettant de relier directement en voiture ces positions : pour cela on utilise encore un graphe.

Cependant, comme il y a des sens unique, certains trajets ne peuvent se faire que dans un sens. On va donc utiliser des flèches pour modéliser un trajet possible entre deux points. On obtient ainsi le graphe suivant :

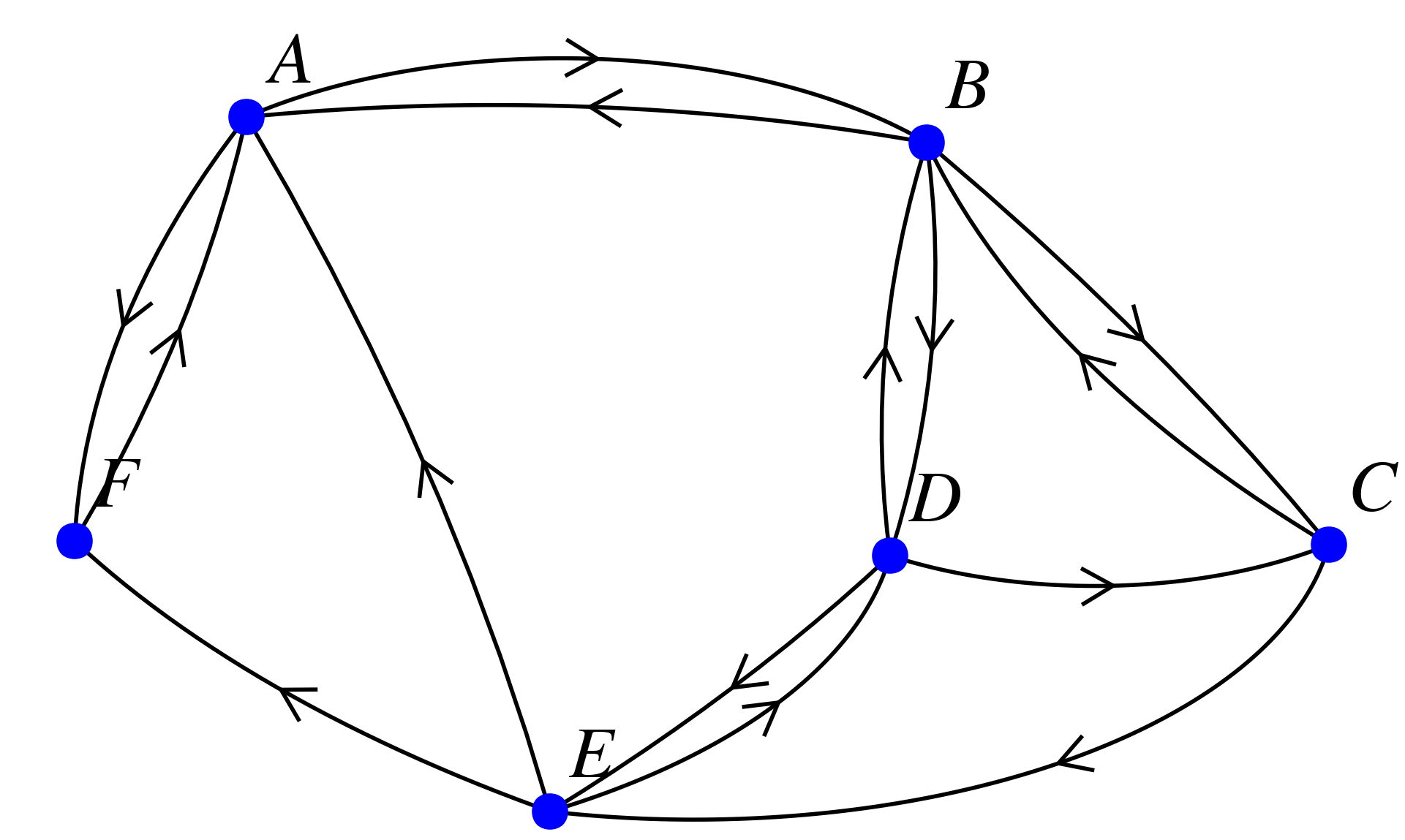
modélisation lieux de Vitry

Ce type de graphe est appelé un graphe orienté.

Vocabulaire

Proxémie des termes suivant l'orientation ou non du graphe :

Graphe non-orienté Graphe orienté
arête arc
chaîne chemin
cycle circuit

Voici de nouveau le graphe d'introduction :

modélisation lieux de Vitry

Le graphe suivant représente le plan d’une ville. Les arcs du graphe représentent ses avenues commerçantes, en prenant en compte le sens de circulation, et les sommets du graphe les carrefours de ces avenues.

bac ES métropole septembre 2017

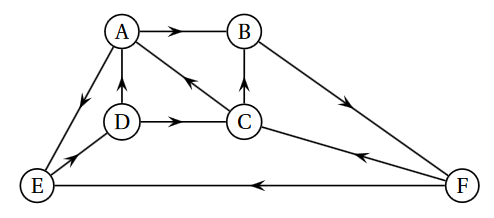
  1. Est-ce un graphe orienté ou non-orienté ? Pourquoi ?

  2. Quel est l'ordre du graphe ?

  3. Proposer un chemin de longueur 4 d'origine $F$ et d'extrémité $B$.

  4. Proposer un circuit passant par tous les sommets.

Code de déblocage de la correction :

exercice de renforcement

Bibliothèque networkx

Le but de cette partie est d'étudier le graphe orienté précédent sur Python.

bac ES métropole septembre 2017

Nous utiliserons la bibliothèque networkx.

Pour implémenter le graphe de l'exercice précédent, il vous suffit de saisir progressivement les instructions suivantes :

  1. Commencer par importer le module networkx, sous l'alias nx ici.

    Importer aussi le module matplotlib.pyplot, sous l'alias plt ici, afin de pouvoir tracer le graphe implémenté.

    Code de déblocage de la correction :

  2. Créer un graphe orienté vide avec le script nx.DiGraph():

    Code de déblocage de la correction :

  3. Ajouter au graphe chaque sommet (appelé node) avec la méthode add_node:

    Code de déblocage de la correction :

  4. Ajouter au graphe chaque arc (appelé edge) avec la méthode add_edges_from:

    Code de déblocage de la correction :

    Pour ajouter à un graphe non-orienté des arêtes, il suffit d'utiliser la méthode add.edges au lieu de add.edges_from.

  5. Pour visualiser le graphe utiliser ce script:

    nx.draw(graphe, node_size=800, node_color='blue', edge_color='red', with_labels=True)
plt.show()   # pour visualiser le graphique créé

    Vous devez voir apparaître une fenêtre contenant une figure proche de celle-ci :

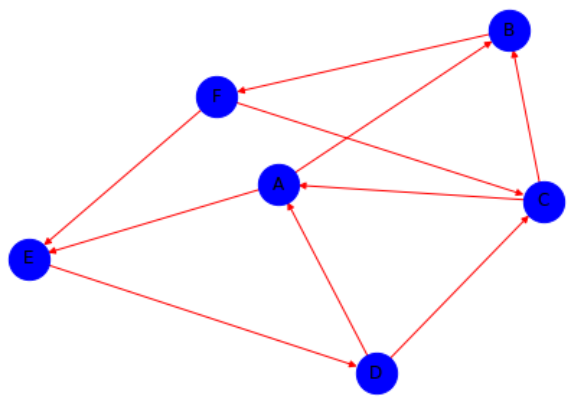
    reseau à voir

    • Les flèches correspondent aux traits plus épais de la liaison entre dans deux sommets.

    • Il est possible d'intégrer séparément sous forme d'un dictionnaire toutes les options du tracé du graphique ainsi :

      # ensemble des options
options = {
            'node_size' : 800,   # taille des sommets
            'node_color' : 'blue', # couleur de fond des sommets
            'edge_color' : 'red', # couleur des arcs
            'with_labels' : 'True',  # avec le nom des sommets 
          }                                    
nx.draw(graphe, **options)
plt.show()   # pour visualiser le graphique créé

      Cela permet entre autre de définir une fois pour toutes les caractéristiques des tracés pour les utiliser pour chacun des graphes : il y a alors une cohérence dans la présentation générale.

Pour des compléments et des précisions sur l'utilisation du module networkx, vous pouvez consulter :

exercice de renforcement

La bibliothèque networkx contient aussi différentes méthodes portant sur les graphes, sommets et arcs :

Une documentation complète est disponible à cette adresse.

Utiliser les méthodes et fonctions de la bibliothèque networkx pour :

  1. obtenir le degré du sommet 'A' du graphe de l'exercice précédent.

    Code de déblocage de la correction :

  2. obtenir le nombre de sommets de ce graphe.

    Code de déblocage de la correction :

  3. obtenir le nombre d'arcs de ce graphe.

    Code de déblocage de la correction :

  4. obtenir la liste des sommets voisins au sommet 'D' de ce graphe.

    le type de l'objet renvoyé peut dépendre de l'IDLE utilisé : sous Edupython, l'objet renvoyé est de type list tandis que sous jupyter c'est un itérateur dict_keyiterator. Ne pas hésiter dans ce seconde cas à transtyper sous forme de liste l'itérateur obtenu avec la méthode successors afin de lire plus facilement l'ensemble renvoyé.

    Code de déblocage de la correction :

  5. Tester aussi la méthode successors avec :

    graphe.successors('E')

    Ne pas hésiter à transtyper si besoin sous forme de liste l'itérateur obtenu avec la méthode successors afin de lire plus facilement l'ensemble renvoyé.

  6. Tester aussi la méthode predecessors avec :

    graphe.predecessors('E')

exercice de renforcement

Matrice d'adjacence d'un graphe

On a déjà vu qu'il est possible d'implémenter un graphe à l'aide d'une liste de listes d'adjacence. Une seconde implémentation est possible : avec une matrice d'adjacence. Voici un exemple introductif.

Exemple introductif

Un journaliste britannique d’une revue consacrée à l’automobile doit tester les autoroutes françaises. Pour remplir sa mission, il décide de louer une voiture et de circuler entre six grandes villes françaises : Bordeaux ($B$),Lyon ($L$), Marseille ($M$), Nantes ($N$), Paris ($P$) et Toulouse($T$). Le réseau autoroutier reliant ces six villes est modélisé par le graphe ci-dessous sur lequel les sommets représentent les villes et les arêtes les liaisons autoroutières entre ces villes.

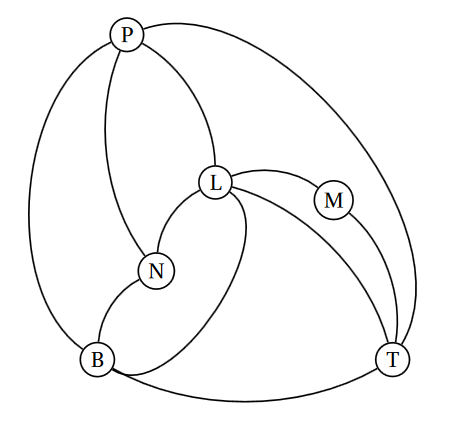
bac ES Polynésie juin 2018

Plutôt que de représenter la situation par un graphe, le journaliste visualise le réseau avec un tableau dans lequel il met 1 s'il existe une liaison directe entre les deux villes correspondant à la case et 0 sinon. Il obtient donc le tableau ci-dessous :

Villes $B$ $L$ $M$ $N$ $P$ $T$
$B$ 0 1 0 1 1 1
$L$ 1 0 1 1 1 1
$M$ 0 1 0 0 0 1
$N$ 1 1 0 0 1 0
$P$ 1 1 0 1 0 1
$T$ 1 1 1 0 1 0

Par exemple, il existe une autoroute reliant directement Paris $P$ à Nantes $N$, donc il y a le nombre 1 dans les cases repérées par $N$ et $P$ ; il n'existe pas d'autoroute reliant directement Marseille $M$ à Bordeaux $B$, donc il y a le nombre 0 dans les cases repérées par $M$ et $B$.

Pour synthétiser l'information (en mémorisant le fait que les villes sont rangées dans l'ordre alphabétique), il suffit de considérer le tableau extrait contenant les données chiffrées. On peut appeler ce tableau matrice. Voici la matrice représentant la situation :

$$G = \begin{pmatrix} 0 &1 &0 &1 &1 &1 \\ 1 &0 &1 &1 &1 &1\\ 0 &1 &0 &0 &0 &1\\ 1 &1 &0 &0 &1 &0 \\ 1 &1 &0 &1 &0 &1\\ 1 &1 &1 &0 &1 &0 \end{pmatrix} $$

Définition

La matrice associée à un graphe d'ordre $n$ est la matrice carrée de taille $n$, où le terme de la $i$-ème ligne et de la $j$-ème colonne est égal au nombre d'arêtes (ou d'arc) partant du sommet $i$ pour arriver au sommet $j$.

Cette matrice s'appelle la matrice d'adjacence de ce graphe.

Un graphe orienté a aussi une matrice d'adjacence.

Le graphe ci-dessous représente, dans un aéroport donné, toutes les voies empruntées par les avions au roulage. Ces voies, sur lesquelles circulent les avions avant ou après atterrissage, sont appelées taxiways. Les sommets du graphe sont les intersections. Les arcs du graphe représentent les voies de circulation (les « taxiways ») en prenant en compte le sens de circulation pour les avions dans les différentes voies ainsi que le temps de parcours pour chacune en minute(s).

bac ES Polynésie juin 2014

Ici, on ne prend pas en compte ici les distances, mais seulement l'existence ou non d'un arc partant d'un sommet et aboutissant à un autre.

Dans la matrice d'adjacence pour un graphe orienté :

Pour simplifier, les sommets sont rangés par ordre croissant, on a donc :

départ = ligne ; arrivée par colonne

Ainsi, on a par exemple :

Ainsi, la matrice $M$ d'adjacence du graphe de cet exemple est

$$M = \begin{pmatrix} 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix}$$

Le graphe suivant représente le plan d’une ville. Les arcs du graphe représentent ses avenues commerçantes, en prenant en compte le sens de circulation, et les sommets du graphe les carrefours de ces avenues.

bac ES métropole septembre 2007

  1. Écrire la matrice $M$ associée à ce graphe. (On rangera les sommets dans l’ordre alphabétique).

  2. Cette matrice est-elle symétrique (par rapport à la diagonale descendante) ? Pourquoi ceci était-il prévisible ?

Code de déblocage de la correction :

exercice de renforcement

D'un graphe vers matrice en langage Python.

On reprend l'exercice précédent :

Le graphe suivant représente le plan d’une ville. Les arcs du graphe représentent ses avenues commerçantes, en prenant en compte le sens de circulation, et les sommets du graphe les carrefours de ces avenues.

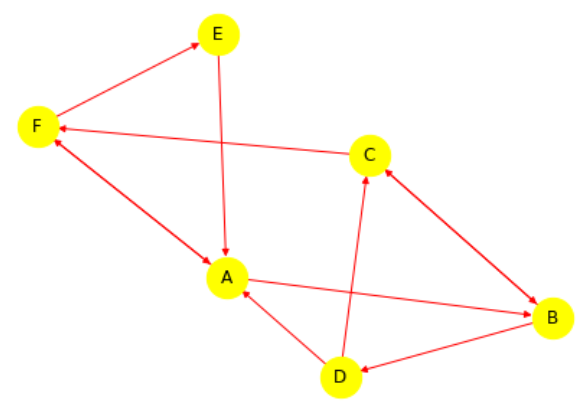
bac ES métropole septembre 2007

  1. En vous aidant du travail déjà effectué lors de l' exercice 10, implémenter en Python le graphe orienté ci-dessus.

  2. Voici un programme à rajouter à la suite du programme précédent ; l'objectif est que la matrice M corresponde à la fin à la matrice d'adjacence du graphe :

    liste = ['A', 'B', 'C', 'D', 'E', 'F']
n = len(liste)
M = [[0]*n for i in range(n)]
for i in range(n):
    for j in range(n):
        ...................... 
            M[i][j] = 1

    1. Que permet la ligne M = [[0]*n for i in range(n)] ?

    2. compléter le programme en remplaçant la ligne ............... par un script qui permet d'avoir la matrice d'adjacence stockée dans M.

    3. Le module networkx contient aussi une fonction permettant d'obtenir la matrice d'adjacence : adjacency_matrix.

    Cependant, Le type de données de cette matrice obtenue avec M = adjacency_matrix(graphe) peut être vu comme une sorte de dictionnaire de dictionnaires, où la clé est un couple de nombres, nombres correspondant à des deux sommets définissant un arc et où la valeur correspond au nombre d'arcs reliant ces deux sommets.

    Or, les nombres des couples des clés ne correspondent pas forcément aux mêmes sommets lors de deux exécutions identiques.

    Ainsi, nous n'utiliserons pas cette méthode ensemble.

exercice de renforcement

Dans cet exercice, vous allez construire un graphe à partir d'une matrice d'adjacence.

Une matrice, étant une sorte de tableau à deux dimensions, peut être implémentée en langage Python sous la forme d'une liste de listes.

On considère la matrice d'adjacence suivante :

$$\begin{pmatrix} 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix}$$

  1. Implémenter cette matrice en exécutant le code suivant

    import networkx as nx  #import de cette bibliothèque gérant les graphes
# importer aussi la bibliothèque suivante afin de représentaer graphiquement le graphe :
import matplotlib.pyplot as plt  

# matrice d'adjacence :
M = [[0, 1, 1, 0, 0, 0, 0, 0],
     [0, 0, 0, 1, 1, 0, 0, 0],
     [0, 1, 0, 1, 0, 0, 0, 0],
     [1, 0, 0, 0, 1, 1, 0, 0],
     [0, 0, 0, 0, 0, 1, 1, 0],
     [0, 0, 0, 0, 0, 0, 1, 1],
     [0, 1, 0, 0, 1, 1, 0, 0],
     [1, 0, 1, 0, 0, 0, 1, 0]]

  2. Cette matrice représente les liens d'amitié dans un réseau social de 8 personnes : Ada, Bryan, Carla, Duc, Elie, Felix, Grace, Hector. (l'ordre alphabétique permet de retrouver l'ordre d'apparition dans la matrice d'adjacence .)

    Explications :
    Le fait que M[0][1]=1 signifie Qu'Ada considère Bryan comme un ami ; le fait que M[2][0]=0 signifie que Carla ne considère pas Ada comme un amie .

    Proposer une fonction creer_graphe qui prend en paramètre une matrice d'adjacence et une liste de noms et qui renvoie le graphe associé à cette matrice.

  3. Tester la fonction avec la matrice précédente.

  4. Représenter graphiquement le graphe du réseau social des 8 personnes mentionnées ci-dessous dont est donnée la matrice d'adjacence.

    N'hésitez pas à reprendre une partie des codes déjà utilisés afin de gérer le tracé.

    Vous devez obtenir un graphique proche de celui-ci :

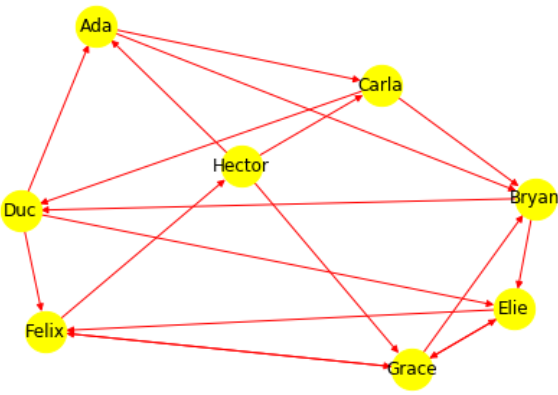
    résultat en image

Code de déblocage de la correction :

exercice de renforcement

Que préférer comme implémentation ?

Nous avons vu qu'il est possible d'implémenter un graphe :

Que préférer ?

Cela dépend de :

  1. la structure du graphe : plus un graphe est "dense", c'est-à-dire plus il y a d'arêtes (ou d'arcs) pour un nombre donnés de sommets, plus la matrice d'adjacence est pertinente.

    En effet, supposons que un graphe avec $n$ sommets et $m$ arêtes :

    • la complexité en mémoire d'une matrice d'adjacence est en $O(n^2)$.

    • la complexité en mémoire d'une liste de listes d'adjacence est en $O(n+m)$.

  2. le travail à faire sur ce graphe : vous verrez dans un prochain chapitre des algorithmes pour étudier et travailler avec des graphes. Certains algorithmes nécessiteront d'implémenter le graphe d'une manière plutôt qu'une autre.

    Dès maintenant, vous pouvez comprendre que pour un graphe à $n$ sommets :

    • si on veut tester que deux sommets sont adjacents ou non :

      on a une complexité en temps en $O(1)$ pour une matrice d'adjacence (lecture directe d'un terme de la matrice)

      mais en $O(d)$ pour une liste d'adjacence où $d$ correspond au degré d'un sommet testé (on doit, dans le cas où il n'y a pas d'arête reliant les sommets, balayer toute la liste des sommets voisins)

      L'implémentation sous forme de matrice d'adjacence est préférable alors.

    • si on veut itérer sur les voisins d'un sommet :

      on a une complexité en temps en $O(n)$ pour une matrice d'adjacence (lecture de tous les termes d'un même ligne (ou colonne) pour connaître quels sont les sommets voisins)

      mais en $O(d)$ pour une liste d'adjacence où $d$ correspond au degré d'un sommet testé (on doit balayer toute la liste des sommets voisins)

      L'implémentation sous forme de liste d'adjacence est préférable alors.

Justifier les complexités en mémoire énoncées au 1. ci-dessus.

Graphe pondéré

Dans de nombreux problème concret, il peut être utile de rajouter une information chiffrée au niveau des arcs ou des arêtes d'un graphe.

Reprenons l'exemple historique des ponts de Königsberg.

Nous avons vu dans l'exemple introductif historique que le problème concret peut être modélisé par le graphe suivant :

modélisation Köenigsberg

On peut modifier ce graphe en ne prenant en compte que le nombre de trajets simples permet de relier deux lieux, on a alors :

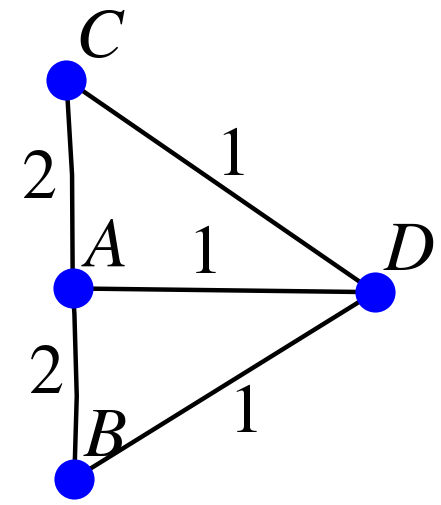
modélisation nombre de trajets avec poids

À ce graphe pondéré, on peut associer la matrice suivante :

$$\begin{pmatrix} 0 & 2 & 2 & 1 \\ 2 & 0 & 0 & 1 \\ 2 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ \end{pmatrix}$$

On peut modifier le graphe en prenant en compte la distance la plus courte pour relier deux lieux correspondant à des sommets adjacents (le 0 signifiant ici que l'arête n'existe pas). On a alors :

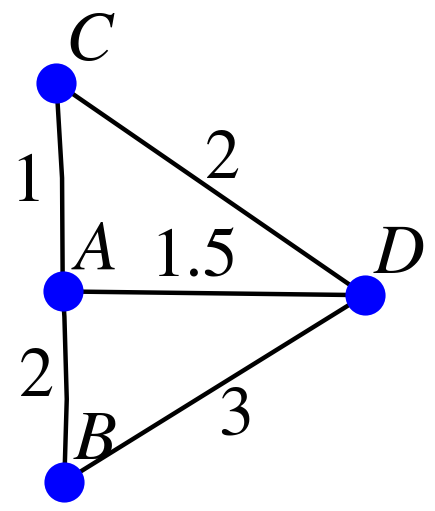
modélisation distance la plis courte avec poids

À ce graphe pondéré, on peut associer la matrice suivante :

$$\begin{pmatrix} 0 & 2 & 1 & 1.5 \\ 2 & 0 & 0 & 3 \\ 2 & 0 & 0 & 2 \\ 1.5 & 3 & 2 & 0 \\ \end{pmatrix}$$

On peut modifier le graphe en prenant en compte le temps minimum , en minutes, pour relier deux lieux correspondant à des sommets adjacents (le 0 signifiant ici que l'arête n'existe pas). On a alors :

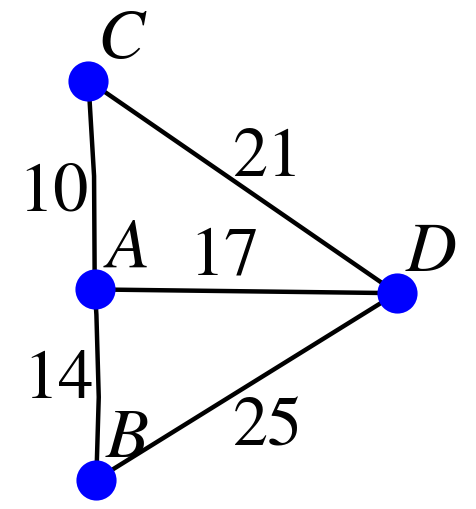
modélisation temps minimum avec poids

À ce dernier graphe pondéré, on peut associer la matrice suivante :

$$\begin{pmatrix} 0 & 14 & 10 & 17 \\ 14 & 0 & 0 & 25 \\ 10 & 0 & 0 & 21 \\ 17 & 25 & 21 & 0 \\ \end{pmatrix}$$

Dans le chapitre sur les algorithmes sur les graphes, l'absence d'un arc entre deux sommets pourra conduire pour certains algorithmes à mettre comme coefficient $\infty$ plutôt que 0.

On appelle graphe pondéré tout graphe dans lequel chaque arête (ou arc) est affectée d'un nombre réel positif appelé poids de cette arête (ou de cet arc).

Le graphe ci-dessous représente, dans un aéroport donné, toutes les voies empruntées par les avions au roulage. Ces voies, sur lesquelles circulent les avions avant ou après atterrissage, sont appelées taxiways. Les sommets du graphe sont les intersections. Les arcs du graphe représentent les voies de circulation (les « taxiways ») en prenant en compte le sens de circulation pour les avions dans les différentes voies ainsi que le temps de parcours pour chacune en minute(s).

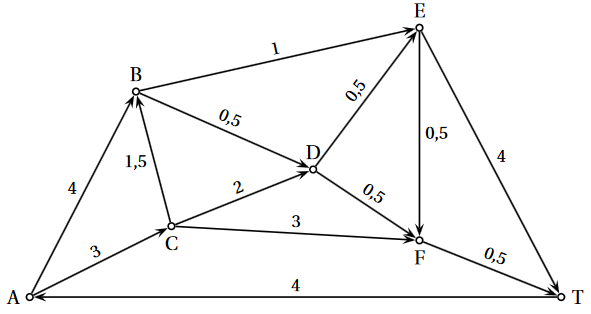
bac ES Polynésie juin 2014

  1. En rangeant les sommets par ordre alphabétique, déterminer la matrice associée à ce graphe orienté pondéré.

  2. Implémenter cette matrice en Python en tant que tableau de tableau.

Code de déblocage de la correction :

exercice de renforcement

On considère un réseau électrique reliant 5 villes appelées "Lorin", "Magis", "Nolin", "Outa" et "Permi".

Les distances du réseau électrique reliant ces villes est donné par la matrice d'adjance suivante :

$$\begin{pmatrix} 0 & 30& 0 & 35 & 0 \\ 30 & 0 & 97 & 0 & 45 \\ 0 & 97 & 0 & 51 & 59 \\ 35 & 0 & 51 & 0 & 40 \\ 0 & 45 & 59 & 40 & 0 \\ \end{pmatrix}$$

L'objectif est de pouvoir implémenter le graphe pondéré associé à ce type de matrice d'adjacence où les termes sont les poids.

  1. Proposer une fonction matrice_vers_liste qui :

    • prend comme premier paramètre matrice une matrice d'adjacence de type d'un tableau de tableaux, matrice qui contient les poids du graphe pondéré,

    • prend comme second paramètre noms une liste de chaînes de caractères qui correspond aux noms des sommets, sommets appraissant dans l'ordre de la matrice,

    • renvoie un dictionnaire dont les clés sont les sommets et les valeurs sont une liste de tuples au format ("nom_sommet",poids)

  2. Utiliser cette fonction matrice_vers_liste pour créer le graphe pondéré associé à la matrice d'adjacence donnée au début de l'exercice.

    La méthode add_weighted_edges_from de networkx permet d'ajouter un arc pondéré au graphe sur lequel s'applique cette méthode.

  3. Obtenir une représentation graphique de ce graphe.

    Afin d'avoir des sommets régulièrement disposés autour d'un cercle et d'afficher chaque arête avec son poids, il suffit de finir votre script par : 

    # pour la visualisation d'un graphe pondéré :
# position des sommets régulièrement répartis autour d'un cercle :
position_sommets=nx.circular_layout(g)
# affichage des étiquettes de poids :
etiquettes = dict([((u, v), d['weight'])
                 for u, v, d in g.edges(data=True)])   
# tracé du graphe avec les étiquettes de poids :
nx.draw(g, position_sommets, node_size=800, node_color="yellow", edge_color="red", with_labels=True)
nx.draw_networkx_edge_labels(g, position_sommets, edge_labels=etiquettes, label_pos=0.5)
plt.show()

Code de déblocage de la correction :

idée venant de Nathalie Daval : accès au document ayant donné l'idée.

Profitant de vacances, vous partez à la Réunion pour oublier l'informatique.

Mais à peine arrivé.e.s à l'aéroport de Saint-Denis de la Réunion, vous voilà coincé.e.s dans un bouchon.

Par chance, le conducteur vous donne des informations sur le temps pour parcourir le trajets entre différents lieux de la ville.

Grâce aux compétences acquises en NSI, vous avez traduit les informations données par le conducteur par ce graphe pondéré :

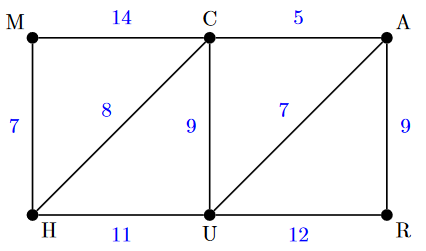
irem.univ-reunion.fr/IMG/pdf/Cours_Graphes.pdf

Dans ce plan, pour simplifier les notations suivantes ont été prises : M correspondant à La Montagne, H pour Hôpital, C pour Cimetière, U pour Université, A pour Aéroport et R pour Rivière des pluies.

  1. Implémenter le graphe pondéré sous forme d'un dictionnaire où les clés sont les sommets et les valeurs sont une liste de tuples au format ("sommets",temps)

  2. Proposer une fonction dict_vers_matrice qui :

    • prend comme paramètre graphe un dictionnaire où les clés sont les sommets et les valeurs sont une liste de tuples au format ("sommets",temps),

    • renvoie un tuple constitué de la matrice d'adjacence associée au graphe pondéré et de la liste des sommets du graphe.

Code de déblocage de la correction :

On repère sur une carte 12 lieux précis, lieux sur lesquels on affecte une lettre de reconnaissance, on détermine les liaisons possibles, on détermine les coordonnées, on représente alors l'ensemble sous forme d'un graphe.

  1. Que contient la variable etiquettes à l'issue de l'exécution du script suivant ?

    etiquettes = [chr(ord('A') + i) for i in range(12)]

    2. Dans la suite de l'exercice, chaque sommet du graphe portera une etiquette qui sera lié à un numéro de sorte que si le sommet du numéro $k$ aura pour étiquette etiquettes[k].

    Dans cet exercice, on représente le graphe lié à ces sommets par une liste de listes d’adjacences list_adj telle que list_adj[k] est la liste des sommets voisins du sommet k.

  2. On admet que la liste de listes d'adjacences est donnée ici par : 

    list_adj = [[1, 6], [0, 2, 3], [1, 3, 9], [1, 2, 4], [3, 5], [4, 11], [0, 7, 8], 
                            [6, 8], [6, 7, 9, 10], [2, 8, 10, 11], [8, 9, 11], [5, 9, 10]]

    En observant la liste précédente, à quel(s) sommet(s) le sommet $D$ est-il lié ?

  3. On admet que les coordonnées de chaque sommet du graphe sont données par la liste de tuples suivant : 

    coord = [(0, 2), (0, 3), (1, 2), (2, 3), (2, 4), (4, 4), (0, 1), 
                        (1, 0), (2, 0), (3, 2), (4, 1), (4, 3)]

    Quelles sont les coordonnées du sommet $F$ ?

  4. Écrire une fonction dist_eucli qui prend en paramètres deux couples de deux coordonnées et qui renvoie la distance euclidienne entre les deux points repérés par ces coordonnées (dans un repère orthonormé) sous forme de flottant.

    • Penser à utiliser le module math,

    • Rappel sur le calcul de la distance euclidienne :
      si $A(x_A;y_A)$ $B(x_B;y_B)$ alors la distance euclidienne entre les deux points $A$ et $B$ est donnée par : $$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$$

    • Penser à utiliser des préconditions pour s'assurer que les deux paramètres sont des tuples à deux éléments.

    • Penser à tester cette fonction.

  5. On veut désormais obtenir une représentation visuelle de ce graphe en utilisant le module matplotlib.pyplot importé sous l'alias plt.

    1. importer correctement ce module dans le script déjà créé.

    2. Voici un script à rajouter à la suite du script déjà obtenu :

      for i in range(12):
    plt.text(coord[i][0], coord[i][1], etiquettes[i], size=25)
    plt.plot(coord[i][0], coord[i][1],  marker = 'o', markerfacecolor = 'blue', markersize = 8)
    for j in list_adj[i] :
        print(j)
        plt.plot([coord[i][0], coord[j][0]], [coord[i][1],coord[j][1]], 'r-', lw=2) 
        plt.text((coord[i][0]+coord[j][0])/2, (coord[i][1]+coord[j][1])/2, round(dist_eucli(coord[i], coord[j]), 3), size=10)
plt.show()

      Rajouter ce script et le commenter en utilisant si besoin les documentations suivantes :

    3. En exécutant le script complet, vous devez voir apparaître une figure proche de celle-ci :

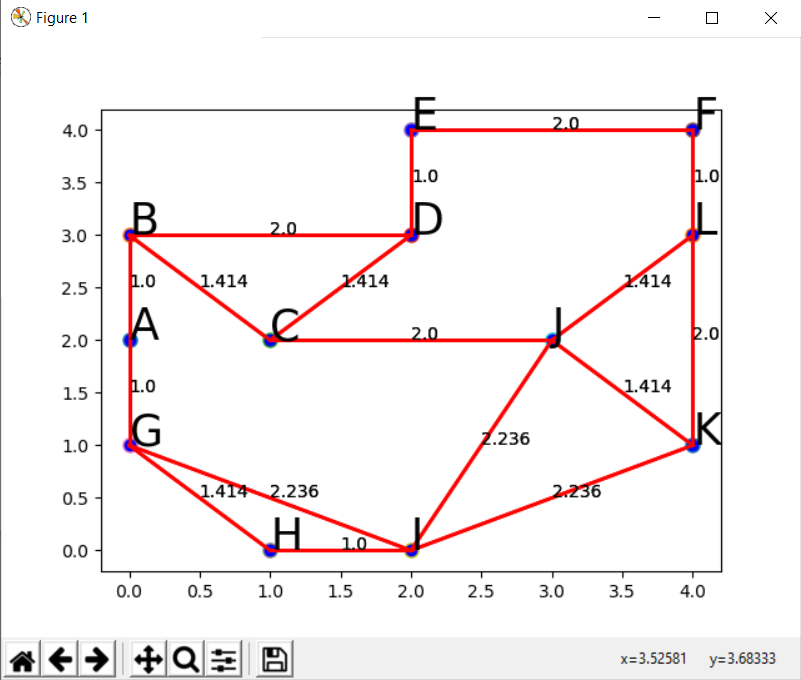
      figure à obtenir

      Vérifiez-le.

exercice de renforcement

Pour revoir une explication complète sur les graphes et le vocabulaire, vous vouvez visionner la vidéo accessible ici.

Modélisation d'un graphe à l'aide de la programmation objet

Le but est d'implémenter un graphe sous forme d'un dictionnaire où :

  1. Créer une classe nommé Graphes et la documenter rapidement.

    2. Code de déblocage de la correction :

  2. L'attribut caché __graphe contiendra les données d'un graphe sous forme d'un dictionnaire.

    Créer le constructeur __init__(self, graphe={}) qui permet de créer soit un graphe vide par défaut, soit un graphe initialisé avec le graphe saisi comme deuxième paramètre.

    3. Code de déblocage de la correction :

  3. Rajouter la méthode suivante à votre classe ; cette méthode permettra d'afficher une représentation de l'objet sur lequel s'appliquera cette méthode. 

       def __repr__(self):
    """
    permet d'afficher une représentation du graphe objet (sous forme de dictionnaire).
    """
    return repr(self.__graphe)  #utilisation de la fonction native repr qui permet ceci.

  4. Créer la méthode ajouter_sommet qui prend en paramètre sommet de type chaîne de caractères. cette méthode doit rajouter ce sommet comme clé du dictionnaire graphe sur lequel s'applique cette méthode si cette clé n'était pas présente dans le dictionnaire.
    Attention ! Ici, on ne rajoute que le sommet, donc la valeur de la clé rajoutée est par défaut une liste vide !

    5. Code de déblocage de la correction :

  5. Créer la méthode ajouter_arc prend en paramètres :

    • sommet_origine, la clé correspondant au sommet d'origine de l'arc, de type chaîne de caractères,

    • sommet_cible, chaine de caractères correspondant au sommet de l'extrémité de l'arc,

    • poids, flottant correspondant au poids de l'arc ; par défaut, ce poids vaut 1.

    Cette méthode doit rajouter :

    • rajouter au dictionnaire graphe sur lequel s'applique cette méthode, les sommets donnés en paramètres qui ne figureraient pas encore comme clé,

    • rajouter à la clé sommet_origine comme valeur le tuple (sommet_cible,poids).

    6. Code de déblocage de la correction :

  6. Tester le code déjà fait en mettant en tout fin de programme le test suivant :

    if __name__ == "__main__":
    # Point d'entrée en exécution.
    graph = Graphes()
    graph.ajouter_sommet("A")
    graph.ajouter_sommet("B")
    graph.ajouter_sommet("C")
    graph.ajouter_sommet("D")
    graph.ajouter_sommet("E")
    graph.ajouter_sommet("F")

    graph.ajouter_arc("A", "C", 5)
    graph.ajouter_arc("A", "E", 1)
    graph.ajouter_arc("A", "F", 3)
    graph.ajouter_arc("B", "A", 2)
    graph.ajouter_arc("B", "D", 5)
    graph.ajouter_arc("C", "A", 4)
    graph.ajouter_arc("D", "A", 5)
    graph.ajouter_arc("D", "C", 1)
    graph.ajouter_arc("D", "F", 3)
    graph.ajouter_arc("E", "D", 2)
    graph.ajouter_arc("E", "F", 9)
    graph.ajouter_arc("F", "B", 7)

    print("graphe initial")
    print(graph.__repr__())

    Lors le l'exécution du code vous devez voir apparaître, à l'ordre près des facteurs :

    graphe initial
{'C': [('A', 4)], 'F': [('B', 7)], 'E': [('D', 2), ('F', 9)], 'A': [('C', 5), ('E', 1), ('F', 3)], 'D': [('A', 5), ('C', 1), ('F', 3)], 'B': [('A', 2), ('D', 5)]}

  7. Voici ci-dessous une méthode myst :

    def myst(self, sommet_origine, sommet_cible):
        
        temp = self.__graphe[sommet_origine].copy()   # liste des valeurs de la clé sommet_origine
        n= len(temp)
        for elt in temp:                              # balayage de tous les valeurs de la liste : attention  tuple ("nom", poids)
            if sommet_cible == elt[0]:
                self.__graphe[sommet_origine].remove(elt)

    Déterminer le rôle de cette méthode puis changer son nom myst en un nom explicitant son rôle.

    8. Code de déblocage de la correction :

  8. Proposer le destructeur suivant : une méthode enlever_sommet qui prend en paramètres :

    • sommet, chaine de caractères correspondant au sommet à supprimer,

    • sommet_cible, chaine de caractères correspondant au sommet de l'extrémité de l'arc.

    méthode qui supprime le sommet saisi ainsi que toutes les valeurs associées à ce sommet dans le dictionnaire représentant le graphe.

    Attention ! Cette méthode doit aussi enlever les tuple où le sommet à supprimer apparaît et ce pour pour toutes les clés.

    9. Code de déblocage de la correction :

  9. Tester le code déjà fait en mettant désormais en tout fin de programme le test suivant :

    if __name__ == "__main__":
    # Point d'entrée en exécution.
    graph = Graphes()
    graph.ajouter_sommet("A")
    graph.ajouter_sommet("B")
    graph.ajouter_sommet("C")
    graph.ajouter_sommet("D")
    graph.ajouter_sommet("E")
    graph.ajouter_sommet("F")

    graph.ajouter_arc("A", "C", 5)
    graph.ajouter_arc("A", "E", 1)
    graph.ajouter_arc("A", "F", 3)
    graph.ajouter_arc("B", "A", 2)
    graph.ajouter_arc("B", "D", 5)
    graph.ajouter_arc("C", "A", 4)
    graph.ajouter_arc("D", "A", 5)
    graph.ajouter_arc("D", "C", 1)
    graph.ajouter_arc("D", "F", 3)
    graph.ajouter_arc("E", "D", 2)
    graph.ajouter_arc("E", "F", 9)
    graph.ajouter_arc("F", "B", 7)

    print("graphe initial")
    print(graph.__repr__())
    print("graphe sans C")
    graph.enlever_sommet("C")
    graph.__repr__()

    Lors le l'exécution du code vous devez voir apparaître, à l'ordre près des facteurs :

    graphe initial
{'A': [('C', 5), ('E', 1), ('F', 3)], 'B': [('A', 2), ('D', 5)], 'C': [('A', 4)], 'D': [('A', 5), ('C', 1), ('F', 3)], 'E': [('D', 2), ('F', 9)], 'F': [('B', 7)]}
graphe sans C
{'A': [('E', 1), ('F', 3)], 'B': [('A', 2), ('D', 5)], 'D': [('A', 5), ('F', 3)], 'E': [('D', 2), ('F', 9)], 'F': [('B', 7)]}

  10. Proposer une méthode get_matrice qui :

    1. commence par créer la liste des sommets l_sommets du graphe, liste qui sera triée par ordre croissant.

    2. crée la matrice d'adjacence où les sommets sont rangés par ordre croissant et dont les termes correspondent au poids de l'arc éventuel partant du sommet lié à la ligne et pointant vers le sommet lié à la colonne, avec la convention de mettre 0 si un tel arc n'existe pas.

    3. renvoie la matrice d'adjacence associée au graphe sur lequel s'applique la méthode sous forme de liste de listes.

    11. Code de déblocage de la correction :

  11. Tester le code déjà fait en mettant désormais en tout fin de programme le test suivant :

    if __name__ == "__main__":
    # Point d'entrée en exécution.
    graph = Graphes()
    graph.ajouter_sommet("A")
    graph.ajouter_sommet("B")
    graph.ajouter_sommet("C")
    graph.ajouter_sommet("D")
    graph.ajouter_sommet("E")
    graph.ajouter_sommet("F")

    graph.ajouter_arc("A", "C", 5)
    graph.ajouter_arc("A", "E", 1)
    graph.ajouter_arc("A", "F", 3)
    graph.ajouter_arc("B", "A", 2)
    graph.ajouter_arc("B", "D", 5)
    graph.ajouter_arc("C", "A", 4)
    graph.ajouter_arc("D", "A", 5)
    graph.ajouter_arc("D", "C", 1)
    graph.ajouter_arc("D", "F", 3)
    graph.ajouter_arc("E", "D", 2)
    graph.ajouter_arc("E", "F", 9)
    graph.ajouter_arc("F", "B", 7)

    print("graphe initial")
    print(graph.__repr__())
    print(graph.get_matrice())
    print("graphe sans C")
    graph.enlever_sommet("C")
    graph.__repr__()
    print(graph.get_matrice())

    Lors le l'exécution du code vous devez voir apparaître, à l'ordre près des facteurs :

    graphe initial
{'A': [('C', 5), ('E', 1), ('F', 3)], 'B': [('A', 2), ('D', 5)], 'C': [('A', 4)], 'D': [('A', 5), ('C', 1), ('F', 3)], 'E': [('D', 2), ('F', 9)], 'F': [('B', 7)]}
[[0, 0, 5, 0, 1, 3], [2, 0, 0, 5, 0, 0], [4, 0, 0, 0, 0, 0], [5, 0, 1, 0, 0, 3], [0, 0, 0, 2, 0, 9], [0, 7, 0, 0, 0, 0]]
graphe sans C
{'A': [('E', 1), ('F', 3)], 'B': [('A', 2), ('D', 5)], 'D': [('A', 5), ('F', 3)], 'E': [('D', 2), ('F', 9)], 'F': [('B', 7)]}
[[0, 0, 0, 1, 3], [2, 0, 5, 0, 0], [5, 0, 0, 0, 3], [0, 0, 2, 0, 9], [0, 7, 0, 0, 0]]

Exercices de renforcement

Graphe non-orienté

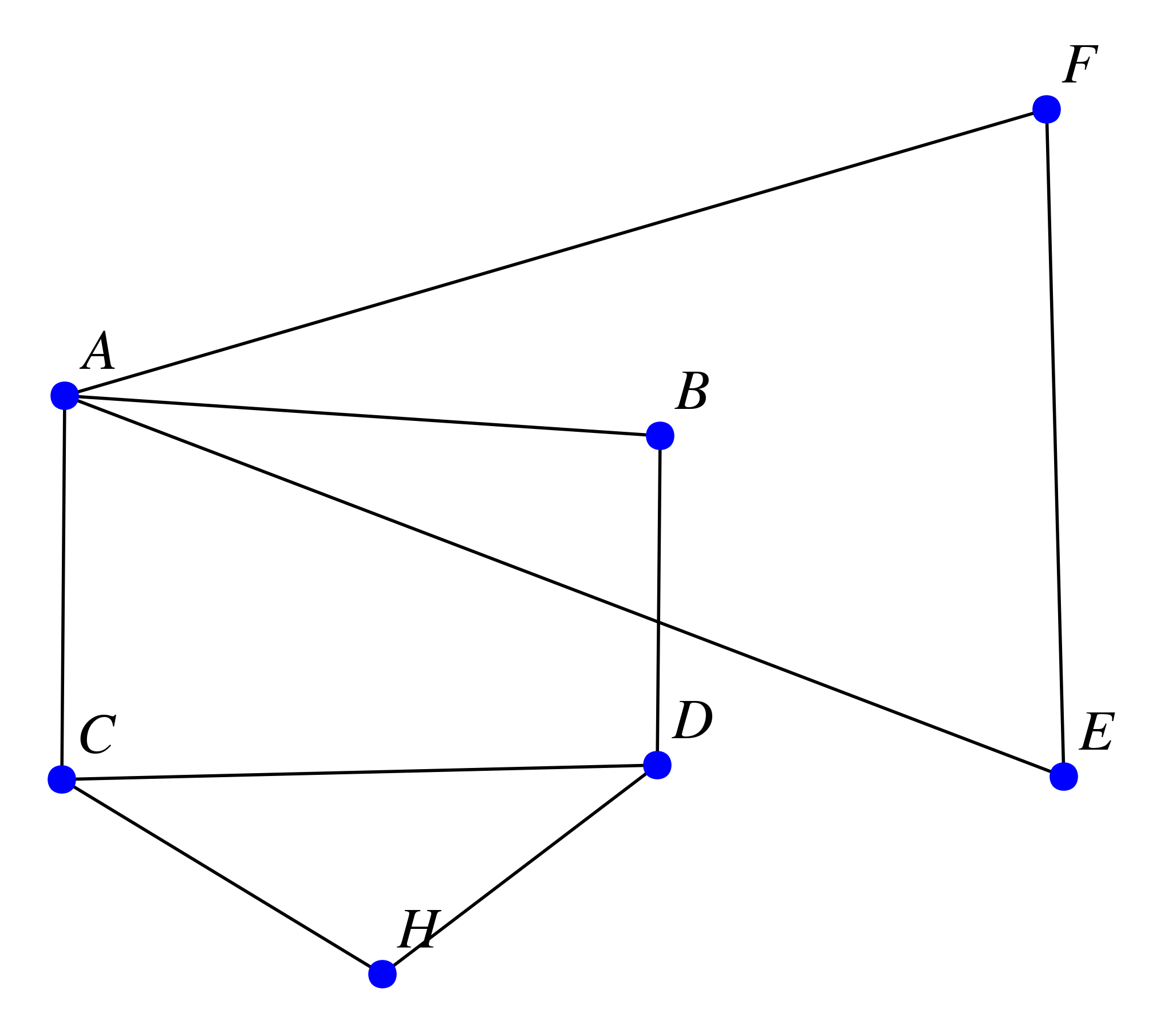
On considère le graphe représenté ci-dessous ; il modélise le plan d'un village. Les arêtes du graphe représentent ses rues et les sommets les croisements de celle-ci.

graphe exo renf 1

  1. Quel est l'ordre du graphe ?

  2. Déterminer le degré de chacun des sommets.

  3. Quel est le nombre de rues de ce village ?

  4. Citer deux sommets adjacents.

  5. Citer deux sommets non adjacents.

  6. Ce graphe est-il complet ?

Cliquer pour afficher la solution

  1. Le graphe est d'ordre 7.

  2. Sommet

    		 A B C D E F H
    Ordre 4 2 3 3 2 2 2

  3. Il y a 9 rues dans ce village puisqu'il y a 9 arêtes dans ce graphe.

  4. B et D sont des sommets adjacents.

  5. C et B sont des sommets non adjacents.

  6. Le graphe n'est pas un graphe complet car deux sommets au moins ne sont pas adjacents.


  1. Écrire une fonction degre qui prend en paramètre un dictionnaire ainsi qu'un sommet sous forme de chaîne de caractères et qui renvoie le degré de ce sommet entré comme paramètre.

  2. Tester la fonction degre.

  3. Proposer des préconditions.

  4. Proposer une fonction nombre_aretes qui prend en paramètre un dictionnaire implémentant un graphe non orienté et qui renvoie le nombre d'arêtes de ce graphe graphe.

Cliquer pour afficher la solution

1.

def degre(graphe: dict, sommet: str) -> int:
    """
    graphe est un dictionnaire associant à chaque sommet sa liste de sommets adjacents.
    sommet est le nom d'un des sommets du graphe.
    Renvoie le degré du sommet entré comme deuxième argument dans le graphe.
    """
    return len(graphe[sommet])

2.

graphe = {}   # création d'un dictionnaire vide 
graphe["A"] = ["B", "C", "E", "F", "H"] # liens de A vers les sommets listés
graphe["B"] = ["A", "D", "H"]
graphe["C"] = ["A", "F",  "G", "H"]
graphe["D"] = ["B", "H"]
graphe["E"] = ["A", "H"]
graphe["F"] = ["A", "C"]
graphe["G"] = ["C", "H"]
graphe["H"] = ["A", "B", "C", "D", "E", "G"]
print(degre(graphe, "A"))

renvoie bien 5.

3.

def degre(graphe: dict, sommet: str) -> int:
    """
    graphe est un dictionnaire associant à chaque sommet sa liste de sommets adjacents.
    sommet est le nom d'un des sommets du graphe.
    Renvoie le degré du sommet entré comme deuxième argument dans le graphe.
    """
    assert type(graphe) is dict
    assert type(sommet) is str
    return len(graphe[sommet])

4.

def nombre_aretes(graphe: dict) -> int:
    """
    graphe est un dictionnaire associant à chaque sommet sa liste de sommets adjacents.
    On suppose que le graphe est non orienté.
    Renvoie le nombre d'arêtes du graphe (arêtes : graphe non orienté !)
    """
    nb = 0
    for valeur in graphe.values():
        nb += len(valeur)
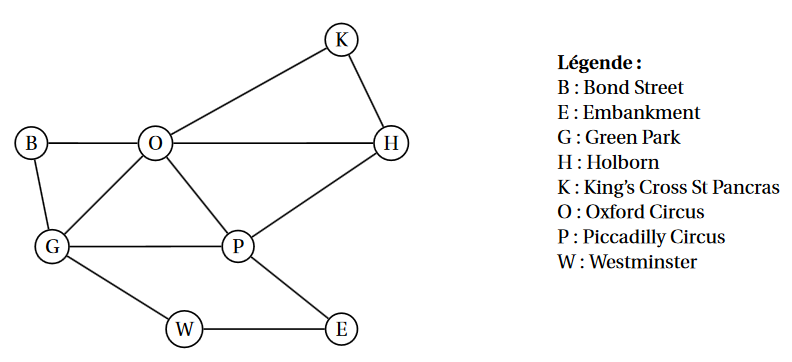
    return nb//2     # chaque arête est comptée deux fois : une pour chaque sommet

On a schématisé ci-dessous une partie du plan du métro londonien par un graphe $\Gamma$ dont les sommets sont les stations et les arêtes sont les lignes desservant ces stations.

Chaque station de métro est désignée par son initiale comme indiqué dans la légende.

Bas ES centre étranger juin 2015

  1. Quel est l'ordre du graphe ?

  2. Proposer un cycle qui permettrait de passer par chacune des stations de métro du graphe $\Gamma$.

  3. Déterminer en justifiant si le graphe $\Gamma$ est connexe.

  4. Proposer une chaine de longueur 6 reliant $H$ à $P$.

  5. Déterminer un cycle de longueur 10 .

  6. On appelle chaîne eulérienne une chaîne qui permet de passer par toutes les arêtes une et une seule fois.

    Existe-t-il une chaîne eulérienne à ce graphe $\Gamma$ ? Si oui, en donner une.

Cliquer pour afficher la solution

  1. Le graphe est d'ordre 8 car il y a 8 sommets.

  2. Voici un cycle qui permet de passer par chacune des stations de métro du graphe $\Gamma$ : $O-B-G-W-E-P-H-K$.

  3. Le graphe $\Gamma$ est connexe car tout sommet est relié à tout autre sommet par une succession d'arêtes (=chaîne).

  4. Voici une chaîne de longueur 6 reliant $H$ à $P$ : $H-K-O-G-W-E-P$.

  5. Voici un cycle de longueur 10 : $O-H-P-E-W-G-O-P-G-B-O$.

  6. On appelle chaîne eulérienne une chaîne qui permet de passer par toutes les arêtes une et une seule fois.

    Il existe une chaîne eulérienne à ce graphe $\Gamma$ : $H-K-O-H-P-E-W-G-O-P-G-B-O$.


Graphe orienté

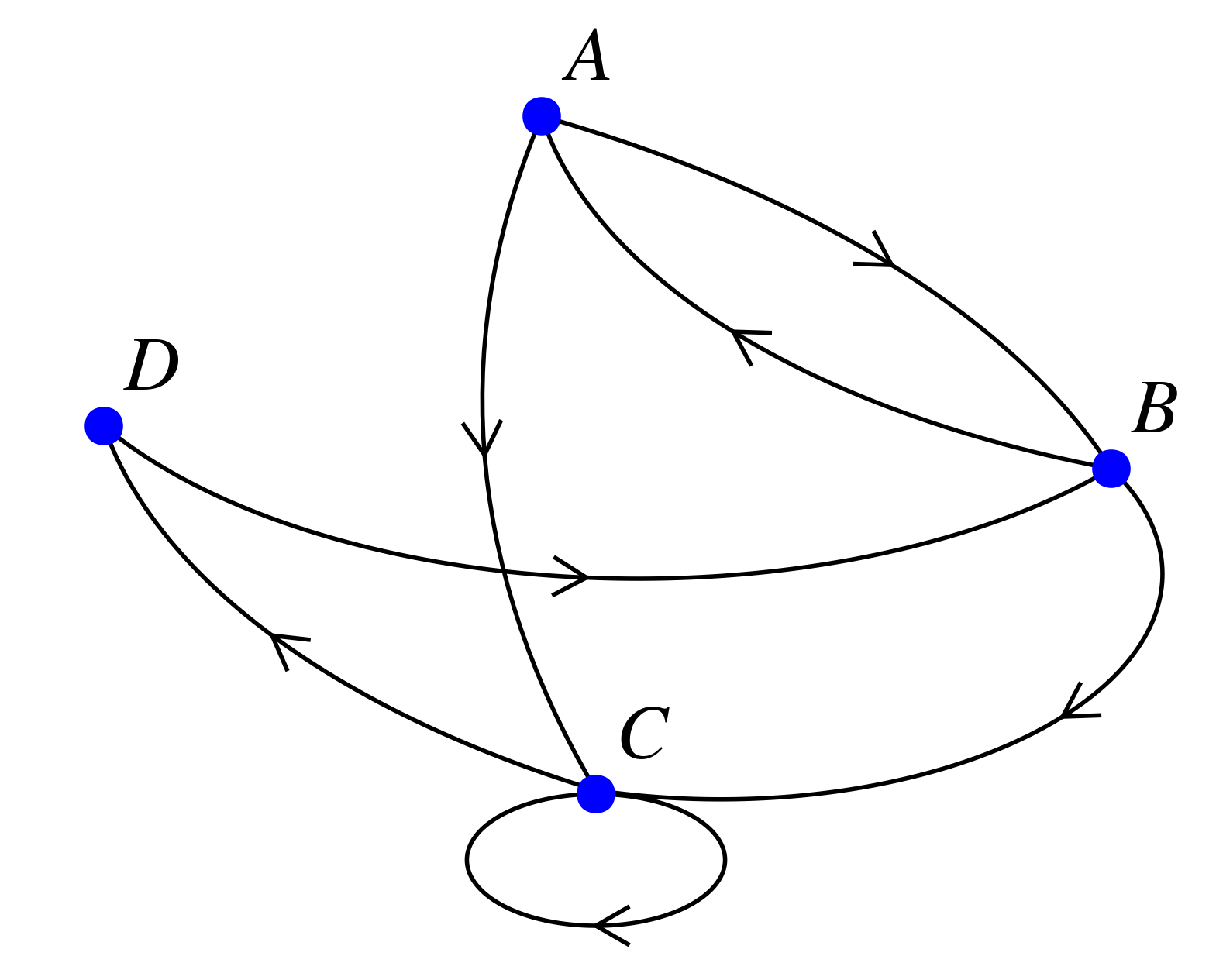
Voici un graphe :

exo renf graphe orienté du cours

  1. Est-ce un graphe orienté ou non-orienté ? Pourquoi ?

  2. Quel est l'ordre du graphe ?

  3. Existe-t-il un circuit passant par $D$ de longueur 2 ?

  4. Existe-t-il un circuit passant par $C$ de longueur 1 ?

  5. Proposer un chemin de longueur 6 passant par tous les sommets.

Cliquer pour afficher la solution

  1. C'est un graphe orienté car l'arc entre $A$ et $C$ permet d'aller directement de $A$ à $C$ mais le sens inverse n'est pas possible directement.

  2. Le graphe est d'ordre puisqu'il y a sommets.

  3. Il n'existe pas de circuit passant par $D$ de longueur 2 car pour arriver à $D$, il faut nécessairement venir de $C$ et de plus, de $D$, on ne peut aller que vers $B$.
    Ainsi, tout circuit passant par $D$ passe aussi par $B$ et par $C$ : la longueur dépasse donc forcément 2.

  4. Il existe un circuit passant par $C$ de longueur 1 : le circuit $C->C$

  5. Voici un chemin de longueur 6 passant par tous les sommets : $A->B->A->C->C->D->B$.


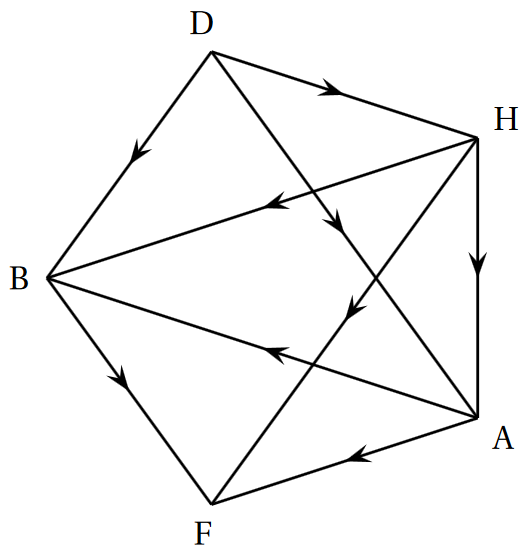
Un parcours sportif est composé d'un banc pour abdominaux, de haies et d'anneaux. Le graphe orienté ci-dessous indique les différents parcours conseillés partant de D et terminant à F.

Les sommets sont: D (départ), B (banc pour abdominaux), H (haies), A (anneaux) et F (fin du parcours).

Les arcs représentent les différents sentiers reliant les sommets.

Voici un graphe orienté modélisant les parcours :

bac ES métropole juin 2018

En utilisant les méthodes du module networkx, réaliser successivement les tâches suivantes permettant d'implémenter puis de visualiser le graphe associé au parcours.

  1. Créer un graphe orienté vide.

  2. Ajouter au graphe chacun des sommets.

  3. Ajouter au graphe chacun des arcs.

  4. Visualiser le graphe grâce à la bibliothèque matplotlib.pyplot afin de vérifer votre code.

Cliquer pour afficher la solution 
import networkx as nx  #import de cette bibliothèque gérant les graphes
import matplotlib.pyplot as plt

#1. Création du graphe vide
graphe = nx.DiGraph()  

#2. Ajout des sommets
liste_sommets = ["A", "B", "D", "F", "H"]  
for elt in liste_sommets:
    graphe.add_node(elt)

#3. Ajout des arcs
graphe.add_edges_from([("A", "B"), ("A", "F")])            # arcs issus du sommet A
graphe.add_edges_from([("B", "F")])  
graphe.add_edges_from([("D", "A"), ("D", "B"), ("D", "H")]) 
graphe.add_edges_from([("H", "B"), ("H", "F")])  

#4. tracé 
options = {
            'node_size' : 800,   # taille des sommets
            'node_color' : 'blue', # couleur de fond des sommets
            'edge_color' : 'red', # couleur des arcs
            'with_labels' : 'True',  # avec le nom des sommets
          }
nx.draw(graphe, **options)
plt.show()

Le but est d'étudier le grphe de l'exercice précédent :

bac ES métropole juin 2018

Utiliser les méthodes et fonctions du module networkx pour :

  1. obtenir le degré du sommet 'H' du graphe.

  2. obtenir le nombre de sommets de ce graphe.

  3. obtenir le nombre d'arcs de ce graphe.

  4. obtenir la liste des sommets voisins au sommet 'A' de ce graphe.

  5. obtenir la liste des sommets successeurs du sommet 'A' de ce graphe.

  6. obtenir la liste des sommets prédécesseurs du sommet 'A' de ce graphe.

Cliquer pour afficher la solution 
import networkx as nx  

# implémentation du graphe issue de l'exercice précédent
graphe = nx.DiGraph()  

liste_sommets = ["A", "B", "D", "F", "H"]  
for elt in liste_sommets:
    graphe.add_node(elt)

graphe.add_edges_from([("A", "B"), ("A", "F")])            # arcs issus du sommet A
graphe.add_edges_from([("B", "F")])  
graphe.add_edges_from([("D", "A"), ("D", "B"), ("D", "H")]) 
graphe.add_edges_from([("H", "B"), ("H", "F")])  

#1. degré :
print("degré de H :", graphe.degree('H'))
#2. nombre de sommets :
print("nombre de sommets :", graphe.number_of_nodes())
#3. nombre d'arcs :
print("nombre d'arcs :", graphe.number_of_edges())
#4. nombre des voisins de 'A'
print("voisins de 'A' :", list(graphe.neighbors('A')))   # Attention à transtyper l'itérateur obtenu avec la méthode neighbors en une liste
#5. successeurs de 'A'
print("successeurs de 'A' :", list(graphe.successors('A')))
#6. prédecessseurs de 'A'
print("prédécesseurs de 'A' :", list(graphe.predecessors('A')))

matrice d'adjacence

Un parcours sportif est composé d'un banc pour abdominaux, de haies et d'anneaux. Le graphe orienté ci-dessous indique les différents parcours conseillés partant de D et terminant à F.

Les sommets sont: D (départ), B (banc pour abdominaux), H (haies), A (anneaux) et F (fin du parcours).

Les arcs représentent les différents sentiers reliant les sommets.

bac ES métropole juin 2018

  1. Écrire à la main la matrice d'adjacence $M$ associée à ce graphe. (On rangera les sommets dans l’ordre alphabétique).

  2. Cette matrice est-elle symétrique (par rapport à la diagonale descendante) ? Pourquoi ceci était-il prévisible ?

  3. Comment se traduit sur la matrice d'adjacence le fait qu'aucun arc ne permet d'atteindre le sommet $D$ ?

Cliquer pour afficher la solution

  1. Voici la matrice d'adjacence $M$ associée à ce graphe : $$M = \begin{pmatrix} 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 \\ \end{pmatrix}$$

  2. Cette matrice n'est pas symétrique par rapport à la diagonale descendante car le graphe est non orienté.

  3. Sur la matrice d'adjacence le fait que tous les termes de la troisième colonne, celle correspondant à $D$, sont nuls traduit le fait qu'aucun arc ne permet d'atteindre le sommet $D$.


Un parcours sportif est composé d'un banc pour abdominaux, de haies et d'anneaux. Le graphe orienté ci-dessous indique les différents parcours conseillés partant de D et terminant à F.

Les sommets sont: D (départ), B (banc pour abdominaux), H (haies), A (anneaux) et F (fin du parcours).

Les arcs représentent les différents sentiers reliant les sommets.

bac ES métropole juin 2018

  1. En vous aidant du travail déjà effectué lors de l'exercice de renforcement accessible ici, implémenter en Python le graphe orienté ci-dessus.

  2. Proposer une fonction creer_mat_adj qui reçoit comme paramètre un graphe de type dictionnaire et renvoie la matrice d'adjacence associée à ce graphe (de type à ne pas préciser).

  3. Vérifier la fonction creer_mat_adj avec le graphe ci-dessus.

Cliquer pour afficher la solution

1. et 2.

#1. implémentation du graphe sous forme d'un dictionnaire associant à chaque sommet sa liste de sommets adjacents.
graphe = {}
graphe["A"] = ["B", "F"]
graphe["B"] = ["F"]
graphe["D"] = ["A", "B", "H"]
graphe["H"] = ["A", "B", "F"]

#2. fonction créant la matrice d'adjacence :
def creer_mat_adj(graphe:dict):
    """
    graphe est un graphe implémenté sous forme d'un dictionnaire associant à chaque sommet sa liste de sommets adjacents.
    Fonction qui renvoie la matrice d'adjacence associée au graphe (où les sommets sont rangés dans l'ordre alphabétique)
    """
    sommets = list(graphe.keys())
    # rajout des sommets n'étant l'origine d'aucun arc (comme "F") :
    for deb in graphe.keys():  # Attention à ne pas écrire 'in sommets' car la liste sommets peut être modifiée au cours du balayage
        for fin in graphe[deb]:
            if fin not in sommets:
                sommets.append(fin)
    # tri des sommets par ordre alphabétique :
    sommets.sort()
    # création de la matrice d'adjacence :
    mat = []
    for i in range(len(sommets)):
        ligne = []
        for j in range(len(sommets)):
            if sommets[i] in graphe.keys() and sommets[j] in graphe[sommets[i]] : # ordre important
                ligne.append(1)
            else:
                ligne.append(0)
        mat.append(ligne)
    return mat

3. La fonction creer_mat_adj renvoie pour le graphe ci-dessus implémenté la liste [[0, 1, 0, 1, 0], [0, 0, 0, 1, 0], [1, 1, 0, 0, 1], [0, 0, 0, 0, 0], [1, 1, 0, 1, 0]].
Cette liste correspond bien à la matrice d'adjacence du graphe obtenue à l'exercice de renforcement précédent : $$M = \begin{pmatrix} 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 \\ \end{pmatrix}$$


On considère un parcours de formation reliant différents pôles nommés pour simplifier $A$, $B$, $C$, $D$, $E$ et $F$.

La matrice d'adjacence $N$ associée au graphe représentant le parcours de formation, dans lequel les sommets sont classés en ordre alphabétique, est :

$$N = \begin{pmatrix} 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ \end{pmatrix}$$

  1. Implémenter en Python la matrice ci-dessus.

  2. Représenter graphiquement le graphe du parcours de formation dont est donnée la matrice d'adjacence est donnée ci-dessus.

Cliquer pour afficher la solution

1. Voici une implémentation de la matrice d'adjacence : 

N = [[0, 1, 0, 1, 0, 1],
     [0, 0, 1, 1, 0, 1],
     [1, 1, 0, 0, 1, 0],
     [0, 0, 0, 0, 0, 0],
     [1, 1, 0, 0, 0, 1],
     [1, 0, 0, 1, 0, 0]]

2. Voici une représentation possible du graphe associé à cette matrice d'adjacence :


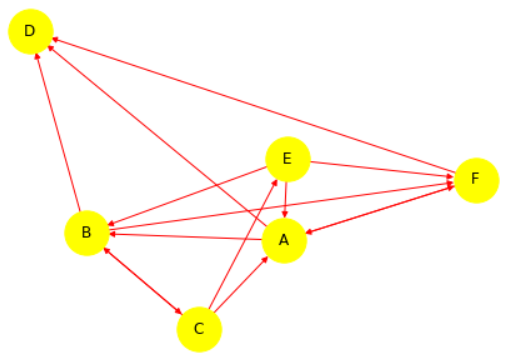
Graphe pondéré

Le graphe ci-dessous représente le réseau routier d'un centre-ville qui prend en compte le sens de circulation, chaque arc représente une voie à sens unique dont le poids est la distance le temps moyen nécessaire entre deux sommets.

bac ES doc accompagenment 2002

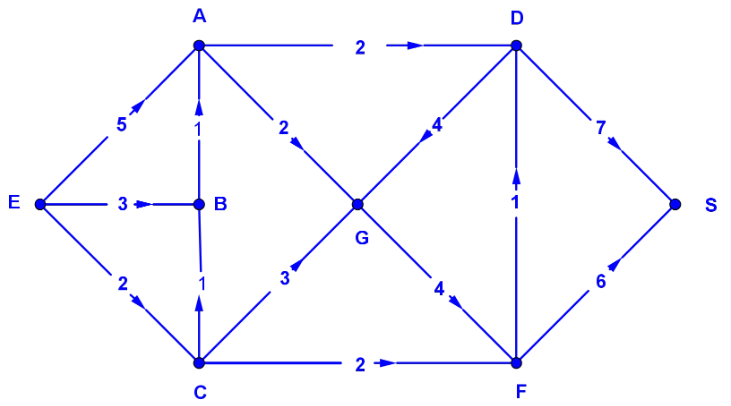
  1. En rangeant les sommets par ordre alphabétique, déterminer la matrice associée à ce graphe orienté pondéré.

  2. Implémenter cette matrice en Python en tant que tableau de tableau.

Cliquer pour afficher la solution

1. Voici la matrice associée à ce graphe pondéré orienté : $$M = \begin{pmatrix}0& 0& 0& 2& 0& 0& 2& 0\\ 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 2& 3& 0\\ 0& 0& 0& 0& 0& 0& 4& 7\\ 5& 3& 2& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 6\\ 0& 0& 0& 0& 0& 4& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ \end{pmatrix}$$

2. Voici une implémentation cette matrice : 

M = [[0, 0, 0, 2, 0, 0, 2, 0], 
     [1, 0, 0, 0, 0, 0, 0, 0], 
     [0, 1, 0, 0, 0, 2, 3, 0], 
     [0, 0, 0, 0, 0, 0, 4, 7], 
     [5, 3, 2, 0, 0, 0, 0, 0], 
     [0, 0, 0, 1, 0, 0, 0, 6], 
     [0, 0, 0, 0, 0, 4, 0, 0], 
     [0, 0, 0, 0, 0, 0, 0, 0]]

Le but est d'obtenir grâce à matplotlib.pyplot une figure représentant le graphe ci-dessous :

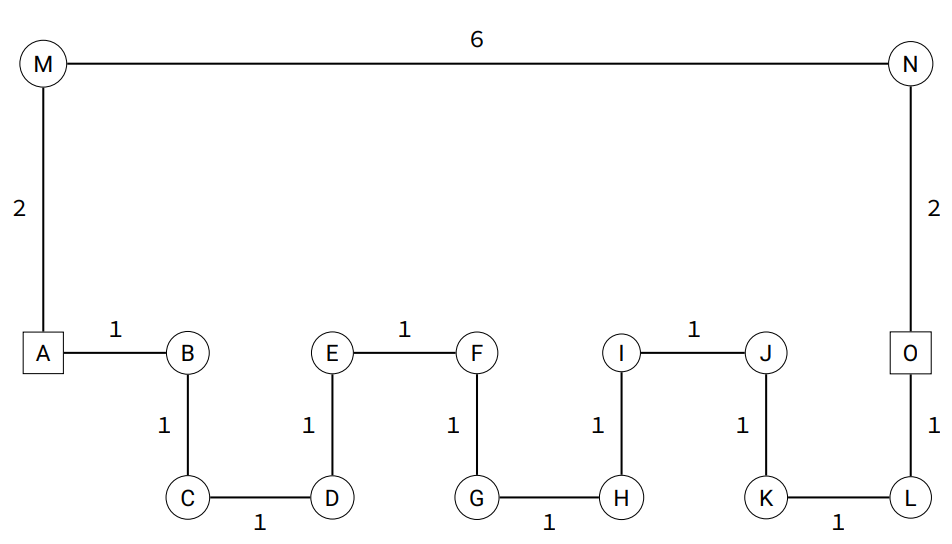
issu du document d'accompagnement : RA20_NSI_G_T_plus-court-chemin_1307008 ; page 4

  1. Proposer une ligne de code permettant de stocker dans une variable liste_noms la liste des noms des points en faisant en sorte de pouvoir identifier rapidement un nom de point avec son index.

  2. Sachant que le point $A$ a pour coordonnées $(1,0)$, que $B(1;1)$ et que $N(6;3)$, créer un variable coord, liste des tuples correspondant aux coordonnées des points, les points apparaissant dans le même ordre que dans liste_noms.

  3. On admet que la liste d'adjacence est donnée par la liste adj suivante : 

    adj = [[1, 12], [0, 2], [1, 3], [2, 4], [3, 5], [4, 6], [5, 7], [6, 8],
                            [7, 9], [8, 10], [9, 11], [10, 14], [0, 13], [12, 14], [11, 13]]

    En vous aidant de la fin de l'exercice accessible ici, finalisez votre script afin qu'il permette de faire apparaître le graphe pondéré associé à la liste d'adjacence et où le poids de chaque arête correspond à la distance euclidienne entre les deux sommets reliés.

Cliquer pour afficher la solution

Voici un script solution possible : 

import matplotlib.pyplot as plt
from math import sqrt

# 1. création de la liste des noms des points :
liste_noms = [chr(ord('A') + i) for i in range(15)]

# 2. création de la liste des coordonnées des points :
coord = [(0 , 1), (1, 1), (1, 0), (2, 0), (2, 1), (3, 1), (3, 0), (4, 0), (4, 1),
        (5, 1), (5, 0), (6, 0), (0, 3), (6, 3), (6, 1)]

# 3. fin de l'exercice :
adj = [[1, 12], [0, 2], [1, 3], [2, 4], [3, 5], [4, 6], [5, 7], [6, 8],
        [7, 9], [8, 10], [9, 11], [10, 14], [0, 13], [12, 14], [11, 13]]

def dist_eucli(P1: tuple, P2: tuple) -> float:
    """
    P1 et P2 sont deux couples de coordonnées correspondant à deux points du plan
    renovie la distance euclidienne entre les deux points repérés par ces coordonnées
    """
    assert type(P1) == tuple and len(P1)==2, "P1 doit coorespondre à un couple de coordonnées"
    assert type(P2) == tuple and len(P2)==2, "P1 doit coorespondre à un couple de coordonnées"
    return sqrt((P1[0]-P2[0])**2+(P1[1]-P2[1])**2)

for i in range(15):
    plt.text(coord[i][0], coord[i][1], liste_noms[i], size=25)
    plt.plot(coord[i][0], coord[i][1], marker = 'o', markerfacecolor = 'blue', markersize = 8)
    for j in adj[i] :
        plt.plot([coord[i][0], coord[j][0]], [coord[i][1], coord[j][1]], 'r-', lw=2) # Red straight line
        plt.text((coord[i][0]+coord[j][0])/2, (coord[i][1]+coord[j][1])/2, round(dist_eucli(coord[i], coord[j]), 3), size=10)

plt.show()

Savoirs et savoirs-faire

  1. le vocabulaire sur les graphes non-orientés (ordre, sommets adjacents, degré, chaîne, longueur, connexe, complet),

  2. le vocabulaire sur les graphes orientés (arc, degré),

  3. connaître la notion de graphe pondéré.

  4. la notion de matrice d'adjacence.

  1. modéliser un problème concret à l'aide d'un graphe,

  2. écrire la mtrice d'adjacence associée à un graphe.

  3. implémenter en Python un graphe.

  4. implémenter en Python une matrice (d'adjacence )

  5. savoir utiliser les méthodes essentielles du module networkx pour étudier un graphe.

Sitographie

Voici quelques liens:


Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲