- Liste - Dictionnaire
- Récursivité
- sd1 : interface, pile, file
- sd2 : POO
- BDD : base de données
- sd4 : arbres
- sd5 : graphe
- arse2 : ordonnancement
- a2 : Algorithme sur les graphes
- a3 : Diviser pour régner
Cette page est dédiée aux exercices de début de séances : des exercices ciblés, assez courts, visant à installer des automatismes.
Vous retrouvez l'équivalent en première dans la section avant propos : Warmup - Automatismes .
Cette page est utile pour vous préparer à l'exercice 1 de l'épreuve pratique du baccalauréat. A travailler et retravailler sans modération.
Bon codage à vous !
- Le ou les thème(s) : par exemple
pile,récursivité, etc . - Une indication : par exemple la fonction avec son nom.
- Une indication du type : papier (pour un format sans ordinateur) , à compléter (exercice à trous).
Pour faciliter vos recherches, en entrée de challenge vous avez :
Liste - Dictionnaire
if while balayage liste dictionnaire algorithmes
Répondre aux six questions suivantes qui reprennent différents éléments vus en premières sur le langage Python et en algorithmie.
Penser à vérifier chaque réponse.
Ne pas hésiter à appeler en cas de question, de doute ou d'incompréhension.
dico_lettres(phrase) dictionnaire type str
Écrire une fonction dico_lettres(phrase) qui prend une variable typée str phrase en argument et renvoie le dictionnaire des occurrences des lettres de phrase.
Par exemple, dico_lettres('bob') renvoie {'b': 2, 'o': 1} .
Écrire une fonction est_trie_croissant(l) qui prend une variable typée list l en argument
et renvoie un booléen qui indique si la liste est triée.
Par exemple, est_trie_croissant([1, 2, 3]) renvoie True .
Par exemple, est_trie_croissant([]) renvoie True .
Par exemple, est_trie_croissant([2, 1, 3, 4]) renvoie False .
Vous pouvez compliquer votre code en traitant les cas où les nombres sont dans l'ordre croissant ou décroissant.
Dictionnaire, tuple
Baston! Partie 1
On dispose d'un dictionnaire constitué de chaînes de caractères pour clés représentant le nom de personnages et de tuple constituant les valeurs. Les tuples sont constitués de trois entiers : le premier qui représente l'initiative du personnage, le second l'attaque du personnage et le dernier la défense.
characters ={'Conan' : (5, 123, 25), 'Galadriel' : (5, 60, 60), 'Rey' : (6, 100,25), 'Bob l’éponge' : (1, 12, 12), 'Passe kal T rez' : (12, 1200, 1200)} -
Écrire une fonction
firstAttack(characters, character1, character2)qui prend en argument un dictionnaire du type décrit ci-dessus et deux chaînes de caractères qui renvoie le personnage avec le plus d'initiative. -
Ajouter une précondition afin de vérifier que character1 et character2 sont dans le dictionnaire characters.
-
Bonus : proposer d'autres personnages pour nourrir le dictionnaire et rendre la suite plus distrayante.
Dictionnaire, liste, papier
Baston! Partie 2
On dispose d'un dictionnaire constitué de chaînes de caractères pour clés représentant le nom de personnages et de tuple constituant les valeurs. Les listes sont constitués de trois entiers : le premier qui représente l'initiative du personnage, le second l'attaque du personnage et le dernier la défense.
characters ={'Conan' : [5, 123, 25], 'Galadriel' : [5, 60, 60], 'Rey' : [6, 100,25], 'Bob l’éponge' : [1, 12, 12], 'Passe kal T rez' : [12, 1200, 1200]} -
Écrire une fonction
battle(characters, character1, character2)qui prend en arguments un dictionnaire du type décrit ci-dessus et deux chaînes de caractères qui modifie le dictionnaire conséquemment au combat. Le personnage avec plus d'initiative frappe en premier, si le second survie, il frappe à son tour. La fonction renverra l'état des deux combatants. Dans cette question, l'attaque agit sur la défense du personnage attaqué.En cas d'égalité d'initiative, les deux attaques portent.
-
Bonus : proposer d'autres personnages pour nourrir le dictionnaire et rendre la suite plus distrayante.
chaîne de caractères
Écrire une fonction supp_lettre(phrase, car) qui prend en arguments phrase et car
qui sont de type str
Cette fonction renvoie phrase dans laquelle car a été supprimé.
Liste des tests :
assert supp_lettre("élémentaire", "e") == "élémntair"
assert supp_lettre("", "i") == "" Chaîne de caractères, dictionnaires
Écrire une fonction dico_lettre(phrase) qui prend en argument phrase
qui est de type str
Cette fonction renvoie un dictionnaire dont les clés sont les caractères de phrase
et les valeurs les occurrences de ces caractères.
Liste des tests :
assert dico_lettre("Hello world !") == {'H': 1, 'e': 1, 'l': 3, 'o': 2, ' ': 2, 'w': 1, 'r': 1, 'd': 1, '!': 1}
assert dico_lettre("") == {} Liste, tuple, balayage
Un ensemble de relevés de températures est stocké dans une liste releves.
Cette liste est composés de tuples de la forme ("nom_ville",temperature) où temperature est un nombre
entier ou flottant.
Proposer une fonction temp_moyenne qui prend en paramètre une telle liste ainsi que le nom d'une ville et qui renvoie
la moyenne des températures présentent dans la liste associées à cette ville ou 0 si le nom de la ville n'apparaît pas.
Voici un jeu de tests :
assert temp_moyenne([("Paris",12),("Reims",13),("Paris",14),("Paris",19)],"Paris") == 15.0
assert temp_moyenne([("Paris",12),("Reims",13),("Paris",14),("Paris",19)],"Reims") == 13.0
assert temp_moyenne([("Paris",12),("Reims",13),("Paris",14),("Paris",19)],"Troyes") == 0dictionnaire, tuple, balayage, maximum
Des collectionneurs de carte à jouer ont chacun relevé l'ensemble de leurs cartes dans un dictionnaire dont les clés sont le nom des personnages des cartes et les valeurs associées sont des tuples formés du type de carte (str) et de l'effectif de cartes possédées dans la collection.
Par exemple, un joueur a relevé ses quelques cartes ainsi :
dicoJoueurE = {"Elfica": ("Elfe", 2),"Jean": ("humain", 3), "Lam": ("Elfe", 1)}-
Proposer une fonction
effectifqui prend en paramètre un tel dictionnaire ainsi que le nom d'une carte et qui renvoie le nombre de cartes portant ce nom dans la collection considérée.
Par exemples :
effectif(dicoJoueurE, "Jean")renvoie 3.
effectif(dicoJoueurE, "Neymar")renvoie 0. -
-
Quelle ligne de code en python suffit d'écrire ici pour balayer tout le dictionnaire pour pouvoir étudier chaque type ?
-
Proposer une fonction
compter_typequi prend en paramètre un tel dictionnaire et le nom d'un type de cartes et qui renvoie le nombre cumulé de cartes de ce type dans la collection considérée.
Par exemples :
compter_type(dicoJoueurE,"Elfe")renvoie 3.
compter_type(dicoJoueurE,"Nain")renvoie 0.
Ces collectionneurs veulent connaître le nombre total de cartes d'un type donné possédées.
-
Dictionnaire, liste, maximum, liste par compréhension, proche épreuve pratique
Une entreprise veut améliorer ses produits.
Pour cela, elle vous demande d'étudier un ensemble de pièces produites
qui risquent d'être défectueuses pour construire un dictionnaire qui associera
à chaque type de défaut le nombre de pièces présentant se défaut.
Ensuite, vous devrez donner à l'entreprise le type de défaut le plus fréquent.
Les types de défaut peuvent être classés entre 3 catégories : "A",
"B" et "C". La catégorie "O" signifie que la pièce ne présente
pas de défaut.
Voici deux exemples de liste donnant les catégories des pièces étudiées :
pieces1 = ["O", "B", "A", "A", "C", "O", "A", "B", "B", "C", "O", "A"]
pieces2 = ["O", "C", "C", "O", "A", "B", "O", "O", "A"]
La fonction categoriser doit permettre de compter le nombre de pièces rencontrées de chaque catégorie.
Elle prend en paramètre un tableau formé d'éléments "O", "A", "B" ou "C" et renvoie le résultat dans un
dictionnaire dont les clés sont les noms des catégories trouvées et les valeurs le nombre de pièces de cette catégorie.
La fonction defaut_max doit désigner le nom du ou des catégories liées à un défaut la plus fréquente observée.
Elle prend en paramètre un dictionnaire dont la structure est celle du dictionnaire renvoyé par la
fonction categoriser et renvoie un tableau.
Ce tableau peut donc contenir plusieurs catégories s’il y a des types de défaut aussi fréquents.
Compléter les fonctions categoriser et defaut_max suivantes :
def categoriser(pieces: list) -> dict:
resultat = ...
for piece in pieces:
if ...:
resultat[piece] = resultat[piece] + 1
else:
...
return resultat
def defaut_max(result_etude: dict) -> list:
nom_defaut = ""
nb_max = 0
for defaut in result_etude:
if defaut ... and ... > ...:
nom_defaut = defaut
nb_max = ...
liste_finale = [categorie for categorie in result_etude if categorie ... and result_etude[categorie] == ...]
return liste_finaleVous pouvez tester les fonctions complétées à l'aide de ce jeu de tests :
>>> resul1 = categoriser(pieces1)
>>> resul1
{'O': 3, 'B': 3, 'A': 4, 'C': 2}
>>> defaut_max(resul1)
['A']
>>> resul2 = categoriser(pieces2)
>>> resul2
{'O': 4, 'C': 2, 'A': 2, 'B': 1}
>>> defaut_max(resul2)
['C', 'A']
Un trail est une course à pied en milieu naturel.
Une trace (ou trace GPS) est une liste d’au moins deux positions géographiques
représentant un parcours.
Dans cet exercice, on souhaite réaliser des programmes de trails à partir de leur trace.
La trace d’une course est stockée dans un fichier au format CSV (Comma Separated Values).
Chaque ligne du fichier
contient, dans cet ordre, la latitude en degrés Nord, la longitude en degrés Est (tous
deux des nombres à virgule) puis l’altitude en mètres, et enfin une valeur d’horodatage
ou timestamp (tous deux des entiers).
Les valeurs des horodatages (timestamps) sont des valeurs en secondes, exprimées à partir d’une date référence (1ᵉʳ janvier 1970). La différence entre deux horodatages donne donc le temps écoulé entre les deux mesures en secondes.
Dans cet exercice, on considère un trail tout proche du lac des Vielles Forges dans les Ardennes.
Le fichier est téléchargeable en cliquant ici
et voici les premières lignes de ce fichier avec ses quatre descripteurs :
latitude, longitude, altitude, temps
49.87338, 4.59889, 247, 1764087945
49.87313, 4.59914, 247, 1764087948
49.87302, 4.59968, 247, 1764087951
49.87297, 4.60004, 246, 1764087954
49.87291, 4.60046, 246, 1764087957
La lecture du fichier est effectuée par le programme Python suivant (il n’est pas nécessaire de comprendre ce code pour pouvoir faire cet exercice) :
import csv
def lecture_trace_csv(filename):
"""
Prend une chaîne de caractère (nom du fichier) en entrée
et renvoie une liste contenant les données lues
"""
tab_trace = []
with open(filename, 'r') as f: # ouverture du fichier
csvreader = csv.reader(f, delimiter=',') # lecture du contenu en précisant que le délimiteur du csv est la virgule
for ligne in csvreader: # balayage de l'itérable ; ligne est une liste correspondant à une ligne du fichier csv
tab_trace.append(ligne) # rajout dans la liste à renvoyer
return tab_trace[1:] # renvoi de la liste à partir de la deuxième ligne -
Appliquer cette fonction sur le fichier
lac_vieilles_forges.csvtéléchargé et Vérifier que les premières renvoyées sont :[['49.87338', '4.59889', '247', '1764087945'], ['49.87313', '4.59914', '247', '1764087948'], ['49.87302', '4.59968', '247', '1764087951'], ['49.87297', '4.60004', '246', '1764087954'], ['49.87291', '4.60046', '246', '1764087957'], ... ] -
La variable
tab_traceest donc une liste contenant des listes de quatre chaînes de caractères.
Pour réaliser des calculs sur les données de la trace, il est nécessaire de convertir les différentes valeurs en nombres (floatpour la latitude et la longitude etintpour l’altitude et le temps en format timestamp).Proposer une fonction
creation_trace, prenant en paramètre une liste similaire àtab_traceet renvoyant une liste de dictionnaires, chaque dictionnaire contenant une position horodatée (avec les quatre cléslat,lon,alt,tsp).Le renvoi de cette fonction sur la liste obtenue au 1. doit commencer ainsi :
[{'lat': 49.87338, 'lon': 4.59889, 'alt': 247, 'tsp': 1764087945}, {'lat': 49.87313, 'lon': 4.59914, 'alt': 247, 'tsp': 1764087948}, {'lat': 49.87302, 'lon': 4.59968, 'alt': 247, 'tsp': 1764087951}, {'lat': 49.87297, 'lon': 4.60004, 'alt': 246, 'tsp': 1764087954}, {'lat': 49.87291, 'lon': 4.60046, 'alt': 246, 'tsp': 1764087957}, ...] -
Proposer une fonction
valeurs_altitudequi prend en paramètre une trace en tant que liste de dictionnaire, comme obtenu à la question précédente, et renvoie la liste des altitudes successives. -
Pour demain !
Récursivité
nombre_de_chiffres(n)Écrire une fonction récursive nombre_de_chiffres(n) qui prend un entier positif ou nul n en argument et renvoie son nombre de chiffres.
Par exemple, nombre_de_chiffres(12568) renvoie 5.
Voici les étapes à suivre (ou des rappels) pour réaliser le programme :
-
Trouver la condition d'arrêt en réfléchissant aux cas les plus simples pour lesquels vous connaissez directement le nombre de chiffres qui compose le nombre.
-
Pour le cas général, penser que si vous connaissez le nombre de chiffres qui compose le nombre de dizaines d'un chiffre $n$, vous pouvez en déduire le nombre de chiffres qui compose ce nombre $n$.
-
Le nombre de dizaines d'un entier $n$ peut être obtenu comme le quotient de la division euclidienne de $n$ par 10 avec le script :
n//10. -
Dans le cas général, la fonction récursive
nombre_de_chiffresdoit être utilisée. -
Le nombre de chiffres composant $12568$ est 5, tandis que le nombre de chiffres composant $1256$, le nombre de dizaines, est 4.
-
Tester le bon fonctionnement de la fonction
nombre_de_chiffres.
Copier puis compléter le script suivant en vous servant des commentaires et des tests proposés ci-dessus.
def nombre_de_chiffres(n):
if n < ...:
...
else:
return ... + nombre_de_chiffres(...)Attention ! Il y a d'autres manières d'écrire le script demandé, manières tout aussi pertinentes que celle proposée ci-dessus avec des trous.
est_trie(l) à compléterCompléter les fonctions récursives est_croissant(l) et est_decroissant(l) puis la fonction est_trie(l)qui prend une variable code typée list l en argument
et renvoie un booléen qui indique si la liste est triée.
def est_croissant(l):
if len(l) <= 1:
return ...
elif .... :
l = l[1:]
return ........
else:
return False
def est_decroissant(l):
if len(l) <= 1:
return True
elif l[0] >= l[1]:
l = l[1:]
return .....
else:
return False
def est_trie(l):
if len(l) <= 1:
return .....
elif l[0] <= l[1]:
l = l[1:]
return .....
elif ...:
l = l[1:]
return .....
else:
return .....
# La batterie de tests
def test() :
assert est_croissant([]) == True , 'Erreur test vide'
assert est_croissant([1]) == True , 'Erreur test [1]'
assert est_croissant([1,2]) == True , 'Erreur test [1,2]'
assert est_croissant([1,2,1]) == False , 'Erreur test [1,2,1]'
assert est_decroissant([]) == True , 'Erreur test vide'
assert est_decroissant([1]) == True , 'Erreur test [1]'
assert est_decroissant([1,1]) == True , 'Erreur test [1,1]'
assert est_decroissant([1,2,1]) == False , 'Erreur test [1,2,1]'
assert est_decroissant([13,2,1]) == True , 'Erreur test [13,2,1]'
assert est_trie([]) == True , 'Erreur test vide'
assert est_trie([1]) == True , 'Erreur test [1]'
assert est_trie([1,2]) == True , 'Erreur test [1,2]'
assert est_trie([1,2,1]) == False , 'Erreur test [1,2,1]'
assert est_trie([1,1]) == True , 'Erreur test [1,1]'
assert est_trie([13,2,1]) == True , 'Erreur test [13,2,1]'
test()Tri insertion récursive
-
Écrire une fonction récursive
insertion(lst, x, i)qui insère correctementxdanslstoùiest l'index dex. Au lancement de la fonction les éléments d'index 0 à i-1 delstsont triés.insertion([2, 25, 32, 5, 6, 21], 5, 3)renvoie[2, 5, 25, 32, 6, 21] -
Écrire une fonction récursive
tri_insertion_rec(lst,n)qui renvoie la listelsttriée,n-1est l'indice du dernier terme de la liste.
Un capteur mesure la température à l'intérieur d'un réfrigérateur.
L'ensemble des mesures prises un temps donné par ce capteur est stocké dans une liste.
Pour garantir la sécurité alimentaire des produits stockés, la température doit rester
au maximum en dessous de 5 degrés Celsius.
Proposer une fonction récursive trop_chaud qui
prend en paramètre une liste de flottants et qui renvoie le nombre de réels supérieurs ou
égaux à 5.
Exemples de tests :
assert trop_chaud([]) == 0
assert trop_chaud([-6, 4.9]) == 0
assert trop_chaud([4.8, 5, 5.1, 5.01, 4.98, 4.95, 4.8, 4.8, 4.85, 4.9]) == 3
assert trop_chaud([4,6, 5]) == 2
assert trop_chaud([5, 4.5, 4, 3]) == 1Voici les étapes à suivre (ou des rappels) pour réaliser le programme :
-
Trouver la condition d'arrêt en réfléchissant au cas le plus simple pour une liste.
-
Le premier élément d'une liste
lstest obtenu aveclst[0]. -
Pour le cas général, il y a deux possibilités à traiter suivant si le premier terme est inférieur ou non à 5.
-
Dans le cas général, la fonction récursive
trop_chauddoit être utilisée. -
La liste
lst[1:]est la liste formée des éléments de la listelstsans le premier premier termelst[0]. -
Tester le bon fonctionnement de la fonction
trop_chaud.
Copier puis compléter le script suivant en vous servant des commentaires et des tests proposés ci-dessus.
def trop_chaud(mesures: list) -> int:
"""mesure est une liste de nombres réels.
trop_chaud est une fonction récursive.
Cette fonction renvoie le nombre de réels supérieurs ou égaux à 5"""
if mesures == ...: # cas simple de la condition d'arrêt
return ...
else: # cas général : on regarde le premier élément et on appelle la fonction sur le reste de la liste
if mesures[0] ...:
...
else:
...Attention ! Il y a d'autres manières d'écrire le script demandé, manières tout aussi pertinentes que celle proposée ci-dessus avec des trous.
On considère la fonction maxi qui prend en paramètres des nombres
a et b et qui renvoie le maximum de ces deux nombres :
def maxi(a, b):
if a > b:
return b
else:
return a
Proposer une fonction récursive maximum_liste
qui prend en paramètre une liste non vide de nombres et renvoie le maximum de cette liste.
Exemples de tests :
assert maximum_liste([-3]) == -3
assert maximum_liste([4,-3, 5.6, -7]) == 5.6
assert maximum_liste([9, 8, 7, 6, 5, 4, 3, 2, 1, 0]) == 9
assert maximum_liste([1, 3, 8]) == 8
assert maximum_liste([-2, 6, 3, 4, 6, -5]) == 6Voici les étapes à suivre (ou des rappels) pour réaliser le programme :
-
Trouver la condition d'arrêt en réfléchissant au cas le plus simple pour une liste non vide.
-
Le premier élément d'une liste
lstest obtenu aveclst[0]. -
Pour le cas général, penser que trouver le maximum de toute la liste revient à trouver le plus grand nombre entre le premier élément de la liste et le maximum de la liste réduite aux éléments dont l'indice est supérieur ou égal à 1.
-
Dans le cas général, la fonction
maxide l'énoncé peut être utilisée. -
Dans le cas général, la fonction récursive
maximum_listedoit être utilisée. -
La liste
lst[1:]est la liste formée des éléments de la listelstsans le premier premier termelst[0]. -
Tester le bon fonctionnement de la fonction
maximum_liste.
Copier puis compléter le script suivant en vous servant des commentaires et des tests proposés ci-dessus.
def maxi(a, b):
if a > b:
return b
else:
return a
def maximum_liste(liste: list):
if ...: # cas d'une liste réduite à un seul élément
...
else:
return maxi(..., ...)
# tests :
assert maximum_liste([-3]) == -3
assert maximum_liste([4,-3, 5.6, -7]) == 5.6
assert maximum_liste([9, 8, 7, 6, 5, 4, 3, 2, 1, 0]) == 9
assert maximum_liste([1, 3, 8]) == 8
assert maximum_liste([-2, 6, 3, 4, 6, -5]) == 6Attention ! Il y a d'autres manières d'écrire le script demandé, manières tout aussi pertinentes que celle proposée ci-dessus avec des trous.
Un palindrome est un mot qui se lit de la même manière de la gauche vers la droite que de la
droite vers la gauche.
Par exemple : "a", "kayak", "ressasser" sont des palindromes ; tandis que "ares"
n'en est pas un.
Compléter la fonction récursive est_palindrome ci-dessous
qui prend une chaîne de caractères comme paramètre et qui renvoie le booléen True
si cette chaîne est un palindrome et False sinon.
def est_palindrome(ch):
if ...:
return True
elif ...:
return False
else:
ch = ... # chaîne de caractères sans le premier ni le dernier caractère
...Exemples de tests :
assert est_palindrome("kayak") == True
assert est_palindrome("oui") == False
assert est_palindrome("ESOPERESTEICIETSEREPOSE") == True Voici quelques rappels sur une chaîne de caractères ch :
-
L'expression
len(ch)donne le nombre de caractères de la chaînech. -
L'expression
ch[-1]donne le donne le dernier caractère de la chaînech. -
L'expression
ch[1:-1]donne une chaîne de caractères correspondant à la chaînechprivée de son premier caractère et de son dernier caractère.
Voici les étapes à suivre (ou des rappels) pour réaliser le programme :
-
Trouver les deux conditions d'arrêts en réfléchissant :
-
Quel est le plus simple pour qu'une chaîne de caractères soit un palindrome ?
-
Comment directement savoir qu'une chaîne de caractères n'est pas un palindrome ?
-
-
Pour le cas général, réduire la chaîne de caractères à étudier en considérant la chaîne de caractères sans le premier ni le dernier caractère.
-
Dans le cas général, la fonction récursive
est_palindromedoit être utilisée. -
Tester le bon fonctionnement de la fonction
maximum_liste.
Interface, pile, file
Écrire une fonction en pseudo code qui permet de supprimer le troisième élément d'une file
Vu au bac.





POO
On considère la classe suivante :
class Personnage:
"""
Un personnage du jeu vidéo
"""
def __init__(self, genre, name, age=0, pdv = 10, life=True):
self.genre = genre
self.name = name
self.age = age
self.pdv = pdv
self.life = life
-
Quel script écrire pour instancier un personnage nommé Galadriel, de genre féminin, d'âge 600 ans, disposant de 40 points de vie?
-
Écrire une méthode
in_life(self)qui vérifie si un personnage est en vie en testant si ses points de vie sont au dessus de 0. La méthode définira le statut du personnage. -
Tester cette méthode sur Galadriel.
-
Écrire une classe
Personnagequi possède trois attributs :-
nomde typestr. -
pdvde typeint. -
qualificationde typestr.
-
-
Instancier deux personnages de la classe
Personnage:-
personnage1 avec nom ='Bob', pdv = 50 et qualification = 'fantassin'.
-
personnage2 avec nom ='Pascual', pdv = 20 et qualification = 'chevalier'.
-
-
Afficher les caractéristiques du personnage Bob afin de vérifier la saisie correcte.
On définit une classe Individu possédant plusieurs attributs : sexe, âge, hobby.
class Individu:
def __init__(self, sexe, age, ho):
"""
sexe : str "M" ou "F" ou "autre"
age:int
ho:list
"""
self.s = sexe
self.a = age
self.h = ho
def estMasculin(self):
"""
renvoie le booléen True si la méthode s'applique sur un individu masculin et False sinon.
"""
return self.s == "M"
Lucie=Individu("F", 17, ["course à pied", "foot", "lecture"])
-
Instancier l'individu Bob agé de 15 ans, de sexe Masculin, et de hobby : tennis, théâtre et couture.
-
Indiquer le script Python pour obtenir la liste des hobbies de Lucie.
-
Écrire une fonction
distAge(individu1, individu2)qui renvoie la différence d'âge entre deux individus, instances de la classeIndividu.
Rappel valeur absolue :abs(val1-val2). -
Indiquer le script Python pour obtenir la différence d'âge en Lucie et Bob.
-
Écrire une fonction
nb_hobby(individu)qui renvoie le nombre de hobby deindividu. -
En vous aidant de la fonction
nb_hobby, écrire en une méthodenbHobbyqui renvoie le nombre de hobby d'un individu.
# Les tests à passer
assert distAge(Lucie,Bob) == 2
assert Lucie.estMasculin() == False
assert Lucie.nbHobby() == 3
assert nb_hobby(Lucie) == 3 Gestion d'une bibliothèque : création d'un système gestion de bibliothèque en Python.
-
Création de la classe
Livre-
Créer une classe
Livreavec pour attributs : un titre, un auteur, un numéro ISBN et un nombre de copies disponibles. -
Créer l'instance ayant pour titre
"La Horde du Contrevent", comme auteur"Damasio Alain", code ISBN"978-2-9522217-0-2"disponible en 3 copies. -
Implémenter une méthode pour emprunter un livre (diminuer le nombre de copies disponibles, gérer l'absence de livre, afficher des informations à l'utilisateur).
-
Implémenter une méthode pour retourner un livre (augmenter le nombre de copies disponibles, informer l'utilisateur du retour par un affichage).
-
Création d'une classe
-
Créer une classe
Bibliothequeavec pour attribut une liste de livres disponibles. -
Implémenter une méthode pour ajouter un livre à la bibliothèque.
-
Implémenter une méthode pour afficher tous les livres disponibles dans la bibliothèque en faisant en sorte d'afficher les caractéristiques de chaque livre.
Tests de vos codes
-
Créer quelques instance de livres et de bibliothèques
-
Ajoutez des livres à la bibliothèque et effectuez des emprunts/retours pour voir si le système fonctionne correctement.
Voici un exercice, qui peut être fait en autonomie, pour tester votre maîtrise de la programmation objet : vous avez à repérer et à corriger des erreurs dans le script proposé.
Cet exercice est issu du site collaboratif de la forge.
Voici un exercice, qui peut être fait en autonomie, pour tester votre maîtrise sur la création de méthodes en programmation objet.
L'exercice est inspiré d'un ancien sujet de baccalauréat, tombé à l'écrit.
Cet exercice est issu du site collaboratif de la forge.
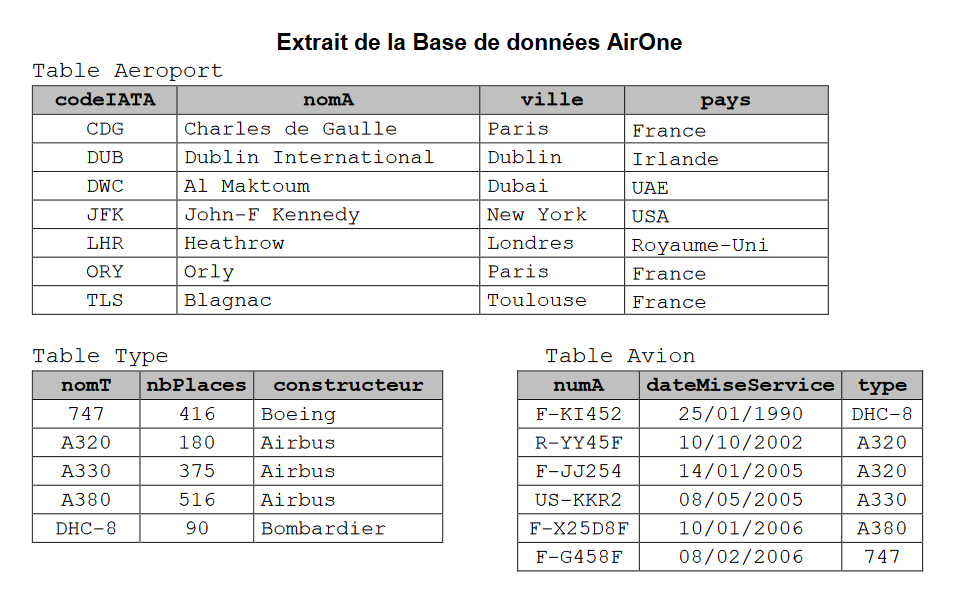
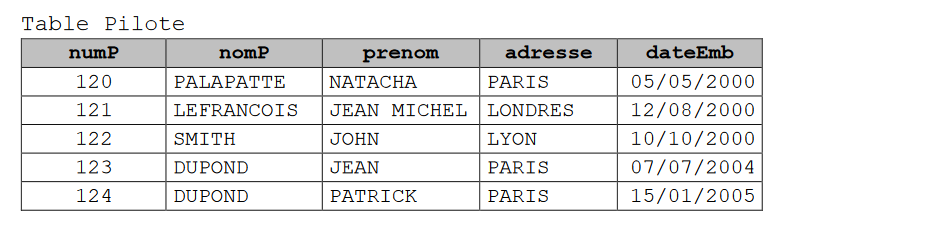
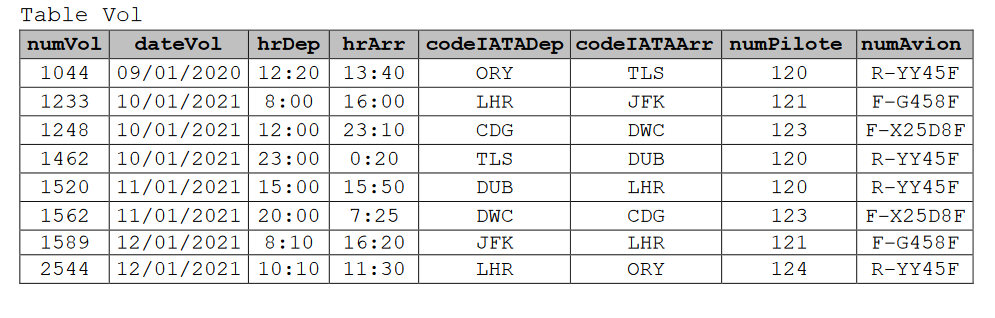
Base de données
Vu au bac.
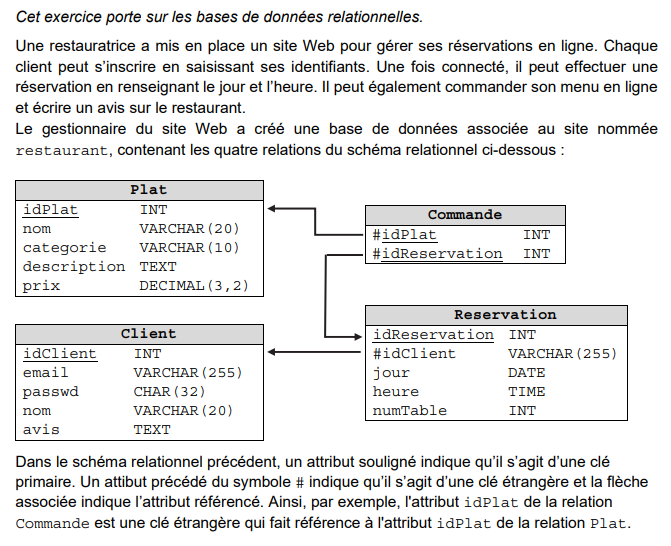
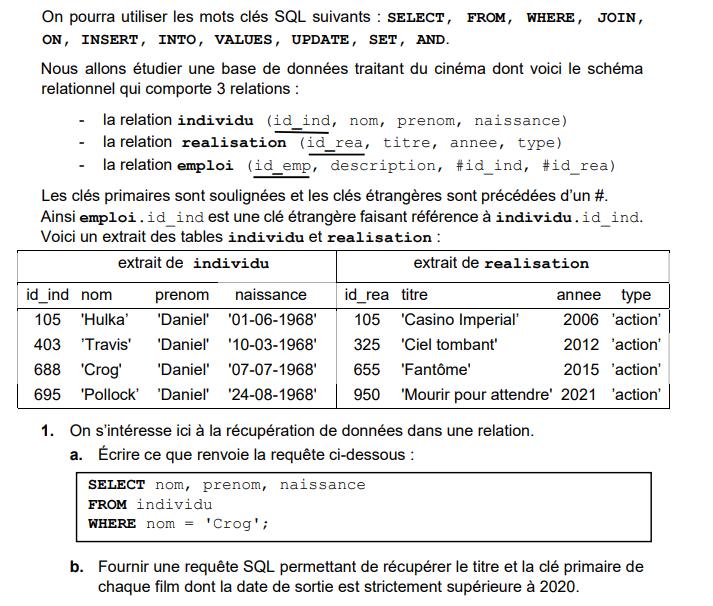
Identifier le vocabulaire du cours sur les bases de données dans ce schéma relationnel
Vu au bac.

Arbres
arbre binaire , poo
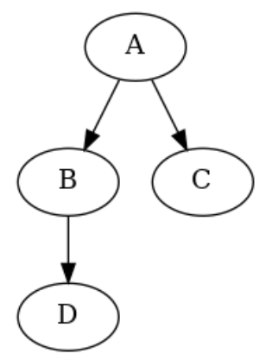
On considère l’arbre binaire suivant :
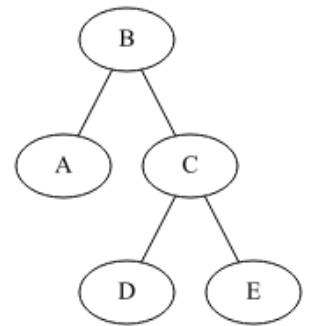
Une implémentation de l’arbre binaire ci-dessus en langage Python a été réalisée à l’aide de la classe Nœud ci-dessous :
class Noeud:
""" Nœud d'un arbre binaire"""
def __init__(self, v, g=None, d=None):
self.valeur = v
self.gauche = g
self.droite = dL'objet représentant cet arbre binaire a été déclaré de la manière suivante :
mon_arbre = Noeud("B", Noeud("A"), Noeud("C", Noeud("D"), Noeud("E")))-
Que renvoie l'instruction mon_arbre.gauche.valeur ?
-
Quelle instruction permet d'afficher la valeur de la feuille "D" de cet arbre ?
-
Dessiner l'arbre a correspondant à la déclaration suivante :
a = Noeud (5, Noeud(12, Noeud(4), Noeud(3)), Noeud(13, None, Noeud(29)))
arbre binaire, poo
Le but de cet exercice est d’implémenter un arbre binaire en programmation objet.
Vous devez pour cela compléter la classe Noeud ci-dessous en respectant les contraintes suivantes :
Le construction __init__ est tel qu’un objet Noeud qui aura 3 attributs :
-
L’attribut
valeurcontiendra la valeur (ou étiquette) associée au nœud. -
L’attribut
gauchecontiendra le sous-arbre gauche. -
L’attribut
droitseront le sous-arbre droit.
Si il n’y a pas de sous-arbre gauche ou droit, on indiquera la valeur None dans les attributs correspondants.
Dans la classe Noeud, vous devez compléter les trois méthodes suivante :
- La méthode
-
La méthode
creer_fils_gauche()prend en paramètre une valeur et crée une feuille à gauche dont la valeur est passée en paramètres. De plus, elle renvoie le nœud fils. -
La méthode
creer_fils_droit()est construite sur le même modèle quecreer_fils_gauche(). De même, elle renvoie le nœud fils.
est_feuille() renverra un booléen selon que l’objet est une feuille de l’arbre ou non.
Exemple d’utilisation de la classe Noeud :
En supposant la classe Noeud créée, voici comment l’arbre ci-dessus peut être implémenté :
>>>arbre = Noeud("A")
>>>sous_arbre_gauche = arbre.creer_fils_gauche("B")
>>>sous_arbre_gauche.creer_fils_gauche("D")
>>>arbre.creer_fils_droit("C")
Quelques vérifications possibles :
>>>arbre.est_feuille()
False
>>>arbre.droit.est_feuille()
True
>>>arbre.gauche.valeur
"B" Compléter le programme ci-dessous
class Noeud():
"""
Implémentation d'un arbre binaire
"""
def __init__(self, valeur):
"""
Constructeur :
valeur est une chaîne de caractères ou un nombre entier.
"""
self.valeur = # À compléter
self.gauche = # À compléter
self.droit = # À compléter
def creer_fils_gauche(self, fils_gauche):
"""
fils_gauche est une chaîne de caractères ou un nombre entier qui sera rajouté comme fils gauche
au nœud de l'arbre binaire sur lequel s'applique cette méthode.
La valeur de ce fils rajouté est renvoyée par la méthode.
"""
self.gauche = # À compléter
return self.gauche
def creer_fils_droit(self, fils_droit):
self.droit = # À compléter
return self.droit
def est_feuille(self):
"""
méthode renvoyant True si le nœud sur lequel s'applique la méthode est une feuille de l'arbre
et False sinon.
"""
# À compléterarbre binaire , poo
On considère l'implémentation suivante :
class Arbre:
def __init__(self, valeur):
self.v = valeur
self.fg = None
self.fd = None
def ajout_gauche(self, val):
self.fg = Arbre(val)
def ajout_droit(self, val):
self.fd = Arbre(val)
def affiche(self):
"""permet d'afficher un arbre"""
if self == None:
return None
else:
return [self.v, Arbre.affiche(self.fg), Arbre.affiche(self.fd)]
def taille(self):
if self == None:
return 0
else:
return 1 + Arbre.taille(self.fg) + Arbre.taille(self.fd)
def hauteur(self):
# Voir la hauteur d'un arbre vide
if self == None:
return 0
elif self.fg == None and self.fd == None :
return 0
else:
return 1 + max(Arbre.hauteur(self.fg), Arbre.hauteur(self.fd))
def get_valeur(self):
if self==None:
return None
else:
return self.v
def racine(self):
if self == None : return None
else: return self.v
def est_feuille(self, noeud):
if self == None : return False
elif self.fg == None and self.fd==None and self.v==noeud : return True
else: return Arbre.est_feuille(self.fg, noeud) or Arbre.est_feuille(self.fd, noeud)
def noeuds(self):
if self ==None : return []
else: return [self.v] + Arbre.noeuds(self.fg) + Arbre.noeuds(self.fd) Le but est de calculer ou de lister :
-
La racine.
-
La liste des nœuds.
-
La liste des feuilles.
-
La liste des nœuds internes.
-
Le nombre de feuilles.
-
Le nombre de branches.
-
L'arité.
-
La taille T(B).
-
La hauteur de B, H(B).
-
LC(B).
-
LCE(B).
-
LCI(B).
-
PM(B).
-
PME(B).
-
PMI(B).
Vous pouvez tester votre code sur cet objet :
abr=Arbre(43)
abr.ajout_gauche(16)
abr.fg.ajout_gauche(8)
abr.fg.ajout_droit(5)
abr.fg.fg.ajout_gauche(99)
abr.fg.fg.fg.ajout_gauche(1)
abr.ajout_droit(36)
abr.fd.ajout_gauche(999)
abr.fd.fg.ajout_gauche(0)
abr.fd.ajout_droit(4)
abr.fd.fd.ajout_droit(6)
abr.fd.fd.fd.ajout_droit(12)
abr.fd.fd.fd.fd.ajout_gauche(9)
abr.fd.fd.fd.fd.ajout_droit(35)
abr.fd.fd.fd.fd.fd.ajout_droit(7)-
Représenter cet arbre.
-
Choisir quelques éléments dans la liste des données à traiter sur cet arbre. A vous d'écrire les méthodes et/ou fonctions supplémentaires pour cet
objetArbre.
arbre binaire , poo
L'implémentation de l'exercice précédent permet d'instancier l'arbre suivant :
abr2=Arbre(13)
abr2.ajout_gauche(10)
abr2.fg.ajout_gauche(5)
abr2.fg.ajout_droit(15)
abr2.fg.fg.ajout_gauche(4)
abr2.fg.fg.fg.ajout_gauche(3)
abr2.ajout_droit(36)
abr2.fd.ajout_gauche(999)
abr2.fd.fg.ajout_gauche(0)
abr2.fd.ajout_droit(14)
abr2.fd.fd.ajout_droit(6)
abr2.fd.fd.fd.ajout_droit(12)
abr2.fd.fd.fd.fd.ajout_gauche(9)
Ce qui donne l'affichage suivant :
[13, [10, [5, [4, [3, None, None], None], None], [15, None, None]], [36, [999, [0, None, None], None], [14, None, [6, None, [12, [9, None, None], None]]]]]-
Représenter sur un feuille de papier l'arbre
abr2. -
Donner ou calculer les éléments suivants :
-
La racine.
-
La liste des noeuds.
-
La liste des feuilles.
-
La liste des noeuds internes.
-
Le nombre de feuilles.
-
Le nombre de branches.
-
L'arité.
-
La taille T(B).
-
La hauteur de B, H(B).
-
LC(B).
-
LCE(B).
-
LCI(B).
-
PM(B).
-
PME(B).
-
PMI(B).
-
arbre binaire de recherche , parcours
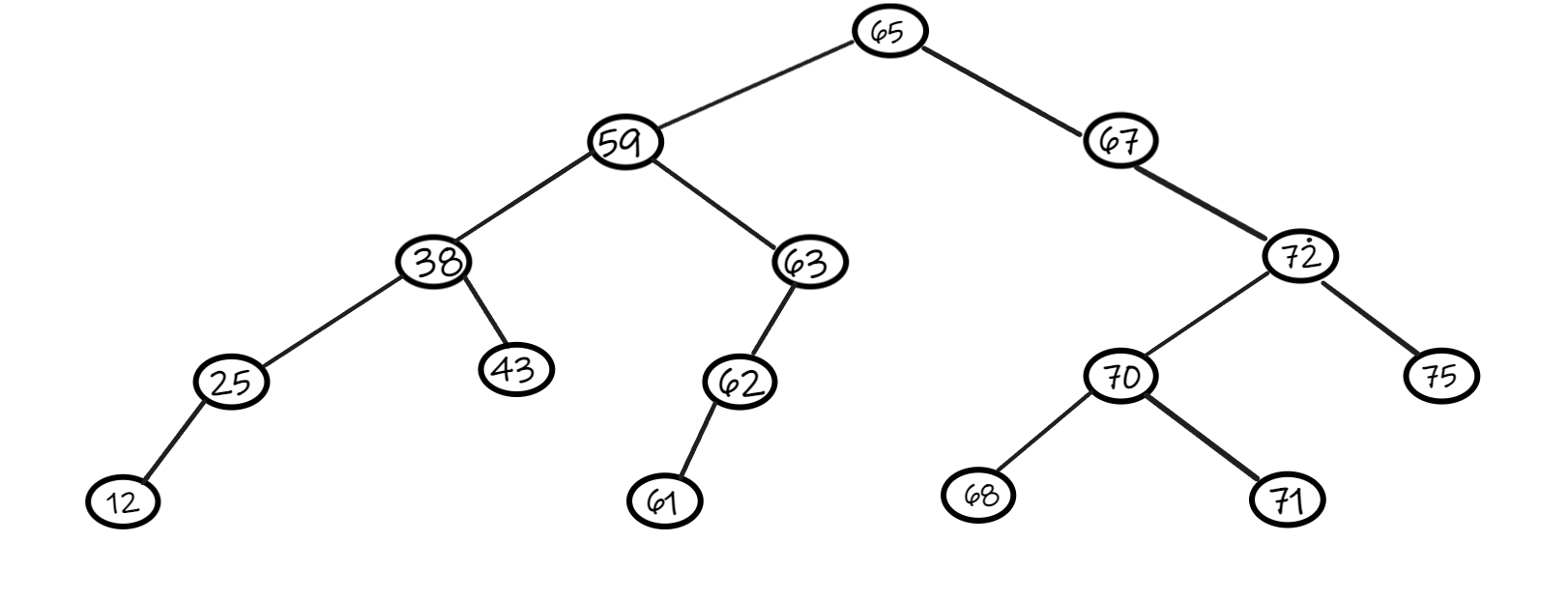
On propose cet arbre binaire :
-
Cet arbre est-il un ABR ?
-
Donner la succession des noeuds visités lors d'un parcours infixe.
-
Donner la succession des noeuds visités lors d'un parcours suffixe.
-
Donner la succession des noeuds visités lors d'un parcours prefixe.
arbre binaire de recherche
Un arbre binaire de recherche est un arbre binaire pour lequel chaque nœud possède une étiquette dont la valeur est supérieure ou égale à toutes les étiquettes des nœuds de son fils gauche et strictement inférieure à celles des nœuds de son fils droit. On rappelle que :
-
sa taille est son nombre de nœuds ;
-
sa hauteur est le nombre de niveaux qu'il contient.
Un éditeur réédite des ouvrages. Il doit gérer un nombre important d'auteurs de la littérature. Pour stocker le nom des auteurs, il utilise un programme informatique qui les enregistre dans un arbre binaire de recherche.
L'arbre vide sera noté Null pour les algorithmes de cet exercice.
Si A est un nœud non vide, valeur(A) renvoie le nom de l'auteur ;
fils_gauche(A) renvoie le fils gauche du nœud A et fils_droit(A) renvoie le fils
droit du nœud A.
L'ordre alphabétique est utilisé pour classer le nom des auteurs.
Par exemple, on a APOLLINAIRE < BAUDELAIRE
Ainsi, pour tout nœud A, si fils_gauche(A) et fils_droit(A) ne sont pas Null, on a :
valeur(fils_gauche(A)) < valeur(A) < valeur(fils_droit(A)).
Par exemple, l'arbre binaire suivant A1 est un arbre binaire de recherche :
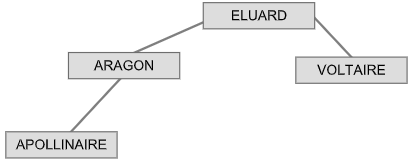
-
-
Recopier et compléter l'arbre binaire de recherche précédent en insérant successivement dans cet ordre les noms suivants : DUMAS ; HUGO ; ZWEIG ; ZOLA.
-
Quelle est la taille de l'arbre obtenu ? Quelle est la hauteur de cet arbre ?
-
Plus généralement, si l'arbre est de hauteur $h$, quel est le nombre maximal d'auteurs enregistrés dans cet arbre en fonction de $h$ ?
-
-
On définit ici l'équilibre d'un arbre binaire : il s'agit d'un nombre entier positif ou négatif. Il vaut 0 si l'arbre est vide. Sinon il vaut la différence des hauteurs des sous-arbres gauche et droit de l'arbre.
Par exemple, si on considère l'arbre suivant que l'on nommera A2.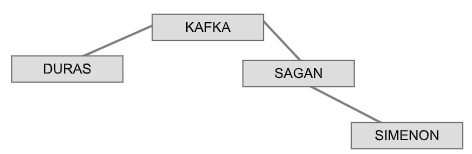
Son équilibre vaut -1 car la hauteur de son sous-arbre gauche vaut 1, la hauteur de son sous-arbre droit vaut 2 et $1 - 2 = -1$ Un arbre est dit équilibré si son équilibre vaut -1, 0 ou 1. L'arbre précédent est donc équilibré.
Recopier et compléter l'arbre de ce dernier exemple avec les noms FLAUBERT, BALZAC, PROUST, SAND, WOOLF, COLETTE, CHRISTIE et AUDIARD quitte à modifier l'ordre d'insertion de manière à ce que cet arbre reste équilibré.
-
L'éditeur souhaite utiliser une fonction récursive
recherche_auteurqui prend en paramètresabrun arbre binaire de recherche etnomun nom d'auteur. La fonction renvoieTruesinomest une étiquette de l'arbreabretFalsedans le cas contraire.On donne la fonction suivante :
def recherche_auteur(abr, nom): if est_vide(abr): return False elif valeur(abr) == nom: return True else: return ...# À complétera. Compléter la dernière ligne de la fonction récursive
recherche_auteur.b. Que renvoie l'appel
recherche_auteur(A2,'SIMENON')? Justifier la réponse -
L'éditeur souhaite utiliser une fonction
hauteur(abr)qui prend en paramètre un arbre binaireabret renvoie la hauteur de cet arbre.Écrire un algorithme de la fonction
hauteur(abr)qui prend en entréeabrun arbre binaire de recherche et renvoie sa hauteur.
On pourra avoir recours aux fonctionsmin(val1, val2)etmax(val1, val2)qui renvoient respectivement la plus petite et la plus grande valeur entreval1etval2.
Graphe
Vous avez créé un réseau social : Typ_au_top.
Pour gérer le réseau, vous l'avez modélisé par un gaphe.
Les membres de votre réseau social sont les sommets du graphe et deux sommets
du graphe sont reliés par une arête si, et seulement si, les deux membres considérés
sont "amis" sur votre réseau social.
Initialement, vous stockiez les informations dans une matrice d'ajacence les informations
permettant de gérer le graphe de votre réseau social.
Comme votre réseau social devient très populaire, on vous conseille de basculer
d'une gestion du graphe basée sur une matrice d'adjacence à une gestion à partir
d'une liste d'adjacence.
-
Supposons que votre réseau social correspond à un graphe de $n$ personnes et $m$ arêtes.
Donner l'ordre de grandeur en fonction de $n$ et de de $m$ des compléxités en mémoire suivantes :-
Coût en mémoire d'un stockage par matrice d'adjacence ?
-
Coût en mémoire d'un stockage par liste d'adjacence ?
-
Expliquer dans quel cas, la complexité en mémoire justifie la pertinence d'une implémentation du graphe à l'aide d'une liste d'adjacence ?
-
-
La liste des membres du réseau est stockée dans une variable
noms.
La matrice gérant initialement le réseau est stockée dans une variableM.
Pour tester la fonction à créer, vous considèrerez les listes réduites suivantes :M = [[0, 1, 1, 0, 0, 0, 1, 0, 0, 1], [1, 0, 0, 0, 1, 0, 1, 0, 1, 0], [1, 0, 0, 1, 1, 0, 0, 1, 0, 0], [0, 0, 1, 0, 0, 0, 0, 1, 0, 1], [0, 1, 1, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 1, 1, 0], [1, 1, 0, 0, 0, 0, 0, 0, 0, 1], [0, 0, 1, 1, 0, 1, 0, 0, 0, 0], [0, 1, 0, 0, 0, 1, 0, 0, 0, 0], [1, 0, 0, 1, 0, 0, 1, 0, 0, 0]] noms = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J"]Compléter la fonction
transferersuivante qui prend en paramètre une matrice d'adjacencematriceet une liste de noms des membreslstet qui renvoie le dictionnaire qui associe à chaque nom de membre la liste d'adjence formée par les amis de ce membre au sein du réseau.def transferer(matrice, lst): dico = ... # création des clés du dictionnaire : les membres du réseau for nom in lst: ... for i in ...: for j in ...: if ... == 1: ... # une ou plusieurs lignes ici return ...Tester la fonction
transfereren utilisant la matriceMet la listenoms. -
Citer une question concrète que l'on pourrait se poser sur des membres du réseau, question à laquelle il sera plus couteux en temps de répondre avec cette implémentation à l'aide de liste d'adjacence plutôt qu'avec l'implémentation sous forme de matrice d'adjacence.
Ordonnancement
| Processus | P1 | P2 | P3 | P4 | P5 |
|---|---|---|---|---|---|
| Durée en quantum | 3 | 7 | 3 | 4 | 6 |
| Date d'arrivée | 5 | 0 | 9 | 2 | 3 |
On considère les processus ci-dessus.
Représenter l'ordonnancement des processus ci-dessus à l'aide du modèle Round Robin.
Algorithmes sur les graphes
Compléter le code de la fonction parcours_dfs_recursive avec les trous à remplir : Vous devez remplir les trous (___) avec les éléments suivants :
-
Initialisez visite avec une liste vide si elle est
None. -
Ajoutez le nœud de départ à la liste des visités.
-
Parcourez les voisins du nœud de départ.
-
Vérifiez si le voisin n'a pas déjà été visité.
-
Faites un appel récursif pour visiter le voisin.
-
Retournez la liste des nœuds visités.
-
Représenter le graphe présent à la fin du code sur une feuille.
def parcours_dfs_recursive(graph, depart, visite=None):
# Si visite est None, initialisez-le avec une liste vide
if ___:
visite = []
# Ajoutez le nœud de départ à la liste des visités
visite.___
# Parcourez les voisins du nœud de départ
for voisin in ___:
# Vérifiez si le voisin n'a pas déjà été visité
if ___ not in ___:
# Appel récursif pour visiter le voisin
parcours_dfs_recursive(___)
# Retournez la liste des nœuds visités
return ___
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F', 'G'],
'D': ['B'],
'E': ['B'],
'F': ['C'],
'G': ['C']
}
depart = 'A'
print(parcours_dfs_recursive(graph, depart))Diviser pour régner
Le but est de trouver un algorithme qui renvoie le couple formé par le minimum et le maximum des éléments d'une liste non vide, algorithme suivant le principe "diviser pour régner".
-
Proposer une fonction
diviserqui prend en praramètre une listelstet renvoie un tuple de deux listes : la première contienne la première moitié des valeurs de la liste tandis que la deuxième contienne la seconde moitié. -
Pour une liste non vide, quels sont les deux cas les plus simples pour obtenir le couple
(minimum, maximum)des éléments de cette liste ? -
On suppose connaître le couple
(min1, max1)d'une listeliste1et celui(min2, max2)d'une listeliste2.
Proposer une fonctionfusionnerqui permet à partir de ces deux couples d'obtenir le couple(minimum, maximum)oùminimumest le minimum de l'ensemble des deux listesliste1etliste2etmaximumen est le maximum.Par exemple,
fusionner((2, 6), (4, 7))renvoie le tuple(2, 7). -
Proposer une fonction récursive
extrema_DPRqui prend en paramètre une listelst, qui, en utilisant le paradigme "diviser pour régner" et les fonctions précédentes, permet d'obtenir le couple(minimum, maximum)de la listelst. -
La compléxité en temps de cette fonction
extrema_DPRest surement de l'ordre de $O(nlog_2(n))$, si vous l'avez écrite similairement à celle vue en cours donnant le tri par fusion.
L'utilisation du principe "diviser pour régner" apporte-t'il une diminution de la complexité par rapport à un balayage naïf des éléments de la liste ?

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International