Table of Contents

    Aide-mémoire de l'utilisation de sympy

    • Le nombre pi s'écrit pi
    • Le nombre i s'écrit I
    • Le nombre e s'écrit E
    • L'infini s'écrit oo (deux 'o')

    http://docs.sympy.org/0.7.2/tutorial.html

    In [1]:
    from sympy import *
x=Symbol('x')
    In [2]:
    x**2+3*x+2+4*x-3
    Out[2]:
    x**2 + 7*x - 1
    In [3]:
    expr=x**2+4*x-1
diff(expr,x) # pour une dérivée
    Out[3]:
    2*x + 4
    In [4]:
    expr=log(1-x**2)
series(expr,x,0,8) # Pour un DL
    Out[4]:
    -x**2 - x**4/2 - x**6/3 + O(x**8)
    In [5]:
    solve(x**2+x+1,x) # Résoudre une équation dans les complexes.
    Out[5]:
    [-1/2 - sqrt(3)*I/2, -1/2 + sqrt(3)*I/2]
    In [6]:
    y=Symbol('y')
((x+y)**2).expand() # Le développement
    Out[6]:
    x**2 + 2*x*y + y**2
    In [7]:
    expand((x+1)**2)
    Out[7]:
    x**2 + 2*x + 1
    In [8]:
    factor(x**2-1) # La factorisation
    Out[8]:
    (x - 1)*(x + 1)
    In [9]:
    (x**2).subs(x,x+1) # La substitution
    Out[9]:
    (x + 1)**2
    In [10]:
    limit(1/(x+1),x,oo)
    Out[10]:
    0
    In [11]:
    integrate(1/x,x)
    Out[11]:
    log(x)
    In [12]:
    integrate(1/x,(x,1,E))
    Out[12]:
    1
    In [15]:
    init_printing() # Pour faire des rendus du type latex
Integral(sqrt(1/x),x) # Pour dessiner l'intégrale et interpréter sqrt(x)
    Out[15]:
    $$\int \sqrt{\frac{1}{x}}\, dx$$
    In [14]:
     Matrix([[1, -1], [3, 4], [0, 2]])
    Out[14]:
    $$\left[\begin{matrix}1 & -1\\3 & 4\\0 & 2\end{matrix}\right]$$
    In [16]:
    # La liaison avec graphviz
from sympy.abc import x,y
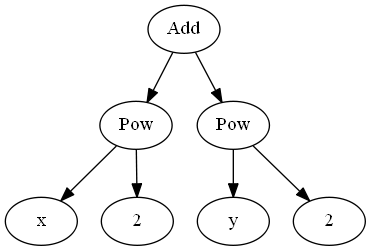
print(dotprint(x**2+y**2))

    digraph{

# Graph style
"ordering"="out"
"rankdir"="TD"

#########
# Nodes #
#########

"Add(Pow(Symbol(x), Integer(2)), Pow(Symbol(y), Integer(2)))_()" ["color"="black", "label"="Add", "shape"="ellipse"];
"Pow(Symbol(x), Integer(2))_(0,)" ["color"="black", "label"="Pow", "shape"="ellipse"];
"Symbol(x)_(0, 0)" ["color"="black", "label"="x", "shape"="ellipse"];
"Integer(2)_(0, 1)" ["color"="black", "label"="2", "shape"="ellipse"];
"Pow(Symbol(y), Integer(2))_(1,)" ["color"="black", "label"="Pow", "shape"="ellipse"];
"Symbol(y)_(1, 0)" ["color"="black", "label"="y", "shape"="ellipse"];
"Integer(2)_(1, 1)" ["color"="black", "label"="2", "shape"="ellipse"];

#########
# Edges #
#########

"Add(Pow(Symbol(x), Integer(2)), Pow(Symbol(y), Integer(2)))_()" -> "Pow(Symbol(x), Integer(2))_(0,)";
"Add(Pow(Symbol(x), Integer(2)), Pow(Symbol(y), Integer(2)))_()" -> "Pow(Symbol(y), Integer(2))_(1,)";
"Pow(Symbol(x), Integer(2))_(0,)" -> "Symbol(x)_(0, 0)";
"Pow(Symbol(x), Integer(2))_(0,)" -> "Integer(2)_(0, 1)";
"Pow(Symbol(y), Integer(2))_(1,)" -> "Symbol(y)_(1, 0)";
"Pow(Symbol(y), Integer(2))_(1,)" -> "Integer(2)_(1, 1)";
}

    Le rendu à l'aide de graphviz en tant que graphe

    In [ ]: