Demander le programme
Repérage sur Terre
Méridiens et parallèles
Voici ci-dessous une schématisation de la Terre avec des lignes imaginaires.
Déplacer les curseurs pour obtenir les coordonnées approchées de votre ville.
( ; )
compléter les deux définitions suivantes en utilisant les mots méridiens et parallèles :
Les sont des cercles imaginaires situés dans des plans parallèles au plan de référence qui coupe la Terre en deux hémisphères Nord et Sud. Ces cercles sont repérés par rapport au grand cercle de référence : l'équateur
Les sont des demis grands cercles imaginaires reliant les pôles Nord et Sud. Ces cercles sont repérés par rapport au grand cercle de référence : le méridien de Greenwich
Longitudes et latitudes
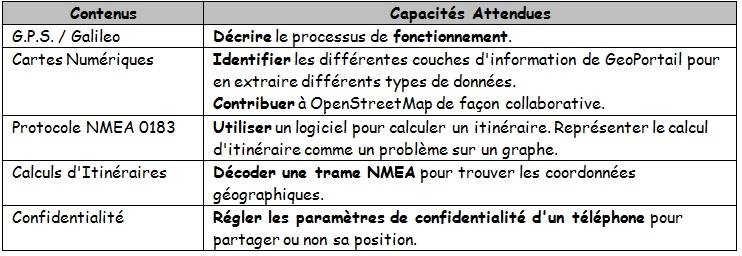
Un point situé A sur un parallèle (demi-grand cercle noir sur l'image) donné est aussi l'image d'un point de l'équateur par une rotation, vers le Nord ou le Sud : l'angle $\phi$ de cette rotation est la latitude du parallèle.
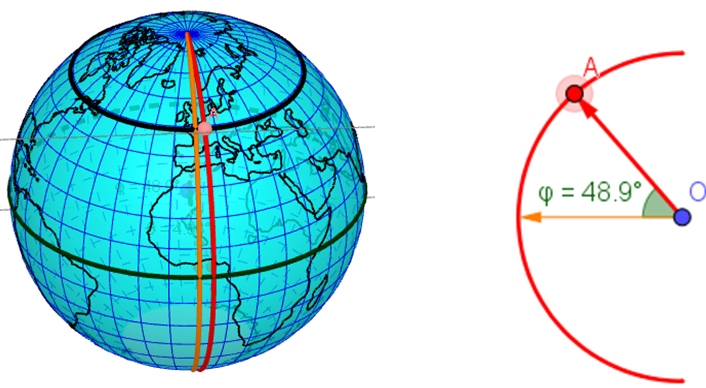
Un méridien donné (celui rouge) et le méridien de Greenwich (demi-grand axe orange) déterminent, par rapport à l'axe Nord-Sud de la planète, un angle $\theta$ : c'est la longitude du méridien.
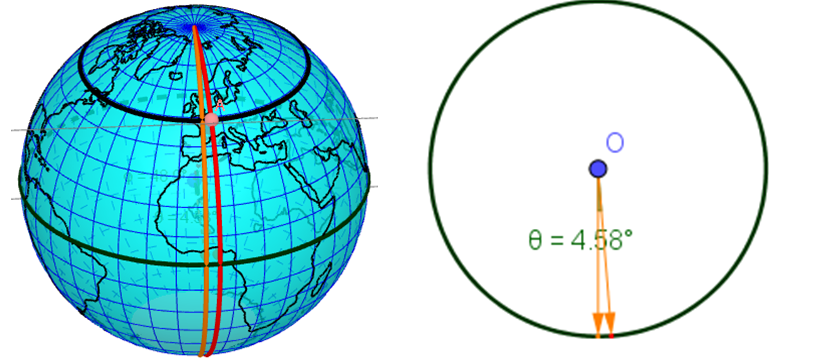
Les coordonnées géographiques sont exprimées soit :
-
selon une notation sexagésimale : les angles sont exprimé en degrés (°), minutes (') correspondant au 1/60 d'un degré et secondes (").
-
selon une notation décimale : les angles sont exprimés en degrés avec des nombres décimaux (à virgule).
L'Arc de Triomphe situé à Paris a pour coordonnées :
-
$(48.873332 ; 2.294699)$ en notation décimale.
-
$(48°52'24" N ; 2°17'41" E)$ en notation sexagésimale.
-
$N$ signifie que le lieu se situe dans l'hémisphère nord (au nord de l'équateur).
-
$E$ signifie que le lieu se situe à l'ouest du méridien de Greenwich (en gros à l'ouest par rapport à Londres).
-
Aller sur le site https://www.coordonnees-gps.fr afin de vérifier les coordonnées de l'exemple précédent.
-
Déterminer l'altitude de l'Arc de Triomphe de Paris.
Tout point de la Terre est déterminé par ses coordonnées géographiques (la latitude et la longitude) et par son altitude (élévation par rapport au niveau de la mer).
-
Sachant qu'il y a 60 minutes par degré, convertir en notation décimale cette latitude sexagésimale : $48° 20'$.
-
Sachant qu'il y a 60 minutes par degré et 60 secondes par minutes, convertir en notation décimale cette longitude sexagésimale : $17° 49' 11"$.
-
Aller sur le site https://www.coordonnees-gps.fr afin de vérifier la cohérence des coordonnées précédemment obtenues.
Quelle ville de l'hémisphère Nord à l'Est de Greenwich se situe à ces coordonnées géographiques ?
-
Copier_coller dans Edupython le code ci-dessous et remplacer les $...$ de la ligne 9 par une formule :
def convertisseur_decimal(degre, minute, seconde): """ fonction qui : prend en argument trois nombres entiers, convertit une coordonnée donnée par sa valeur en degrés, minutes et secondes en sa valeur décimale, renvoie la valeur décimale de cette coordonnée. Exemple : convertisseur_decimal(17,49,11) renvoie 17.81972222222222""" angle = ... # ... à remplacer par votre code return angle
-
Sachant qu'il y a 60 minutes par degré, convertir en notation sexagésimale cette latitude décimale : $56.8$.
-
Sachant qu'il y a 60 minutes par degré et 60 secondes par minutes, convertir en notation sexagésimale cette latitude décimale : $60.591389$.
-
Aller sur le site https://www.coordonnees-gps.fr afin de vérifier la cohérence des coordonnées précédemment obtenues.
Quelle ville de l'hémisphère Nord à l'Est de Greenwich se situe à ces coordonnées géographiques ?
-
Copier_coller dans Edupython le code ci-dessous et remplacer les $...$ des lignes 11à 13 par une formule :
from math import floor def convertisseur_sexagesimal(decimale): """ fonction qui : prend en argument un nombre flottant (à virgule), convertit une coordonnée donnée par sa valeur décimale en sa valeur hexadécimale : degre, minute, seconde (3 nombres entiers) renvoie le triplet formé de ces trois nombres. Exemple : convertisseur_decimal(60.59139) renvoie 60 , 35 , 29""" degre = ... # ... à remplacer par votre code minute = ... # ... à remplacer par votre code seconde = ... # ... à remplacer par votre code return degre, minute, secondeLa fonction
floordu module maths permet d'obtenir la partie entière d'un nombre réel, c'est à dire, pour un nombre positif, cette fonction enlève l'ensemble des nombres derrière la virgule.floor(3.14159)renvoie le nombre entier 3.
Pour les plus rapides :
Déplacer les curseurs de méridien et de parallèle afin de repérer sur la Terre les premières villes proposées.
Triangulation
Un trésor a été caché. 3 personnes se liguent pour le trouver : Bob, Olaf et Ramia. La personne qui a caché l'objet donne à chacun une information :
-
Bob se trouve à 10 mètres du trésor,
-
Olaf à 15 mètres,
-
Ramia à 8 mètres.
En utilisant le fichier Geogebra ci-dessous, trouver le lieu où est caché le trésor.
L'unité est le mètre et penser à utiliser l'onglet Cercle (centre-rayon)

Compléter la propriété suivante :
Pour pouvoir se repérer dans un plan, il suffit de connaître distances par rapport à des points de repère.
Tout point de la Terre est déterminé par des coordonnées géographiques : latitude, longitude et altitude.
La latitude d'un lieu correspond à l'angle formé par la parallèle passant par ce lieu avec l'équateur.
La longitude d'un lieu correspond à l'angle formé par le méridien passant par ce lieu avec le méridien de Greenwich (proche de Londres).
Les systèmes de géolocalisation
Définition
Donner une définition du principe de la géolocalisation à l’aide de la vidéo accessible avec ce lien.
Fonctionnement du GPS
Le but est de répondre aux questions suivantes à l'aide de deux vidéos.
L'ensemble des questions se trouve format modifiable ici ou en format .pdf ici.
-
Pourquoi la localisation peut être un peu imprécise ?
-
Depuis quelle date fonctionne le GPS ?
-
Quel objet est nécessaire au fonctionnement du GPS ?
-
Quelles sont les deux principales informations contenues dans les messages envoyés par les satellites ?
-
Comment est calculée par le récepteur la distance le séparant d'un satellite ?
-
À quelle erreur de distance conduit une erreur de 0.001 secondes ?
-
Quel facteur de précision gagne-t-on avec le système européen Galileo par rapport au système américain GPS ?
-
Quel est le principe de la trilatération ?
-
Pourquoi un quatrième satellite est nécessaire ?
-
Quelle est la précision de la synchronisation des satellites et du récepteur ?
-
En plus des satellites, quelles autres infrastructures sont nécessaires ?
Visionner la vidéo accessible à cette adresse Puis répondre aux questions suivantes :
En complément, visionner cette vidéo sur le système Galileo se trouvant à cette adresse, puis répondre aux questions suivantes :
La géolocalisation est la connaissance de la position sur Terre : elle permet d'avoir la latitude, la longitude et l'altitude.
Les systèmes américain GPS et européen Galiléo permettent la géolocalisation d'un récepteur à partir d'au moins quatre satellites.
Ils utilisent le décalage temporel entre l'heure d'émission par un satellite et celle de réception d'un message radio pour mesurer la distance approchée entre le récepteur et ces satellites. À partir de ces distances, le récepteur calcule ses coordonnées géographiques sur Terre (latitude, longitude et altitude) : c'est la trilatération.
Le quatrième satellite sert à corriger d'éventuels problèmes d'horloge : il y a synchronisation.
Les cartes numériques
Un exemple de carte numérique : GEOPORTAIL
Le Géoportail est un portail Web public permettant l'accès à des services de recherche et de
visualisation de données géographiques ou géolocalisées.
Il a notamment pour but de publier les données géographiques de référence de l'ensemble du territoire
français.
Vous pouvez vous rendre sur le site de Géoportail via le lien ci dessous :
Géoportail est donc un portail accessible fourni par l’administration française.
Les informations sont directement issues des services administratifs français tels que le cadastre,
les ponts et chaussées …
Un autre : OPENSTREETMAP
Il existe depuis peu un portail opensource : OPENSTREETMAP.
accès direct à OPENSTREETMAP
Chacun peut accéder aux données d'OpenStreetMap, les modifier ou en ajouter.
Chacun peut utiliser les données d'OpenStreetMap pour des applications non commerciales.
Différentes applications pour des automobilistes, des cyclistes, des personnes handicapées à
mobilité réduite, des skieurs, des randonneurs, ... ont été créées à partir de la base de données
d'OpenStreetMap.
Pour les plus curieux
Un exemple d'application est par exemple le geocaching.
Ce jeu est une chasse au trésor. Des individus ont cachés dans différents endroits des objets
et ont seulement donné le positionnement GPS de cette cache (voire quelques indices).
Plusieurs millions de tels "trésors" à trouver ont des informations disponibles sur le site
officiel de geocaching.
-
Aller sur le site officiel.
-
Se connecter à l'aide :
-
de l'identifiant : SNTReims
-
du mot de passe : SNTReims
-
-
Chercher les coordonnées GPS de l'objet nommé "La dame" caché à Vitry-le-François.
-
Visualiser la carte qui apparaît et qui sert à aider les personnes à trouver l'objet caché. D'où viennent les données ayant permis la réalisation de la carte affichée ?
Les informations présentes sur les cartes d'OpenStreetMap peuvent être mises à jour ou corrigées par tout à chacun.
Pour les plus curieux
si vous regardez la carte du lycée, vous verrez que certains éléments manquent comme par exemple des arbres.
Si vous êtes intéressé.e.s, vous pouvez créer un compte sur ce site afin de compléter les manques observés.
Il existe plusieurs sites Internet qui proposent des cartes numériques :
-
Géoportail est un site public français permettant l'accès aux données publiques géolocalisées et fiables. L'utilisateur peut superposer sur un fond de carte différentes couches de données.
-
OpenStreetMap est un service de cartographie libre et collaboratif. Chacun peut y contribuer en modifiant ou en rajoutant des informations.
Le protocole NMEA
Nous avons maintenant des informations sur le fonctionnement physique d’un système de géolocalisation
et avons vu la mise en pratique via Géoportail et OpenStreetMap.
Mais comment le logiciel de carte numérique connaît-il les positions GPS ?
Rappel de ce qui a déjà été vu dans des vidéos précédentes
Votre récepteur GPS (Smartphone) reçoit des signaux depuis les satellites des différentes constellations
de satellites servant à la géolocalisation (GPS (États-Unis), Galileo(Union Européenne), Glonass(Russie),
Baidou(Chine)).
En traitant des données, il calcule votre position géographique : coordonnées et altitude. Le récepteur
envoie ces informations sous forme de phrases électroniques appelées "trames" à différentes applications
installées sur votre Smartphone.
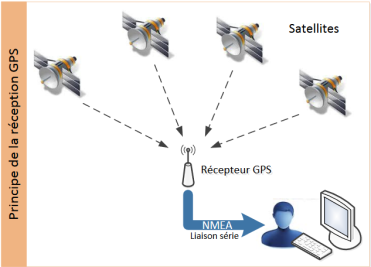
Protocole NMEA
Afin que toutes les applications puissent utiliser ces "trames", il est nécessaire que le format de ces phrases suivent des normes fixes.
Compléter la définition suivante qui a déjà été vue dans le thème Internet :
En informatique, un ensemble de normes permettant à différents périphériques informatiques de dialoguer entre eux en réseau est appelé un .
Pour les trames issues de récepteurs GPS, les normes du protocole sont définies et contrôlées par la National Marine Electronics Association (NMEA), association américaine de fabricants d'appareils électroniques maritimes. Pour cette raison, on parle de protocole NMEA.
Il y a deux Normes NMEA :
-
le NMEA 0183 qui a l’avantage d’être « lisible » mais qui est basée sur une communication série assez lente, peu performante et plus complexe à mettre en réseau.
-
Une plus récente le NMEA 2000 qui n’est pas directement « lisible », beaucoup plus rapide et simple à installer en réseau.
La seule norme au programme de SNT est celle NMEA 0183 car cette trame est lisible.
Une trame NMEA (sous-entendu NMEA 0183) est donc une suite de caractères contenant des informations de géolocalisation comme :
-
la latitude, la longitude,
-
l'altitude,
-
le nombre de satellites,
-
l'heure, la date, …
Utilisation d'une trame NMEA
Au vu de vos compétences informatiques poussées, vous avez été recruté.e.s comme membre du
contre-espionnage français : félicitations !
Vous avez installé une application pirate dans le Smartphone d'une personne que vous avez à
surveiller. Cette application vous renvoie à heures fixes les trames NMEA du récepteur GPS
du smartphone espionné.
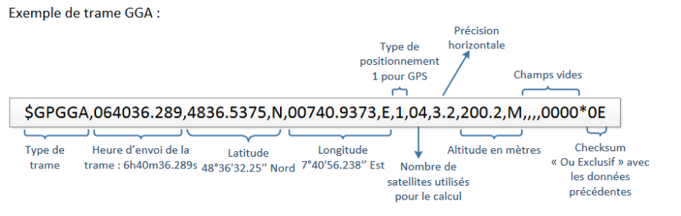
Voici la trame transmise :
$$\$GPGGA,104022.313,4851.4956,N,00217.6699,E,1,05,3.2,323.1,M,,,,0000*0E$$
Vous avez deux questions auxquelles vous devez répondre pour la surveillance établie :
-
À quelle heure le récepteur a-t-il envoyé cette trame ?
-
Où peut donc se trouver la personne que vous surveillez ?
Pour déchiffrer la trame NMEA et répondre à ces questions, vous avez utiliser les compléments d'informations du petit manuel de l'espion donné votre service de contre-espionnage :
|
Complément 1 : sur les deux premiers caractères après le symbole $\$$ : Les deux premiers caractères suivant $\$$ permettent d'identifier les satellites qui sont à l'origine des signaux reçus. Les principaux préfixes sont :
|
|
|
Complément 2 issu du site de Wikipédia :
|
|
|
Complément 3 sur le calcul de la valeur de la latitude : Le troisième élément de la trame NMEA donne la valeur de la latitude écrite de manière compliquée. Pour retrouver la coordonnées en DMS (Degré, Minutes et Secondes), sachez que :
Dans $\$GPGGA,092750.000,5732.4296,N,00444.0390,O,1,08,1.4,15.8,M,,,,0000*35$ : La latitude est donnée par $57 \color{red}{32} \color{blue}{.4296}$ ; La latitude est donc de : Ainsi, la latitude est de 57°32'25.776". |
|
-
À heure le récepteur a-t-il envoyé cette trame ?
-
Où peut donc se trouver la personne que vous surveillez ?
-
Voici un exemple de trame GPS, quelle est la ville indiquée par cette trame :

-
Voici un autre exemple de trame GPS, quelle est la ville indiquée par cette trame :
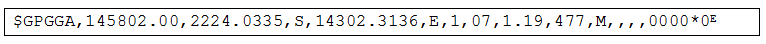
-
Voici un autre exemple de trame GPS, quelle est la ville indiquée par cette trame :
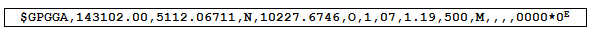
Déterminer le lieu ou la photo a été prise :

La liste des données Exif (Exchangeable Image file format) intégrées par vos appareils photos numériques regroupe une foule d'informations parmi lesquelles :
-
la date et l'heure à laquelle la photo a été prise,
-
les coordonnées GPS, ...
Certains sites web comme https://www.metadata2go.com/ permettent d’obtenir tout un ensemble de données sur la photo.
Utilisation d'un code Python pour automatiser l'étude d'une trame NMEA
Comme en réalité, votre récepteur envoie de nombreuses trames chaque minute, il est préférable en tant qu'espion que vous automatisiez la localisation de la personne suivie directement sur une carte.
Code à comprendre
-
Voici ci-dessous un code à saisir (par copie ou par saisie) sur EduPython (il est inutile de saisir les commentaires commençant par le symbole dièse #) :
import webbrowser # bibliothèque permet d'interagir avec le navigateur zoom='16' # Faire des essais avec différentes valeurs pour comprendre le rôle de ce paramètre latitude=55.75025 longitude=37.6205 webbrowser.open("https://www.openstreetmap.org/#map=" + zoom + "/" + str ( latitude ) + "/" + str ( longitude)) -
Saisir puis exécuter le script précédent.
Que se passe-t-il au moment de l'exécution ? -
Que remarquez-vous quand aux éléments apparaissant dans l'URL ?
-
Quelle ville est représentée ?
Code à comprendre
-
Voici ci-dessous un code à saisir (par copie ou par saisie) sur EduPython (il est inutile de saisir les commentaires commençant par le symbole dièse #) :
import webbrowser # bibliothèque permet d'interagir avec le navigateur zoom='16' # Faire des essais avec différentes valeurs pour comprendre le rôle de ce paramètre latitude=55.75025 longitude=37.6205 webbrowser.open("https://www.openstreetmap.org/#map=" + zoom + "/" + str ( latitude ) + "/" + str ( longitude)) -
Saisir puis exécuter le script précédent.
Que se passe-t-il au moment de l'exécution ? -
Que remarquez-vous quand aux éléments apparaissant dans l'URL ?
-
Quelle ville est représentée ?
Premières utilisations du script
Voici différentes trames.
Pour chacune des trames ci-dessous, calculer à la main la latitude et la longitude en degrés décimaux, puis utiliser le programme Python de l'exercice précédent pour localiser la ville et l'État correspondant à la trame.
-
Trame 1 : $\$GAGGA,145923.12,5230.9720,N,01322.6620,E,1,08,0.21,41,M,,,,0000*0E$.
-
Trame 2 : $\$GPGGA,085416.23,4850.8956,N,06732.9298,O,1,06,2.35,1,M,,,,0000*0E$.
-
Trame 3 : $\$GPGGA,194701.45,2612.3990,S,02802.6016,E,1,06,2.35,1,M,,,,0000*0E$.
Automatiser le programme en Python
La valeur de la latitude, sans le signe, est présente dans une trame NMEA 0183 en troisième position.
Il est possible d'extraire automatiquement par un programme cette information pour la transformer en un résultat en degrés décimaux.
Voici ci dessous le script en python d'une fonction latitude qui renvoie la latitude
(sans le signe et en degrés décimaux) d'un lieu à partir d'une trame NMEA 0183.
Le script est téléchargeable ici.
-
Lire les commentaires (précédés d'un symbole #) afin de comprendre comment fonctionne cette fonction.
-
Pour obtenir la fonction longitude qui renvoie la longitude (sans le signe et en degrés décimaux) d'un lieu à partir d'une trame NMEA 0183, il suffit de reprendre le code de la fonction latitude avec quelques modifications.
-
Quelles sont les modifications à faire pour avoir une telle fonction
longitude? -
Programmer cette fonction
longitudesur EduPython puis tester cette fonction, par exemple avec la trame : $\$GPGGA,194701.45,2612.3990,S,02802.6016,E,1,06,2.35,1,M,,,,0000*0E$ :
Il suffit dans la console de lancer successivement les deux lignes suivantes :trame = "$GPGGA,194701.45,2612.3990,S,02802.6016,E,1,06,2.35,1,M,,,,0000*0E" longitude(trame)Normalement, l'affichage obtenu doit être : 28.04336
-
-
On a déjà vu que la latitude d'un lieu est en fait un nombre avec un signe :
-
si le lieu est situé dans l'hémisphère nord, alors la latitude est positive,
-
sinon la latitude est négative.
Dans une trame NMEA 0183, la position par l'équateur est donnée par 1 lettre :
-
N : si le lieu est situé dans l'hémisphère nord,
-
S : si le lieu est situé dans l'hémisphère sud.
Voici ci-dessous le script de la fonction
signe_latitude.
Cette fonction fera appel à la fonction latitude étudiée précédemment pour renvoyer la latitude, avec son signe, du lieu correspond à la trame entrée comme paramètre.Compléter la ligne 8 :
if ..........afin que cette fonction soit opérante.-
n'oubliez pas de mettre des guillemets
"pour définir une chaîne de caractères, -
ne pas confondre l'affectation avec
=et la comparaison avec==.
def signe_latitude(trame): """fonction qui renvoie la latitude du lieu avec son signe en degré décimal (positive si dans l'hémisphère Nord, négative sinon) à partir de la trame NMEA 0183 entrée comme paramètre""" liste_information=trame.split(",") # liste des éléments composants la trame if ........................................................................ return(latitude(trame)) else: return(-latitude(trame)) -
-
On a déjà vu que la longitude d'un lieu est en fait un nombre avec un signe :
-
si le lieu est situé à l'est du méridien de Greenwich, alors la longitude est positive,
-
sinon la longitude est négative.
Dans une trame NMEA 0183, la position par l'équateur est donnée par 1 lettre :
-
O : si le lieu est situé à l'ouest du méridien de Greenwich,
-
E : si le lieu est situé à l'est du méridien de Greenwich.
Modifier le code de la question précédente donnant la fonction
signe_latitudepour obtenir une fonctionsigne_longitudequi renvoie la longitude, avec son signe, du lieu correspond à la trame entrée comme paramètre. -
-
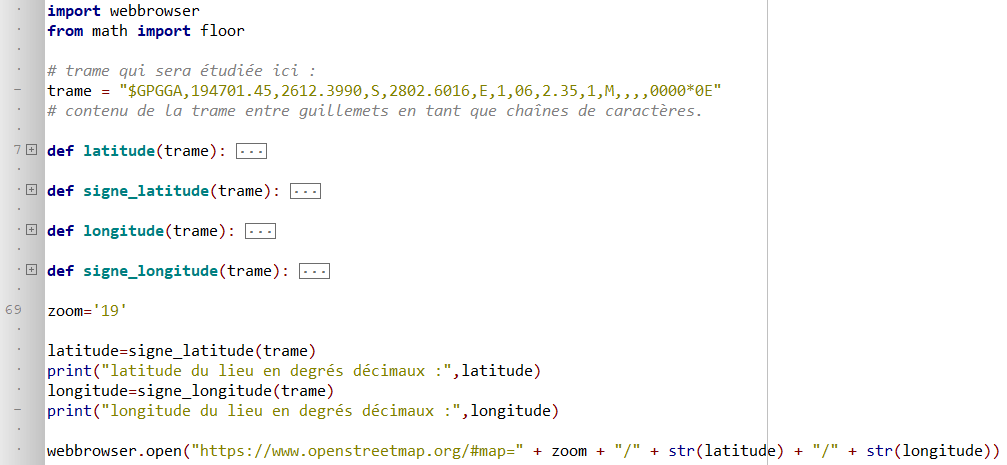
Pour obtenir un script complet qui affiche les coordonnées du lieu en degrés décimaux et permet la visualisation sur OpenStreetMap, il suffit de rassembler les différentes fonctions précédentes dans un même programme en suivant la structure du code apparaissant ci-dessous :
-
Le faire.
-
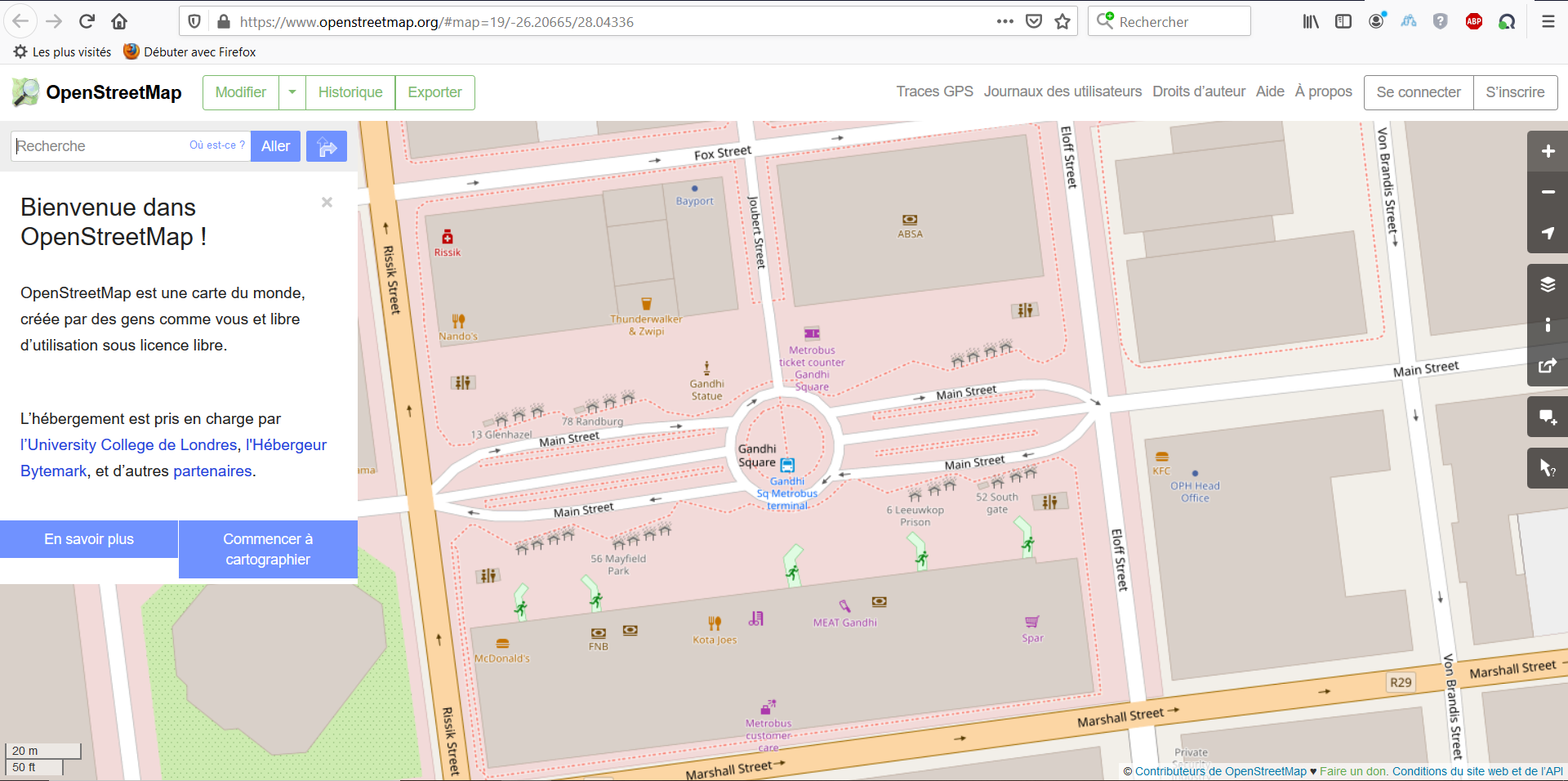
Tester votre programme en l'exécutant avec la trame suivante : $\$GPGGA,194701.45,2612.3990,S,02802.6016,E,1,06,2.35,1,M,,,,0000*0E$
Il doit faire faire afficher :-
latitude du lieu en degrés décimaux : -26.20665
-
longitude du lieu en degrés décimaux : 28.04336
-
et doit faire apparaître l'image ci-dessous dans le navigateur :
-
-
Pour utiliser le script, il suffit de remplacer la trame de la ligne 5 en remplaçant la chaîne de caractères entre guillemets " par la trame voulue.
Le but de cette partie est surtout que vous preniez le réflexe de refuser (sauf cas exceptionnel) toute géolocalisation.
En particulier sur vos téléphones portables, de nombreuses applications de
jeux, d'informations météo, de sports, d'annonce vous demandent de partager
par défaut votre géolocalisation.
La géolocalisation n'est pas nécessaire au bon fonctionnement de l'application
mais les entreprises gérant ces applications utilisent ces informations pour gagner
de l'argent à vos dépends.
En effet, ces informations sont transmises à des régies publicitaires ou des
modules techniques en lien avec ces applications puis sont centralisés par des
databrokers, c'est-à-dire des courtiers de données qui vont vendre des lots
de données à qui veut les acheter pour des fin commerciale ou autres.
Voici le lien vers un article de mars 2025 lié une enquête de Franceinfo
qui montre comment ces données peuvent de géolocalisation peuvent exposer la vie
privée de militaires, de diplomates ou de politiques français.
En particulier cet article montre qu'il est assez facile de trouver
l'identité d'une personne simplement à partir de plusieurs données de
géolocalisation.
Voici le lien vers un article de janvier 2025 du Monde
qui montre comment des applications grand public facilitent
le pistage de leurs
utilisateurs à leur insu et comment ces données sont revendues voire
parfois piratées à des fins crapuleuses.
Soyez attentifs aux autorisations auxquelles vous consentez en
installant une application et n'acceptez que le strict nécessaire.
Pour réduire les autorisations de pistage de votre téléphone par
géolocalisation, vous pouvez modifier les paramètres de votre smartphone :
-
Sur iOS : "Réglages" > "Confidentialité et sécurité" > "Suivi" > Décocher "Autorisation du suivi par les apps".
-
Sur Android : "Réglages" > "Confidentialité" > "Publicités" > "Supprimer l'identifiant publicitaire".
Les informations de géolocalisation peuvent être regroupés dans un message composés de caractère respectant un certain nombre de protocoles (= règles) : c'est la trame NMEA. La trame NMEA 0183 est créée par le récepteur GPS d'un objet comme un smartphone à partir des informations issues de satellites. Les différentes informations contenues sont séparées par une virgule.
Il est possible de décoder une trame NMEA 0183 pour obtenir en particulier les informations suivantes :
-
heure d'envoi de la trame,
-
la latitude du lieu,
-
la longitude du lieu,
-
l'altitude du lieu,
Sauf temporairement en cas d'un service rendu qui vous serez nécessaire, refusez de partager votre géolocalisation afin de protéger vos données personnelles.
Calculs d'itinéraires
Organisation d'un voyage
Vous avez prévu de vous rendre en voiture à Gibraltar (au sud de l'Espagne). Vous prenez en partant un.e ami.e à Vitry-le François. Vous désirez savoir quel chemin vous sera le plus rapide entre Vitry-le François et Gibraltar.
Il existe différent sites Web comme Mappy, Via Michelin, OpenStreetMap et Google Maps, qui permettent de conseiller plusieurs itinéraires selon des critères prédéfinis par l'utilisateur.
-
-
Aller sur le site Mappy.
-
Gérer correctement les cookies (en faisant en sorte de refuser le maximum de cookies !) et la géolocalisation (en la refusant !).
-
Prendre une copie de l'image du trajet le plus rapide proposé par ce site.
Garder en note le temps et la distance annoncés par ce site.
-
-
Aller sur le site viamichelin pour effectuer la même recherche.
-
Aller sur le site openstreetmap pour effectuer la même recherche.
-
Aller sur le site Googlemap pour effectuer la même recherche.
-
-
Combien de trajets différents obtenez-vous ?
-
Pour un même trajet proposé par deux sites différents, le temps et la distance sont-ils les mêmes ?
-
Quel écart de temps entre le court et le plus long obtenu entre ces 4 sites ?
-
Algorithme de Dijkstra
Tous les sites précédents utilisent différents algorithme pour déterminer le chemin le plus court entre deux points, à partir d'une base de données.
Un des plus fameux et simple est l'algorithme de Dijkstra.
Modélisation
Tout trajet (en voiture) entre des villes peut être modélisé par un ensemble appelé graphe pondéré formé de nœuds (=points), d'arêtes (=traits) et de poids (= nombres réels positifs) :
-
les nœuds correspondent aux différentes villes possibles d'un trajet,
-
chaque arête correspond à une route possible reliant directement deux villes,
-
chaque poids d'une arête correspond à la longueur de la route modélisée par l'arête.
Voici une carte de villages proche de Vitry-le-François :
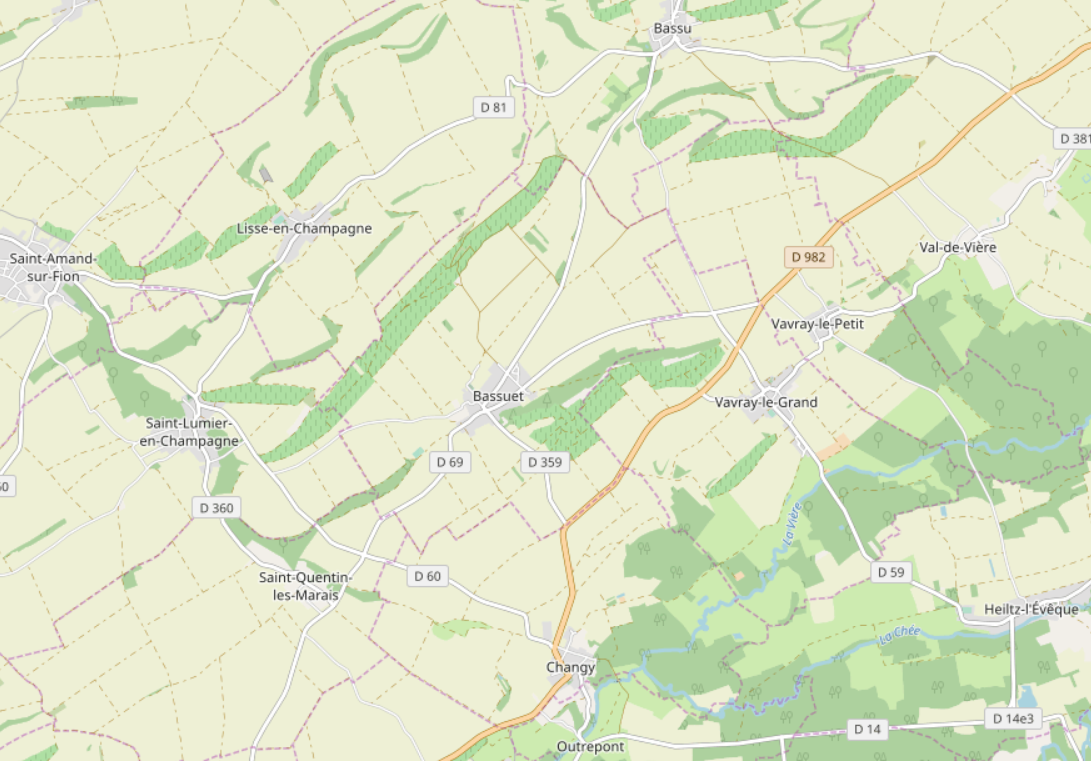
Nous ne considérons pour simplifier que les villages suivant :
-
Bassu
-
Bassuet
-
Changy
-
Heiltz-l-Évèque
-
Lisse-en-Champagne
-
Saint-Amand-sur-Fion
-
Saint-Lumier-en-Champagne
-
Vavray-le-Grand
On peut modéliser les différents villages par des nœuds et
les routes les plus courtes existantes entre deux villages par des arêtes, en y précisant leur longueur.
On obtient un graphe pondéré comme celui ci-dessous :
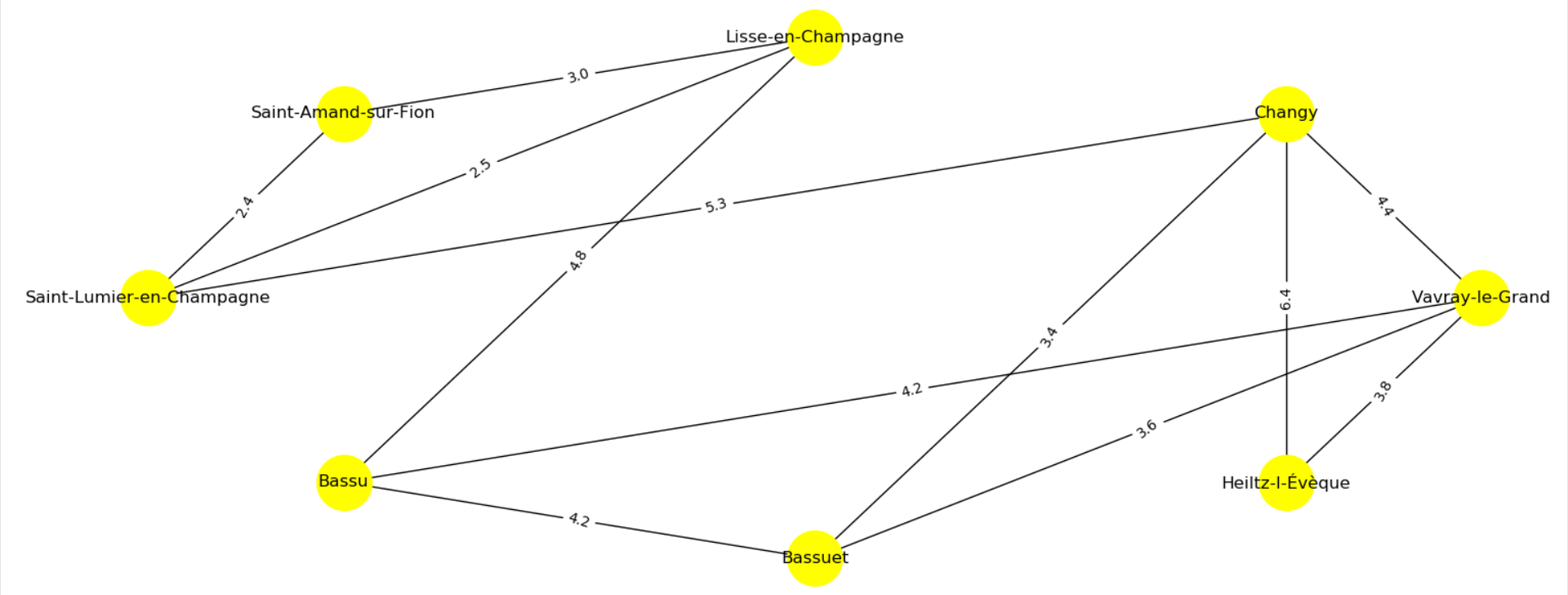
Attention ! Dans ce graphe, les positions géographiques de chaque village ne comptent plus, seules les routes directes et leur longueur sont prises en compte !
Pour simplifier les notations, une lettre est associée à chaque village :
-
(U) Bassu
-
(T) Bassuet
-
(C) Changy
-
(H) Heiltz-l-Évèque
-
(L) Lisse-en-Champagne
-
(A) Saint-Amand-sur-Fion
-
(S) Saint-Lumier-en-Champagne
-
(V) Vavray-le-Grand
D'où le graphe suivant qui est équivalent au précédent mais avec une disposition différente des villages :
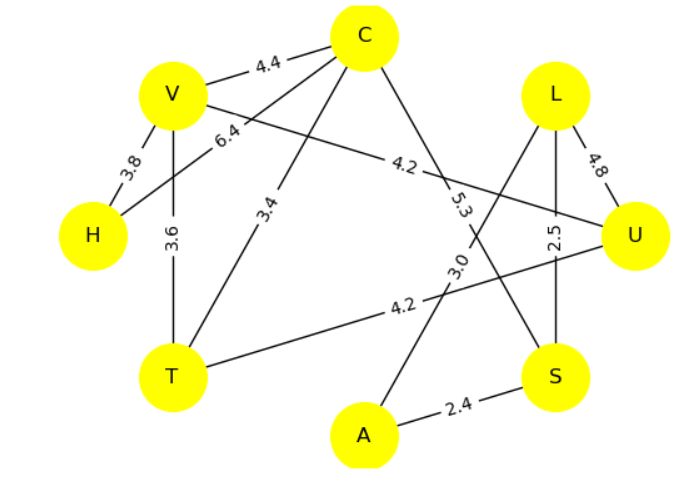
Représenter ci-dessous le graphe pondéré modélisant seulement les trajets entre les villages de :
-
(U) Bassu
-
(T) Bassuet
-
(C) Changy
-
(H) Heiltz-l-Évèque
-
(V) Vavray-le-Grand
Algorithme de Dijkstra
L'exercice de cette partie sert à découvrir l'Algorithme de Dijkstra.
Si vous avez des difficultés, n'hésitez pas à visionner la vidéo intégrée ci-dessous qui a été réalisée par Yves Monka pour son site.
Intérêt de l'algorithme de Dijkstra:
Il permet de connaître le plus court chemin entre un sommet choisi et chacun des autres sommets.
Énoncé simplifié du début de l'algorithme:
On part d'un village de départ "DEP" et on ne s'intéresse qu'aux villages directement accessibles.
Au cours de chaque itération :
-
On part du village "PP" le plus proche du point de départ non encore interdit.
-
Ce village "PP" devient interdit : on ne peut pas y retourner.
-
Dans l'ensemble des résultats, on rajoute ce village "PP" avec la distance minimale trouvée entre ce village et le village de départ "DEP".
-
Depuis ce village "PP", on regarde les villages non encore interdits et accessibles : on calcule la distance totale minimale pour rejoindre chacun de ces villages accessibles en partant au village de départ "DEP" tout en passant par le village "PP".
Le but de cet exercice est de découvrir comment fonctionne l'algorithme de Dijkstra sur le cas de l'exemple précédent ; cet algorithme va nous permettre de déterminer le chemin le plus court entre les villages de Saint-Amand-Sur-Fion (A) et Heiltz-l'Évèque (H).
Rappel du graphe permettant de visualiser les données :

Voici un tableau qui a été en partie rempli par cet algorithme de Dijkstra :

Ce tableau incomplet peut être télécharger en version .docx ou en version libre .odt.
Pour comprendre l'algorithme, regardez la vidéo proposée ci-dessus ou lisez les explications suivantes :
Ligne 1 :
On part de A, le village de départ :
La première ligne correspond aux différents sommets (= villages) du graphe.
Ligne 2 :
On part de A, le village de départ :
-
0 signifie qu'il faut au minimum 0 km pour aller de A à A,
-
- signifie que pour l'instant on ne peut pas atteindre directement les autres villages,
-
désormais la colonne A ne sera plus modifiée : on a hachuré en-dessous de 0.
Ligne 3 :
Pour la troisième ligne :
Étape 1 : on note la longueur du chemin de A à chacun des sommets adjacent non encore interdit.
-
de A à L un chemin de longueur 3 (on note 3 A pour dire qu'on arrive de A pour ce chemin court) ;
-
de A à S un chemin de longueur 2.4 (on note 2.4 A pour dire qu'on arrive de A pour ce chemin court).
Étape 2 : on garde le sommet ayant le poids le plus petit :
-
le poids le plus petit est 2.4 A,
-
on garde le sommet S et on hachure toute la colonne S en dessous de la case de 2.4 A.
Étape 3 : on garde en mémoire le village le plus proche actuellement trouvé et sa distance :
-
on reporte S (2.4 A) dans la première colonne de la ligne suivante. (ce qui signifie : "S en venant de A avec une distance totale de 2.4 km")
-
Attention le poids de S est 2.4 maintenant !
Ligne 4 :
On recommence comme pour la troisième ligne mais en partant cette fois de S avec le poids 2.4.
Étape 1 : on note la longueur du chemin de S à chacun des sommets adjacent non déjà traité (on exclut donc A et S). On ajoute la distance pour aller déjà à S. Deux cas alors :
-
Si le calcul conduit à une longueur plus petite que celle déjà obtenue, on la prend,
-
sinon, on conserve la valeur déjà trouvée. Plus précisément :
-
de S à L un chemin de longueur 2.5. donc le chemin de A à L en passant par S vaut 4.9 km (il serait noté 4.9 S). Comme c'est plus long que le chemin déjà trouvé (celui 3 A), on conserve l'ancien "3 A".
-
de S à C un chemin de longueur 5.3 donc le chemin de A à C en passant par S vaut 7.7 km. Comme c'est la seule distance connue pour l'instant, on la garde.
-
Étape 2 : on garde le sommet au poids le plus petit :
-
le poids le plus petit est 3 A,
-
on garde le sommet L et on hachure toute la colonne L en dessous de la case de 3 A.
Étape 3 : on garde en mémoire le village le plus proche actuellement trouvé et sa distance.
-
on reporte L (34 A) dans la première colonne de la ligne suivante. (ce qui signifie : "L en venant de A avec une distance totale de 34 km")
-
le poids de L est 3 maintenant.
Lignes suivantes :
Procéder de même qu'aux lignes 3 ou 4 jusqu'à ce que tous les sommets soient traités.
Recopier et compléter le tableau évoqué à l'exercice précédent, reproduit ci-dessous, en répétant la démarche expliquée dans la vidéo ci-dessus ou dans l'exercice précédent.
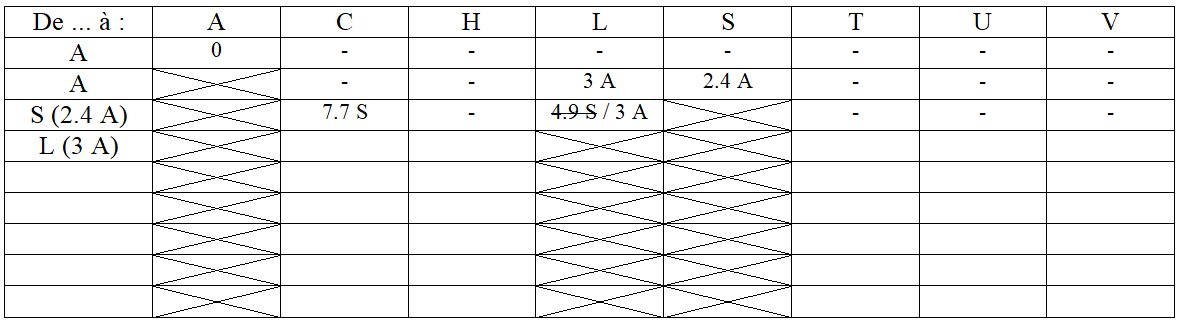
Fin de l'algorithme :
Il suffit de remonter dans le tableau à partir du sommet correspond au village visé (ici H) pour trouver le chemin (à rebours) qui part du sommet de départ (ici A).
Pour comprendre la fin de l'algorithme de Dijkstra, n'hésitez pas à regarder la vidéo proposée ci-dessus à partir de la 9ème minute.
Appliquer la fin de l'algorithme pour trouver le chemin le plus court ainsi que la distance totale pour aller de Saint-Amand-Sur-Fion (A) à Heiltz-l'Évèque (H).
Déterminer le plus cours chemins (algorithme de Dijkstra) :
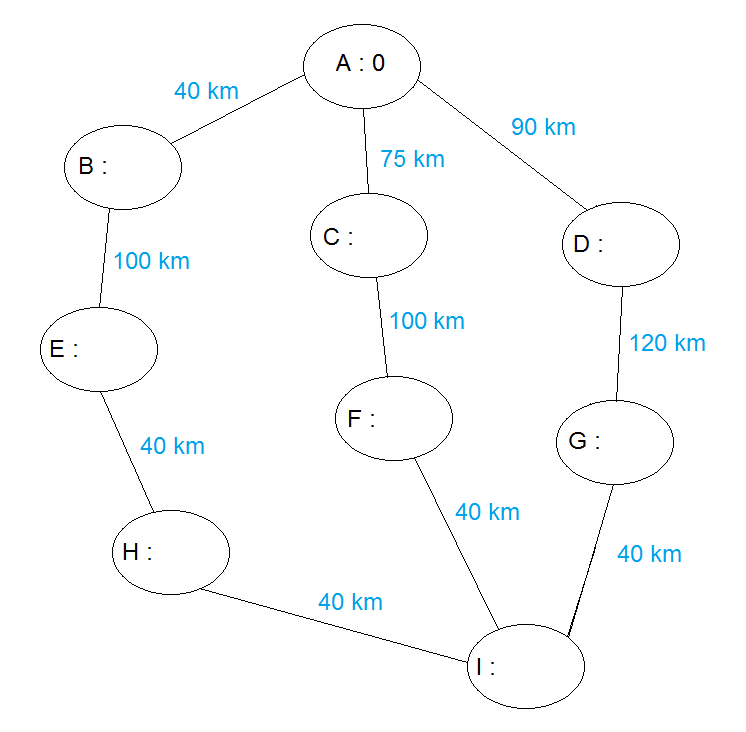
-
Quel est le chemin le plus court ?
-
Dans quel ordre ont été complétées les distances de chaque ville ?
Algorithme de Dijkstra programmé en Python
Programme Python
Dans la partie précédente, vous avez étudié à la main quel était le trajet le plus court entre les villages de Saint-Amand-Sur-Fion (A) et Heiltz-l'Évèque (H) en ne considérant que les chemins existant entre les villages suivant :
-
(U) Bassu
-
(T) Bassuet
-
(C) Changy
-
(H) Heiltz-l-Évèque
-
(L) Lisse-en-Champagne
-
(A) Saint-Amand-sur-Fion
-
(S) Saint-Lumier-en-Champagne
-
(V) Vavray-le-Grand
Vous allez désormais pouvoir vérifier votre résultat grâce à un programme en python qui :
-
modélise le problème sous forme d'un graphe,
-
affiche le graphe,
-
puis affiche le trajet le plus court entre deux villages en utilisation l'algorithme de Dijkstra.
Voici ci-dessous un programme en langage Python :
# importation des différentes bibliothèques utiles ici
import networkx as nx # pour gérer les graphes
import numpy as np
import matplotlib.pyplot as plt # pour le tracé du graphe
# création d'un graphe vide
G = nx.Graph()
# ajout au graphe des différents sommets, arêtes et des poids
G.add_edges_from([('U', 'T')], weight=4.2)
G.add_edges_from([('U', 'L')], weight=4.8)
G.add_edges_from([('U', 'V')], weight=4.2)
G.add_edges_from([('T', 'V')], weight=3.6)
G.add_edges_from([('H', 'V')], weight=3.8)
G.add_edges_from([('C', 'H')], weight=6.4)
G.add_edges_from([('T', 'C')], weight=3.4)
G.add_edges_from([('C', 'V')], weight=4.4)
G.add_edges_from([('C', 'S')], weight=5.3)
G.add_edges_from([('A', 'S')], weight=2.4)
G.add_edges_from([('A', 'L')], weight=3.0)
G.add_edges_from([('L', 'S')], weight=2.5)
# création d'un dictionnaire utilisé ensuite pour que les arêtes s'affichent avec leur poids.
edge_labels=dict([((u, v), d['weight'])
for u, v, d in G.edges(data=True)])
pos=nx.circular_layout(G)
# commande pour effacer le graphique précédent
plt.clf()
# commande pour faire des arêtes avec indication de poids
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
#commande pour tracer le graphe
nx.draw(G, pos, node_color = 'yellow', with_labels=True, node_size=1500, edge_color='black', edge_cmap=plt.cm.Reds)
plt.show()
# affichage du trajet le plus court pour le graphe G entre les deux derniers paramètres, ici 'A' et 'H'
print("Le trajet le plus court mesure",(nx.dijkstra_path_length(G, 'A', 'H')), "kilomètres.")
print("Le trajet le plus court passe par les villages successifs : ",(nx.dijkstra_path(G, 'A', 'H')))
Exécuter le script précédent sur EduPython et comparer les résultats obtenus (graphe et chemin le plus court) avec ceux obtenus précédemment.
Si votre Edupython n'est pas fonctionnel, vous pouvez utiliser capytale2 en :
-
vous connectant à ce site : https://capytale2.ac-paris.fr,
-
vous identifiant seulement grâce à l'ENT de la Région Grand-Est :

-
cliquant sur Mes activités :

-
En saisissant dans
 ce code : b4d4-3683
ce code : b4d4-3683
Normalement :
-
après un petit temps de calcul, une fenêtre avec un graphique modélisant la situation apparaît. (vous devez voir un graphe très proche de celui-ci.)
-
une fois que vous fermez la fenêtre précédente, le programme se termine en affichant la longueur du trajet le plus court, puis la liste des villages à traverser pour réaliser ce trajet le plus court.
Vous pouvez retrouver cet exercice sur capytale2 avec ce code à y saisir : b5a1-3685
Vous allez modifier le script précédent afin de l'adapter à différents changements.
-
Suite à une tempête, des arbres se sont abattus sur la route menant de Changy (C) à Heiltz-l'Évèque (H) : elle est désormais fermée. Il vous faut modifier le programme précédent afin que vous obteniez le nouveau chemin le plus court entre les villages de Saint-Amand-Sur-Fion (A) et Heiltz-l'Évèque (H)
-
Comment modifiez-vous le programme précédent pour prendre en compte la fermeture de la route mentionnée ?
-
Quel chemin obtenez-vous désormais ?
-
Quelle est la distance désormais à parcourir ?
-
Une fois à Heiltz-l'Évèque (H), vous désirez repartir vers Saint-Lumier-en-Champagne (S). Il vous faut modifier le programme précédent afin que vous obteniez le nouveau chemin le plus court entre les villages de Heiltz-l'Évèque (H) à Saint-Lumier-en-Champagne (S). (La route entre Heiltz-l'Évèque (H) et Changy (C) est toujours coupée)
-
Comment modifiez-vous le programme précédent pour cela ?
-
Quel chemin obtenez-vous désormais ?
-
Quelle est la distance désormais à parcourir ?
Application concrète
Vous pouvez retrouver cet exercice sur capytale2 avec ce code à y saisir :
- pour les élèves de M. Lourdet 4665-6691
- pour les élèves de M. Monteillet 5972-3689
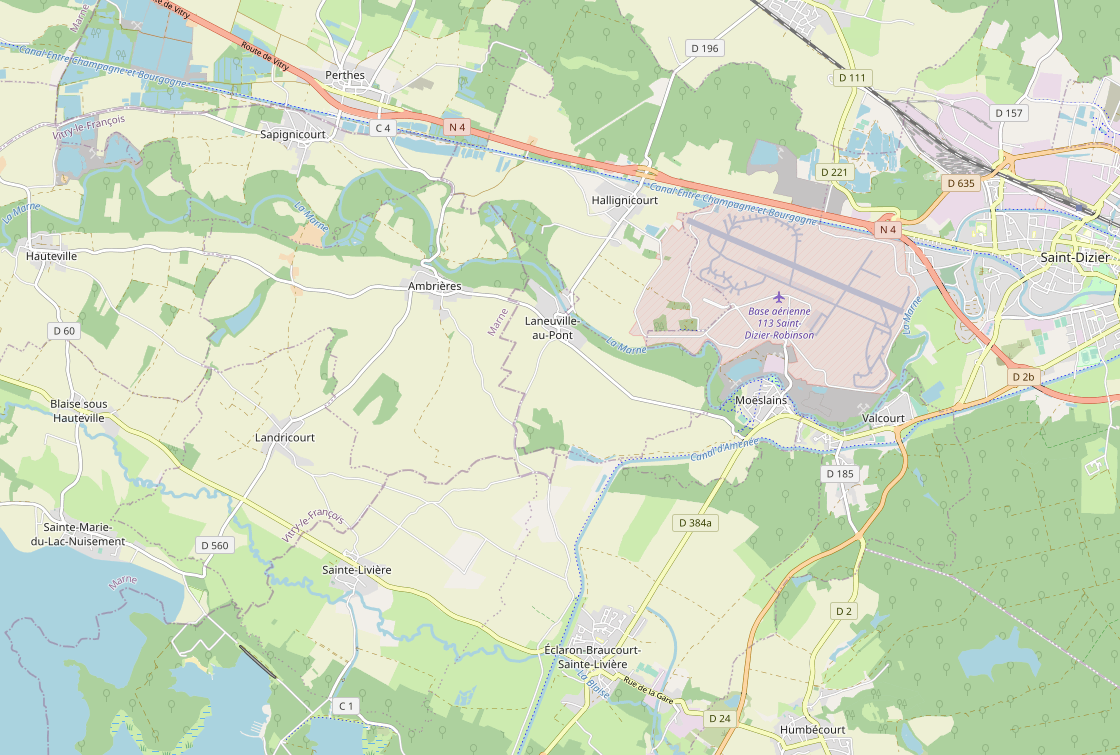
Votre meilleur ami, BGdu52, habite à Saint-Dizier. Vous avez décidé d'aller le retrouver dans sa belle ville puis qu'ensemble vous partirez en bus à la plage de Sainte Marie Du Lac, au bord du Lac du Der.
Pour la préparation de ce grand jour, vous avez pour charge de trouver le trajet de bus optimal pour vous deux. Vous avez trouvé sur Internet les informations résumées dans le tableau suivant :
Le tableau suivant donne les liaisons possibles avec leur temps de parcours et leur distances :
| Liaison | Distance | Temps |
|---|---|---|
| Saint-Dizier/Hallignicourt | 6km | 9 min |
| Hallignicourt/Ambrières | 4 km | 6 min |
| Ambrières/Landricourt | 7 km | 9 min |
| Landricourt/Sainte Marie du Lac | 8km | 14 min |
| Saint-Dizier/Valcourt | 4,5 km | 7min |
| Valcourt/Eclaron | 5 km | 7 min |
| Eclaron/Sainte-Livière | 3,5km | 4 min |
| Sainte-Livière/Sainte Marie Du lac | 8,9 km | 13 min |
| Laneuville au pont/Ambrières | 1,8 km | 2 min |
-
Vous allez reprendre le le script de l'algorithme de Dijkstra en faisant en sorte que :
-
les lettres soient remplacées par le nom des communes (par exemple, en remplaçant 'A' par "Saint-Dizier")
-
en prenant dans un premier temps comme poids d'arête les distances.
Écrire un script comme demandé ci-dessus par modification du script de l'algorithme de Dijkstra.
-
-
Lancez le script python puis vérifier que l'image du graphe obtenu est similaire à celle-ci :
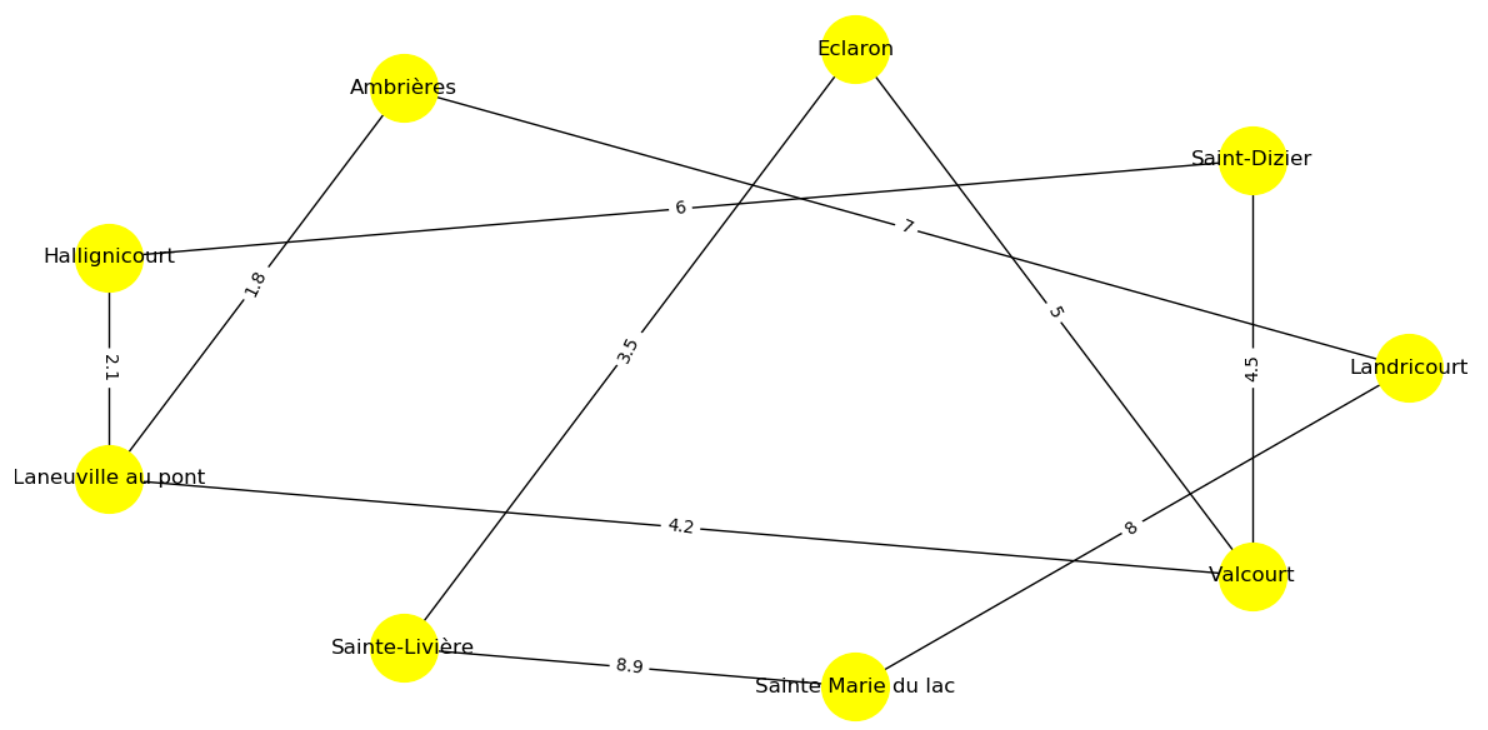
-
Quel est le trajet à effectuer en bus si l'on veut parcourir la distance la plus faible entre Saint-Dizier et Sainte Marie du Lac ? Préciser cette distance minimale.
-
Modifier le programme précédent afin de connaître le temps en bus minimal pour rejoindre Sainte Marie du Lac depuis Saint-Dizier.
Quel est le trajet de temps minimal, c'est-à-dire le plus rapide ? Quel est ce temps minimal ?
La recherche du meilleur itinéraire (en temps ou en longueur) d'un point à un autre peut être obtenue à l'aide d'algorithmes ; celui de Dijkstra en est un d'entre eux. Il fonctionne grâce à une représentation de la situation grâce à un graphe.
Escape game de moins d'une heure.
Le monde est en danger ! Seul.e.s vous pouvez peut-être le sauver !
Êtes-vous prêt.e.s à partir pour cette mission contaminante ?
Si oui, saisissez votre code secret vous permettant d'accéder aux
informations secrètes de cette nouvelle mission.
Escape game de plus d'une heure.
Une bombe a peut-être été posée ! Des vies sont sûrement en jeu !
Êtes-vous prêt.e.s à partir pour cette mission explosive ?
Si oui, saisissez votre code secret vous permettant d'accéder aux
informations secrètes de cette nouvelle mission.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International