
Parcours d'un arbre
Une implémentation possible
On décide de prendre l'implémentation des arbres donnée ci-dessous :
class Arbre:
def __init__(self, valeur):
self.v = valeur
self.fg = None
self.fd = None
def ajout_gauche(self, val):
self.fg = Arbre(val)
return self
def ajout_droit(self, val):
self.fd = Arbre(val)
return self
def affiche(self):
"""permet d'afficher un arbre"""
if self is None: # équivalent à self == None mais est plus précis (cf. remarque ci-dessous)
return None
else :
return [self.v, Arbre.affiche(self.fg), Arbre.affiche(self.fd)]
def taille(self):
if self is None:
return 0
else :
return 1 + Arbre.taille(self.fg) + Arbre.taille(self.fd)
def hauteur(self):
if self is None:
return 0
elif self.fg is None and self.fd is None:
return 0
else :
return 1 + max(Arbre.hauteur(self.fg), Arbre.hauteur(self.fd))
def get_valeur(self):
if self is None:
return None
else:
return self.v
objet == None et objet is None
sont le plus souvent équivalents.
Cependant, d'un point de vue rigueur et vitesse d'exécution a priori, il est préférable d'écrire
objet is None pour tester si l'objet considéré est vide.
Plus précisément, objet is None vérifie l'identité de l'objet
ens'assurant que la variable objet pointe vers l'unique objet
None en mémoire.
Par contre, objet == None compare les valeurs.
Si objet est une instance d'une classe où la méthode
__eq__ gérant les comparaisons a été modifiée, le résultat de
objet == None peut être différent de celui de objet is None.
Un tel exemple :
import numpy as np # bibliothèque permettant d'effectuer des calculs numériques
a = np.zeros(2) # a devient ainsi array([0., 0.]) une "matrice" ligne constituée de deux 0 (de type flottant).
print(a == None) # dans numpy, __eq__ a été modifiée pour comparer élément par élément
# Affiche [False False], ce qui n'est pas un booléen mais une "matrice" de booléens : array([False, False]).
print(a is None) # comparaison de l'identité de l'objet a avec celle l'objet None
# Affiche False.
Un autre exemple pour voir la différence entre objet1 == objet2 avec
objet1 is objet2 :
l1 = [0]
l2 = [0]
print(l1 == l2) # Affiche True car les deux listes ont le même contenu.
print(l1 is l2) # Affiche False car les deux variables l1 et l2 pointent vers des zones mémoires différentes
print(id(l1), id(l2)) # Pour visualiser les zones mémoires différentesPrise en main de l'implémentation
-
Implémenter cet arbre :
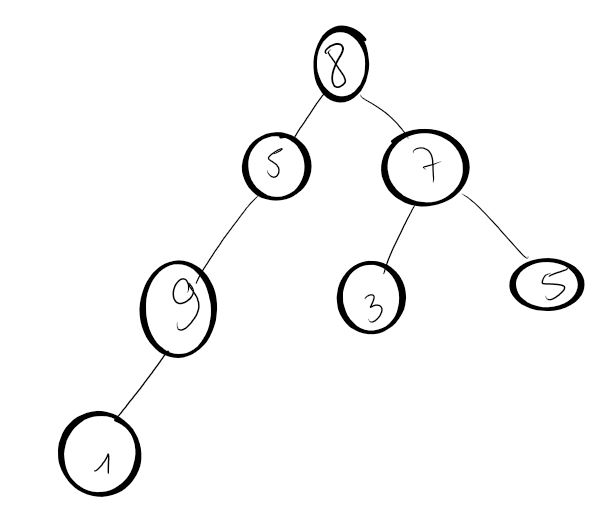
-
Tester les différentes méthodes de la classe
Arbresur l'instanciation de cet arbre.
Parcours en profondeur : infixe, préfixe et suffixe
Dans cette partie, nous allons aborder les parcours en profondeur. Il existe trois manières de parcourir un arbre en profondeur comme nous allons le voir. L'idée de ces parcours, c'est de descendre tout en bas de l'arbre avant de se déplacer vers la droite de l'arbre.
Ces parcours sont parfois notés DPS pour Depth-First Search.
Ces parcours serviront à réaliser des algorithmes de recherche textuelle par exemple ou à gérer des "AI" de jeux vidéos.
Parcours préfixe
Dans le parcours préfixe, on note tous les nœuds en commençant par la racine puis les deux sous arbres.
Réaliser à la main le parcours préfixe de cet arbre :
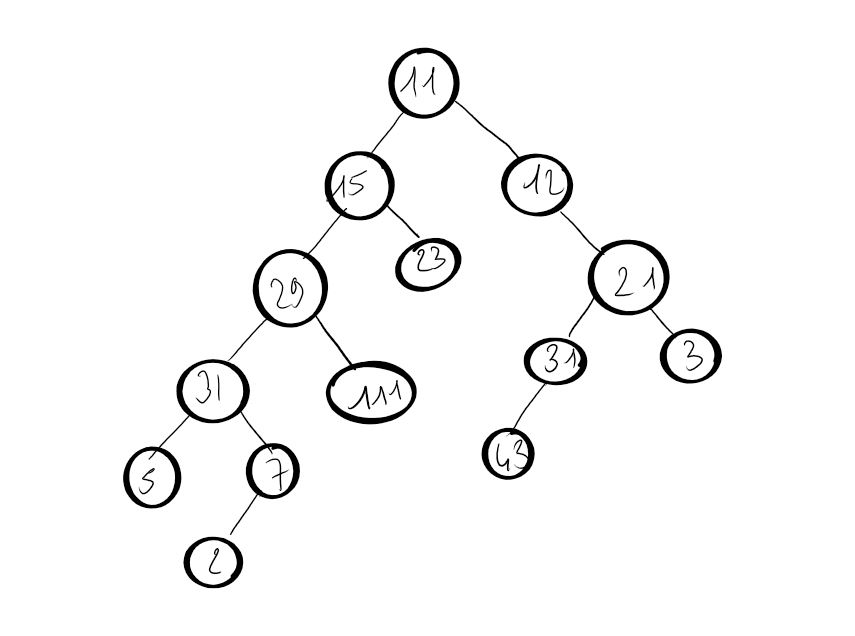
Algorithme du parcours préfixe.
Voilà la méthode écrite en Python du parcours préfixe d'un arbre.
Cette méthode fait partie de la classe Arbre (comme le prouve le début
des trois dernières lignes).
Comme les arbres ont une structure récursive, il est plus simple de l'écrire en récursif :
def dfs_prefixe(self):
if self is None:
return None
else :
Arbre.get_valeur(self) # D'abord la racine : racine en "pre"mier dans le parcours "pré"fixe
Arbre.dfs_prefixe(self.fg) # Appel récursif sous forme de fonction de la classe Arbre
Arbre.dfs_prefixe(self.fd)
Les explications :
Parcours infixe
Dans le parcours infixe, on note tous les nœuds en commençant par le sous arbre gauche puis la racine puis le sous arbre droit.
Réaliser à la main le parcours infixe de cet arbre :

Écrire l'algorithme du parcours infixe.
Parcours suffixe
Dans le parcours suffixe, on note tous les nœuds en commençant par le sous arbre gauche puis le sous arbre droit et enfin la racine .
Réaliser à la main le parcours suffixe de cet arbre :

Écrire l'algorithme du parcours suffixe.
Pour retenir le nom différent entre ces trois parcours, il suffit de retenir la position de la racine dans chaque des parcours :
-
"préfixe" : la racine est avant ses sous-arbres ; "pré" comme précéder.
-
"infixe" : la racine est entre ses sous-arbres ; "in" comme intérieur.
-
"suffixe" : la racine est après ses sous-arbres ; "su" comme succéder.
Parcours en largeur d'abord
Dans cette partie, nous allons aborder les parcours en largeur.
Ce parcours est parfois noté BFS pour Breadth-First Search.
Parcours en largeur
Lors d'un parcours en largeur d'un arbre, on note chaque sommet niveau par niveau et en commençant par la gauche.
Voici un arbre :

Le parcours en largeur de cet arbre est : $\color{orange}{8}-\color{red}{5-7}-\color{blue}{9-3-5}-\color{#00FF00}{1}$ :
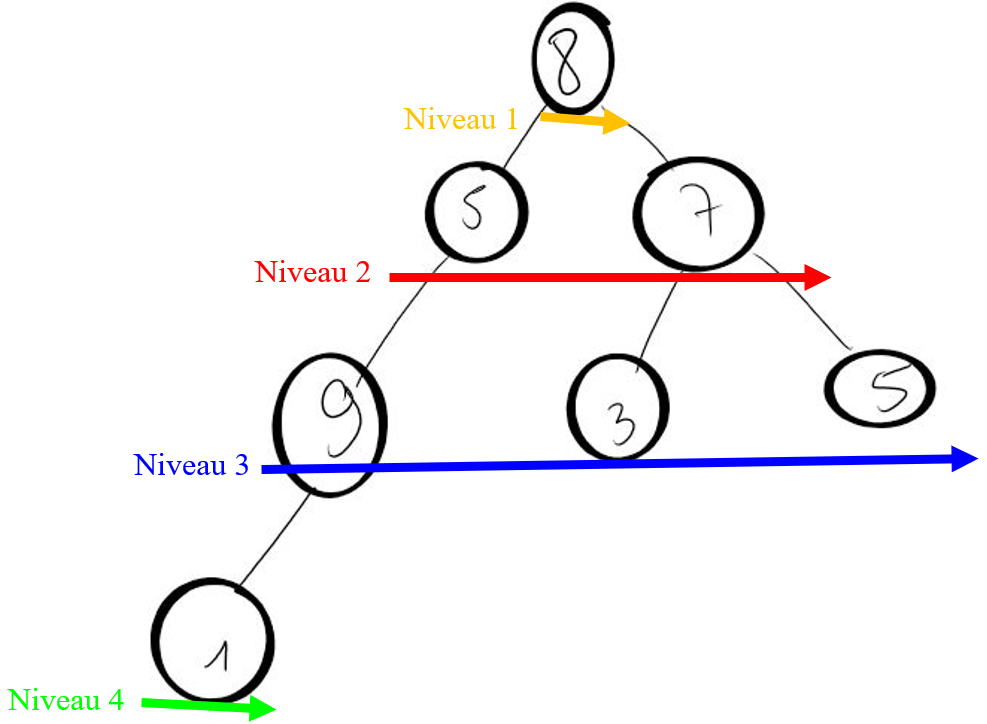
On reprend l'implémentation de file vu dans SD3.
class Element:
#chaque élément (d'une liste doublement chaînée) a pour attribut : le précédent , le suivant et la valeur de l'élément
def __init__(self, x):
self.val = x
self.precedent = None
self.suivant = None
def __str__(self): # méthode qui permet d\'afficher un tel objet grâce à un print
return str(self.val) + "<-" + str(self.suivant)l'objet file :
class File:
# ici une file est la donnée de deux attributs :
# la queue de la file de type Element
# la tête (le premier élément) de la file de type Element
# l'éventuel corps de la file sera progressivement atteinte grâce aux attributs precedent
# et suivant des objets de la classe Element sachant que :
# precedent sert à remonter vers la tête de la File
# tandis que suivant sert à descendre vers la queue de la File.
def __init__(self):
self.tete = None
self.queue = None
def enfile(self, x):
e = Element(x) # on transforme l'élément à ajouter en un objet Element de listes doublement chaînées
if self.tete is None:
self.tete = e # file initiale vide : la tete est remplacée par l'élément e
else:
e.precedent = self.queue # le précédent de l'élément pointe sur l'ancienne queue de la file
self.queue.suivant = e # l'ancienne queue de la file pointe sur e avec suivant
self.queue = e # on redéfinit self.queue par e.
def file_vide(self):
return self.tete is None #renvoie True si None et False sinon
def defile(self):
if not self.file_vide():
e = self.tete # on stocke l'élément à defiler
if e.suivant is None: # cas où il n'y a qu'un élément
self.tete = None
self.queue = None
else:
self.tete = e.suivant
self.tete.precedent = None
return e.val
def __str__(self):
return str(self.tete)
Lire le contenu de la classe File précédente et en cas d'incompréhension ou de
questions, poser des questions à votre enseignant ou
s'aider de la vidéo présente
de cet exercice du chapitre SD3.
Algorithme BFS de parcours en largeur
def BFS(arbre):
f = File()
f.enfile(arbre)
l = []
while not f.file_vide():
a = f.defile()
l.append(a.v)
if a.fg != None:
f.enfile(a.fg)
if a.fd != None:
f.enfile(a.fd)
return lTester l'algorithme sur cet arbre :

Le précédent algorithme BFS de parcours en largeur consiste à chaque Nœud étudié de noter sa valeur puis de mettre en mémoire le fait qu'il faudra visiter ses enfants après les nœuds qu'il était déjà prévu de visiter : d'où l'utilisation d'une file de mémorisation pour un parcours en largeur.
Algorithmes des arbres binaires de recherche
Une implémentation possible
Voila l'implémentation des arbres binaires de recherche que nous avons vu dans sd4 :
class ABR:
def __init__(self, valeur, fg=None, fd=None):
self.v = valeur
self.fg = fg
self.fd = fd
def ajoute(self, valeur):
if self is None:
return ABR(valeur, None, None)
elif valeur < self.v:
return ABR(self.v, ABR.ajoute(self.fg, valeur), self.fd)
else:
return ABR(self.v, self.fg, ABR.ajoute(self.fd, valeur))
def affiche(self):
if self is None:
return None
else :
return [self.v, ABR.affiche(self.fg), ABR.affiche(self.fd)]Implémenter l'arbre suivant :
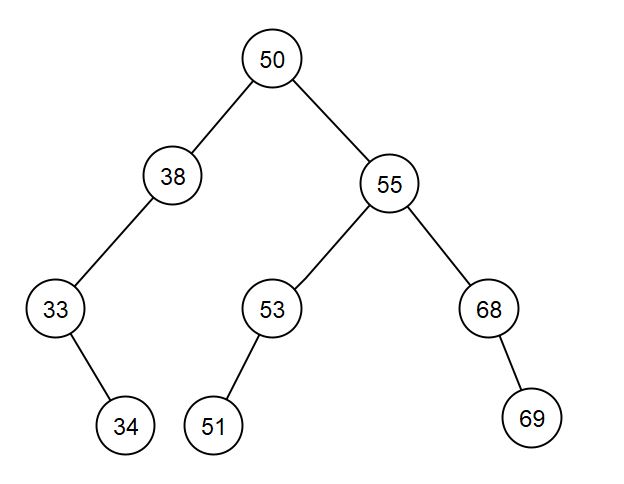
Recherche d'une clé
Écrire la méthode recherche(self, val) qui renvoie True si val est une clé de
l'arbre et False sinon.
Le principe ici est celui de la dichotomie. On élimine grâce à la structure des arbres binaires de recherche la moitié des nœuds restant à chaque étape.
Insérer une clé
La méthode qui insère un élément dans un arbre binaire de recherche est déjà écrite. Quelle est-elle ?
Commenter cette méthode.
Exercices
Écrire une méthode min(self) qui renvoie la clé minimale d'un arbre binaire de recherche.
Écrire une méthode max(self) qui renvoie la clé maximale d'un arbre binaire de recherche.
Donner tous les arbres binaires de recherche formés des trois nœuds : 7, 52, 40
Écrire une fonction listeEnArbre(l) qui en paramètre reçoit une liste d'entiers et qui renvoie
un arbre binaire de recherche contenant les éléments de la liste l.
Exercices issus du Bac
Cet exercice reprend la seule question du sujet de bac non traitée dans le sujet déjà commencé dans SD4.
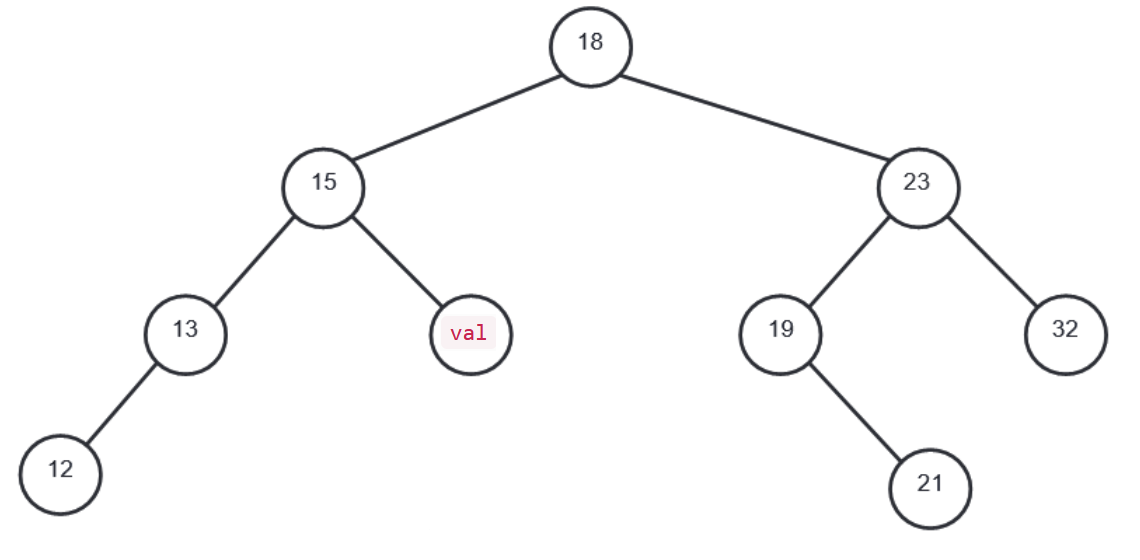
On considère l'arbre binaire de recherche représenté ci-dessous, où val représente l'entier 16 :
On rappelle qu’un parcours infixe depuis un nœud consiste, dans l’ordre, à faire un parcours
infixe sur le sous arbre-gauche, afficher le nœud puis faire un parcours infixe sur le sous-arbre
droit.
Dans le cas d’un parcours suffixe, on fait un parcours suffixe sur le sous-arbre gauche puis un
parcours suffixe sur le sous-arbre droit, avant d’afficher le nœud.
-
Donner les valeurs d’affichage des nœuds dans le cas du parcours infixe de l’arbre.
-
Donner les valeurs d’affichage des nœuds dans le cas du parcours suffixe de l’arbre.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International