Discriminant
Calculer le discriminent des polynômes suivants :
- $X^2-3X+2$
- $-X^2-5$
- $X-2-X^2$
- $X-1$
- $\Delta=(-3)^2-4\times 2\times 1=1$
- $\Delta=0^2-4\times (-1) \times (-5)=-20$
- $\Delta = 1^2-4\times (-1)\times(-2)=-7$
- Ce polynôme n'est pas de degré 2
Dérivation
Dériver la fonction suivante : $$f:x\longmapsto \frac{x^2-1}{x+2}$$
$f$ est un fonction définie est dérivable sur $\mathbb{R}\backslash\{-2\}$.
Soit $x\in\mathbb{R}\backslash\{-2\}$, $f'(x)=\frac{(2x)(x+2)-(1)(x^2-1)}{(x+2)^2}=\frac{x^2+4x+1}{(x+2)^2}$
Variation de suite
Soit $(u_n)_{n\in\mathbb{N}}$ telle que $\left \{ \begin{array}{l } u_{n+1} = u_n+2n+1 \\ u_0 = -4 \\ \end{array} \right.$
Étudier les variations de $u$.
Soit $n\in\mathbb{N}$, $u_{n+1}-u_{n}=u_n+2n+1-u_n=2n+1>0$(puisque $n\geq0$) donc $u$ est strictement croissante.
algorithme de type "seuil"- Tant que
Une balle part d'une hauteur de $2,5$ m et perd $15\%$ de sa hauteur à chaque rebond. On cherche le nombre de rebonds pour qu'elle perde la moitié de sa hauteur.
Proposer un algorithme qui résout ce problème et en faire usage pour y répondre.
- $h\leftarrow 2,5$
- $n\leftarrow 0$ Tant que $h>1,25$
- $\hspace{0.5cm}$ $n\leftarrow n+1$
- $\hspace{0.5cm}$ $h\leftarrow 0,85h$
- Fin tant que
Suite arithmético-géométrique
Soit $(u_n)_{n\in\mathbb{N}}$ telle que $\left \{ \begin{array}{c} u_{n+1} = 2u_n-1 \\ u_0 = 2 \\ \end{array} \right.$
Soit $(v_n)_{n\in\mathbb{N}}$ telle que $v_n=u_n-1$, $n\in\mathbb{N}$.
Montrer que $v$ est géométrique. En déduire que une expression de $v$ en fonction de $n$ puis de $u$.
Quelle la limite de $u$?
Soit $n\in\mathbb{N}$, $v_{n+1}=u_{n+1}-1=2u_n-1-1=2u_n-2=2(u_n-1)=2v_n$ donc $v$ est la suite géométrique de raison 2 et de premier terme $v_0=u_0-1=1$.
$v_n=2^n$, $n\in\mathbb{N}$.
$2>1$ donc $\lim\limits_{n \to +\infty} 2^n=+\infty$, $u$ diverge et $\lim\limits_{n \to +\infty} u_n=+\infty$.
Manipulation d'un trinôme
Déterminer les racines, le signe, une factorisation et les variations de la fonction polynomiale $f$ définie sur $\mathbb{R}$ par $f(x)=-2x^2+4x+1$.
$\Delta=24>0$
Les racines sont $x_1=\frac{-4+\sqrt{24}}{-4}=1-\frac{\sqrt{6}}{2}$ et $x_2=1+\frac{\sqrt{6}}{2}$.
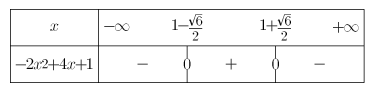
$f(x)>0$ pour $x\in]1-\frac{\sqrt{6}}{2};1+\frac{\sqrt{6}}{2}[$
$f(x)<0$ pour $x\in]-\infty;1-\frac{\sqrt{6}}{2}[\cup]1+\frac{\sqrt{6}}{2};+\infty[$.
$-\frac{b}{2a}=1$ et $a<0$ donc $f$ est strictement croissante sur $]-\infty;1[$ et strictement décroissante sur $1;+\infty[$
$-2x^2+4x+1=-2(x-(1+\frac{\sqrt{6}}{2}))(x-(1+\frac{\sqrt{6}}{2}))$
la preuve d'une égalité avec un raisonnement par récurrence
Soit $u$ une suite définie par $u_0=2$ et $u_{n+1}=\frac{u_n}{1+u_n}$.
Démontrer que pour tout $n\in \mathbb{N}$, $$u_n=\frac{2}{2n+1}.$$
On définit, pour tout $n\in\mathbb{N}$, $P(n):"u_n=\frac{2}{2n+1}"$.
Initialisation : $n=0$
$u_0=2$ et $\frac{2}{2\times 0+1}= 2$ donc P(0) est vraie
Hérédité : Soit $p\in\mathbb{N}$ supposons $P(p)$ vraie.
D'après $P(p)$ on a $u_p=\frac{2}{2p+1}$.
$u_{p+1}=\frac{u_p}{1+u_p}=\frac{\frac{2}{2p+1}}{1+\frac{2}{2p+1}}= \frac{\frac{2}{2p+1}}{\frac{2p+1}{2p+1}+\frac{2}{2p+1}}= \frac{\frac{2}{2p+1}}{\frac{2p+1+2}{2p+1}}=\frac{2}{2p+1}\times\frac{2p+1}{2p+3}=\frac{2}{2p+3}=\frac{2}{2(p+1)+1}$ Ainsi $P(p+1)$ est vraie.
Le principe de récurrence montre que pour tout $n\in\mathbb{N}$, $u_n=\frac{2}{2n+1}$.
suite géométrique
Soit $u$ une suite géométrique de raison -3 et de premier terme $u_0=5$.
- Exprimer $u_{n+1}$ en fonction de $u_n$, pour tout $n\in\mathbb{N}$.
- Exprimer $u_n$ en fonction de $n$, pour tout $n\in\mathbb{N}$.
- Calculer $u_2+u_3+...+u_{35}$.
- $u_n=u_p\times q^{n-p}$.
- $u_p+u_{p+1}+...+u_n=u_p\frac{1-q^{n-p+1}}{1-q}$
- $u_{n+1}=-3u_n$, pour tout $n\in\mathbb{N}$.
- $u_n=5(-3)^n$, pour tout $n\in\mathbb{N}$.
- $u_2+u_3+...+u_{35}=u_2\frac{1-(-3)^{34}}{1-(-3)}=\frac{45}{4}(1-(-3)^{34})$.
suite arithmétique
Soit $u$ une suite arithmétique de raison -3 et de premier terme $u_0=5$.
- Exprimer $u_{n+1}$ en fonction de $u_n$, pour tout $n\in\mathbb{N}$.
- Exprimer $u_n$ en fonction de $n$, pour tout $n\in\mathbb{N}$.
- Calculer $u_2+u_3+...+u_{35}$.
- $u_n=u_0+nr$; $u_n=u_1+(n-1)r$ ;$u_n=u_p+(n-p)r$
- $u_p+...+u_n=\frac{(n-p+1)(u_p+u_n)}{2}$ pour tout p et n entier avec $p\leq q$
- $u_{n+1}=u_n-3$, pour tout $n\in\mathbb{N}$.
- $u_n=5-3n$, pour tout $n\in\mathbb{N}$.
- $u_2+u_3+...+u_{35}=\frac{(35-2+1)(u_2+u_{35})}{2}=\frac{34(5-3\times2+5-3\times35)}{2}=-1717$.
la simplification d'une fraction/puissances
Simplifier les expressions suivantes :
- $\frac{3}{1-\frac{x+1}{x-1}}$.
- $\frac{4^2\times2^3}{2^{-3}}$.
- $a^n\times a^m=a^{n+m}$
- $\frac{a^n}{a^m}=a^{n-m}$
- $(a^n)^m=a^{n\times m}$
- $a^n\times b^n=(ab)^n$
- $\frac{a^n}{b^n}=(\frac{a}{b})^n$
- $\frac{1}{a^n}=a^{-n}$
- $a^0=1$
- $\frac{3}{1-\frac{x+1}{x-1}}=\frac{3}{\frac{x-1}{x-1}-\frac{x+1}{x-1}}=\frac{3}{\frac{x-1-x-1}{x-1}}=\frac{3}{\frac{-2}{x-1}}=-\frac32(x-1)$.
- $\frac{4^2\times2^3}{2^{-3}}=\frac{2^{2^2}\times2^3}{2^{-3}}=2^4\times 2^{3}\times2^3=2^{10}$.
la simplification d'une fraction/puissances
Simplifier les expressions suivantes :
- $\frac{x+1}{1-\frac{x+1}{x-1}}-1$.
- $\frac{4^n2^n}{2^{-n}}\frac{3^n 2^{n+2}}{6^{-n+1}}$.
- $\frac{x+1}{1-\frac{x+1}{x-1}}-1=\frac{x+1}{\frac{x-1}{x-1}-\frac{x+1}{x-1}}-1=\frac{x+1}{\frac{-2}{x-1}}-1=-\frac{(x+1)(x-1)}2-1=-\frac{x^2-1}{2}-\frac22=-\frac{x^2+1}{2}$
- $\frac{4^n2^n}{2^{-n}}\frac{3^n 2^{n+2}}{6^{-n+1}}=(2^2)^n2^{2n}\frac{3^n2^{n+2}}{3^{-n+1}2^{-n+1}}=2^{4n}3^{2n-1}2^{2n+1}=2^{6n+1}3^{2n-1}$.
le calcul de dérivée
Dériver les fonctions suivantes :
- $f(x)=(2x+3)^3$
- $g(x)=\sqrt{2x+4}$.
- $h(x)=\cos(4x+1)$
Formule
- $(u^{\alpha})'=\alpha u'u^{\alpha-1}$
- $(\sqrt{u})'=\frac{u'}{2\sqrt{u}}$
- $(\cos(u))'=-u'\sin(u)$
- $f'(x)=3\times2\times(2x+3)^2=6(2x+3)^2$
- $g'(x)=\frac{2}{2\sqrt{2x+4}}=\frac1{\sqrt{2x+4}}$
- $h'(x)=-4\sin(4x+1)$
la preuve de la croissance d'une suite avec un raisonnement par récurrence
Soit $(u_n)_{n\in\mathbb{N}}$ telle que :
$\left \{ \begin{array}{l} u_{n+1} =\sqrt{2u_n+3}\\ u_0 = 0 \\ \end{array} \right.$
Prouver par récurrence que $u$ est croissante.
On définit, pour tout $n\in\mathbb{N}$, $P(n):"u_{n+1}>u_n"$.
Initialisation : $n=0$
$u_0=0$, $u_1=\sqrt{2u_0+3}=\sqrt{3}$.
On a bien $u_1>u_0$ donc $P(0)$ est vraie.
Hérédité :
Soit $p\in\mathbb{N}$ supposons $P(p)$ vraie.
D'après $P(p)$ on a $u_{p+1}>u_p$ $Longrightarrow$ $ $2u_{p+1}>2u_{p}$ $Longrightarrow$ $2u_{p+1}+3>2u_{p}+3$ $Longrightarrow$ $\sqrt{2u_{p+1}+3}>\sqrt{2u_{p}+3}$ $Longrightarrow$ $u_{p+2}>u_{p+1}$. Ainsi $P(p+1)$ est vraie.
Le principe de récurrence montre que pour tout $n\in\N$, $u_{n+1}>u_n$.
Détermination de la position relative de fonctions
Soit $f:x\longmapsto\frac{x-1}{x+2}$ définie sur $\mathbb{R}\backslash\{-2\}$ par $g:x\longmapsto x-1$ définie sur $\mathbb{R}$.
Étudier la position relative des courbes représentatives de $f$ et de $g$.
Soit $x\in\mathbb{R}\backslash\{-2\}$, $f(x)-g(x)=\frac{x-1}{x+2}-(x-1)=\frac{x-1}{x+2}-\frac{(x-1)(x+2)}{x+2}=\frac{x-1-(x^2+x-2)}{x+2}=\frac{-x^2+1}{x+2}=\frac{(1-x)(1+x)}{x+2}$
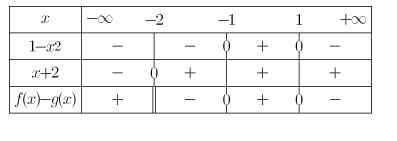
Ainsi la courbe représentative de $f$ est au dessus de celle de $g$ sur $]-\infty;-2[\cup]-1;1[$ et est en dessous sur $]-2;-1[\cup ]1;+\infty[$.
limite de suite
- $\lim\limits_{n \to +\infty} n^5-3n^3+2n+1$
- $\lim\limits_{n \to +\infty} \frac{-n^2+1}{2-n}$
- $\lim\limits_{n \to +\infty} n^5-3n^3+2n+1=\lim\limits_{n\to +\infty} n^5(1-\frac{3}{n^2}+\frac{2}{n^4}+\frac{1}{n^5})=+\infty$
- $\lim\limits_{n \to +\infty} \frac{-n^2+1}{2-n}=\lim\limits_{n \to +\infty} \frac{n^2(-1+\frac{1}{n^2})}{n(\frac{2}{n}-1)}=\lim\limits_{n \to +\infty} n\frac{-1+\frac{1}{n^2}}{\frac{2}{n}-1}=+\infty$
Poucentage
- Alphonse Danlmur dispose de 2000 euros, il veut donner $15\%$ a une association. Combien donne-t-il?
- Amour Hire De Rire dispose de 1500 euros, il les place à un taux annuel de $3\%$. Combien a-t-il à la fin de la deuxième année.
- Charles Ottofraize dispose de 180 euros. On lui donne 50 euros. De quel pourcentage a augmenté son capital?
- $0.15\times 2000=300$
- $1500\times (1+\frac{3}{100})(1+\frac{3}{100})$
- $180+50=230$, $\frac{230}{180}=1,28$ à $10^{-2}$ près. Le pourcentage d'augmentation est de $28\%$ à l'unité près.
technique de base
- Développer : $-3(5\times 3^{n-2}+5\times 3-n+5)$
- Déterminer le signe de : $2^n-2^{n+1}+2^{n+2}$, $n\in\mathbb{N}$
- $-3(5\times 3^{n-2}+5\times 3-n+5)=-5\times 3^{n-1}-45+3n-15=-5\times 3^{n-1}-60+3n$
- $2^n-2^{n+1}+2^{n+2}=2^n(1-2+2^2)=2^n(3)>0$
technique de base : suite
- On donne $P(n):"u_{n+1}=5u_n+n-5"$. Écrire $P(n+1)$
- On donne $u_n=3^n+5n-2$. Calculer $u_{n+1}-u_n$. En déduire les variations de la suite.
- $P(n+1):"u_{n+2}=5u_{n+1}+n+1-5"$
- $u_{n+1}-u_n=3^{n+1}+5(n+1)-2-(3^n+5n-2)=3^{n+1}-3^n+5=3^n(3-1)+5=2(3^n)+5>0$. Donc $u$ est croissante.
Formule des probabilité conditionnelle
On donne $P(A)=0,3$, $P(B)=0,2$ et $P(A\cup B)=0,3$. Calculer $P_A(B)$.
Arbre
La proportion de droitiers est de $0,85$. Les droitiers sont créatifs selon la proportion de $0,4$. Les gauchers sont créatifs selon la proportion de $0,7$.
Faire un arbre et trouver la probabilité d'être droitier sachant que la personne est créative.
On note $C$ l'événement "l'individu est créatif" et $D$ l'événement "l'individu est droitier".
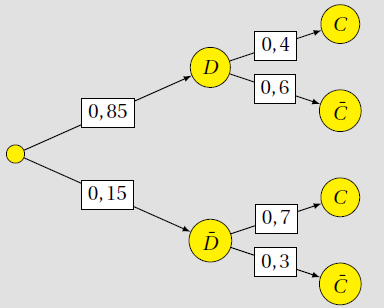
La formule des probabilités totales montre que $P(C)=P(C\cap D)+P(C\cap \bar{D})=P(D)P_D(C)+P(\bar{D})P_{\bar{D}}(C)=0,85\times 0,4+0,15\times 0,7=0,445$
$P_C(D)=\frac{P(D\cap C)}{P(C)}=\frac{0,85\times 0,4}{0,445}=0,76$.
Arbre2
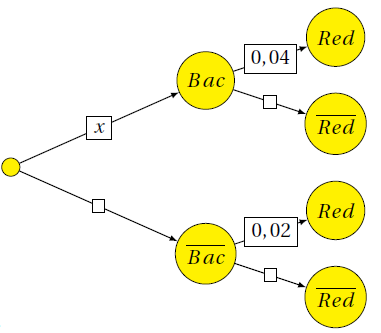
On donne $P(Red)=0,035$. Calculer $x$.
La formule des probabilités totales montre que :
$$P(Red)=0,035=P(Bac)P_{Bac}(Red)+P(\overline{Bac})P_{\overline{Bac}}(\overline{Red})=x0,04+(1-x)0,02$$ D'où $x=0,75$.
Egalité, implication et équivalence.
Compléter par $=$ ou $\Rightarrow$ ou $\Leftrightarrow$
- ABC rectangle en A ... $BC^2=AB^2+AC^2$
- $x+1=0$ ... $x=-1$
- $x=1$ ... $x^2=1$
- $c(ak+bk)$ ... $cak+cbk$...$k(ca+cb)$
- $2$ ...$3-1$
- $f'(x)$ est strictment négatif sur l'intervalle $I$ ... $f$ est strictement croissante sur l'intervalle $I$.
- $x\geq0$ ... $\sqrt{x^2}=x$
- $a$ est un entier naturel ... $a\geq0$
- ABC rectangle en A $\Leftrightarrow$ $BC^2=AB^2+AC^2$
- $x+1=0$ $\Leftrightarrow$ $x=-1$
- $x=1$ $\Rightarrow$ $x^2=1$
- $c(ak+bk)$ =$cak+cbk$=$k(ca+cb)$
- $2$ =$3-1$
- $f'(x)$ est strictment négatif sur l'intervalle $I$ $\Leftrightarrow$ $f$ est strictement croissante sur l'intervalle $I$.
- $x\geq0$ $\Leftrightarrow$ $\sqrt{x^2}=x$
- $a$ est un entier naturel $\Rightarrow$ $a\geq0$
Vrai ou Faux ?
Compléter par $=$ ou $\Rightarrow$ ou $\Leftrightarrow$
- $\sqrt{3^2+5^2}=8$
- $\sqrt{(-2)^2}=-2$
- $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$
- $\sqrt{(x+1)^2}=x+1$
- $\sqrt{ab}=\sqrt{a}\sqrt{b}$
- $\sqrt{3^2+5^2}=8$ Faux !!!!!!!!!!! $\sqrt{a+b}\ne \sqrt{a}+\sqrt{b}$ $\sqrt{(-2)^2}=-2$ Faux !!!!!!!!!!! $=2$
- $\sqrt{ab}=\sqrt{a}\sqrt{b}$Faux !!!!!!!!!!! si a et b sont négatifs leurs racines carrées n'ont pas de sens.
- $\frac{1}{sqrt{2}}=\frac{1\times \sqrt{2}}{\sqrt{2}\sqrt{2}}=\frac{\sqrt{2}}{2}$ Vrai !
- $\sqrt{(x+1)^2}=x+1$ Faux !!!!!!! il faut que $x+1\geq 0$ pour que ce soit vrai. En fait on a $\sqrt{(x+1)^2}=|x+1|$
Loi binomiale
Soit $X$ une v.a. qui suit une loi binomiale de paramètres $\mathcal{B}(15;0,3)$.
Calculer $P(X\leq 4)$; $P(X=7)$; $P(X>5)$ et $P(2<X<5)$
- $P(X\leq 4)=0,52$
- $P(X=7)=0,08$
- $P(X>5)=1-P(X\leq 5)=0,28$
- $P(2<X<5)=P(X\leq4)-P(X\leq 1)=0,52-0,04=0,48$
Technique de calcul
Résoudre sur $\mathbb{R}\backslash\{-1\}$, $$\frac{3x+5}{x+1}\leq x+5$$
Soit $x\in\mathbb{R}\backslash\{-1\}$, $\frac{3x+5}{x+1}\leq x+5$ $\Leftrightarrow$ $\frac{3x+5}{x+1}-(x+5)\leq 0$ $\Leftrightarrow$ $\frac{3x+5-(x+5)(x+1)}{x+1}\leq 0$ $\Leftrightarrow$ $\frac{-x^2-3x}{x+1}\leq 0$ $\Leftarrow$ $\frac{x(-x-3)}{x+1}\leq 0$
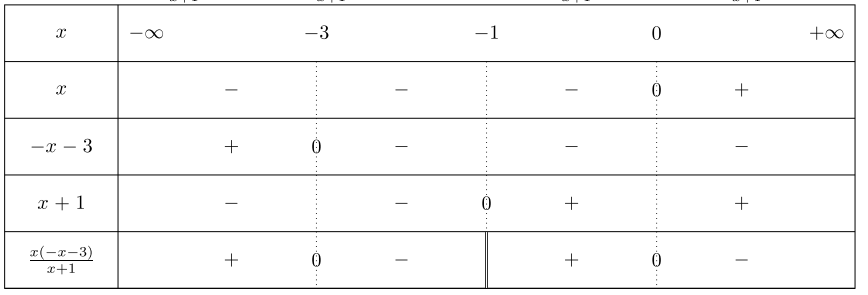
L'ensemble solution est $[-3;-1[\cup ]0;+\infty[$
Technique de calcul en Physique
On rappelle que dans un circuit électrique $U=R\times I$ ( loi d'Ohm )
- Si $I=20mA$ et $R=100 \Omega$, donner la tension.
- Si $U=5V$ et $R=100 \Omega$, donner l'intensité.
- Si $I=20mA$ et $U=3.3V$, donner la résistance.
- $U=20*100=2000 mV=2V$
- $I=\frac{U}{R}=\frac{5}{100}=0.05A=50mA$
- $R=\frac{3,3}{0,02}=165\Omega$
Corollaire du TVI
Combien l'équation $x^3+x=1$ admet-elle de solutions dans $\mathbb{R}$?
$f:\longmapsto x^3+x$ est une fonction continue sur $\R$ en tant que fonction polynomiale.
$f'(x)=3x^2+1>0$, $x\in\mathbb{R}$. $f$ est donc strictement croissante sur $\mathbb{R}$.
De plus $\lim\limits_{x\to -\infty}f(x)=\lim\limits_{x\to-\infty}x^3=-\infty$ et $\lim\limits_{x\to +\infty}f(x)=\lim\limits_{x\to+\infty}x^3=+\infty$.
Or $1\in]-\infty;+\infty[$. D'après le corollaire du théorème du TVI, $f(x)=1$ admet une unique solution $\mathbb{R}$.
Déterminer la forme algébrique
Déterminer la forme algébrique de $$\frac{3+2i}{4-2i}.$$
$\frac{3+2i}{4-2i}=\frac{(3+2i)(4+2i)}{(4-2i)(4+2i)}=\frac{12-4+6i+8i}{16+4}=\frac{8+14i}{20}=\frac{2}{5}+\frac{7}{10}i.$
Déterminer la forme algébrique
On considère la transformation complexe : $$Z=\frac{z}{\bar{z}}\textrm{, avec } z\neq0$$ Écrire $Z$ sous forme algébrique.
$Z=\frac{z}{\bar{z}}=\frac{x+iy}{x-iy}=\frac{(x+iy)(x+iy)}{(x-iy)(x+iy)}=\frac{x^2-y^2-2ixy}{x^2+y^2}=\frac{x^2-y^2}{x^2+y^2}+i\frac{2xy}{x^2+y^2}$
Equation cartésienne de cercle
Soit $A$ d'affixe $1-i$. Déterminer l'équation cartésienne du cercle $\Gamma$ de centre $A$ et de rayon 2
$M(x;y)\in\mathcal{C}(\Omega,r)$ $\Longleftrightarrow$ $\Omega M=r$ $\Longleftrightarrow$ $(x-x_{\Omega})^2+(y-y_{\Omega})^2=r^2$
Cette dernière équation est appelée équation cartésienne de $\mathcal{C}$.
Soit $M(x;y)$ un point du plan.
$M\in\Gamma$ $\Longleftrightarrow$ $AM=2$ $\Longleftrightarrow$ $(x-1)^2+(y+1)^2=2^2$ $\Longleftrightarrow$ $x^2-2x+y^2+2y-2=0$
Equation cartésienne de cercle 2
Déterminer les caractéristiques des ensembles de points définis par les équations cartésiennes suivantes :
- $\{M(x;y)$ tel que $x^2+2x+y^2-4y+2=0\}$
- $\{M(x;y)$ tel que $x^2+6x+y^2-1=0\}$
- $\{M(x;y)$ tel que $x^2+x+y^2-4y-4=0\}$
- $x^2+2x+y^2-4y+2=0$ $\Longleftrightarrow$ $(x+1)^2-1+(y-2)^2-4+2=0$ $\Longleftrightarrow$ $(x+1)^2+(y-2)^2=3$. L'ensemble cherché est le cercle de centre le point d'affixe $-1+2i$ et de rayon $\sqrt{3}$.
- $x^2+6x+y^2-1=0$ $\Longleftrightarrow$ $(x+3)^2-9+y^2-1=0$ $\Longleftrightarrow$ $(x+3)^2+y^2=10$. L'ensemble cherché est le cercle de centre le point d'affixe $-3$ et de rayon $\sqrt{10}$.
- $x^2+x+y^2-4y-4=0$ $\Longleftrightarrow$ $(x+\frac12)^2-\frac14+(y-2)^2-4-4=0$ $\Longleftrightarrow$ $(x+\frac12)^2+(y-2)^2=\frac{33}{4}$. L'ensemble cherché est le cercle de centre le point d'affixe $-\frac12+2i$ et de rayon $\sqrt{\frac{33}{4}}$.