1. La correction de tous les exercices (même les deux derniers) est accessible avec ce code : Qu'on_court!Pret=>pars_a_Sion
    Ce code est à saisir n'importe quelle zone de saisie , comme par exemple celle ci-dessous :

    Code de déblocage de la correction :

  2. Il est aussi possible de débloquer toutes les aides progressives vues durant la séance pour réussir la plupart des exercices avec ce code Z.
    Ce code est à saisir dans n'importe quelle zone de saisie , comme par exemple celle ci-dessous :

Logique et raisonnements

Logique

Une proposition mathématique est un énoncé qui est soit vraie, soit fausse (mais pas les deux en même temps).
Cette proposition peut dépendre d'une variable ($x$, $n$, ...).

Parmi les énoncés suivants, cocher ceux qui correspondent à une proposition mathématique :

1532 est une nombre pair.
Il existe un réel $x$ tel que $x^2=-1$.
$e^{-x}\times (x+1)$.
$x^2 \ge 4$.
Pour tous les réels $x$ il existe un entier relatif $n$ tels que $n\le x\lt n+1$.

Une fois les propositions mathématiques reconnues cochées, vérifier vos réponses en cliquant sur ce bouton :

Voici les deux quantificateurs à connaître :

La proposition "$\exists x\in \mathbb{R}\ x^2=4$" est vraie : $x=2$ (ou $x=-2$) est un nombre réel vérifiant l'égalité.
Il y a bien existence d'une solution (au sens d'au moins une solution) même s'il n'y a pas unicité de celle-ci (puisqu'il y a deux solutions possibles).

Pour prouver qu'une propriété du type "Il existe un ..." qui vérifie une certaine propriété, il suffit de trouver un exemple pour lequel la propriété est vérifiée.

Pour prouver qu'une propriété du type "Pour tout ..." ou "Quel que soit ...", il ne suffit pas de la vérifier sur quelques exemples, mais il faut la démontrer en tout généralité en utilisant des lettres comme $x$ ou $n$.

Pour la suite, vous aurez besoin de connaître les définitions suivantes :

  1. Démontrer qu'il existe un carré d'un nombre entier qui est impair.

  2. Démontrer que la différence des carrés de deux entiers consécutifs est impaire.

Code de déblocage de la correction :

Soient $P$ et $Q$ deux propositions mathématiques.

  1. La proposition "$P$ et $Q$" est :

    • vraie lorsque $P$ et $Q$ sont toutes les deux vraies.

    • fausse lorsqu'au moins l'une des deux est fausses.

    On peut visualiser cela grâce à cette table de vérité de $P$ et $Q$ :

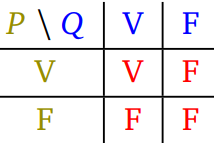
  2. La proposition "$P$ ou $Q$" est :

    • fausse lorsque $P$ et $Q$ sont toutes les deux fausses.

    • vraie lorsqu'au moins l'une des deux est vraies.

    On peut visualiser cela grâce à cette table de vérité de $P$ ou $Q$ :

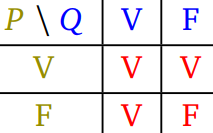
La négation d'une proposition mathématique $P$ est la proposition, notée non $P$, qui est vraie lorsque $P$ est fausse et fausse lorsque $P$ est vraie.

On peut visualiser cela grâce à cette table de vérité de non $P$ :

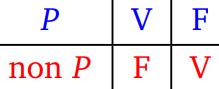
Parmi les énoncés suivants, cocher ceux qui correspondent à une équivalence (vraie), sachant que $P$, $Q$ et $R$ sont trois propositions mathématiques :

$P \iff non(non(P))$
$non(P\ et\ Q) \iff non\ P\ et\ non\ Q$
$non(P\ et\ Q) \iff non\ P\ ou\ non\ Q$
$non(P\ ou\ Q) \iff non\ P\ et\ non\ Q$
$non(P\ ou\ Q) \iff non\ P\ ou\ non\ Q$
$P\ et\ (Q\ ou\ R) \iff (P\ et\ Q)\ ou\ (P\ et\ R)$
$P\ et\ (Q\ ou\ R) \iff (P\ ou\ Q)\ et\ (P\ ou\ R)$
$P\ ou\ (Q\ et\ R) \iff (P\ et\ Q)\ ou\ (P\ et\ R)$
$P\ ou\ (Q\ et\ R) \iff (P\ ou\ Q)\ et\ (P\ ou\ R)$

Une fois les équivalences (vraies) reconnues cochées, vérifier vos réponses en cliquant sur ce bouton :

On retrouve ce qui a été vu en probabilités :

Si $A$ et $B$ sont deux événements, on note "$A$ et $B$" $A\cap B$, "$A$ ou $B$" $A\cup B$ et "non A" $\overline{A}$.
De plus, on a :

Notons $P(x)$ une proposition mathématique dépendant de $x$.

Écrire la négation des propositions mathématiques suivantes :

  1. "Il existe un réel $x$ tel que pour tout entier naturel $n$ on a : $x+n\ge 10$", qui s'écrit mathématiquement ainsi : $\exists x\in\mathbb{R}\ \forall n\in\mathbb{N}\ x+n\ge 10$.

  2. "Tout élève qui suit la formation au concours général réussira mieux ce concours ou verra ses compétences mathématiques augmenter".

Code de déblocage de la correction :

Implication, réciproque et contraposée

Si vous maîtrisez ces notions d'implication, de réciproque et de contraposée, passez directement au premier exercice en lien, sinon, vous pouvez lire les définitions et exemples ci-dessous ainsi que la méthode (pour surtout retenir les trois étapes à suivre lors d'une démonstration par contraposée).
Vous pouvez aussi regarder la vidéo issue du cours de maths expertes de ce site.

Le connecteur implication est un connecteur binaire entre deux propositions $A$ et $B$ :

Si $ A $ est vraie alors $B$ est vraie

On peut noter aussi :

$ A \Longrightarrow B$.

Théorème de Pythagore :
Si $ABC$ est un triangle rectangle en $A$ alors $AB^2 + AC^2 = BC^2$.

La réciproque d'une implication "$A$ implique $B$" est la proposition :

"$B$ implique $A$"

On peut noter aussi:

$B\Longrightarrow A$

Réciproque du théorème de Pythagore :
Si $AB^2 + AC^2 = BC^2$ alors $ABC$ est un triangle rectangle en $A$.

La contraposée d'une implication "$A$ implique $B$" est la proposition :

Si $B$ n'est pas vraie alors $A$ n'est pas vraie

On peut noter aussi:

$(Non B)\Longrightarrow(Non A)$

Contraposée du théorème de Pythagore :
Si $AB^2 + AC^2 \ne BC^2$ alors $ABC$ n'est pas un triangle rectangle en $A$.

Une implication est équivalente à sa contraposée.

Autrement dit, pour démontrer une implication, nous pouvons montrer sa contraposée et réciproquement.

  1. La proposition "s'il pleut, alors le sol est mouillé" est vraie.
    Sa contraposée, "si le sol n'est pas mouillé, alors il ne pleut pas" est elle aussi vraie.

  2. Par contre la proposition réciproque "si le sol est mouillé, alors il pleut" est fausse (il peut avoir plu, la pluie a cessé mais le sol reste encore humide).
    Sa contraposée, "s'il ne pleut pas, alors le sol n'est pas mouillé" est elle aussi fausse (pour la même raison).

L'exemple précédent prouve bien qu'il ne faut pas confondre " proposition contraposée" et "proposition réciproque".

Voici un exemple d'utilisation de la contraposée pour démontrer la proposition suivante : "Soit $x$ un nombre réel. Si $x^3=7$, alors $x\lt 2$.".

Étape 1 : écrire la contraposée de la proposition
La contraposée de la proposition "Si $x^3=7$, alors $x\lt 2$" est "si $x\ge 2$, alors $x^3\neq 7$".

Étape 2 : prouver que la contraposée est vraie
Si $x\ge 2$, alors si $x^3\ge 2^3$ puisque la fonction cube est croissante sur l'intervalle $[2;+\infty[$.
Comme $x^3\ge 8$, forcément $x^3\neq 7$".
On a ainsi prouver que "si $x\ge 2$, alors $x^3\neq 7$".

Étape 3 : conclure
Comme l'affirmation "si $x\ge 2$, alors $x^3\neq 7$" est vraie, sa contraposée "Si $x^3=7$, alors $x\lt 2$." est elle aussi vraie.

Vidéo :

Soit $n$ un nombre entier supérieur ou égal à 2.

Démontrer que si $2^n-1$ est un nombre premier alors $n$ est un nombre premier.

Rappel de la définition :
Un nombre premier est un nombre entier naturel possédant exactement deux diviseurs entiers naturels : 1 et lui-même.

Code de déblocage de la correction :

Raisonnement par l'absurde

Si vous maîtrisez le raisonnement par l'absurde, passez directement au premier exercice en lien, sinon, vous pouvez lire la définition ainsi que la méthode (pour surtout retenir les trois étapes à suivre lors d'une démonstration par l'absurde).
Vous pouvez aussi regarder la vidéo issue du cours de maths expertes de ce site.

Le raisonnement par l'absurde est un raisonnement qui permet de démontrer qu'une affirmation est vraie en montrant que son contraire est faux. Il s'appuie sur la règle logique que :

Si "non P" est faux, alors P est vraie.

Concrètement, pour démontrer une propriété $P$, on supposera que $P$ est fausse et on essaiera d'obtenir une absurdité.

Voici un exemple de mise en oeuvre de ce raisonnement en essayant de prouver l'affirmation suivante :
"0 n'a pas d'inverse".

Étape 1 : supposer comme vraie le contraire de l'affirmation
On suppose ici que 0 admet un nombre réel inverse, noté ici $a$.
Cela signifie par définition de l'inverse que $a\times 0 = 1$.

Étape 2 : déduire des conséquences pour aboutir à une contradiction
$1=a\times 0$.
Comme $0=0+0$, on en déduit que $1 = a\times (0+0)$, soit en développant $1=a\times 0 +a \times 0$.
Or, $a\times 0 = 1$, donc, en remplaçant dans le second membre, on en déduit que $1=1+1$.
On aboutit à $1=2$. Ceci est évidemment impossible, une contradiction avec ce que vous savez comme vrai.

Étape 3 : conclure en citant le raisonnement utilisé
Comme l'hypothèse de départ "0 admet un nombre réel inverse" aboutit à une contradiction, cette hypothèse est fausse.
Dès lors, son contraire est vrai, c'est-à-dire "0 n'admet pas d'inverse".
On a prouvé en utilisant le raisonnement par l'absurde que "0 n'a pas d'inverse".

Vidéo :

Contrairement aux exercices du baccalauréat où vous êtes guidé.e.s et où chaque question correspond souvent à une seule idée, au concours général, il peut être utile de remarquer quelques observations afin de prouver un résultat général.
Cet exercice en est un exemple : avant d'obtenir une égalité de valeurs sur $a$ et $b$, on commence par observer que nécessairement il y a une égalité de signes entre $a$ et $b$, cette remarque étant utile pour démontrer ensuite le résultat dans toute sa profondeur.

Soient $a$ et $b$ deux réels.
Démontrer que si $\dfrac{a}{1+b^2}=\dfrac{b}{1+a^2}$ alors $a=b$.

Montrer d'abord que $a$ et $b$ sont de même signe.

Code de déblocage de la correction :

Soit $m$ est un nombre entier impair

Démontrer que $\sqrt{2m}$ est un nombre irrationnel.

Vous pouvez admettre ici que tout nombre rationnel peut être écrit sous la forme d'une fraction irréductible $\dfrac{a}{b}$ où $a$ et $b$ deux nombres entiers tels qu'aucun nombre ne divise à la fois $a$ et $b$.

Code de déblocage de la correction :

Raisonnement par contre-exemple

Pour montrer qu'une proposition mathématique est fausse (c'est-à-dire pour l'infirmer), il suffit d'en donner un contre-exemple.

La proposition "Pour tout réel strictement positif $x$, $x\ge \dfrac{1}{x}$" est fausse car elle est fausse par le cas particulier au $x=\dfrac{1}{2}$.
En effet, dans ce cas, $x=\dfrac{1}{2}$ et $\dfrac{1}{x}=2$.

Que pensez-vous de l'affirmation : "tout nombre entier naturel peut être écrit comme la somme de trois carrés de nombres entiers." ?

Code de déblocage de la correction :

Raisonnement par disjonction des cas

Si vous maîtrisez le raisonnement par disjonction de cas, passez directement au premier exercice en lien, sinon, vous pouvez lire la définition ainsi que la méthode (pour surtout retenir les trois étapes à suivre lors d'une démonstration par disjonction de cas).
Vous pouvez aussi regarder la vidéo issue du cours de maths expertes de ce site.

Lors d'un raisonnement par disjonction des cas, on étudie tous les cas possibles en faisant au préalable un tri pour restreindre le nombre de cas à étudier.

Voici un exemple d'utilisation de la disjonction de cas pour démontrer la proposition suivante :
"Pour tout réel $x$ de l'intervalle $]-2;1]$, $0\le |x| \lt 2$".

Étape 1 : séparer en plusieurs cas disjoints dont la réunion correspond à l'ensemble des cas possibles
L'intervalle $]-2;1]$ est découpé en deux intervalles : $]-2;0]$ et $]0;1]$. Il y a donc deux cas à étudier.

Étape 2 : étudier chaque cas séparément

  1. Cas où $x\in ]-2;0]$ :
    Si $x\in ]-2;0]$ alors $-2 \lt x \le 0$. En multipliant par $-1$ négatif, on a : $2 \gt -x \ge 0$.
    Comme $x\le 0$, $|x|=-x$, on déduit donc de $2 \gt -x \ge 0$ que $0\le |x| \lt 2$.
    On a donc prouvé dans ce cas que $0\le |x| \lt 2$.

    On aurait aussi pu utiliser ici les variations de la fonction valeur absolue sur $]-2;0]$.

  2. Cas où $x\in ]0;1]$ :
    Si $x\in ]0;1]$ alors $0 \lt x \le 1$.
    Comme $x\ge 0$, $|x|=x$, on déduit donc de $0 \lt x \le 1$ que $0\lt |x| \le 1$.
    A fortiori, on a donc : $0\le |x| \lt 2$ car $]0;1]\subset [0;2[$
    On a donc prouvé dans ce cas que $0\le |x| \lt 2$.

Étape 3 : conclure
Comme dans chacun des cas possibles pour $x$, on a bien $0\le |x| \lt 2$, on a prouvé par disjonctions de cas que : "Pour tout réel $x$ de l'intervalle $]-2;1]$, $0\le |x| \lt 2$".

Vidéo :

Exercice ici du Concours Général de 2017

Prouver que si $x$ est un entier alors il existe un entier $t$ tel que $x^2$ soit égal à $8t$ ou à $8t+1$ ou à $8t+4$.

Code de déblocage de la correction :

Équivalence et double implication

Si vous n'avez pas déjà rencontré le raisonnement par double implication afin de prouver une équivalence, vous pouvez :

Raisonner par double implication.

$P$ équivaut à $Q$ si, et seulement si $P\Longrightarrow Q$ et $Q \Longrightarrow P$.

On note $P \Longleftrightarrow Q$

Concrètement, ce type de raisonnement se fera en deux étapes :

  1. $P\Longrightarrow Q$
  2. $Q\Longrightarrow P$

Voici un exemple de mise en oeuvre de ce raisonnement en essayant de prouver la proposition suivante :
"Soit $x>0$. $x^2>x \iff x>1$".

Étape 1 : Prouver une des implications
On suppose ici que $x>1$. Le but de montrer que $x^2>x$.
Comme $x>1$, $x$ est positif, donc en multipliant chaque membre de l'inégalité par $x$, on en déduit que : $x\times x>1\times x$.
Ainsi, on a prouvé le "sens réciproque" : "si $x>1$ alors $x^2>x$".

Étape 2 : Prouver l'implication réciproque
On suppose ici que $x^2>x$, avec $x>0$. Le but de montrer que $x>1$.
Montrons ici que la contraposée de cette implication est vraie, c'est-à-dire que "si $0\le x \le 1$ alors $x^2\le x$".
Comme $0\le x \le 1$, $x$ est positif, donc en multipliant chaque membre de l'inégalité par $x$, on en déduit que : $0\le x\times x \le 1\times x$.
Ainsi, on a prouvé que "si $0\le x \le 1$ alors $x^2\le x$".
La contraposée est donc elle aussi vraie soit pour $x\gt 0$ "si $x^2>x$ alors $x>1$." Ainsi, on a prouvé le "sens direct" : "si $x^2>x$ alors $x>1$".

Étape 3 : conclure
Comme on a prouvé que, pour $x\lt 0$, "si $x>1$ alors $x^2>x$" et sa réciproque "si $x^2>x$ alors $x>1$", on a montré par double implication que, pour $x\lt 0$, "$x>1 \iff x^2>x$".

Début de l'arithmétique

Divisibilité dans $\mathbb{Z}$

Soient $a$ et $b$ deux entiers relatifs, avec $a$ non nuls

Dire que $b$ divise $a$ signifie qu'il existe un entier relatif $k$ tel que $a=bk$.

On note $b|a$.

On dit aussi que $b$ est un diviseur de $a$ ou que $a$ est un multiple de $b$.

Les seuls diviseurs de $1$ et $-1$ sont $1$ et $-1$.

  1. Transitivité : Si $c|b$ et $b|a$ alors $c|a$.

  2. Si $a|b$ et $b|a$ alors $|a|=|b|$.

  3. Si $c$ divise $a$ et $b$ alors, pour tout entier $u$ et $v$, $c$ divise $au+bv$.

Cliquer pour afficher la démonstration

  1. Soient $a\in \mathbb{Z}$, $b\in \mathbb{Z}$ et $c\in \mathbb{Z}$.
    Supposons que $c|b$. Il existe $k\in \mathbb{Z}$ tel que $b= k\times c$.
    De même, supposons que $b|a$. Il existe $p\in \mathbb{Z}$ tel que $a= p\times b$.
    Dès lors, $a= p\times b = p\times k\times c = (pk)\times c = (pk)\times c = k'\times c$ avec $k'=p\times k$.
    Comme $k\in \mathbb{Z}$ et $p\in \mathbb{Z}$, $k'\in \mathbb{Z}$, ainsi $c|a$.

  2. Si $a|b$ et $b|a$ alors il existe $k\in \mathbb{Z}$ et $p\in \mathbb{Z}$ tels que $b= k\times a$ et $a= p\times b$.
    Dès lors, $a= p\times b = p\times k\times a$, d\'où $a - kp\times a = 0$ soit $a\times(1-kp) = 0$.
    Comme $a$ est un diviseur, par définition, $a$ est non nul donc $1-kp = 0$, soit $kp=1$.
    Or, $k\in \mathbb{Z}$ et $p\in \mathbb{Z}$ donc $p$ est un diviseur de $1$, comme les seuls diviseurs de 1 sont 1 ou -1, donc $p = 1$ ou $p=-1$.

    • si $p = 1$ alors $a = p\times b = b$.

    • si $p = -1$ alors $a = p\times b = -b$.

    On sait que $|a|=|b|$ signifie que $a = b \text{ ou } a = -b$.
    Par conséquent, si $a|b$ et $b|a$ alors $a = b \text{ ou } a = -b$ soit $|a|=|b|$.

  3. Soient $u\in \mathbb{Z}$ et $v\in \mathbb{Z}$.
    Si $c$ divise $a$ et $b$ alors, il existe $k\in \mathbb{Z}$ et $p\in \mathbb{Z}$ tels que $a= k\times c$ et $b= p\times c$ donc $au + bv = k\times c \times u + p\times c \times v = c\times(ku + pv)= k'\times c$ avec $k' = ku + pv$.
    Puisque $k$, $p$, $u$ et $v$ sont des entiers relatifs, $k' = ku + pv\in \mathbb{Z}$.
    Par conséquent, $c$ divise $au+bv$.
    Ainsi, si $c$ divise $a$ et $b$ alors, pour tout entier $u$ et $v$, $c$ divise $au+bv$.

Voici des critères de divisibilité, peut-être déjà connus, et qui peuvent être facilement démontrés une fois la notion de congruence vue :

Déterminer tous les entiers relatifs $n$ tels que $(5n+4)|(3n+1)$.

Utiliser une combinaison linéaire de $5n+4$ et de $3n+1$ afin d'éliminer l'inconnue $n$.

Code de déblocage de la correction :

Nombres premiers

On appelle nombre premier tout nombre entier naturel possédant exactement 2 diviseurs dans $\mathbb{N}$ : 1 et lui-même.

On peut obtenir la liste des premiers nombres premiers avec le crible d'Ératosthène : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, ...

Tout entier naturel supérieur ou égal à 2 est divisible par un nombre premier.

Cliquer pour afficher la démonstration

Soit $n$ un entier naturel supérieur ou égal à 2.
Notons $P(n)$ la proposition mathématique : "tout entier naturel compris entre 2 et $n$ admet un diviseur premier".
Montrons par récurrence que cette propriété est vrai pour tout entier naturel $n$ supérieur ou égal à 2.

Initialisation : avec $n=2$

2 est un nombre premier et 2 divise 2 donc $P(2)$ est vraie.

Hérédité :
Considérons un entier naturel $k\ge 2$ tel que $P(k)$ soit vraie.
Montrons que $P(k+1)$ est vraie.

Par hypothèse de récurrence avec $P(k)$, tous les nombres entiers naturels compris entre 2 et $k$ sont divisibles par un nombre premier.
Il reste à démontre que $k+1$ est lui aussi divisible par un nombre premier. Deux cas se présentent :

On a montré que $k+1$ admet toujours un diviseur premier donc $P(k+1)$ est vraie.

La propriété étant vraie pour $n=2$ et étant héréditaire, on a prouvé par récurrence que, pour tout entier naturel $n\ge 2$ possède un diviseur premier.

Soit $n$ un entier supérieur ou égal à 2.
$n$ est premier si, et seulement si, $n$ n'a pas de diviseur premier inférieur ou égal à $\sqrt{n}$ autre que 1.

La démonstration de cette propriété utilise une idée à retenir que l'on retrouvera plus tard : le fait que tout ensemble non vide de nombres entiers naturels possède un plus petit élément.

Cliquer pour afficher la démonstration

Sens direct
On suppose que $n$ est premier.
Comme $n$ ne possède que deux diviseurs : 1 et $n$, 1 est le seul diviseur de $n$ inférieur ou égal à $\sqrt{n}$.
Ainsi, $n$ n'a pas de diviseur premier inférieur ou égal à $\sqrt{n}$.

Sens réciproque
On considère un entier naturel $n$ n'ayant pas de diviseur premier inférieur ou égal à $\sqrt{n}$.
Montrons, en raisonnant par l'absurde, que $n$ est premier.
Supposons que $n$ n'est pas premier.

Comme $n \ge 2$ n'est pas premier, il admet au moins un autre diviseur que 1 et $n$.
L'ensemble des diviseurs de $n$ ( dans $\mathbb{N}$ ) autres que 1 et $n$ est donc non vide, il admet un plus petit élément $p$.

On peut montrer, encore par raisonnement par l'absurde que $p$ est premier.
En effet, si $p$ n'était pas premier il serait divisible par un nombre $m$ différent de 1 et de $p$. Ce nombre $m$ serait par transitivité aussi un diviseur de $n$ mais plus petit que le plus petit existant : $p$.

Comme $p$ divise $n$, il existe un entier $k$ tel que $n=pk$.
Forcément $k\leq n$ en tant que diviseur.
Comme $p$ est le plus petit des diviseurs de $n$, le diviseur $k$ est plus grand que $p$.
Ainsi: $1< p\leq k<n$

Or, on a:
Première inégalité : $p\leq p$.
Deuxième inégalité : $p\leq k$.
Par produit des deux inégalités, l'ordre en conservé (puisque tous les nombres sont positifs), on a donc : $p\times p \leq p\times k$, c'est-à-dire $p^2\leq n$.

Comme $p^2\leq n$, $p\leq\sqrt{n}$. Ainsi $p$ est un diviseur de $n$ qui est un nombre premier et qui est compris entre 1 et $\sqrt{n}$.
Ceci est contradictoire avec le fait que $n$ n'a pas de diviseur premier inférieur ou égal à $\sqrt{n}$.
Ainsi, l'hypothèse initiale selon laquelle $n$ n'est pas premier est fausse.
Ainsi, $n$ est un nombre premier.

On a finalement montré que $n$ est un nombre premier si, et seulement si, $n$ n'admet pas de diviseur premier compris entre 1 et $\sqrt{n}$.

Pour démontrer qu'un nombre $n$ est premier, il suffit de :

Il existe une infinité de nombres premiers.

Cliquer pour afficher la démonstration

Démontrons ce résultat par un raisonnement par l'absurde.
Supposons donc qu'il existe un nombre fini $n$ de nombres premiers.
On peut donc les numéroter $p_1$, $p_2$, $p_3$, ..., $p_n$.
Considérons le nombre $m=p_1\times p_2\times p_3\times...\times p_n+1$.
Comme 1 est divisible par aucun des $n$ nombres premiers $p_i$, le nombre $m$ est divisible par aucun de ces $n$ nombres premiers, c'est-à-dire par aucun nombre premier.
Or, tout nombre supérieur ou égal à 2 admet un diviseur premier. Il y a une contradiction.
L'hypothèse initiale selon laquelle il existe un nombre fini de nombres premiers est fausse.
On a démontré qu'il existe une infinité de nombres premiers.

Théorème fondamental de l'arithmétique
Tout nombre entier $n$ supérieur ou égal à 2 se décompose de manière unique (à l'ordre près des facteurs) en produit de nombres premiers.
Plus précisément, pour tout nombre entier $n\ge 2$ il existe $k\ge 1$ nombres premiers $p_1$, $p_2$, ..., $p_k$ et $k\ge 1$ entiers naturels non nuls $\alpha_1$, $\alpha_2$, ... et $\alpha_k$ tel que $n=p_1^{\alpha_1}\times p_2^{\alpha_2}\times...\times p_k^{\alpha_k}$.

Cliquer pour afficher la démonstration

Ce théorème signifie qu'il y a l'existence d'une telle décomposition puis son unicité.
La démonstration doit donc se faire en deux temps.

Prouvons d'abord l'existence d'une telle décomposition :
Soit $P(n)$ la proposition "Tout entier $m$ compris entre 2 et $n$ se décompose en produit de nombres premiers".
Montrons par récurrence que cette propriété est vraie pour tout entier naturel $n\ge 2$.

Initialisation : avec $n=2$
$2=2^1$ et $2$ est un nombre premier, ainsi $P(2)$ est vraie.

Hérédité :
Considérons un entier naturel $k\ge 2$ tel que $P(k)$ soit vraie.
Montrons que $P(k+1)$ est vraie.

Deux cas se présentent :

Comme dans tous les cas, $k+1$ peut s'écrire comme produit de nombres premiers, $P(k+1)$ est vraie.

On a démontré par récurrence que Tout nombre premier $n$ supérieur ou égal à 2 se décompose en produit de nombres premiers.

Démontrons l'unicité de la décomposition :
Supposons que $n$ possède deux écritures sous forme de produit de nombres premiers.
Notons $p$ un nombre premier apparaissant dans la première écriture de décomposition et $\alpha$ son exposant dans cette décomposition de $n$.
Notons $\beta$ l'exposant apparaissant pour $p$ dans la seconde décomposition ; $\beta=0$ si $p$ n'y apparaît pas.
On peut donc écrire à la fois $n=p^{\alpha}\times a$, où $a$ est le produit des nombres premiers distincts de $p$ et $n=p^{\beta}\times b$, où $b$ est le produit des nombres premiers distincts de $p$.
En comparant $\alpha$ et $\beta$, il y a trois cas possibles :

On a prouvé que dans chaque décomposition possible apparaissent les mêmes facteurs premiers avec le même exposant.
Il y a donc unicité de la décomposition à l'ordre près des facteurs.

Décomposer le nombre 750 en produit de facteurs premiers.

Code de déblocage de la correction :

Division euclidienne

Division euclidienne dans $\mathbb{N}$.

Soit $a \in \mathbb{N}$ et $b \in \mathbb{N}^*$, alors il existe un unique couple d'entiers naturels $(q;r)$ tel que $a=bq+r$ avec $0 \leq r < b$.
Cela correspond à une écriture en ligne de la division posée vue dès le primaire : .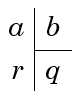

Vocabulaire

$a$ est le dividende, $b$ est le diviseur, $q$ est le quotient et $r$ est le reste.

Cliquer pour afficher la démonstration

Existence du couple $(q;r)$

Soit $q$ la partie entière du quotient $\dfrac{a}{b}$. L'entier $q$ est défini par l'encadrement $q\leq \dfrac{a}{b} < q+1$ ; $q$ est la partie entière de $\dfrac{a}{b}$.

Puisque $b> 0$, on en déduit par produit que $bq \leq a < b(q+1)$ (*)

On pose alors $r=a-bq$. Ainsi $a=bq+r$ et d'après l'encadrement (*), $bq-bq \leq a-bq < bq+q-bq$

soit $0\leq r < q$.

Unicité du couple $(q;r)$

On suppose qu'il existe deux couples d'entiers naturels $(q;r)$ et $(q';r')$ vérifiant simultanément :

$a=bq+r = bq'+r'$ avec $0 \leq r<b$ et $0 \leq r' \lt b$.

On en déduit que $r-r' = a-bq-(a-bq') = b(q-q')$ donc $r-r'$ est multiple de $b$.

Or, $0 \leq r < b$ et $-b < -r' \leq 0$ donc, par addition membre à membre, on obtient $-b \lt r-r'\lt b$

Le seul multiple de $b$ dans $]-b;b~[$ est $0$ donc $r-r'=0$ soit $r=r'$.

Comme $r-r'=b(q'-q)$ avec $b \neq 0$, alors $q'-q = 0$ soit $q=q'$, d'où l'unicité.

Division euclidienne dans $\mathbb{Z}$.

Soit $a \in \mathbb{Z}$ et $b \in \mathbb{Z}^*$, alors il existe un unique couple d'entiers $(q;r)$ avec $q \in \mathbb{Z}$ et $r \in \mathbb{N}$ tel que $a=bq+r$ avec $0 \leq r < |b|$.

Conséquences :

Tout entier relatif $n$ peut être écrit sous la forme :

Nombres de Fermat

On appelle nombre de Fermat les nombres entiers pouvant s'écrire sous la forme $F_n=2^{2^n}+1$, avec $n\in\mathbb{N}$.

  1. Démontrer que si $2^k+1$ est un nombre premier alors $k$ est nécessairement une puissance de 2.

    Code de déblocage de la correction :

  2. Démontrer que, pour tout entier naturel $n$ non nul, $F_{n}-2$ est divisible par $F_{n-1}$.

    Code de déblocage de la correction :

  3. En déduire que pour tout entier naturel $n$, $F_n$ et $F_{n+1}$ sont premiers entre eux, c'est-à-dire ont pour seuls diviseurs commun 1 et -1.

    4. Code de déblocage de la correction :

On désigne par $d(n)$ le nombre de diviseurs strictement positifs de l’entier $n$.
Montrer que $d(n)$ est impair si, et seulement si, $n$ est un carré.

Code de déblocage de la correction :

On définit la suite $(a_n)_{n\ge 1}$ de la manière suivante $a_1 = 2025^{2025}$ et pour $n\ge 0$, $a_{n+1}$ est la somme des chiffres de $a_n$.
Calculer $a_5$ puis montrer que la suite $(a_n)_{n\ge 1}$ est constante à partir d'un certain rang.

Code de déblocage de la correction :

Théorèmes d'existence

Pour prouver l'existence d'un objet mathématique, la méthode naïve est de construire cet objet.
Parfois, il va être possible de prouver qu'un objet existe sans directement le construire en utilisant des théorèmes d'existence.

Les théorèmes qui prouve l'existence d'objets mathématiques sont des théorèmes très profonds.
Vous avez déjà rencontré le théorème des valeurs intermédiaires ou les théorèmes de convergence de suite qui permette de justifier l'existence d'un réel particulier sans pour autant le connaître de manière exacte.
D'autres théorèmes existent, découvrons-les !

$\mathbb{N}$ : ensemble bien ordonné

Toute partie non vide de $\mathbb{N}$ possède un plus petit élément.

Soient $a$ et $b$ deux nombres entiers naturels non nuls.
Démontrer qu'il existe un plus petit nombre multiple à la fois de $a$ et de $b$. Ce nombre est appelé le PPCM de $a$ et de $b$ (Plus Petit Commun Multiple).

Code de déblocage de la correction :

Considérons deux nombres entiers non nuls $a$ et $b$ premiers entre eux, c'est-à-dire n'ayant comme diviseur commun que 1 et -1.
On considère l'ensemble $D$ des combinaisons linéaires strictement positives de $a$ et $b$ : $D=\{au+bv>0|u\in\mathbb{Z},v\in\mathbb{Z}\}$.

  1. Démontrer que l'ensemble $D$ admet un plus petit élément $d$.

  2. Prouver que $d=1$.

Code de déblocage de la correction :

Principe des tiroirs

Principe des tiroirs (de Dirichlet)
Si $n$ chaussettes occupent $m$ tiroirs et si $n\gt m$, alors au moins un des tiroirs contient au moins deux chaussettes.

Exercice ici du Concours Général de 2022

Soit $k$ et $l$ deux entiers naturels non nuls. On veut répartir $kl$ chemises parmi $k$ tiroirs.
Démontrer qu'au moins un de ces $k$ tiroirs contiendra au moins $l$ chemises.

Code de déblocage de la correction :

Pour vous entraîner au Concours Général, vous avez décidé de faire 130 séances de travail en mathématiques sur les 100 prochains jours.

  1. Justifier qu'il existe au moins un jour où vous effectuerez au moins deux séances de travail en mathématiques.

  2. Démontrer qu'il y aura une suite de jours consécutifs au cours desquels vous ferez exactement 41 séances de travail.

Code de déblocage de la correction :

Principe de descente infinie de Fermat

Si une proposition $P(n)$ dépendant d'un entier naturel $n$ vérifie la propriété suivante "Si $P$ est vraie à un rang quelconque $q$ implique qu'elle est vraie à un rang strictement inférieur $r$", alors la proposition $P(n)$ est fausse pour toute valeur de $n$.

Cliquer pour afficher la démonstration

En effet, le principe de récurrence appliquée à la propriété conduirait à l'existence d'une suite infinie de rangs strictement décroissants : $q>r>...$. Or comme ces rangs sont des nombres entiers naturels, cette "infinie" ne peut avoir plus de $q+1$ valeurs : toute suite d'entiers naturels strictement décroissante est forcément finie.

Voici une démonstration plus rigoureuse :

Supposons, par un raisonnement par l'absurde, que la proposition $P(n)$ est vraie pour au moins un entier naturel.
L'ensemble des entiers naturels pour lesquels la proposition $P(n)$ est vraie est dès lors une partie non vide de $\mathbb{N}$ ; cet ensemble admet donc un plus petit élément $m$.
D'après la propriété "$P$ est vraie à un rang $m$ implique que $P$ est vraie à un rang strictement inférieur $r$", il existe donc un entier $r$, strictement inférieur à $m$, tel que la proposition $P(r)$ soit vraie.
Cet entier $r$ contredit le fait que $m$ est le plus petit entier naturel $n$ tel que $P(n)$ soit vraie.
On en déduit que l'hypothèse de départ "la proposition $P(n)$ est vraie pour au moins un entier naturel." est fausse ; dès lors, la proposition $P(n)$ est fausse pour tout entier naturel $n$.

Voici une autre manière voir, beaucoup moins rigoureuse, pour comprendre ce résultat :

Notons $m$ le plus petit entier tel que la proposition $P(n)$ soit vraie.

  • $m$ ne peut pas être égal à 0 car si $P$ est vraie au rang $0$ alors elle est vraie à un rang strictement inférieur à 0 en appliquant la propriété d'hérédité inverse : "Si $P$ est vraie à un rang quelconque $q$ implique qu'elle est vraie à un rang strictement inférieur $r$".
    Or, il n'existe pas de rang strictement négatif. Ainsi, $m\neq 0$.

  • De même, $m$ ne peut pas être égal à 1 car si $P$ est vraie au rang $1$ alors elle est vraie à un rang strictement inférieur à 1.
    Or, le seul tel rang possible est 0, qui ne convient pas. Ainsi, $m\neq 1$.

  • De même, $m$ ne peut pas être égal à 2 car si $P$ est vraie au rang $1$ alors elle est vraie à un rang strictement inférieur à 2.
    Or, les seuls tels rangs possibles (0 et 1) ne conviennent pas. Ainsi, $m\neq 2$.

  • On peut ainsi remonter (par récurrence) pour démontrer qu'aucune valeur entière naturelle ne convient pour $m$ : ainsi un tel entier $m$ n'existe pas.

Ce principe est connu dès l'Antiquité car il apparaît dans les Éléments d'Euclide écrits possiblement vers 300 avant notre ère. Il a été très utilisé au $\text{XVII}^e$ siècle par Pierre de Fermat si bien que l'on attache désormais son nom à cette méthode.
Il est souvent utile pour démontrer qu'il n'existe pas de solution à une équation (diophantienne) donnée, comme le faisait Fermat.

Considérons l'équation $x^3+3y^3=9z^3$ $(E)$, où $x$, $y$ et $z$ sont des nombres entiers.
Le but est de résoudre cette équation

  1. Trouver un triplet $(x;y;z)$ qui est solution évidente à cette équation.

  2. On suppose l'existence d'un triplet non nul $(x;y;z)$ qui est solution de cette équation $(E)$.

    1. Justifier que $x$ est forcément un multiple de 3.

      2. Code de déblocage de la correction :

    2. Justifier que le triplet $\displaystyle \left( \dfrac{x}{3};\dfrac{y}{3};\dfrac{z}{3} \right)$ est un triplet de nombres entiers encore solution de l'équation $(E)$.

    3. Conclure quant à l'existence d'un triplet non nul $(x;y;z)$ qui est solution de cette équation $(E)$.

  3. Conclure quant aux solutions entières de l'équation $x^3+3y^3=9z^3$ $(E)$.

Code de déblocage de la correction :

Exercices

Trouver tous les entiers strictement positifs $x$, $y$ et $z$ tels que $\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1$.

Comme les inconnues jouent un rôle symétrique, on peut supposer sans perdre en généralité que $0 \lt x \le y \le z$.

Code de déblocage de la correction :

Exercice ici du Concours Général de 2017

Prouver que si $a$, $b$, $c$ et $d$ sont des entiers tels que $7a^2=b^2+c^2+d^2$, alors $a=b=c=d=0$.

On pourra utiliser le fait déjà démontré que si $x$ est un entier alors il existe un entier $t$ tel que $x^2$ soit égal à $8t$ (cas où $x$ est multiple de 4) ou à $8t+1$ (cas où $x$ est impair) ou à $8t+4$ (cas où $x$ s'écrit sous la forme $x=2k$ avec $k$ impair) pour démontrer qu'il est impossible qu'au moins un des quatre nombres $a$, $b$, $c$ ou $d$ soit impair.

Code de déblocage de la correction :

Exercice(s) à chercher pour la prochaine fois

Extrait du Concours général 2012

Pour tout entier $n \ge 2$, on dispose de la décomposition en facteurs premiers $n = p_1^{a_1}p_2^{a_2}...p_k^{a_k}$, où $p_1$, $p_2$, ..., $p_k$, qu'on suppose distincts, sont les diviseurs premiers de $n$, et où les exposants $a_1$, $a_2$, ..., $a_k$ sont des entiers strictement positifs.
On pose alors $f(n) = a_1^{p_1}\times a_2^{p_2}\times...\times a_k^{p_k}$.
Par exemple, si $n = 720 = 2^4\times 3^2\times 5^1$, on a $f(n) = 4^2\times 2^3\times 1^5 = 128$. En posant de plus $f(1) = 1$, on obtient une fonction $f$ de $\mathbb{N}^*$ dans $\mathbb{N}^*$.
Enfin, pour tout entier $n \ge 1$ et $i \ge 0$, on note $f^0(n) = n$ et $f^{i+1}(n) = f( f^i(n))$.
Par exemple : $f^0(720) = 720$ ; $f^1(720) = f(720) = 128$ ; $f^2(720) = f(128) = 49$.
Le but de ce problème est d'étudier le comportement de la fonction $f$ et des suites $(f^i(n))_{i\in\mathbb{N}}$ pour $n$ fixé.

    1. Calculer $f(2012)$ et $f(2023)$.

    2. Déterminer les nombres $f^i(36^{36})$ pour $0 \le i \le 3$.
      Que peut-on dire des suivants ?

    1. Donner un exemple d'entier $n \ge 1$ tel que, pour tout entier naturel $i$, on ait $f^{i+2}(n) = f^i(n)$ et $f^{i+1}(n) \neq f^i(n)$.

    2. Montrer que la fonction $f$ n'est ni croissante ni décroissante.

    3. Résoudre :

    1. l'équation $f(n)=1$.

    2. l'équation $f(n)=2$.

    3. l'équation $f(n)=4$.

Code de déblocage de la correction :

Un exercice facultatif qui peut être démontré de plusieurs manières en utilisant différents raisonnements vus aujourd'hui.

Soit $n$ un entier naturel non nul.
Soit $E$ un ensemble de $n+1$ nombres entiers distincts compris entre 1 et $2n$.
Démontrez qu'il existe deux entiers $p$ et $q$ de $E$ tels que $p|q$.

Code de déblocage de la correction :

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲