Formation python 2022

Les scripts, les fonctions

Programme informatique qui ne nécessite pas de compilation avant d'être exécuté. Pour fonctionner, les scripts doivent être interprétés par un programme ou un serveur dédié au langage dans lequel ils ont été écrits.

import

A partir de cette section, vous devez écrire vos programmes dans l'espace des scripts et utiliser le symbole pour exécuter vos programmes.

Importation systématiques des librairies utiles et encodage:

On peut ainsi utiliser directement les fonctions mathématiques et aléatoires de base ainsi que faire des graphiques avec une syntaxe aussi légère que possible tout en étant compatible avec la littérature sur le sujet. La ligne avec coding: utf-8 -*- permet d'éviter des soucis avec les caractères accentués.

Commencer tous vos programmes par cette série d'imports :

# -*- coding: utf-8 -*-
from math import * 
from random import *
import matplotlib.pyplot as plt
import numpy as np

Les fonctions

En Python une fonction est définie par l'instruction composée def suivie du nom de la fonction et se termine obligatoirement par deux points : puis le bloc d'instructions qu'il ne faut pas oublier d'indenter.

Une fonction est utilisée comme une instruction quelconque. Dans le corps d'un programme, un appel de fonction est constitué du nom de la fonction suivi de parenthèses.

La notion de fonction en informatique relève du même concept qu'une fonction mathématiques, c'est-à-dire qu'on définit une fonction puis on l'applique à différentes valeurs.

def carree(a) :
	" "" Fonction permettant de renvoyer le carré du nombre a qui est en paramètre "" "
	return a**2 # renvoie l'image de a par la fonction carree

Vous remarquerez le symbole : très important en Python qui marque le début d'un bloc.

C'est l'indentation qui délimite le bloc d'instructions.

Lorsqu'on définit la fonction carree(), a est appelé paramètre de la fonction. Lorsqu'on appelle la fonction avec une valeur explicite pour a, comme dans carree(3), on dira plutôt que 3 est un argument de la fonction.

En appelant la fonction carree() d'argument 3, on obtient 9

La fonction est autodocumentée par un texte : " "" Ecrire ici la description "" " (c'est ce que l'on appelle le docstring de la fonction).

Le docstring d'une fonction permet de donner des informations sur la fonction et le lien entre les entrées et la sortie (en d'autres termes, le rôle de la fonction).

Quant on saisit dans la console, après l'exécution de la fonction, l'instruction help(nom de la fonction), Python affiche le docstring de la fonction ce qui nous permet d'avoir des informations sur la fonction en cas d'oubli.
```
>>> help(carree)
		Help on function carree in module __main__:
	
			carree(x)
				Fonction permettant de renvoyer le carré
				du nombre x qui est en paramètre
```
La fonction se termine avec une instruction return. Ce qui suit le return est l'image des entrées par la fonction. Dès que la fonction rencontre un return, elle renvoie ce qui suit le return et stoppe son exécution.

Commentaire : le symbole # apparaîtra à maintes reprises. Il marque le début d’un commentaire que la fin de la ligne termine. Autrement dit, un commentaire est une information aidant à la compréhension du programme mais n’en faisant pas partie.

Différence entre fonction et procédure.

Une fonction renvoie une valeur et une procédure ne renvoie rien. Le langage Python ne fait pas la différence entre les deux, il utilise l'instruction def pour les deux. Par contre l'instruction return n'est pas obligatoire dans le cadre d'une procédure.

Il est conseillé d'écrire return None dans le cadre d'une procédure, mais ce n'est pas une obligation.

Tester le programme suivant :

def affichage(mot1,mot2):
    print(mot1,mot2)
    

affichage("maths ","Python ")

Transformer cette procédure en ajoutant return None à la fin de la fonction affichage . Tester la procédure.

Chercher l'erreur ( il y a une erreur à corriger).

def carre(x):
return x**2 
    
print(carre(1.7))

Chercher l'erreur ( il y a une erreur à corriger).

def quotient(x,y)
    return x/y

Ecrire une procédure qui prend en entrée deux variables nb1 et nb2 et qui affiche la moyenne des deux variables.

Ecrire une fonction moyenne(nb1,nb2) qui a pour paramètres deux variables de type float et qui renvoie la moyenne de ces deux nombres.

Ecrire une fonction vitesse(d,t), qui a pour paramètres deux variables de type float correspondant la distance d en mètre et le temps de parcours t en seconde et qui renvoie la vitesse en m/s.

Limiter les variables intermédiaires

Utiliser une écriture qui correspond aux notations mathématiques $$f:x \mapsto 2x+3$$ Limiter le recours aux variables intermédiaires c'est utiliser davantage la notation fonctionnelle qui correspond aux notations du cours de maths
```
# Au lieu d'utiliser cette forme :
def f1(a,b):
	c=a**2+b**2
	return c

# Utiliser cette forme
def f(a,b):
	return a*a+b*b
```
Privilégier une version fonctionnelle à une version procédurale.

Un grand classique : les racines d'un trinôme.

Les structures conditionnelles

Un programme doit souvent prendre en compte différents cas et s'adapter à différentes situations.

Il est alors nécessaire d'écrire des conditions, c'est-à-dire des expressions logiques dont le résultat est soit "Vrai " soit "Faux ".

Voici comment s'écrit la structure conditionnelle en python :

if condition :
	instruction(s)
else :
	instruction(s)

Vous remarquerez le symbole : très important en Python qui marque le début d'un bloc.

C'est l'indentation qui délimite le bloc d'instructions

Dans le cas où la condition est fausse, on peut donner des instructions à l'aide de la commande else .

def egaliteFrac(frac1,frac2):
	nb1 = frac1[0]*frac2[1]   #on calcule a*d
	nb2 = frac1[1]*frac2[0]   #on calcule b*c
	if nb1 == nb2:
		test = True
	else:
		test = False
	return test

egaliteFrac([1,2],[-20,-40])

La structure elif :

if condition1 :
	instruction(s)
elif condition2 :
	instruction(s)
elif condition3 :
	instruction(s)
else :
	instructions


a=float(input("Entrer un nombre : "))
if a>0 :
	print("Vous avez entré un nombre strictement positif. ")  
elif a==0 :
	print("Vous avez entré un nombre nul. ")
else :
	print("Vous avez entré un nombre strictement négatif. ")

Il est possible d'utiliser plusieurs conditions en utilisant les connecteurs logiques AND et OR.

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=|x-3|$.

Ecrire une fonction f(x) qui prend en paramètre une variable de type float et qui renvoie un objet de type float correspondant à l'image de $x$ par $f$.

On n'utilisera pas la fonction abs(x) correspondant à $|x|$.

Abonnement et réseau social

Niveau : accessible

Inspiré du programme de SNT

" Un abonnement sur un réseau social de vidéo coûte 9.99 € par mois avec trois mois d 'essai gratuit pour une seule personne ou 15.99 € avec 1 mois d'essai gratuit pour toute la famille ".

Compléter la fonction suivante qui a pour argument le nombre de mois et qui renvoie le prix à payer.


def prix(mois):
	abonnement=input("Abonnement ? : seul ou famille ? ")
	# faire afficher "abonnement minimal d 'un an" si le nombre de mois est inférieur à 12
	# ...
	return(prix)

Tester la fonction avec :


print(prix(12))

Vous devriez observer :

Abonnement ? : seul ou famille ? seul 89.91

Une vidéo qui donne offre une autre présentation :

Les boucles bornées - for

La boucle pour est utilisée quand on connaît le nombre de fois où l'on doit répéter une suite d 'instructions.

Parcours sur les index

Dans un premier temps l'attribut dans range sera un entier, nous verrons dans la suite qu'il peut en être autrement.


for i in range(n):
	...
	les différentes instructions à répéter 
	...

Il y a ainsi trois possibilités pour utiliser l'instruction range, suivant le nombre de paramètres entiers saisis :

```
for i in range(n):
```
le compteur $i$ va de 0 à $n-1$ par pas de 1 : il y a donc bien $n$ répétitions.
```
for i in range(m,n):
```
le compteur $i$ va de $m$ à $n-1$ par pas de 1 : il y a donc $n-m$ répétitions. Ici, on a forcément $n\geq m$.
```
for i in range(m,n,pas):
```
le compteur $i$ va de $m$ à $n-1$ par pas de $pas$ ; le pas est un entier relatif non nul, il peut en particulier être négatif.

Pour illustrer cette structure nous allons partir sur un premier exemple : obtenir la somme des n premiers entiers naturels. Pour n=4, on veut écrire un programme qui renvoie la valeur de 0+1+2+3=6.

La première ligne fait que la suite du code va être répétée n fois en incrémentant de manière automatique la variable i de 0 à n-1.


def somme(n): #les int sont ici pour indiquer le typage des variables d'entrée et de sortie. Ici l'attribut est de type int et la sortie également   
    """""La fonction somme renvoie la somme des n-1 premiers entiers naturels.
    la fonction somme a pour attribut un entier (int) : n et renvoie un autre entier :S
    Pour n=4 : S=0+1+2+3=6""""" 
    S=0 #initialisation de la somme à 0
    for i in range(n): 
        S=S+i
    return S
somme(4) # Penser à faire un print(somme(4)) si vous voulez un affichage

Pour voir l'exécution du code, un site intéressant : "python tutor" (abordé un peu plus loin sur le site)

Pour l'utiliser dans capytale :

from tutor import tutor
import math

def termes(n):
    #version for
    u=0.5
    l=[0.5]
    for i in range(n):
        u=math.sqrt(1+u)
        l.append(u)
    return l
termes(10)
tutor()

On donne une suite $u_{n}$ définie par sa relation de récurrence :

$\left\{ \begin{array}{ll} u_{n+1} = \frac{u_n + 1}{u_n-2}\\ u_0=1 \end{array} \right.$

Ecrire une fonction u(n) qui a pour argument une variable n de type int et qui renvoie le terme d'indice $n$ de la suite $u$.

Parcours sur les éléments

Dans la partie précédente, l'instruction range(m,n) créé un ensemble de nombres dont le compteur i parcourait les valeurs.

Un tel ensemble dont un peut parcourir les valeurs avec une boucle for est appelé un itérable.

Il existe de nombreuses structures de données itérables :

Une chaîne de caractères (type str) est un itérable,
Une liste (type list) est un itérable,
Un dictionnaire (type dict) est un itérable (abordé dans la formation python 2),

En Python, pour utiliser un itérable dans une boucle for, il suffit d'utiliser le mot-clé in. Voici la structure générale :

for elt in iterable:
    instruction 1
    instruction 2
    ...

Dans cette boucle, elt va parcourir les éléments de la iterable.

Le programme ci-dessous affiche séparément chaque caractère d'une chaîne de caractères :

# -*- coding: utf-8 -*-
ch="Bonjour à tou.te.s"
for elt in ch:
    print(elt)

Le but est compter le nombre de 'e' dans une phrase.


def nbre_de_e(phrase):
    compteur=0
    for lettre in phrase:
        if lettre=="e":
            compteur=compteur+1
    return compteur

print("Le nombre de e est :",nbre_de_e("hello world!"))

Transformer l'algorithme pour qu'il compte le nombre de voyelles.

Simulation du lancer d'un dé

from random import randint # on importe le module randint de random
liste=[randint(1,6) for i in range(1000)]
print(liste)

Utiliser le code de l'exercice précédent pour compter le nombre de 1 de la liste.

Une vidéo sur les boucles for :

Les boucles non bornées - while

Ces boucles, aussi appelées boucles "Tant que" ou boucles "While" effectuent les instructions situées dans le corps de la boucle tant qu'une condition est vérifiée. En langage Python, la syntaxe est la suivante :


	while condition_est_vraie:
		instruction 1
		instruction 2

A l'instar des structures conditionnelles (si alors sinon) et des boucles bornées (pour), le corps de la boucle est constitué d'instructions indentées.

Cas général : nombre d'itérations non connu :

On utilise cette boucle lorsque l'on ne sait pas à l'avance combien de fois seront effectuées les instructions du corps de la boucle. Cela peut être lié à la valeur d'une ou de plusieurs variables dont la valeur évolue, parfois à cause de la décision de l'utilisateur.

Les suites offrent de nombreuses situations.

Algorithme de seuil

On donne une suite $u_{n}$ définie par sa relation de récurrence :

$\left\{ \begin{array}{ll} u_{n+1} = 3u_n + 1\\ u_0=2 \end{array} \right.$

On cherche l'indice $n$ tel que $u_{n} \ge 300 $

On a l'algorithme en pseudocode suivant :

u ← 0
n ← 0
tant que u < 300 faire
	n ← n+1 
	u ← u+1

Cet algorithme donne le programme suivant :

from math import *
u=0
n=0
while u <300:
	n=n+1
	u=3*u+1

print(n, u)

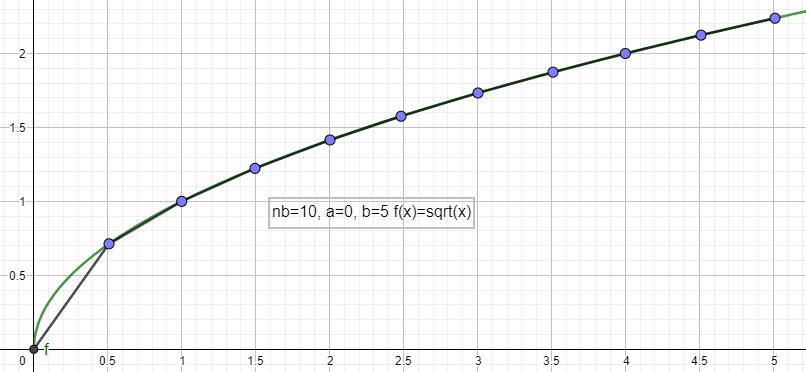
Longueur de courbe

Pour obtenir l'approximation de la longueur d'une courbe représentative d'une fonction $f$ sur un intervalle $[a;b]$. On peut découper $[a;b]$ en $n+1$ intervalles et ajouter les longueurs des $n+1$ segments d'extrémitées $A(x_n,f(x_n))$ et $B(x_{n+1},f(x_{n+1}))$

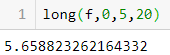
Ecrire une fonction long(f,a,b,nb) qui renvoie l'approximation de la longueur de la courbe représentative de $f$ sur l'intervalle $[a;b]$ avec nb intervalles.

Une vidéo de présentation des boucles while :

Et une autre :

Aspect général de jupyter

Un aperçu d'un fichier jupyter.

Observer le déroulement d'un programme en Python

Pour observer l’exécution d’un programme, nous pouvons utiliser une application web : pythontutor

Une vidéo présentant le fonctionnement de pythontutor :

▲