Quelques exemples de programmes
Vous pouvez vous rendre dans l'espace python1 pour voir les exemples de programmes proposés :
- Algorithme de dichotomie
- Le jeu des 8 erreurs
- Jeu inspiré de l'algorithme de dichotomie.
- Transformer une version procédurale en fonctionnelle : second degré
- Ensemble de fonctions : périmètre et aire (avec productions d'élèves)
- Ensemble de fonctions : géométrie analytique (avec productions d'élèves)
- Représenter une fonction
- Créer et importer sa propre bibliothèque
- La bibliothèque turtle pour faire des dessins
Une approximation de pi
L'idée ici pour obtenir une approximation de pi est de créer des points au hasard dans un carré de coté 2 et de compter ceux qui se trouvent dans un disque de rayon 1 inscrit dans le carré.
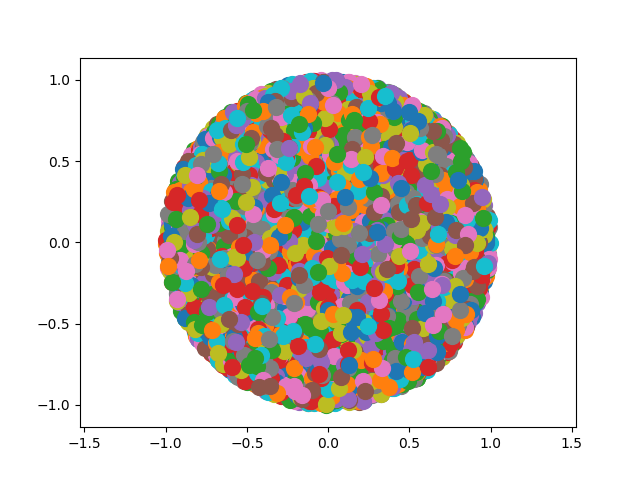
Pour cela on peut utiliser l'instruction random qui renvoie un nombre aléatoire entre 0 et 1. (Shift Entrée pour exécuter les blocs de code
A l'aide de la random() du module random écrire une fonction
pointAleatoire()renvoyant les coordonnées d'un point aléatoires et dans l'intervalle [-1;1].Créer une fonction
estDansLeDisque(xA,yA)renvoyant un booleen : True si le point A est dans le disque unité et False sinon.Ecrire une fonction
compteurAffiche(n)qui renvoie le nombre de points du disque unité parmis n points lancés aléatoirement dans le carré et qui affiche les points dans le disque.
Ecrire une fonction demo() qui demande à l'utilisateur le nombre de points voulu pour l'approximation, qui affiche l'approximation obtenue ainsi que le nombre de points dans le disque et qui affiche l'ensemble des points dans le disque. On pourra ajouter le tracé du cercle et du carré avec le module numpy.
Une autre approximation de pi
Une autre façon d'obtenir une approximation de $\pi$ est de considérer le quart du disque unité et de le découper en rectangle et d'ajouter la surface de chaque rection pour obtenir une approximation de $\pi$.
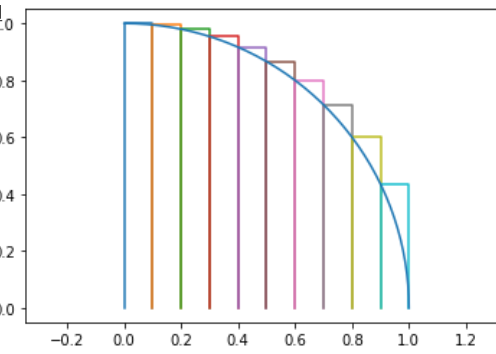
Ecrire une fonction pi_rect(n) qui renvoie une approximation de $\pi$ à partir de n rectangles et qui affiche une représentation du quart de cercle et des rectangles.
Suites imbriquées
On considère les suites $(x_n)$ et $(y_n)$ définies par $x_0=1$, $y_0=8$ et pour tout entier naturel $n$ :
$$\left \{ \begin{array}{l} x_{n+1} = \frac73x_n+\frac13y_n+1 \\ y_{n+1} = \frac{20}3x_n+\frac83y_n+5 \\ \end{array} \right. $$
Ecrire une fonction suites(n) qui affiche une liste des couples $(x_i;y_i)$ pour $i\leq n$ et qui propose une représentation de ces points.
Complexe et Python
Voici un exemple d'exercice proposé aux élèves de l'option mathématiques expertes.
$(0 ; \vec{u},\vec{v})$ est un repère orthonormé direct du plan complexes.
Pour la figure, on pendra pour unité 5 cm.
On considère la suite $(z_n)$ définie par $\left\{ \begin{array}{l} z_0=0\\ z_{n+1}=\dfrac{1}{2}(1+i) z_n-1+i \textrm{, pour tout } n\in\mathbb{N} \end{array} \right.$
Pour tout entier naturel $n$, on note $M_n$ le point du plan complexe qui a pour affixe $z_n$
-
-
Déterminer la forme algébrique de $z_1$ , $z_2$, $z_3$ et $z_4$.
-
Placer, dans le plan complexe, les points $M_0$, $M_1$ , $M_2$, $M_3$ et $M_4$.
-
-
Voici une fonction Suite_1 écrite dans le langage Python.
- Saisir cette fonction et l'exécuter pour $n=1$, $n=2$, $n=3$ et $n=4$. Quels rsultats retrouve-t-on ainsi ?
- Utiliser cette fonction pour obtenir $z_5$ , $z_6$, $z_7$ et $z_8$.
-
Placer, dans le plan complexe, les points $M_5$, $M_6$ , $M_7$ et $M_8$.
- $(Z_n)$ est la suite définie sur $\mathbb{N}$ par $Z_n=z_n+2$.
- Quel est le vecteur dont l'affixe est $Z_n$ ?
- Montrer que pour tout $n\in\mathbb{N}$, $Z_{n+1}=\dfrac{1}{2}(1+i)Z_n$.
- Déterminer $Z_0$.
- Ecrire en langage Python, une fonction Suite_2 qui, pour une valeur $n$ du paramètre renvoie le nombre complexe $Z_n$.
- Saisir ce programme à l'aide de cette fonction, conjecturer une propriété des nombres $Z_{4k}$ et $Z_{4k+2}$, pour $k$ nombre entier naturel.
-
- Démontrer que pour tout entier naturel $n$, $Z_n=\dfrac{(1+i)^n}{2^{n-1}}$. En déduire l'exprerssion de $z_n$ en fonction de $n$.
- Démontrer que pour tout entier naturel $k$, $(1+i)^{4k}$ est un nombre réel et $(1+i)^{4k+2}$ est un imaginaire pur. Que peut-on en déduire pour les points $M_{4k}$ et $M_{4k+2}$ ?
from cmath import *
def Suite_1(n):
z=0
for i in range(1,n+1):
z=(1+1j)/2*z-1+1j
return z cmath pour travailler avec les nombres
complexes.
Les complexes se notent : 1+1j, 3j, -1+0j, ...
Ecrire l'expression de $Z_{n+1}$ et mettre $1+i$ en facteur.
Exécuter ce programme pour des paramètres de la forme $4k$ et $4k+2$.
- Démontrer que pour tout entier naturel $n$, $|Z_n|=2\times\left(\dfrac{\sqrt{2}}{2}\right)^n$
- Quelle est la limite de la suite $(|Z_n|)$ lorsque $n$ tend vers $+\infty$.
- Interpréter géométriquement ce résultat.
Simulation d'une variable aléatoire
Une animation avec Python
Fluctuation des fréquences de succès. Animation tirée de l'espace Eduscol.
Ressources n°8 d'Eduscol
Statistiques à deux variables
Faire des regressions linéaires en STS en utilisant python.
Le fichier jupyter à télécharger iciDes exemples sur les graphes
Un ensemble d'exemples utilisant la biblithèque networkx.
Le fichier jupyter à télécharger iciFaire du calcul formel avec python
Vous pouvez utiliser la bibliothèque SimPy pour faire du calcul formel.
Vous avez un tutoriel de la bibliothèque avec une console pour faire vos tests : Accès direct
Vous pouvez retrouver également dans le jupyter cidessous quelques exemples :
Le fichier jupyter à télécharger iciEtude d'une marche aléatoire
Cet exemple utilise un utilitaire de représentation des graphes qui s'appelle grahviz.
Une vidéo pour l'utilisation de cet utilitaire :
Le fichier jupyter à télécharger ici Le fichier dirmaths à télécharger ici