Voici différents couples d'exercices qui sont à traiter chacun en environ 55 minutes
et où vous pouvez utiliser les logiciels Geogebra et Xcas.
Faire l'effort de rédiger les réponses comme pour un devoir, d'expliciter les formules de cours utilisées.
Ne pas hésiter à m'appeler en cas de questions ou de vérifications nécessaires ; penser sinon à réaliser des captures d'écran
des calculs et démarches effectués sur ces deux logiciels.
Compétences à maîtriser pour le CCF
Vous trouverez dans le document suivant l'ensemble des compétences à maîtriser pour le CCF :
Couple 1
Premier exercice du couple 1
Une entreprise de service informatique vient de finaliser un site commercial pour un grand groupe hôtelier.
Des bugs sont rencontrés au cours des premier jours de mise en ligne du site.
Les interventions sont étudiées.
Partie A. Étude statistique du nombre d'interventions
Une entreprise de service informatique vient de finaliser un site commercial pour un grand groupe.
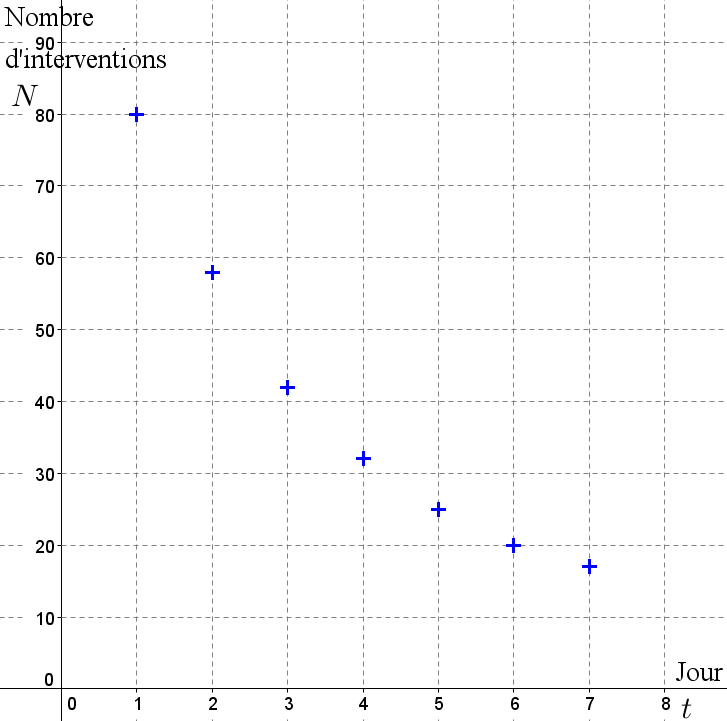
Le nombre d'interventions sur les 7 premiers jours a été relevé. Les données sont représentées sur le graphique
ci-dessous :
-
Au vu de la représentation graphique obtenue, un ajustement affine semble-t-il approprié ? Expliquer.
-
On désigne par $N$ le nombre d'interventions, et on pose : $y=\ln(N-10)$.
Les données mesurées sont données ci-dessous :Jour étudié $t$ 1 2 3 4 5 6 7 Nombre d'interventions $N$ 80 58 42 32 25 20 17 $y$ 4.2485 3.8712 3.4657 ... 2.7081 2.3026 1.9459 -
Dans le tableau, quelle est la valeur manquante $y$, arrondie au millième, correspondant au quatrième jour ?
-
Déterminer une équation de la droite d'ajustement de $y$ en $t$, par la méthode des moindres carrés. Arrondir les coefficients au dix-millième.
-
Déterminer le coefficient de corrélation linéaire arrondi au dix-millième.
Que pouvez-vous déduire de ce coefficient ? (Deux informations attendues) -
Déduire de l'ajustement de $y$ en $t$ un ajustement de $N$ par $t$.
-
Utiliser l'ajustement de $N$ par $t$ pour estimer le nombre d'interventions nécessaires le neuvième jour ($t=9$).
-
En utilisant l'ajustement de $N$ par $t$, estimer quel jour il y aura 11 interventions.
-
En utilisant l'ajustement de $N$ par $t$, l'entreprise peut-elle espérer ne plus avoir à intervenir au bout d'un certain temps ? Justifier.
-
Partie B. Étude probabiliste du temps de correction des bugs
Le grand groupe client envoie un mail ou téléphone à chaque bug rencontré.
Dans cette partie le but est d'étudier le temps d'attente entre l'information du bug et le temps de correction de celui-ci.
On considère que chaque bug est indépendant des autres.
On appelle $T$ la variable aléatoire qui à chaque annonce de bug associe le temps en minutes de la correction de celui-ci.
On admet que la variable $T$ suit une loi exponentielle de paramètres $\lambda=0.02$.
-
Déterminer la probabilité que le bug soit réglé en moins d'une heure et demie.
-
Déterminer le temps moyen nécessaire pour corriger un bug.
Second exercice du couple 1
Partie A : équation différentielle
Le pourcentage du niveau d'insatisfaction suite à la mise en place du nouveau site au bout de $x$ jours est donné par $f(x)$ où $f$ est solution de l'équation différentielle $(E) : 5y'+y=5+100\times e^{-\frac{1}{5}(x+1)}$, avec $f(0)=20$, où $y$ désigne une fonction dérivable sur $[0 ; +\infty[$ et $y'$ sa fonction dérivée.
-
Déterminer à la main les solutions de l'équation différentielle : $(E_0)$ $5y'+y=0$.
-
Soit $g$ la fonction définie sur $[0;+\infty[$ par $g(x)=20x \exp\left(-\dfrac{x+1}{5}\right)+5$.
Démontrer que $g$ soit une solution de l'équation différentielle $(E)$. -
En déduire la forme de toutes les solutions de l'équation différentielle $(E)$.
-
Initialement, lorsque $x=0$, $20$% des clients sont insatisfaits.
Déterminer la fonction $f$ donnant le pourcentage d'insatisfaction des clients en fonction du nombre de jours $x$ écoulés depuis la mise en place du nouveau site. -
Vérifier, grâce à Xcas, la fonction $f$ qui est solution de $(E) : 5y'+y=5+100\times e^{-\frac{1}{5}(x+1)}$ telle que $f(0)=20$.
Partie B : étude de fonction
On admet que le pourcentage de clients insatisfaits après $x$ jours de mise en place du nouveau site est donné par $f(x)=15\times exp\left(-\dfrac{x}{5}\right)+20x\times exp\left(-\dfrac{x+1}{5}\right)+5$
-
Quel sera le taux d'insatisfaction du site à très long terme ?
-
Prouver que $f'(x)=\left(\left(20-4x\right)\times \exp\left(-\dfrac{1}{5}\right)-3\right)\times \exp\left(-\dfrac{x}{5}\right)$.
-
Dresser le tableau de variations complet de $f$ sur $[0;+\infty[$.
-
En déduire le jour où le taux d'insatisfaction est maximum ainsi que la valeur de ce taux.
-
Quel sera le taux d'insatisfaction moyen sur les 10 premiers jours ?
Couple 2
Premier exercice du couple 2
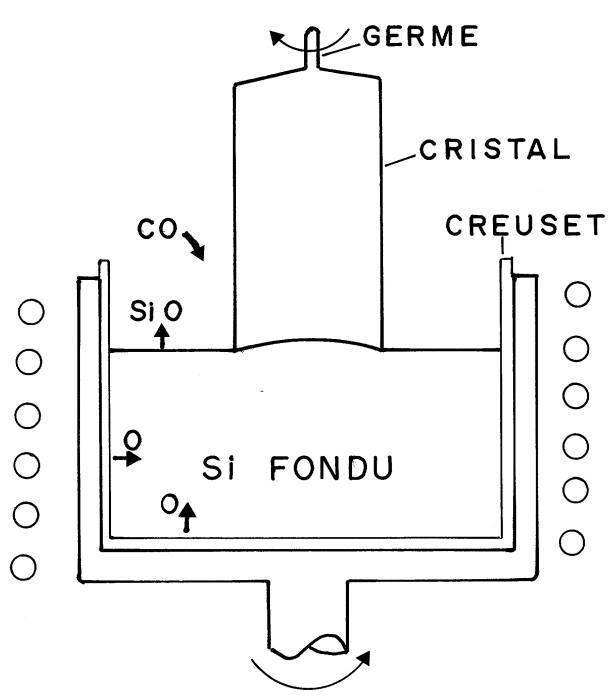
Une entreprise crée des monocristaux de silicium à partir de la silice fondue dans un four
afin de créer des barres cylindriques de monocristaux de silicium par tirage en suivant la
méthode de Czochralski.
Pour obtenir un monocristal, d’orientation donnée, ne contenant
aucune dislocation, un petit morceau de silicium ayant ces caractéristiques, appelé germe, est mis en contact avec le silicium liquide
fondu dans un creuset. Ce germe
imposera son orientation cristallographique lors de la solidification.
Pour une bonne homogénéisation de la température, le creuset et le cristal sont animés de mouvements de rotation
continus en sens inverses, tandis que le germe est tiré vers le haut.
Le cristal obtenu sera ensuite découpé en tranche fine : des wafers. Ces wafers sont
par la suite gravés pour obtenir des puces de processeurs.
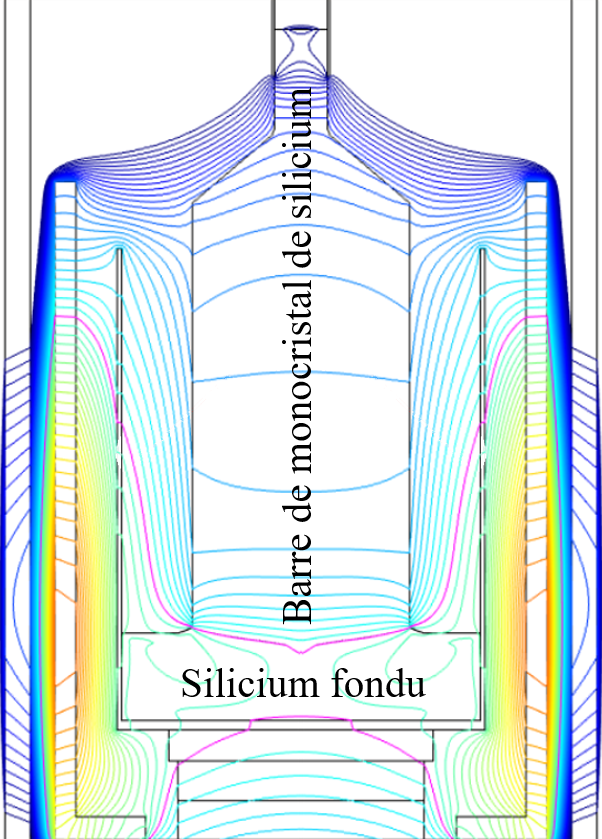
Lignes de niveau des températures internes au four
La température du cylindre au-dessus du creuset où le silicium est en fusion doit être précisément
gérée de sorte que le monocristal de silicium soit d'une très grande pureté.
Pour cela, le four doit être conçu très précisément.
Suite à une modification d'un nouveau four expérimental, un test est réalisé et les mesures suivantes
ont été obtenues :
| Température $t_i$ (en °C) | 1320 | 1338 | 1350 | 1358 | 1363 | 1370 | 1380 | 1387 | 1393 | 1402 | 1410 | 1420 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distance $d_i$ (en mm) | 10 | 50 | 150 | 250 | 400 | 700 | 1100 | 1500 | 1700 | 1900 | 2000 | 2100 |
Dans ce tableau :
-
$t_i$ représente la température du centre de la barre de silicium mesurée par une sonde.
-
$d_i$ représente la distance entre la sonde et le sommet du four en millimètres.
-
À l'aide de Geogebra, justifier qu'un ajustement affine de $d$ en $t$ n'est pas approprié.
-
Afin de mieux modéliser cette série statistique, on effectue les deux changements de variable : $x=t-1300$ et $z=\ln\left(\dfrac{2150}{d}-1\right)$.
On obtient suite à ce changement de variables le tableau de valeurs incomplets ci-dessous :$x_i$ 20 38 50 58 63 70 80 87 93 102 110 120 $z_i$ 5.366 3.7377 2.5903 2.0281 ... 0.7282 -0.0465 -0.8362 -1.3291 -2.0281 -2.5903 -3.7377 -
Déterminer la valeur manquante pour $z_i$ dans le tableau ci-dessus.
-
Calculer le coefficient de corrélation linéaire de la série statistique $(t_i ; z_i)$.
-
Expliquer pourquoi un ajustement affine de cette série est pertinent.
-
Donner une équation de la droite de régression de $z$ en $x$ selon la méthode des moindres carrés, sous la forme $z=ax+b$, où $a$ et $b$ sont arrondis à $10^{-4}$.
-
-
Désormais, on considère que $z=-0.09 x +7.15$.
Démontrer en utilisant les changements de variables liant $x$ et $t$ ainsi que $z$ et $d$ que l'on peut déduire de l'ajustement affine $z=-0.09 x +7.15$, l'ajustement logistique suivant : $d=\dfrac{2150}{1+1274\times e^{-0.09(t-1300)}}$.
-
La surface en fusion du silicium dans le creuset est à une température de $1425$ °C.
À quelle distance du sommet du four, se trouve cette surface en fusion ?
Deuxième exercice du couple 2
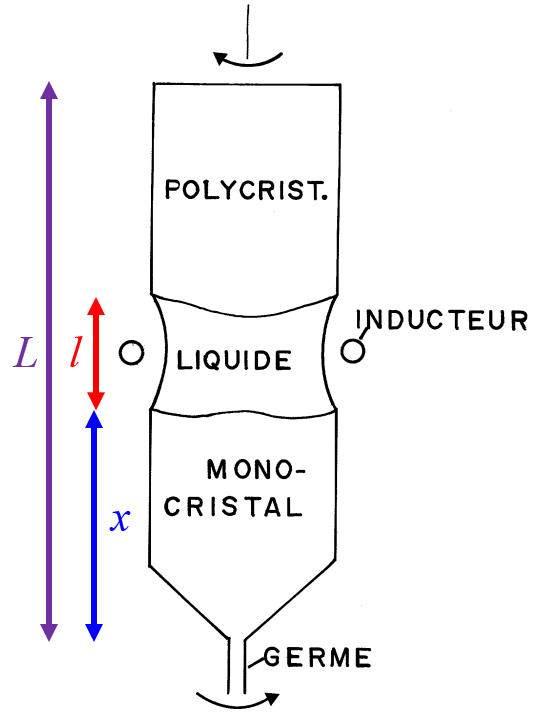
L'entreprise teste une seconde méthode pour créer des monocristaux de silicium : la méthode de la
zone flottante.
Cette méthode permet d’obtenir du silicium d’une plus grande pureté en évitant la contamination
par le creuset. Le processus consiste à produire une zone liquéfiée en chauffant, par induction,
un bâton de silicium polycristallin.
Le bâton est déplacé verticalement en suivant une lente rotation.
Le carbone est une impureté présente dans les polycristaux de silicium dont il faut réduire la concentration pour une utilisation du cristal dans la réalisation de puces électroniques.
La liquéfaction permet de réduire la concentration en impuretés dans le monocristal de silicium obtenu par rapport au taux d'impuretés dans le polycristal de silicium initial.
On note $L$ la longueur totale du bâton en mètre, $l=0.03$ la largeur de la zone fondue par induction et $x$ la longueur du bâton de silicium monocristallin déjà obtenu.
On suppose que le barreau initial polycristallin a une concentration homogène en impureté de carbone. Cette concentration est ici supposée valoir $10^{-8}$.
On appelle $f$ la fonction, définie sur $[0 ; L-l]$ donnant la concentration, en $10^{-9}$, des impuretés de carbone
dans le bâton monocristallin à une hauteur $x$, exprimée en mètres.
On admet que $f$ est solution de l'équation différentielle suivante $(E)$ :
$0.5y'+y=10$ avec $f(0)=0.6$, où $y$ désigne une fonction dérivable sur
$[0 ; L-l]$ et $y'$ sa fonction dérivée.
-
Déterminer à la main les solutions de l’équation différentielle : $(E_0)$ $0.5y'+y=0$.
-
Soit $g$ la fonction définie sur $[0;+\infty[$ par $g(t)=C$, où $C$ est une constante réelle.
Déterminer la valeur que doit prendre $C$ pour que $g$ soit une solution de l'équation différentielle $(E)$. -
En déduire la forme de toutes les solutions de l'équation différentielle $(E)$.
-
À une distance $x=0$ (début du bâton monocristallin), la concentration en impuretés de carbone est de $0.6$ (en $10^{-9}$).
Déterminer la fonction $f$ donnant la concentration en impuretés de carbone en fonction de $x$ (en mètres) vérifiant cette condition initiale. -
Vérifier, grâce à Xcas, la fonction $f$ qui est solution de $(E) : 0.5y'+y=10$ telle que $f(0)=0.6$.
-
On considère la fonction $p$ définie sur $[0;+\infty[$ par $p(x)=100-94\times e^{-2x}$.
On admet que cette $p(x)$ donne la concentration, en $10^{-10}$, des impuretés de carbone dans le bâton de silicium monocristallin au bout de $x$ mètres.-
Déterminer la concentration en impuretés de carbone au bout de $10$ centimètres.
-
Le cristal monocristallin est jugé suffisamment pur lorsque la concentration en carbone est inférieure à $50\times 10^{-10}$.
Déterminer la longueur maximale que l'on peut utiliser dans le cristal monocristallin pour qu'il soit jugé entièrement suffisamment pur. Arrondir au millimètre près.
-
Couple 3
Premier exercice du couple 3
Un filtre passe-bas est modélisé par un circuit composé d'une résistance et d'un
condensateur en série.
On note :
-
$e(t)$ est la tension aux bornes du circuit, exprimée en volt, à l'instant $t$ (en seconde).
Dans tout cet exercice, on suppose que le circuit est alimenté par une tension constante : $e(t)=3$, si $t\ge 0$.
-
$s(t)$ est la tension aux bornes du condensateur, exprimée en volt, à l'instant $t$ (en seconde).
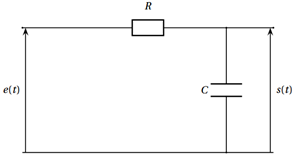
À l'instant $t=0$, le condensateur est déchargé et on a : $s(0)=0$.
On admet que l'application des lois de la physique conduit, pour tout $t > 0$,
à la relation : $4s'(t)+s(t)=3 (E)$.
Les parties A et B peuvent être traitées indépendamment.
Partie A : traitement analogique
-
À la main, résoudre l'équation différentielle homogène $4s'(t)+s(t)=0$.
-
En utilisant Xcas, déterminer, pour tout nombre réel $t$ positif ou nul, l'expression de $s(t)$, où $s$ est la fonction causale vérifiant l'équation différentielle $4s'(t)+s(t)=3 (E)$ telle que $s(0)=0$.
-
Déterminer la valeur du nombre réel $L$, limite de $s(t)$ quand $t$ tend vers $+\infty$.
-
On appelle temps de réponse du système la valeur du nombre réel $t$ à partir de laquelle $s(t)$ atteint 95% de la valeur de la limite $L$ calculée à la question précédente 3.
Déterminer une valeur approchée, à 0.1 seconde près, du temps de réponse du système.
Partie B : traitement numérique
On s'intéresse maintenant à un filtre passe-bas numérique destiné à approcher le filtre
analogique étudié dans la partie A.
Une discrétisation de l'équation différentielle $(E)$ avec un pas de discrétisation $T_e$
permet d'obtenir, pour tout entier naturel $n$, la relation $(E')$ suivante :
$\dfrac{4(x(n+1)-x(n))}{T_e} +x(n+1)=3$.
On prend ici $T_e=0.5$ seconde.
Pour tout entier $n$, le nombre réel $x(n)$ donne une approximation de $s(nT_e)$.
En particulier, on a : $x(0)=s(0)=0$.
On admet que la relation $(E')$ peut s'écrire, pour tout entier positif ou nul,
sous la forme : $x(n+1)= \dfrac{8}{9} x(n)+ \dfrac{1}{3}$.
-
On a commencé à remplir le tableau de valeurs ci-dessous :
$n$
$0$
$1$
$2$
$3$
$4$
$x(n)$ $0$
$0.333$
$0.630$
$0.893$
$...$
Compléter ce tableau en calculant la valeur approchée à $10^{-3}$ près du nombre réel $x(4)$.
-
On admet que la suite $(x(n))$ tend vers $3$ lorsque $n$ tend vers $\infty$.
Le but est de déterminer le temps de réponse en secondes du système numérique.
Pour cela, vous devez compléter une des versions suivantes proposant de déterminer le premier entier naturel $n$ tel que $x(n)$ dépasse $95$% de la limite $3$.Version python :
n = ... x = ... # boucle répétitive ...: ... = ... ... = ... print("x(n) dépasse 95% de 3 à partir du rang n=", ...)Version pseudo-langage :
n ← ... x ← ... ... faire ... ← ... ... ← ... Fin_... Afficher("x(n) dépasse 95% de 3 à partir du rang n=", ...)Version C++ :
#include <iostream> using namespace std; int main(){ int n = ...; float x = ...; while (...){ ... = ...; ... = ...; } cout<<"x(n) dépasse 95% de 3 à partir du rang n="<<...<<endl; return 0; } -
On admet que les programmes suivants renvoie le nombre $26$.
En prenant en compte la période d'échantillonnage, déterminer le temps de réponse du système numérique en secondes.
Comparer avec le système analogique.
Second exercice du couple 3
Le taux d'utilisation d'un serveur en fonction du nombre de jours écoulés depuis le début du mois, commencé un samedi, est donné par le tableau suivant :
| Nombre $x$ de jours écoulés | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Taux $y$ d'utilisation du serveur | 78 | 57 | 32 | 20 | 31 | 56 | 77 | 77 | 58 | 33 | 20 |
-
Représenter le nuage de points $(x;y)$ sur Geogebra.
Que remarquez-vous quant à ce nuage de points en terme de régularité et d'alignement ? -
Parmi les ajustements proposés par Geogebra, lequel vous paraît le plus adapté pour réaliser un ajustement du nuage de points ?
-
On réalise le changement de variable suivant $z=\arcsin\left(\dfrac{y-50}{30}\right)$.
On obtient le tableau de valeurs suivant sur les quatre premières valeurs :Nombre $x$ de jours écoulés 0 1 2 3 $z=\arcsin\left(\dfrac{y-50}{30}\right)$ 1.14 0.24 -0.65 -1.55 -
Déterminer une équation de la droite de régression de $z$ en $x$, obtenue par la méthode des moindres carrés, sous la forme $z = ax + b$, où $a$ et $b$ sont à arrondir à $10^{-2}$.
-
En déduire une expression de $y$ en fonction de $x$, selon cet ajustement.
-
-
-
Déterminer sur Geogebra le tableau de valeurs donnant $z$ en fonction de $x$ lorsque $x$ varie entre 7 et 10.
-
Comparer les valeurs obtenues entre $a$ et $a'$ et entre $b$ et $b'$.
-
Justifier que l'écart obtenu entre $b$ et $b'$ n'a pas d'influence sur l'ajustement final de $y$ en $x$.
Déterminer une équation de la droite de régression de $z$ en $x$, obtenue par la méthode des moindres carrés, sous la forme $z = a'x + b'$, où $a'$ et $b'$ sont à arrondir à $10^{-2}$.
-
Couple 4
Premier exercice du couple 4
Vous travaillez dans une entreprise de mise en place et de gestion de réseaux informatiques.
Votre entreprise vient d'obtenir le chantier de relier par des fibres optiques quatre centres de serveurs.
Vous pouvez creuser et installer ces fibres partout où vous voulez dans la zone contenant les quatre centres,
nommés $A$, $B$, $C$ et $D$.
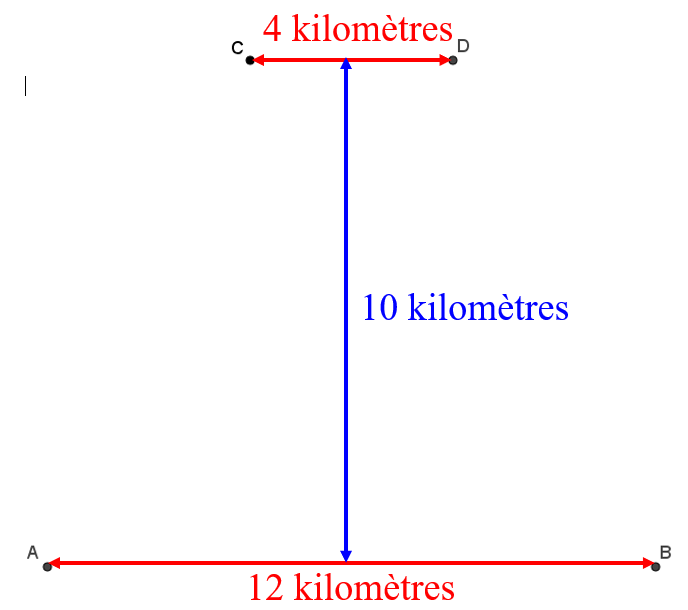
La première idée fut de relier directement en lignes droites les centres $B$, $A$, $C$ et $D$
comme montré sur la figure ci-contre.
On peut montrer qu'alors la distance totale de fibres optiques serait $2\sqrt{29}+16$, soit
environ $26.77$ kilomètres.
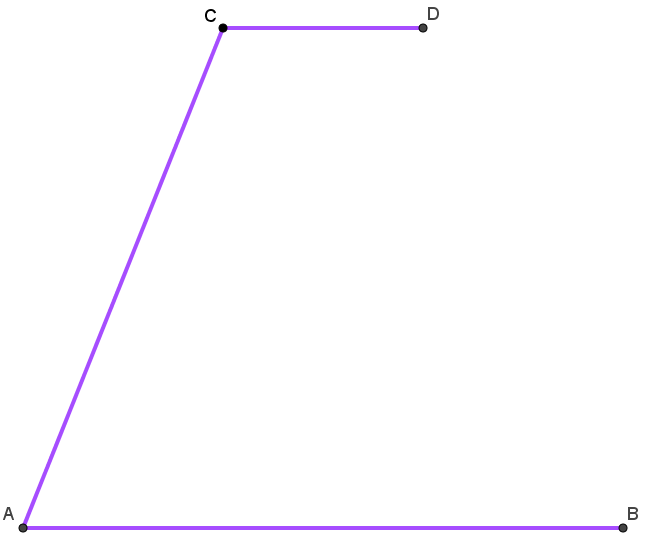
La première idée fut de relier directement en lignes droites les centres $A$, $C$, $D$ et $B$,
comme montré sur la figure ci-contre.
On peut montrer qu'alors la distance totale de fibres optiques serait $4 \sqrt{29}+4$, soit
environ $25.54$ kilomètres.
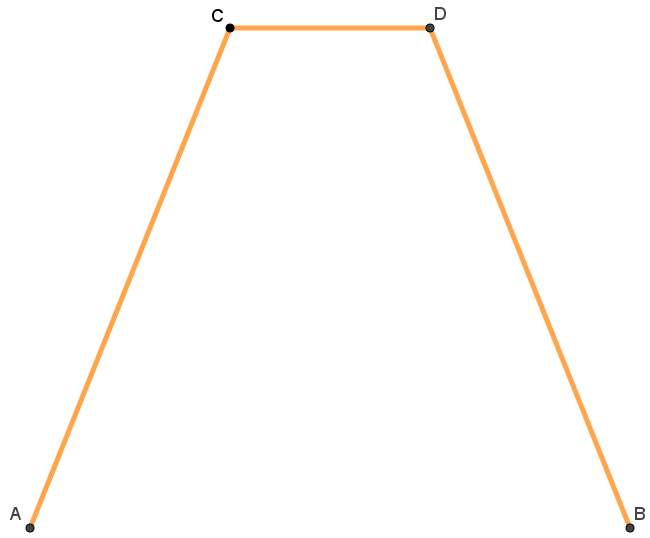
Si vous trouvez une configuration qui permet de réduire la distance totale de fibres
optiques à installer, votre entreprise vous propose une prime exceptionnelle correspondant à
5% de l'économie réalisée sur les travaux.
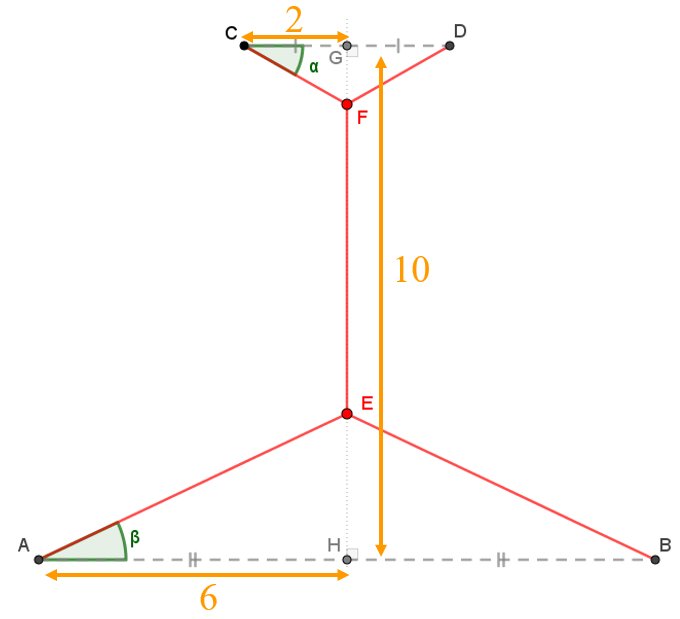
Vous avez l'idée de positionner deux centres intermédiaires $E$ et $F$ comme sur la figure ci-contre
de sorte que la longueur totale de fibres est donnée par la somme des longueurs : $Long=FC+FD+EF+AE+BE$.
Le but est de déterminer la valeur des angles $\alpha$ et $\beta$ telles que la longueur totale $Long$
soit minimale.
-
Exprimer la longueur $AE$ en fonction de la longueur $AH$ et de l'angle $\alpha$.
-
Déterminer le tableau de variations de $f$ sur $\left[0;\dfrac{\pi}{2}\right[$.
-
En déduire la valeur pour laquelle $f$ est minimale sur $\left[0;\dfrac{\pi}{2}\right[$.
-
En déduire la valeur que doivent prendre $\alpha$ et $\beta$ pour que la distance $Long$ soit minimale.
-
Chaque kilomètre de pose de fibre coûte 50000€.
Quel sera le montant de la prime offerte par votre entreprise ? Arrondir au centime près.
Dans toute la suite, on considère la fonction $f$ définie sur $\left[0;\dfrac{\pi}{2}\right[$ par $f(x)=\dfrac{2-\sin(x)}{\cos(x)}$.
On admet que la longueur totale $Long$ peut être donnée par l'expression $Long=10+2f(\alpha)+6f(\beta)$.
Second exercice du couple 4
Une fois l'installation réalisée, votre entreprise teste le temps de latence entre les deux serveurs $A$ et $D$ en fonction de la quantité d'information transmise entre les deux serveurs pour des flux TCP.
Le protocole TCP gère une fenêtre de congestion TCP (TCP Congestion Window) qui définit le nombre de paquets qui peuvent être envoyés avant de recevoir l'acquittement.
Si un paquet d’acquittement est manquant après une période de temps donnée, le paquet sera considéré comme perdu et la fenêtre de congestion sera réduite de moitié (par conséquence le débit sera également réduit de moitié) ; le fenêtre de congestion TCP recommence à augmenter si les paquets d'acquittement sont ensuite reçus correctement.
Partie A : Statistiques à deux variables
Des études expérimentales ont donnés les résultats suivants :
| $t$ : Latence aller-retour (RTT) (en ms) | 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 |
|---|---|---|---|---|---|---|---|---|
| $y$ : Débit TCP avec 2% de perte (en 100 Mbps) | 4.9 | 2.8 | 1.8 | 1.3 | 1.0 | 0.7 | 0.5 | 0.4 |
-
Justifier précisément, grâce à un nombre obtenu sur Geogebra, pourquoi un ajustement affine n'est pas pertinent.
-
On pose $z=\ln\left(\dfrac{20}{y}+10\right)$ et on obtient le tableau suivant :
$t$ : Latence aller-retour (RTT) (en ms) 0 20 40 60 80 100 120 140 $z=\ln\left(\dfrac{20}{y}+10\right)$ 2.645 ... 3.050 3.234 3.401 3.653 3.912 4.094 -
Compléter la valeur manquante.
-
Donner une équation de la droite de régression de $z$ en $t$ , obtenue par la méthode des moindres carrés, sous la forme $z = at + b$, où $a$ et $b$ sont à arrondir à $10^{-2}$.
-
En déduire qu'une expression de $y$ en fonction de $t$, selon cet ajustement, est donné par $y=\dfrac{20}{14e^{0.01t}-10}$, lorsque l'on arrondit à l'entier le plus proche le coefficient multiplicateur devant $e^{0.01t}$.
-
En déduire le débit extrapolé, en Megabits par seconde, pour une latence de 200 millisecondes, si on considère une perte de 2% des paquets.
-
Partie B : Equation différentielle
Votre cheffe considère que la simulation avec 2% de pertes est trop restrictive au vu du type de données
qui sera échangé entre ces centres $A$ et $D$ puisqu'une partie de ces données sera envoyée
suivant le protocole UDP.
En effet, en théorie pour certains protocoles spécifiques comme UDP (où aucun contrôle n'est effectué
à un autre niveau), la vitesse à
laquelle les paquets sont envoyés par l'émetteur n'est pas impactée par le temps nécessaire
pour atteindre l'autre partie, c'est-à-dire par la latence.
Votre cheffe vous demande de considérer que le débit, en Gbps, sera donné par $f(t)$,
où $t$ est la latence en millisecondes.
D'un point de vue théorique, $f$ est solution de l'équation différentielle
$(E) : y'+0.04y=0.32$ avec $y(0)=100$, où $y$ désigne une fonction dérivable sur
$[0 ; +\infty[$ et $y'$ sa fonction dérivée.
-
Déterminer à la main les solutions de l’équation différentielle : $(E_0)$ $y'+0.04y=0$.
-
Déterminer sur Xcas la solution $f$ de l'équation différentielle $(E) : y'+0.04y=0.32$ telle que $f(0)=100$.
-
En utilisant la fonction $f$ obtenue, déduire la latence maximale, en millisecondes, que l'on peut accepter pour avoir un débit minimal de 10 Gbps.
Couple 5
Premier exercice du couple 5
Vous gérez un réseau informatique.
Pour le protéger, vous avez mis en place un VPN, une DMZ et des pare-feux.
Les pares-feux mis en place utilisent diverses techniques pour déterminer
ce qui est autorisé ou refusé à l'accès du réseau, notamment :
-
Filtrage des paquets : empêche ou autorise l'accès sur une base d'adresses IP ou MAC.
-
Filtrage par applications : interdit ou autorise l'accès à des types d'applications spécifiques en fonction des numéros de ports.
-
Filtrage par URL : empêche ou permet l'accès à des sites Web basés sur des URL ou des mots clés spécifiques.
-
Inspection des paquets avec états (Stateful Packet Inspection : SPI) : les paquets entrants doivent être des réponses légitimes aux demandes des hôtes internes. Les paquets non sollicités sont bloqués, sauf s'ils sont expressément autorisés. L'inspection SPI peut éventuellement reconnaître et filtrer des types d'attaques spécifiques telles que le déni de service (DoS).
Comme toute protection, le pare-feu ne protège pas à 100%.
On admet que pour un flux de $x$ données, en Gbps, le pare-feu laisse passer $p(x)$ % des paquets
qu'il aurait dû bloquer avec $p$ une fonction définie sur $[0;+\infty[$ solution de l'équation différentielle
$(E) : 10y'+3y=90$ avec $p(0)=0$, où $y$ désigne une fonction dérivable sur
$[0 ; +\infty[$ et $y'$ sa fonction dérivée.
-
Déterminer à la main les solutions de l’équation différentielle : $(E_0)$ $10y'+3y=0$.
-
Soit $g$ la fonction définie sur $[0;+\infty[$ par $g(t)=C$, où $C$ est une constante réelle.
Déterminer la valeur que doit prendre $C$ pour que $g$ soit une solution de l'équation différentielle $(E)$. -
En déduire la forme de toutes les solutions de l'équation différentielle $(E)$.
-
Pour un flux de 0 Gbps, 0% des paquets reçus auraient dû être bloqués.
Déterminer à la main l'expression de la fonction $p$ donnant le pourcentage de paquets non bloqués qui auraient dû l'être en fonction du flux $x$ arrivant, en Gbps. -
Vérifier, grâce à Xcas, l'expression de la fonction $p$ qui est solution de $(E) : 10y'+3y=90$ telle que $p(0)=0$.
-
On considère la fonction $f$ définie sur $[0;+\infty[$ par $f(x)=30-30\times e^{-0.3x}$.
On admet que $p(x)$ donne le pourcentage de paquets non bloqués qui auraient dû l'être en fonction du flux $x$ arrivant, en Gbps.-
Votre réseau peut accepter de recevoir des données jusqu'à 100 Gbps. Quel est le pourcentage de paquets non bloqués qui auraient dû l'être lorsque le flux est maximal ?
-
Déterminer le pourcentage moyen de paquets non bloqués par erreur lorsque le flux entrant varie entre 1 et 10 Gbps.
-
Second exercice du couple 5
Partie A : Statistiques à deux variables
Devant le pourcentage trop élevé de paquets non bloqués par erreur par le pare-feu mis en place, vous modifier drastiquement les paramétrages de filtrage.
Vous obtenez lors de tests les résultats suivants :
| flux $x$ en Gbps | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pourcentage $y$ de non blocage par erreur | 0 | 0.4 | 0.8 | 1.1 | 1.5 | 1.7 | 2 | 2.2 | 2.4 | 2.6 | 2.8 |
-
Expliquer à l'aide d'un calcul sur Geogebra qu'un ajustement affine de $y$ en $x$ n'est pas pertinent.
-
On pose $z = \ln(5-y)$ et on obtient le tableau suivant, où les valeurs approchées sont arrondies à $10^{-3}$.
Flux $x$ 0 1 2 3 4 5 6 7 8 9 10 $z=\ln(5-y)$ 1.609 1.526 1.435 1.361 1.253 ... 1.099 1.030 0.956 0.875 0.788 -
Compléter la valeur manquante.
-
Donner une équation de la droite de régression de $z$ en $x$, obtenue par la méthode des moindres carrés, sous la forme $z = ax + b$, où $a$ et $b$ sont à arrondir à $10^{-2}$.
-
En déduire une expression de $y$ en fonction de $x$, selon cet ajustement.
-
Lorsque le flux devient très important, vers quel pourcentage tend $y$ ?
Partie B : Suite
Le filtrage par paquet par adresse est telle que désormais si pour toute adresse IP suspecte, la probabilité qu'à le $n$-ième paquet venant de ce site d'être bloqué est donnée par $p_n$, sachant que la suite $(p_n)$ est définie par $p_1=0$ et pour tout entier naturel $n$ non nul $p_{n+1}=0.8p_n+0.2$.
-
Déterminer la probabilité que le troisième paquet venant d'un site suspect soit bloqué.
-
Le but est de déterminer le numéro du paquet venant d'un site suspect tel qu'il est une probabilité supérieur à 0.9 d'être bloqué.
Pour cela, vous devez compléter une des versions suivantes proposant de déterminer le premier entier naturel $n$ tel que $p(n)$ dépasse $0.9$.Version python :
n = ... x = ... # boucle répétitive ...: ... = ... ... = ... print("p(n) dépasse 0.9 à partir du rang n=", ...)Version pseudo-langage :
n ← ... p ← ... ... faire ... ← ... ... ← ... Fin_... Afficher("p(n) dépasse 0.9 à partir du rang n=", ...)Version C++ :
#include <iostream> using namespace std; int main(){ int n = ...; float x = ...; while (...){ ... = ...; ... = ...; } cout<<"p(n) dépasse 0.9 à partir du rang n="<<...<<endl; return 0; } -
On admet que pour tout entier naturel $n$ : $p(n)=1-\left(\dfrac{4}{5}\right)^n$.
Déterminer ce qui va se passer à long terme lorsqu'un site suspect envoie un nombre important de paquets. Justifier.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International