Le cours complet avec les exercices du chapitre est disponible en version imprimable en cliquant ici.
Demander le programme !

Voici une frise historique présentant les premiers mathématiciens qui ont travaillé sur la représentation et l'interprétation géométrique des nombres complexes.

Représentation géométrique.
Affixe d'un point
-
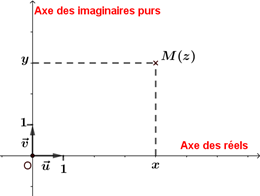
On appelle plan complexe le plan muni d'un repère orthonormé $(0 ; \vec{u},\vec{v})$.
-
À tout nombre complexe $z=x+iy$ avec $x$ et $y$ nombres réels, on associe le point $M$ de coordonnées $(x ; y)$.
-
Réciproquement, à tout point $M(x ; y)$ du plan complexe, on associe le nombre complexe $z=x+iy$.
On dit que le point $M$ est le point image du nombre complexe $z$ et que $z$ est l'affixe du point $M$.
-
Le point $E(-2 ; 3)$ a pour affixe $-2+3i$.
-
Le point image du nombre complexe $1-i$ est le point $F(1 ; -1)$.
Notation et vocabulaire
|
 |
|
 |
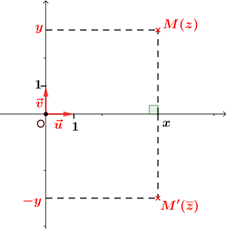
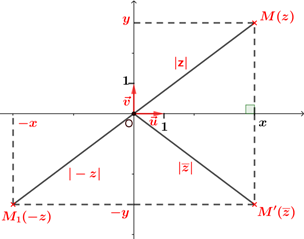
Interprétation géométrique du conjugué
|
Le point $M$ d'affixe $z$ et le point $M'$ d'affixe $\overline{z}$ En effet si $z = x+iy $ $(x\in\mathbb{R} \textrm{ et } y\in\mathbb{R})$, alors $\overline{z}=x-iy$, donc $M$ et $M'$ ont la même abscisse et des ordonnées opposées. |
 |
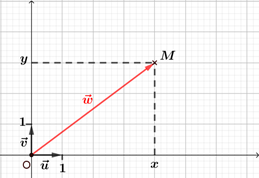
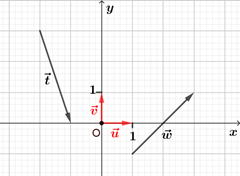
Affixe d'un vecteur
|
Dans le plan complexe, $\vec{w}$ est un vecteur de coordonnées $(x ; y)$. Le point $M$ tel que $\overrightarrow{OM} = \vec{w}$ a pour coordonnées $(x ; y)$, donc le vecteur $\overrightarrow{OM}$ a pour affixe $x+iy$. On dit que le vecteur $\vec{w}$ est le vecteur image du nombre complexe $z$ et que $z$ est l'affixe du vecteur $\vec{w}$. |
 |
|
Soit $M$ un point du plan complexe muni d'un repère d'origine $O$ et $z$ un nombre complexe. Le point $M$ a pour affixe $z$ si, seulement si le vecteur $\overrightarrow{OM}$ a pour affixe $z$. |
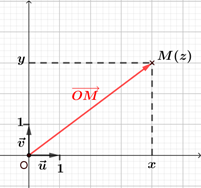 |
-
l'affixe du point $O$ l'origine d'un repère du plan complexe est $0$.
-
l'affixe du vecteur nul $\vec0$ est $0$.
|
 |
Propriétés
En utilisant les propriétés des coordonnées, on déduit les propriétés suivantes
Dans le plan complexe, on considère les vecteurs $\vec{w}$ et $\vec{w'}$ d'affixes respectives $z$ et $z'$ et $k$ un réel.
-
Les vecteurs $\vec{w}$ et $\vec{w'}$ sont égaux si, et seulement si, $z$ = $z'$.
-
Le vecteur $\vec{w}+\vec{w'}$ a pour affixe $z + z'$.
-
Le vecteur $k\vec{w}$ a pour affixe $kz$.
-
L'affixe du vecteur $\overrightarrow{AB}$ est le nombre complexe $z_B-z_A$.
-
L'affixe du milieu $I$ du segment $[AB]$ est le nombre complexe $z_I=\dfrac{z_A+z_B}{2}$.
Soient $A$ et $B$ deux points du plan complexe d'affixes respectives $z_A$ et $z_B$.
Ces 2 propriétés découlent directement des propriétés sur les coordonnées des vecteurs et du milieu d'un segment :
On sait que $\overrightarrow{AB} = \overrightarrow{OB}-\overrightarrow{OA}$, donc $z_\overrightarrow{AB} = z_{\overrightarrow{OB}}-z_{\overrightarrow{OA}}$, Or, $z_\overrightarrow{OA} = z_A$ et $z_\overrightarrow{OB} = z_B$, Ainsi, $z_\overrightarrow{AB} = z_B-z_A$.
Soit $I$ le milieu du segment $[AB]$, alors :
$\overrightarrow{AI} = \overrightarrow{IB}$, donc $z_\overrightarrow{AI} = z_\overrightarrow{IB}$ soit $z_I-z_A = z_B-z_I$, ainsi $2z_I=z_B+z_A$, par conséquent, $z_I=\dfrac{z_A+z_B}{2}$
Dans le plan complexe on donne les points $A$, $B$, $C$ et $D$ d'affixes : $z_A=-3-i$, $z_B=1+i$ $z_C=3-2i$ et $z_D=-1-4i$.
-
Placer les points $A$, $B$, $C$ et $D$ dans le plan complexe en utilisant la figure ci-dessous. Que peut-on dire des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$ ?
-
Déterminer les affixes des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$
-
En déduire la nature du quadrilatère $ABCD$.
Dans le plan complexe on donne les points par leurs affixes $A(1)$, $B(-2 -i)$ et $C(4i)$
-
Déterminer l’affixe du point $D$ tel que $ABCD$ soit un parallélogramme.
-
Déterminer l’affixe du point $M$, centre du parallélogramme $ABCD$.
Dans le plan complexe on donne les points $A$, $B$ et $C$ d'affixes : $z_A=-3+5i$, $z_B=-1+i$ et $z_C=-i$.
-
Placer les points $A$, $B$ et $C$ dans le plan complexe en utilisant la figure ci-dessous et émettre une conjecture.
-
Démontrer ou invalider cette conjecture.
Dans le plan complexe, on note $\mathcal{E}$, l'ensemble des points $M$ d'affixe $z$ tels que $Z=z^2$ soit un réel.
Déterminer l'ensemble $\mathcal{E}$, puis le représenter graphiquement dans un repère orthonormé $(0 ; \vec{u},\vec{v})$.
Module d'un nombre complexe
$(0 ; \vec{u},\vec{v})$ est un repère orthonormé direct du plan complexe.
Définitions et propriétés
|
Soit $M$ le point d'affixe $z$. Le module de $z$, noté $| z |$, est la distance $OM$, c'est-à-dire $| z | = OM$. |
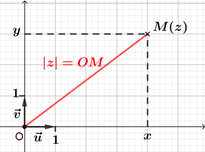 |
|
Pour tout nombre complexe $z$ de forme algébrique $x+iy$ $(x\in\mathbb{R} \textrm{ et } y\in\mathbb{R})$.
|
 |
Soient $z$ un nombre complexe de forme algébrique $x+iy$ $(x\in\mathbb{R} \textrm{ et } y\in\mathbb{R})$ et $M(x ; y)$ son point d'image, alors,
$|z| = OM = \sqrt{(x_M-x_O)^2 + (y_M-y_O)^2}=\sqrt{(x-0)^2 + (y-0)^2}=\sqrt{x^2+y^2}$.
$-z = -x+i(-y)$, donc $|-z| =\sqrt{(-x)^2+(-y)^2}=\sqrt{x^2+y^2}=|z|$
$\overline{z} = x+i(-y)$, donc $|\overline{z}| =\sqrt{x^2+(-y)^2}=\sqrt{x^2+y^2}=|z|$.
$z\overline{z} = (x+iy)(x-iy) = x^2+y^2 =(\sqrt{x^2+y^2})^2=|z|^2 $.
-
Si $x$ est un nombre réel, le module de $x$ est égal à la valeur absolue de $x$.
-
$|z|=0$ équivaut à $z=0$ car $OM=0$ équivaut à $M=O$.
Soient $A$ et $B$ deux points du plan complexe d'affixes respectives $z_A$ et $z_B$.
$AB=|z_B-z_A|$.
Soient $A(x_A ; y_A)$ et $B(x_B ; y_B)$ deux points du plan complexe, alors, $z_A=x_A +iy_A$ et $z_B=x_B +iy_B$.
On sait que $AB = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}$,
et $z_B-z_A=x_B +iy_B-(x_A +iy_A) = (x_B-x_A)+i(y_B-y_A)$, donc, $|z_B-z_A|=\sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}=AB$
-
Dans le plan complexes, placer les points $A(6-3i)$, $B(15+2i)$ et $C(18-3i)$.
-
Que peut-on conjecturer quant à la nature du triangle $ABC$ ?
-
Démontrer ou invalider cette conjecture.
-
Dans le plan complexe, placer les points $D(2-i)$, $E(6-i)$ et $F\left(4+(2\sqrt{3}-1)i\right)$.
-
Montrer que le triangle $DEF$ est équilatéral.
-
Calculer l'aire du triangle $DEF$.
Pour tous nombres complexes $z$, $z'$ et tout nombre entier naturel $n\ge 1$.
-
$|zz'| = |z|\times|z'|$
-
$|z^n| = |z|^n$
-
$\left\lvert\dfrac{1}{z'}\right\rvert = \dfrac{1}{|z'|}$, si $z'\ne0$.
-
$\left\lvert\dfrac{z}{z'}\right\rvert = \dfrac{|z|}{|z'|}$, si $z'\ne0$
-
$|zz'|^2 = zz'\times\overline{zz'}=z\overline{z}\times z'\overline{z'} = |z|^2\times|z'|^2 =(|z||z'|)^2 $. Or, $|zz'|$ et $|z||z'|$ sont deux réels positifs, donc $|zz'|=|z||z'|$.
-
Montrons par récurrence que pour tout entier $n\ge 1$, $|z^n| = |z|^n$ :
-
Pour $n=1$, $|z^1|=|z|=|z|^1$
-
Soit $k \in \mathbb{N}$ avec $k\ge 1$, supposons que $|z^k| = |z|^k$ et montrons que $|z^{k+1}| = |z|^{k+1}$ :
Or, $|z^{k+1}|=|z^k\times z| = |z^k|\times |z| = |z|^k\times |z| = |z|^{k+1}$.
-
Ainsi, pour tout entier $n\ge 1$, $|z^n| = |z|^n$.
-
Soient $z$ et $z'$ deux nombres complexes avec $z'\ne0$ :
Alors, $z'\times\dfrac{1}{z'} = 1$, donc $\left\lvert z'\times\dfrac{1}{z'}\right\rvert = 1$, soit $|z'|\times\left\lvert\dfrac{1}{z'}\right\rvert = 1$, ainsi, $\left\lvert\dfrac{1}{z'}\right\rvert = \dfrac{1}{|z'|}$.
-
Soient $z$ et $z'$ deux nombres complexes avec $z'\ne0$.
Alors, $\left\lvert\dfrac{z}{z'}\right\rvert=\left\lvert z\times\dfrac{1}{z'}\right\rvert = |z|\times\left\lvert\dfrac{1}{z'}\right\rvert = |z|\times\dfrac{1}{|z'|} = \dfrac{|z|}{|z'|}$.
-
Calculer le module de chacun des nombres complexes $\sqrt{3}+i$ et $1-2i$.
-
Déterminer alors le module de chaque nombre complexe :
$z_1=(\sqrt{3}+i)(1-2i)$, $z_2=(\sqrt{3}+i)^3$, $z_3=\dfrac{1}{1-2i}$ et $z_4=\dfrac{\sqrt{3}+i}{1-2i}$.
-
Déterminer les affixes des vecteurs $\overrightarrow{AM}$, et $\overrightarrow{BM}$.
-
Déterminer l'ensemble $\mathscr{E}$ des points $M$ tel que : $|z-2-5i|=|z+3i|$.
On donne les points $A$ et $B$ d'affixes $z_A=2+5i$ et $z_B=-3i$. $M$ désigne un point du plan complexe d'affixe $z$.
-
$M$ est un point d'affixe $z$. Déterminer l'affixe du vecteur $\overrightarrow{AM}$.
-
Déterminer l'ensemble $\mathscr{F}$ des points $M$ d'affixe $z$ du plan dont l'affixe vérifie $|z-1+i|=2$
Le plan complexe est muni d'un repère orthonormé direct $(O;\vec{u},\vec{v})$. On donne le point $A$ d'affixe $1-i$.
Voici un test de quatre questions à faire en autonomie afin de vérifier votre maîtrise du module d'un nombre complexe.
Ensemble $\mathbb{U}$ des nombres complexes de module $1$
|
On note $\mathbb{U}$ l'ensemble des nombres complexes $z$ tels que $|z|=1$. Dans le plan complexe, $\mathbb{U}$ est représenté par le cercle de centre $O$ et de rayon $1$. |
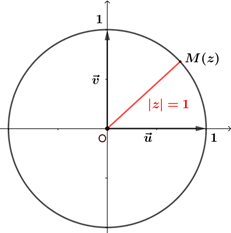 |
Pour tous nombres complexes $z$ et $z'$ de l'ensemble $\mathbb{U}$ :
-
$zz' \in \mathbb{U}$.
-
$\dfrac{1}{z} \in \mathbb{U}$.
-
$|zz'|=|z||z'|$, or $|z|=|z'|=1$, donc $|zz'|= 1$ et $zz'$ appartient à $\mathbb{U}$.
-
$\left\lvert\dfrac{1}{z}\right\rvert = \dfrac{1}{|z|}$, or, $|z|=1$, donc, $\left\lvert\dfrac{1}{z}\right\rvert =1$ et $\dfrac{1}{z} \in \mathbb{U}$.
Soient $z$ et $z'$ deux nombres complexes de l'ensemble $\mathbb{U}$ :
On considère le nombre complexe $j=-\dfrac{1}{2}+i\dfrac{\sqrt3}{2}$.
-
Donner une forme algébrique de $j^2$ et $j^3$.
-
Vérifier que ces nombres complexes appartiennent à $\mathbb{U}$.
-
Calculer $j+j^2+j^3$.
On note $P$, $Q$ et $R$ les points images respectives de $j$, $j^2$ et $j^3$.
Placer ces points dans le plan complexes en utilisant la figure ci-dessous.
Démontrer que le triangle $PQR$ est équilatéral.
Arguments d'un nombre complexe
En cas de besoin de rappels sur le cercle trigonométrique et les valeurs remarquables à connaître, n'hésitez pas à consulter cette page Web de rappel.
$(O ; \vec{u},\vec{v})$ est un repère orthonormé direct du plan complexe.
$\mathscr{C}$ est le cercle trigonométrique de centre $O$.
Définition et interprétation géométrique
|
Soit $z$ un nombre complexe non nul de point image $M$ du plan complexe, $N$ est le point d'intersection du cercle trigonométrique $\mathscr{C}$ et de la demi-droite $[OM)$. On appelle argument de $z$ et on note arg(z) tout nombre $\theta$ dont le point $N$ est l'image sur le cercle trigonométrique $\mathscr{C}$. |
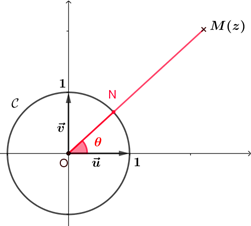 |
-
Un nombre complexe non nul a une infinité d'arguments. Si $\theta$ est un argument d'un nombre complexe $z$, tous les autres sont de la forme $\theta+2k\pi$ avec $k\in \mathbb{Z}$. On note $\theta = arg(z) ~[2\pi]$ et on lit "$\theta$ égal argument de $z$ modulo $2\pi$"
-
L'argument appartenant à $]-\pi ; \pi[$ est appelé argument principal de $z$
Interprétation géométrique
|
On se place dans un plan complexe muni d'un repère orthonormé direct $(O ; \vec{u},\vec{v})$.
|
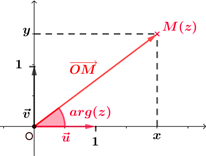 |
Cette propriété est une conséquence directe de la définition.
Le nombre complexe $0$ est le seul nombre complexe qui n'a pas d'argument.
-
Dans le plan complexe, placer les points $A$, $B$, $C$, $D$ d'affixes respectives $1+i$, $-1-i$, $1-i$, $-1+i$.
-
Lire graphiquement un argument de chacun de ces nombres complexes.
Premières propriétés des arguments
|
Pour tout nombre complexe non nul $z$ et tout réel $k$ non nul :
|
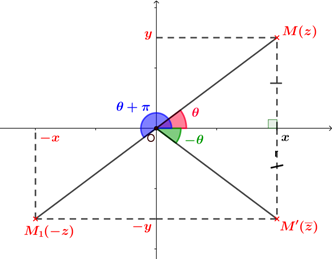 |
Cette propriété est une conséquence directe des propriétés des mesures des angles orientés.
|
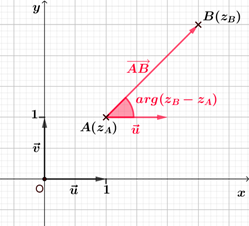 |
|
Soient $A$ et $B$ deux points distincts d'affixes respectives $z_A$ et $z_B$. On note $M$ le point tel que $\overrightarrow{OM}=\overrightarrow{AB}$ et $z_M$ l'affixe de ce point. Alors, $z_M-z_O=z_B-z_A$, soit $z_M=z_B-z_A$. De plus, $\left(\vec{u} ; \overrightarrow{OM}\right)=arg(z_M) ~[2\pi]$ soit, $\left(\vec{u} ; \overrightarrow{OM}\right)=arg(z_B-z_A) ~[2\pi]$. Or, $\left(\vec{u} ; \overrightarrow{OM}\right)=\left(\vec{u} ; \overrightarrow{AB}\right)$, donc $\left(\vec{u} ; \overrightarrow{AB}\right)=arg(z_B-z_A) ~[2\pi]$. |
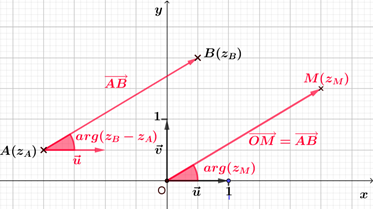 |
Soit $z$ un nombre complexe non nul de forme algébrique $x+iy$ ($x$ et $y$ réels).
-
Alors un argument de $z$ est un réel $\theta$ tel que $\left\{ \begin{array}{l!l} cos(\theta)=&\dfrac{x}{|z|}\\[3pt] sin(\theta)=&\dfrac{y}{|z|} \end{array}\right.$
|
Soit $z=x+iy$ ($x\in\mathbb{R}$ et $y\in\mathbb{R}$) un nombre complexe non nul dont un argument est $\theta$. $M$ est le point image de $z$ et $N$ est le point d'intersection du cercle trigonométrique $\mathcal{C}$ et la demi-droite $[OM)$. Donc, le point $N$ a pour coordonnées $(cos(\theta) ; sin(\theta))$. Ainsi, l'affixe du point $N$ est $z_N=cos(\theta)+isin(\theta)$. Or, $|z|=OM$ et $\overrightarrow{ON}=\dfrac{1}{OM}\overrightarrow{OM}=\dfrac{1}{|z|}\overrightarrow{OM}$, donc $\overrightarrow{OM}=|z|\overrightarrow{ON}$, ainsi $z=|z|(cos(\theta)+isin(\theta))$, d'où, $x+iy = |z|cos(\theta)+i|z|sin(\theta)$, ainsi, $x=|z|cos(\theta)$, soit $cos(\theta)=\dfrac{x}{|z|}$ et $y=|z|sin(\theta)$, soit $sin(\theta)=\dfrac{y}{|z|}$. |
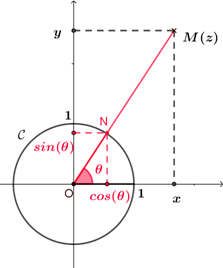 |
-
Dans le plan complexe, placer les points $A$ et $B$ d'affixes respectives $3+3i$ et $-2+2i$.
-
Déterminer un argument de l'affixe de $A$, puis de $B$.
-
En déduire la mesure de l'angle $\widehat{AOB}$ et la nature du triangle $AOB$.
$A$ et $B$ sont les points du plan complexes : $z_A=-2\sqrt{3}+2i$ et $z_B=\overline{z_A}$.
-
Déterminer un argument de l'affixe de chacun des points $A$ et $B$.
-
En déduire la mesure de l'angle $\widehat{AOB}$.
-
Démontrer que le triangle $AOB$ est équilatéral.
-
-
Déterminer un argument du nombre complexe $z=-1+i\sqrt3$.
-
Soit $z_1$ un nombre complexe tel que $|z_1|=3$ et $arg(z_1)=\dfrac{3\pi}{2} ~[2\pi]$. Déterminer la forme algébrique du nombre complexe $z_1$.
-
-
-
Déterminer un argument du nombre complexe $z_2=1+i$. On note $M_2$ le point d'affixe $z_2$.
-
Déterminer dans le repère orthonormé $(O ; \vec{u},\vec{v})$, l'ensemble des points $M$ d'affixe $z$ tels que $arg(z)= \dfrac{\pi}{4} ~[2\pi]$
Le plan complexe est muni d'un repère orthonormé direct $(O ; \vec{u},\vec{v})$.
-
Forme trigonométrique d'un nombre complexe
$z$ est un nombre complexe non nul.
L'écriture $z=|z|(cos(\theta)+isin(\theta))$ où $arg(z)=\theta ~[2\pi]$ est appelée une forme trigonométrique de $z$.
-
Deux nombres complexes non nuls sont égaux si, et seulement si, ils ont le même module et même argument à un multiple de $2\pi$ près.
-
Si $z=r(cos(\theta)+isin(\theta))$ avec $r$ un réel strictement positif alors $|z|=r$ et $arg(z)=\theta$ $~[2\pi]$.
-
Déterminer le module et un argument de chaque nombre complexe puis l'écrire sous forme trigonométrique.
a.$z_1=\dfrac{2}{5}i$. b.$z_2=1+i\sqrt{3}$. c.$z_3=-4i$. d.$z_4=-10$. e.$z_5=2-2i\sqrt{3}$. f.$z_6=-1+i$.
-
En déduire, sans calculs supplémentaires, une forme trigonométrique de $\overline{z_6}$ et $\sqrt{2}z_6$.
Dans chaque cas, écrire sous forme algébrique le nombre complexe $z$.
-
$z=2\left(\cos\left(\dfrac{\pi}{4}\right)+i\sin\left(\dfrac{\pi}{4}\right)\right)$.
-
$z=\sqrt{3}\left(\cos\left(\dfrac{\pi}{3}\right)+i\sin\left(\dfrac{\pi}{3}\right)\right)$.
-
$z=\sqrt{3}\left(\cos\left(-\dfrac{\pi}{6}\right)+i\sin\left(-\dfrac{\pi}{6}\right)\right)$.
-
$z=8\left(\cos\left(\dfrac{3\pi}{4}\right)+i\sin\left(\dfrac{3\pi}{4}\right)\right)$.
$z$ est un nombre complexe non nul de forme algébrique $z=x+iy$ avec $x\in \mathbb{R}$ et $y\in \mathbb{R}$ et dont une forme trigonométrique est $z=r(\cos(\theta)+isin(\theta))$ avec $z=a+ib$ avec $r$ et $\theta$ des réels et $r>0$.
Voici une fonction FT qui :
-
prend en paramètres deux nombres réels
aetbqui correspondent respectivement aux parties réelle et imaginaire d'un nombre complexe $z$, -
renvoie le triplet
r,c,scorrespondant respectivement au module de $z$, à $\cos(\theta)$ et à $\sin(\theta)$.
from math import *
def FT(a, b):
r = ..................
c = ..................
s = .................
return r, c, s
-
Compléter les lignes 3, 4 et 5 de ce programme
-
Saisir et tester cette fonction.
En cas de difficulté avec votre environnement de développement, vous pouvez travailler en ligne sur trinket avec ce lien.
Voici un test de trois questions à faire en autonomie afin de vérifier votre maîtrise sur l'argument et la forme trigonométrique d'un nombre complexe.
Exercices
Module et arguments d'un nombre complexes
-
Placer les points $A$, $B$, $C$, $D$ d'affixes respectives $-4-3i$, $3-2i$, $4+5i$, $-3+4i$.
-
Quelle est la nature du quadrilatère $ABCD$ ?
On donne dans le plan complexe les points $A$, $B$ et $C$ d'affixes respectives : $$z_A=-2 \textrm{, } z_B=1+i \textrm{ et } z_C=-1-3i.$$
-
Placer les points $A$, $B$ et $C$ dans le plan complexe.
-
Quelle est la nature du triangle $ABC$ ? Justifier.
Dans chaque cas, déterminer l'ensemble des points $M$ d'affixe $z$ tels que :
-
$|z-3|=2$.
$|z+2i|=1$.
$|z-i|=|z+2|$.
$|z-2+i|=|z|$.
On considère les nombres complexes : $a=1+i\sqrt{3}$ et $b=\sqrt{3}-i$.
On note $A$ et $B$ les points d'affixes $a$ et $b$.
-
-
Donner une forme trigonométrique du nombre complexe $a$, puis de $b$.
-
Placer précisément les points $A$ et $B$ dans le plan complexe.
-
Démontrer que le triangle OAB est rectangle isocèle en $O$.
-
-
$K$ est le milieu du segment $[AB]$.
-
Placer le point $K$.
-
Calculer son affixe.
-
-
On considère le nombre complexe $c=1+\sqrt{3}+i(\sqrt{3}-1)$.
On note $C$ le point d'affixe $c$.
-
Montrer que $K$ est le milieu de $[OC]$.
-
Placer le point $C$ et montrer que le quadrilatère $OACB$ est un carré.
-
On considère la suite des nombres complexes $\left(z_n\right)$ définie pour tout entier naturel $n$ par \[z_n = \dfrac{1 + \text{i}}{(1-\text{i})^n}.\]
On se place dans le plan complexe d'origine $O$.
-
Pour tout entier naturel $n$, on note $A_n$ le point d'affixe $z_n$.
-
Démontrer que, pour tout entier naturel $n$, $\dfrac{z_{n+4}}{z_n}$ est réel.
-
-
Démontrer alors que, pour tout entier naturel $n$, les points $O$, $A_n$ et $A_{n+4}$ sont alignés.
-
Montrer que pour tout entier naturel $n$, $z_n = \dfrac{(1 + \text{i})^{n+1}}{2^n}.$
En déduire pour quelles valeurs de $n$ les points $A_n$ appartiennent-ils à l'axe des abscisses ?
Dans tout l'exercice, le plan est rapporté au repère orthonormé direct $\left(O\ ;\ \overrightarrow{u}, \overrightarrow{v}\right)$.
On donne les points $A$ et $B$ d'affixes $z_A=1+i\sqrt{3}$ et $z_B=2i$.
-
-
Donner une forme trigonométrique de $z_A$ et $z_B$.
-
Placer avec précision ces points sur une figure.
-
-
$F$ est le point d'affixe $z_F=z_A+z_B$.
-
Placer sur la figure le point $F$.
-
Donner la forme algébrique de $z_F$.
-
Démontrer que $OAFB$ est un losange.
-
-
$U$ est le point d'affixe 1 dans le repère orthonormé direct $\left(O\ ;\ \overrightarrow{u}, \overrightarrow{v}\right)$.
-
Justifier que $\widehat{UOF}=\dfrac{5\pi}{12}$ et écrire une forme trigonométrique de $z_F$.
-
Démontrer alors que : $\cos\left(\dfrac{5\pi}{12}\right)=\dfrac{\sqrt{6}-\sqrt{2}}{4}$ et $\sin\left(\dfrac{5\pi}{12}\right)=\dfrac{\sqrt{6}+\sqrt{2}}{4}$.
-
$A$ et $B$ sont les points d'affixes respectives : $z_A=1$ et $z_B=5$
$\Delta$ est la médiatrice du segment $[AB]$
A tout point $M$ d'affixe $z$, différent de $A$, on associe le point $M'$ d'affixe $z'$ telle que : $z'=\dfrac{2z-10}{z-1}$.
On se propose de déterminer l'ensemble $\mathscr{E}$ des points $M'$ lorsque $M$ parcourt $\Delta$.
-
Conjecture avec un logiciel de géométrie
-
Placer les points $A$ et $B$ en saisissant par exemple :
-
Créer la médiatrice $\Delta$ du segment $[AB]$ et placer un point $M$ sur $\Delta$.
-
Placer le point $M'$ en saisissant :

-
Afficher la trace de $M'$ et déplacer le point $M$ afin de conjecturer la nature de l'ensemble $\mathscr{E}$.
-
-
Démonstration
-
Justifier que $|z-5|=|z-1|$ et en déduire que $|z'|=2$.
-
Que peut-on dire alors du point $M'$ et de l'ensemble $\mathscr{E}$ ?
-
F est un point d'affixe $f$ avec $|f|=2$ et $f\neq 2$.
Démontrer qu'il existe un point $K$ d'affixe $k$, de la droite $\Delta$ tel que : $f=\dfrac{2k-10}{k-1}$.
-
Déterminer alors l'ensemble $\mathscr{E}$.
$M$ d'affixe est un point quelconque de $\Delta$.
À tout nombre complexe $z$, différent de $-i$, on associe le nombre complexe $z'$ défini par : $z'=\dfrac{1+iz}{1-iz}$.
On note $M$ le point d'affixe $z$, et $M'$ le point d'affixe $z'$
On se propose de déterminer l'ensemble des nombres complexes $z'$ lorsque $z$ est un réel.
-
Donner la forme algébrique de $z'$ dans chacun des cas suivants :
-
$z=3$
-
$z=-4$
-
$z=i$
-
$z=1+i$
-
-
Conjecture avec un logiciel de géométrie
-
Sur la figure ci-dessous, nous avons place un point $M$ d'affixe $z$, sur l'axe des abscisses.
Saisissez :
-
Déplacer la point $M$ afin de conjecturer la nature de l'ensemble des nombres complexes $z'$.
-
-
Démontrer que si $z$ est un nombre réel, alors $z'$ appartient à l'ensemble $\mathbb{U}$ des nombres complexes de module 1.
-
La réciproque de l'implication précédente est-elle vraie ? Le démontrer.
-
Déterminer les points $M$ d'affixe non nulle $z$ du plan complexe tels que $z$, $\dfrac{1}{z}$ et $1+z$ aient le même module.
-
Écrire en fonction de $z$ les normes des vecteurs $\overrightarrow{AM}$, $\overrightarrow{BM}$ et $\overrightarrow{CM}$.
-
Déterminer l'ensemble $\mathscr{E}$ des points $M$ tel que : $|z-1|=|z-i|$ et $|z-3-2i|\leq 2$.
$A$, $B$ et $C$ sont les points d'affixes $z_A=1$, $z_B=i$ et $z_C=3+2i$. $M$ désigne un point du plan complexe d'affixe $z$.
Le plan complexe est muni d'un repère orthonormé direct $(O;\vec{u},\vec{v})$.
A tout point $M$ d'affixe $z$ non nulle, on associe le point $M'$ d'affixe $z'$ telle que : $z'=-\dfrac{1}{\overline{z}}$.
On se propose de déterminer l'ensemble $\mathscr{E}$ des points $M'$ lorsque $M$ parcourt $\Delta$.
-
-
Montrer que $z'=-\dfrac{z}{|z|^2}$.
-
En déduire que les points $O, M, M'$ sont alignés.
-
-
Démontrer que $\overline{z'+1}=\dfrac{1}{z}(z-1)$.
-
On nomme $A$ et $B$ les points d'affixes respectivement $1$ et $-1$.
On désigne par $\Gamma$ le cercle de centre $A$ contenant le point $O$. $\Gamma^*$ désigne le cercle $\Gamma$ privé du point $O$.
On suppose dans cette question que le point $M$ appartient à $\Gamma^*$.
-
Justifier l'égalité $|z-1|=1$.
Démontrer que $|z'+1|=|z'|$. Interpréter géométriquement cette égalité.
-
Déduire de ce qui précède une construction géométrique du point $M'$ à partir du point $M$.
-
-
On désigne par $\mathscr{C}$ le cercle de diamètre $[AB]$. On suppose dans cette question que le point $M$ appartient à $\mathscr{C}$.
Démontrer que $M'$ appartient à $\mathscr{C}$ et construire $M'$.
On définit, pour tout entier naturel $n$, les nombres complexes $z_n$ par : on considère la suite $(z_n)$ définie par :
\[\left\{\begin{array}{l c l} z_{0}&=& 16\\ z_{n+1}&=&\dfrac{1 + \text{i}}{2}z_{n},\: \text{pour tout entier naturel} \: n. \end{array}\right.\]On note $r_{n}$ le module du nombre complexe $z_{n}\: : r_{n} =\left|z_{n}\right|$.
Dans le plan muni d'un repère orthonormé direct d'origine O, on considère les points $A_{n}$ d'affixes $z_{n}$.
-
-
Calculer $z_{1}, z_{2}$ et $z_{3}$.
-
Placer les points $A_{1}$ et $A_{2}$ sur le graphique ci-dessous (ou sur une feuille).
-
Écrire le nombre complexe $\dfrac{1 + \text{i}}{2}$ sous forme trigonométrique.
-
Démontrer que le triangle $OA_{0}A_{1}$ est isocèle rectangle en $A_{1}$.
-
-
-
Démontrer que la suite $\left(r_{n}\right)$ est géométrique, de raison $\dfrac{\sqrt{2}}{2}$.
-
La suite $\left(r_{n}\right)$ est-elle convergente ?
-
Interpréter géométriquement le résultat précédent.
-
-
-
Démontrer que pour tout entier naturel $n \::\: A_{n}A_{n+1} = r_{n+1}$.
-
Donner une expression de $L_{n}$ en fonction de $n$.
-
Déterminer la limite éventuelle de la suite $\left(L_{n}\right)$.
On note $L_{n}$ la longueur de la ligne brisée qui relie le point $A_{0}$ au point $A_{n}$ en passant successivement par les points $A_{1}, A_{2}, A_{3}$, etc.
Ainsi $L_{n} = \displaystyle\sum_{i=0}^{n-1} A_{i}A_{i+1} = A_{0}A_{1} + A_{1}A_{2} + \ldots + A_{n-1}A_{n}.$
-
-
Le but est désormais d'obtenir l'ensemble des indices $n$ tels que $z_n$ soit un nombre imaginaire pur.
-
Compléter le script suivant de sorte que la fonction
suite_zrenvoie l'expression de $z_n$ dans le cas où l'entier $n$ est saisi comme argument.def suite_z(n): z = ... for ... z = ... return zcomplexe(2,3)permet en langue Python de travailler avec le nombre complexe $2+3i$. -
Compléter le script suivant de sorte que
solutions(n)renvoie la liste de tous les nombres entiers naturels $m$ compris entre 0 et $n$ tels que $z_m$ soit un imaginaire pur.def solutions(n): lst = [] ... if suite_z(...)... ... return lst -
En s'aidant du script précédent que pouvez-vous conjecturer quant à l'ensemble des nombres entiers $n$ tels que $z_n$ soit un nombre complexe imaginaire pur ?
-
Démontrer la conjecture émise quant à l'ensemble précédemment conjecturé.
-
Synthèses
$(0 ; \vec{u},\vec{v})$ est un repère orthonormé direct du plan complexes.
Pour la figure, on pendra pour unité 5 cm.
On considère la suite $(z_n)$ définie par $\left\{ \begin{array}{l} z_0=0\\ z_{n+1}=\dfrac{1}{2}(1+i) z_n-1+i \textrm{, pour tout } n\in\mathbb{N} \end{array} \right.$
Pour tout entier naturel $n$, on note $M_n$ le point du plan complexe qui a pour affixe $z_n$.
On considère le point $A$ d'affixe $z_A=-2$.
-
-
Déterminer la forme algébrique de $z_1$ , $z_2$, $z_3$ et $z_4$.
-
Placer, dans le plan complexe, les points $M_0$, $M_1$ , $M_2$, $M_3$ et $M_4$.
-
-
Voici une fonction Suite_1 écrite dans le langage Python.
-
Saisir cette fonction et l'exécuter pour $n=1$, $n=2$, $n=3$ et $n=4$. Quels résultats retrouve-t-on ainsi ?
-
Utiliser cette fonction pour obtenir $z_5$ , $z_6$, $z_7$ et $z_8$.
-
Placer, dans le plan complexe, les points $M_5$, $M_6$ , $M_7$ et $M_8$.
-
$(Z_n)$ est la suite définie sur $\mathbb{N}$ par $Z_n=z_n+2$.
-
Quel est le vecteur dont l'affixe est $Z_n$ ?
-
Montrer que pour tout $n\in\mathbb{N}$, $Z_{n+1}=\dfrac{1}{2}(1+i)Z_n$.
-
Déterminer $Z_0$.
-
Écrire en langage Python, une fonction Suite_2 qui, pour une valeur $n$ du paramètre renvoie le nombre complexe $Z_n$.
-
Saisir ce programme à l'aide de cette fonction, conjecturer une propriété des nombres $Z_{4k}$ et $Z_{4k+2}$, pour $k$ nombre entier naturel.
-
-
Démontrer que pour tout entier naturel $n$, $Z_n=\dfrac{(1+i)^n}{2^{n-1}}$. En déduire l'expression de $z_n$ en fonction de $n$.
-
Démontrer que pour tout entier naturel $k$, $(1+i)^{4k}$ est un nombre réel et $(1+i)^{4k+2}$ est un imaginaire pur. Que peut-on en déduire pour les points $M_{4k}$ et $M_{4k+2}$ ?
-
def Suite_1(n):
z = 0
for i in range(1, n+1):
z = complex(1, 1)/2*z - 1 + complex(0, 1)
return z complex(x, y)permet d'obtenir en Python le nombre complexe $x+iy$. Les complexes se notent :
1+1j, 3j, -1+0j, ...
En cas de difficulté avec votre environnement de développement, vous pouvez travailler en ligne sur trinket avec ce lien.
Écrire l'expression de $Z_{n+1}$ et mettre $1+i$ en facteur.
Exécuter ce programme pour des paramètres de la forme $4k$ et $4k+2$.
En cas de difficulté avec votre environnement de développement, vous pouvez travailler en ligne sur trinket avec ce lien.
-
Démontrer que pour tout entier naturel $n$, $|Z_n|=2\times\left(\dfrac{\sqrt{2}}{2}\right)^n$.
-
Quelle est la limite de la suite $(|Z_n|)$ lorsque $n$ tend vers $+\infty$.
-
Interpréter géométriquement ce résultat.
On considère $(a_n)$ la suite définie pour tout entier naturel $n$ par $a_n=arg(Z_n)=arg(z_n+2)$.
-
On admet les deux propriétés suivantes sur les arguments qui seront démontrées lors du chapitre C3 :
-
Pour tout entier naturel $n$ et tout nombre complexe non nul $z$ : $arg(z^n)=n\times arg(z)~ [2\pi]$.
-
Pour tout nombre complexe non nul $z$ et $z'$ : $arg\left(\dfrac{z}{z'}\right)=arg(z)-arg(z')~ [2\pi]$.
Démontrer que $(a_n)$ est une suite arithmétique dont le premier terme et la raison sont à déterminer.
-
-
Démontrer que pour tout entier naturel $n$, les points $A$, $M_n$ et $M_{n+4}$ sont alignés.
La suite des points $M_n$ forment une spirale lorsque l'on relie deux points successifs deux à deux.
-
Sur la figure construite à la question 1.b., tracer les premiers segments de la spirale $M_0M_1$, $M_1M_2$, $M_2M_3$, ... afin de visualiser la spirale.
-
Démontrer que pour tout entier naturel $n$ $M_{n+1}M_n=|Z_{n+1}|$.
-
On note $L_{n}$ la longueur de la ligne brisée qui relie le point $M_{0}$ au point $M_{n}$ en passant successivement par les points $M_{1}, M_{2}, M_{3}$, etc.
Ainsi, $L_{n} = \displaystyle\sum_{i=0}^{n-1} M_{i}M_{i+1} = M_{0}M_{1} + M_{1}M_{2} + \ldots + M_{n-1}M_{n}.$Déterminer une expression simplifiée de $L_n$ en fonction de $n$.
-
Déterminer la limite de la suite $(L_n)$ lorsque $n$ tend vers $+\infty$.
Interpréter géométriquement cette limite au niveau de la spirale. -
Soit $n$ un entier naturel.
Interpréter géométriquement $a_n=arg(z_n+2)$ en utilisant les points $O$, $A$ et $M_n$. -
Déterminer la limite de la suite $(a_n)$ lorsque $n$ tend vers l'infini.
Qu'en déduire quant à la spirale formée par l'ensemble des points $M_n$ ?
Le plan complexe est muni d'un repère orthonormé direct.
-
Résultats préliminaires
$Z$ désigne u nombre complexe.
-
Démontrer que $Re(Z)\leqslant |Z|$.
-
Démontrer que $Re(Z)=|Z|$ si, seulement si, $Z$ est un nombre réel positif.
-
- Inégalité triangulaire pour deux nombres complexes
$z$ et $z'$ désignes deux nombres complexes.
-
À partir de l'égalité $|z+z'|^2=(z+z')(\overline{z+z'})$, démontrer que :
$|z+z'|^2=|z|^2+2Re\left(z+\overline{z'}\right)+|z'|^2$ -
À l'aide de l'inégalité de la question 1.a., démontrer que : $|z+z'|^2\leqslant|z|^2+2|z|z'|+|z'|^2$
-
En déduire alors l'inégalité triangulaire : $|z+z'|\leqslant|z|+|z'|$.
-
À l'aide de 1.b., démontrer que $|z+z'|\leqslant|z|+|z'|$ si, seulement si, $z\overline{z'}$ est un nombre réel positif.
-
-
Etude géométrique du cas d'égalité
On donne la forme algébrique des nombres complexes $z$ et $z'$ :
$z=x+iy$ et $z'=x'+iy'$ avec $x$, $y$, $x'$, $y'$ nombres réels.
-
Exprimer $z\overline{z'}$ en fonction de $x$, $y$, $x'$ et $y'$.
-
Montrer que $z\overline{z'}$ est un nombre réel positif si, et seulement si,
\[\text{ (1) }\left\{\begin{array}{l c l} xy'-x'y&=&0\\ xx'+yy'&\geqslant&0\\ \end{array}\right.\] -
Dans le plan complexe, on note $\vec{u}$ et $\vec{v}$ les vecteurs d'affixes respectives $z$ et $z'$.
Traduire le système (1) à l'aide du déterminant du couple $(\vec{u} ; \vec{v})$ et du produit scalaire $\vec{u}.\vec{v}$.
-
En déduire que $z\overline{z'}$ est un nombre réel positif si, seulement si, les vecteurs $\vec{u}$ et $\vec{v}$ sont colinéaires et de même sens.
-
-
Une conséquence de l'inégalité triangulaire
-
Démontrer que $|z|\leqslant|z-z'|+|z'|$ et en déduire que $|z|-|z'|\leqslant|z-z'|$.
-
Démontrer que : $|z'|-|z|\leqslant|z-z'|$.
-
En déduire un encadrement de $|z|-|z'|$.
-
Justifier alors l'inégalité $\lvert|z|-|z'|\rvert\leqslant|z-z'|$.
$z$ et $z'$ désignent deux nombres complexes.
Le but de cet exercice est de commencer à plonger dans le monde fascinant de l'ensemble de Mandelbrot.

Par Simpsons contributor sur Wikipédia anglais —
Transféré de en.wikipedia à Commons par Franklin.vp
utilisant CommonsHelper., Domaine public, Lien
Soit $c$ un nombre complexe. On considère la suite de nombres complexes $(z_n)$ définie par $z_0=0$
et pour
tout entier naturel $n$ $z_{n+1}=z_n^2+c$.
Pour tout entier naturel $n$, on pose $u_n=|z_n|$.
L'ensemble de Mandelbrot, noté $\mathcal{M}$, est l'ensemble des nombres
complexes
$c$ tel que le suite $(u_n)$ reste bornée.
-
On note, pour tout entier naturel $n$, $z_n=x_n+i y_n$ et $c=a+ib$, pù $a$, $b$, $x_n$ et $y_n$ sont des nombres réels.
-
Justifier que, pour tout entier naturel $n$, $x_{n+1}=x_n^2-y_n^2+a$.
-
Exprimer $y_{n+1}$ en fonction de $x_n$, $y_n$ et $b$.
-
-
Il a été prouvé que, dès qu'il existe un terme de la suite $(u_n)$ strictement supérieur à 2, alors la suite $(u_n)$ n'est pas bornée.
Le but est d'utiliser cette propriété afin d'obtenir une fonction
est_dans_Mandelbrot:-
qui prend comme argument les réels $a$ et $b$ définissant le nombre complexe $c$,
-
qui calcule les 100 premiers termes de la suite $(z_n)$ tant que le module $u_n$ reste inférieur ou égal à 2
-
qui ne renvoie rien mais affiche soit "NON" si le module $u_n$ a dépassé 2 sur les 100 premiers termes, soit "possible" sinon.
-
Proposer une telle fonction écrite en langage Python
Si vous ne vous sentez pas très à l'aise en programmation, vous pouvez télécharger ici un programme à compléter.
-
Tester cette fonction avec $c=0$ $c=0.6+0.6i$, $c=0.3+0.3i$, $c=0.6+0.6i$, $c=-1+0.2i$, $c=-0.6+0.4i$ et $c=-0.8+0.3i$.
-
D'après-vous, est-ce que si $A$ et $B$ sont deux points du plan complexe tels que leur affixe appartienne à l'ensemble de Mandelbrot alors leur milieu a une affixe qui appartient aussi à cet ensemble de Mandelbrot ?
-
-
-
Modifier la fonction précédente
est_dans_Mandelbrotde sorte qu'elle renvoieTrueau lieu de l'affichage "possible" etFalseau lieu de l'affichage "NON" -
Intégrer la fonction modifiée dans le script ci-dessous qui est aussi à compléter.
from math import sqrt import matplotlib.pyplot as plt # bibliothèque permettant d'obtenir une représentation graphique def est_dans_mandelbrot(a, b): ... liste_x = [] # liste des abscisses des points trouvés comme appartenant à l'ensemble de Mandelbrot liste_y = [] # liste des ordonnées des points trouvés comme appartenant à l'ensemble de Mandelbrot for i in range(401): for j in range(401): if est_dans_mandelbrot(-2+i/100, -2+j/100): ... ... plt.axis([-2, 2, -2, 2]) # limitation de la fenêtre de vision plt.xlabel('partie réelle') # étiquette sur l'axe des abscisses plt.ylabel('partie imaginaire') # étiquette sur l'axe des ordonnées plt.title('ensemble de Mandelbrot') # titre plt.axis('equal') # Pour avoir un repère orthonormé plt.grid() # affichage d'une grille plt.scatter(liste_x, liste_y) # affichage des points trouvés comme appartenant à l'ensemble de Mandelbrot plt.show() # réalisation du visuel dans une fenêtre graphique extérieure -
Exécuter le programme et observer le résultat obtenu.
Le but ici est d'obtenir une première représentation de cet ensemble de Mandelbrot.
Pour cela, on examine chaque point du carré dont les deux coordonnées sont comprises entre -2 et 2 et sont du type $-2 + i/100$ avec $i$ variant entre 0 et 400. On dessine ce point s'il est l'image d'un nombre complexe appartenant à l'ensemble de Mandelbrot.
Cet ensemble a été étudié depuis le début du $XX^e$ siècle par les mathématiciens français Fatou et Julia.
Cet ensemble s'appelle l'ensemble de Mandelbrot car Benoît Mandelbrot, un mathématicien américain d'origine polonaise et française a obtenu une représentation de cet ensemble grâce à un ordinateur en 1980.
Cependant, la plus ancienne représentation obtenue de cet ensemble le fut en 1978 par Brooks et Matelski. La voici :
-
Savoirs et savoirs-faire
-
la notion d'image et d'affixe,
-
la notion du module d'un nombre complexe,
-
la notion d'argument d'un nombre complexe non nul,
-
interpréter géométriquement le module d'un nombre complexe,
-
interpréter géométriquement un argument d'un nombre complexe non nul,
-
refaire la démonstration de la formule $z^2=z\overline{z}$,
-
refaire la démonstration du module d'un produit,
-
refaire la démonstration du module d'une puissance,
-
déterminer et utiliser des affixes,
-
calculer et utiliser le module d'un nombre complexe,
-
déterminer et utiliser un argument d'un nombre complexe non nul,
-
utiliser les propriétés sur le module d'un nombre complexe,
-
utiliser les propriétés sur le module d'un nombre complexe,
-
déterminer rigoureusement la nature d'un triangle ou d'un quadrilatère,
-
passer d'un forme algébrique à une forme trigonométrique,
-
passer d'un forme trigonométrique à une forme algébrique.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International
