La loi de Poisson porte le nom d'un mathéticien français du XIXème siècle. Cette loi de Poisson est utilisée dans différents domaines :
-
l'étude d'événements rares (accidents, ...),
-
l'estimation de temps d'attente,
-
l'estimation du nombre de communications dans un temps donné,
-
l'étude d'un défaut de crédit en finance, ...
Introduction
Cette loi de Poisson est en lien avec la
loi exponentielle déjà vue.
Voici un problème concret en lien avec votre domaine de compétences et d'intérêt :
On s'intéresse à la modélisation du trafic internet au terminal informatique d'une grande société.
On admet que la variable aléatoire $T$ correspondant au temps, en secondes, séparant l'arrivée de deux paquets de données
à ce terminal suit la loi exponentielle de paramètre $\lambda=700$ et que les arrivées des paquets sont indépendantes
les unes des autres.
On considère la variable aléatoire $X$ qui à toute durée de 0.01 seconde, fait correspondre le nombre de paquets de données
arrivant à ce terminal.
On souhaite étudier la loi de la variable aléatoire $X$.
Voici un programme écrit en pseudo-langage en lien avec cette modélisation du trafic arrivant à un terminal informatique :
x prend la valeur entière -1 s prend la valeur 0 Tant que s≤0.01 faire s prend la valeur s-ln(random())/700 x prend la valeur x+1 Fin Tant que Afficher x
On admet que la loi exponentielle de paramètre $\lambda=700$ est simulée par l'instruction -ln(random())/700
où random() est un générateur de nombre aléatoire entre 0 et 1.
-
Quel est le signe de
ln(random())/700? -
L'algorithme peut-t-il afficher -1 ? Si oui à quelle condition ?
-
L'algorithme peut-t-il afficher 0 ? Si oui à quelle condition ?
-
L'algorithme peut-t-il afficher 1 ? Si oui à quelle condition ?
-
Combien de fois la boucle
Tant quedoit-elle être exécutée pour que l'algorithme affiche la valeur 2 ? -
Interpréter le sens des variables
xetsde cet algorithme dans le contexte de la simulation du trafic arrrivant à un terminal informatique.
-
Programmer l'algorithme précédent en langage C++ ou télécharger et lancer directement sur Xcas ce fichier qui contient le programme précédent écrit dans un langage exécutable directement sur Xcas.
Pour l'exécuter sur Xcas, il suffit d'appuyerant sur la touche OK. -
Lancer plusieurs fois le programme précédent afin de recopier et compléter le tableau suivant en notant le nombre de paquets de données simulés arrivant au terminal durant un centième de seconde :
Exécution numéro 1 2 3 4 5 6 7 8 9 10 Nombre de paquets -
Estimer le nombre moyen de paquets arrivant durant 0.01 seconde lorsque le paramètre est $\lambda=700$.
-
Reproduire et compléter la phrase conclusive suivante :
En moyenne, il semble qu'il y a en moyenne environ ... paquets arrivant sur le terminal en 0.01 seconde.
On désire effectuer 10000 simulations de la variable $X$ puis de représenter la variable $X$ en obtenant l'histogramme donnant la probabilité en fonction du nombre de paquets arrivés.
-
Modifier le programme précédent en C++ afin d'obtenir une telle simiulation ainsi que l'histogramme voulu ou plus simplement télécharger et exécuter sur Xcas ce fichier en appuyant sur la touche OK.
-
Voici deux représentations graphiques obtenues en lançant deux fois ce programme :
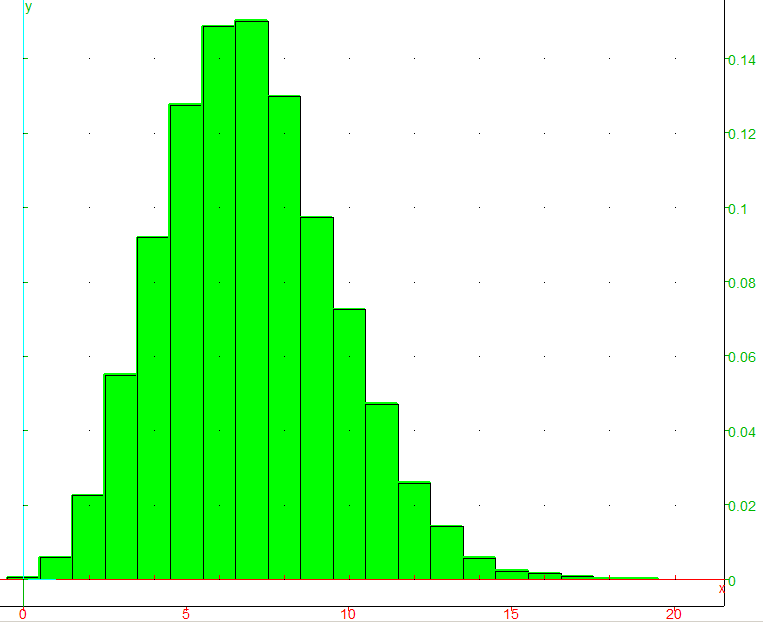
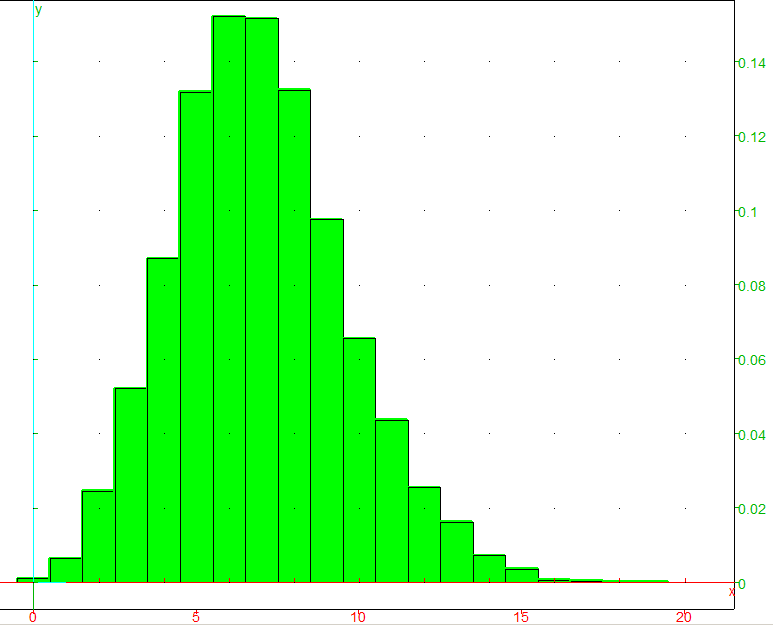
Lecture : en abscisse est placé le nombre de paquets arrivés (centre de l'intervalle) tandis que l'ordonnée correspond à la fréquence où ce nombre est obtenu lors de la simulation de 10000 simulations.
-
Obtient-on toujours le même histogramme ?
-
Pourqoui ?
-
Les histogrammes semblent-ils grandement différés ?
-
-
On cherche à approcher l'histogramme obtenu avec le programme précédent par une loi particulière. Voici la représentation graphique de l'histogramme précédent superposé de la loi dite "de Poisson de paramètre 7".
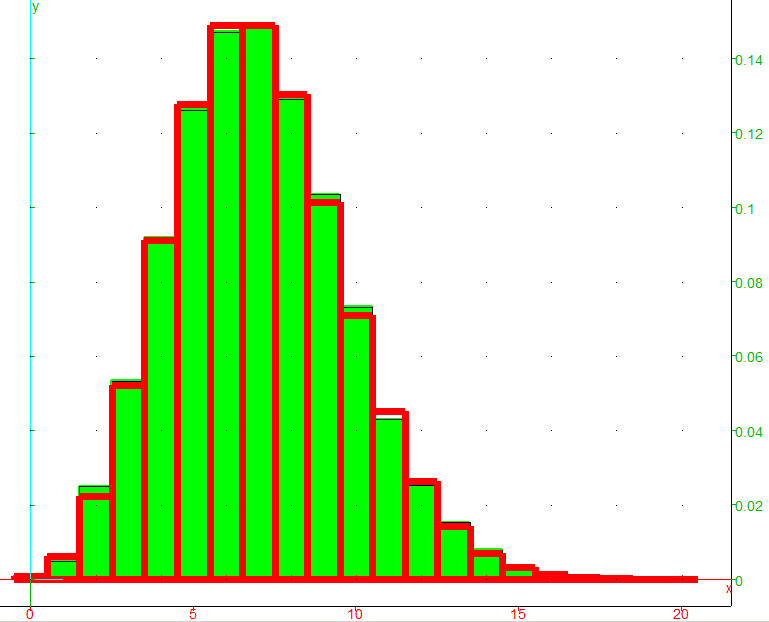
Ce graphique est issu de la simulation obtenue sur Xcas avec ce fichier.
Que pensez-vous de cette approximation ?
La loi de Poisson correspond au nombre de réalisations observées, durant un intervalle de temps
de longueur donnée,
lorsque le temps d’attente entre deux réalisations est fourni par une loi exponentielle.
Le paramètre de cette loi de Poisson correspond à la moyenne du nombre de réalisations observées.
Cette loi a été introduite par Siméon Denis Poisson
en 1837 pour décrire la somme de plusieurs phénomènes aléatoires
de faible probabilité et indépendants les uns des autres.
Quand un événement est a une faible probabilité, le nombre d’observations de cet événement au cours
d’un grand nombre d’expériences indépendantes suit approximativement la loi de Poisson.
Définition et propriétés
Une variable aléatoire $X$ suit la loi de Poisson $P(\lambda)$ de paramètre $\lambda$ strictement positif
lorsque sa loi de probabilité est définie par :
pour tout nombre entier naturel $k$ : $P(X=k)=e^{-\lambda}\dfrac{\lambda^k}{k!}$,
où $k!$ est tel que $0!=1$ et pour tout entier naturen non nul $n$, $n!=n\times (n-1)\times...\times 2\times 1$.
Pour calculer une probablité liée à une loi de Poisson, vous pourrez cette année :
-
soit utiliser directement la formule précédente afin d'obtenir la valeur exacte,
-
soit utiliser Geogebra (ou Xcas), afin d'obtenir une valeur approchée.
Utilisation de Geogebra
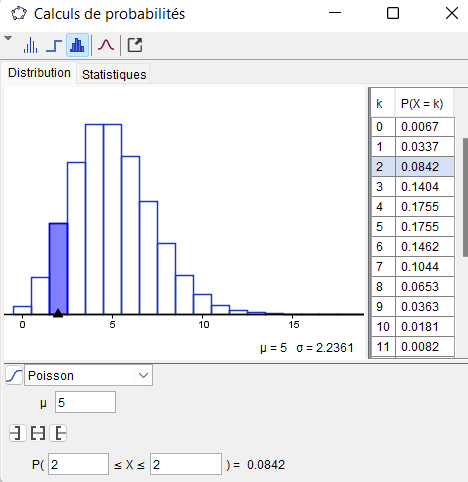
Si $X$ suit une loi de Poisson de paramètre $\lambda=5$, alors pour calculer $P(X=2)$, il suffit :
-
dans Geogebra, ouvrir Calculs de probabilités à partir de l'onglet affichage.
-
Sélectionner la loi de Poisson.
-
Saisir comme valeur du paramètre $\mu$ le nombre ici 5.
-
Cliquer à droite du graphique sur la ligne correspondant à la valeur de $k$ voulue. Ici, 2.
-
Il suffit alors de lire la valeur approchée proposée par Geogebra ; ici 0.0842.
On reprend la variable aléatoire $X$ suivant la loi de Poisson de paramètre $\lambda=5$.
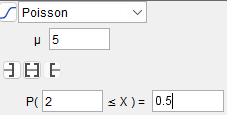
Pour trouver une borne de l'intervalle liée à une probabilité fixée,
par exemple pour trouver le réel $a$ stritement positif tel que $P(X\ge a)=0.5$, il suffit de
remplacer les deux dernières étapes de l'exemple précédent par :
-
Sélectionner le type d'intervalle correspondant à celui recherché. Ici,
 pour $X\ge a$.
pour $X\ge a$.
-
Saisir la probabilité connue. Ici 0.5.
-
Il suffit alors de lire la valeur approchée proposée par Geogebra pour $a$ ; ici 5.
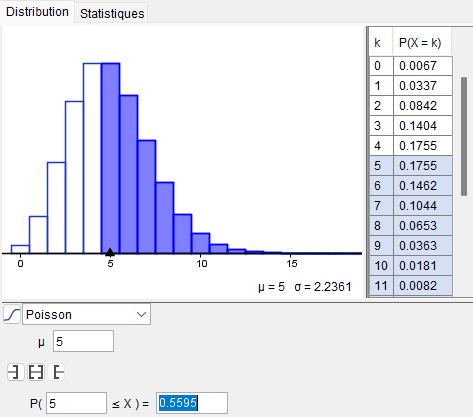
Comme la loi est discrète, il n'existe pas d'entier $k$ qui permet d'obtenir exactement la probabilité voulue ; Geogebra cherche ainsi le plus petit entier dont la probabilité dépasse ici 0.5.
Une fois cette entier trouvé, il calcule la probabilité approchée liée à cet entier et remplace la saisie que vous avez effectuée par cette valeur approchée.
Ainsi, dans cet exemple, 0.5 a été remplacé automatiquement par 0.5595.
Il est possible d'obtenir ces valeurs directement avec Xcas, mais sans la représentation graphique qui permet de faciliter la vérification de la cohérence :
-
poisson(λ,k)renvoie la probabilité $P(X=k)$, c'est-à-dire $e^{-\lambda}\dfrac{\lambda^k}{k!}$, lorsque $X$ suit une loi exponentielle de paramètre $\lambda$. -
poisson_cdf(λ,k)renvoie la probabilité $P(X\le k)$, lorsque $X$ suit une loi exponentielle de paramètre $\lambda$. -
poisson_icdf(λ,p)renvoie le réel $h$ tel que $P(X\le h)=p$, lorsque $X$ suit une loi exponentielle de paramètre $\lambda$.
Suite à une étude statistique, une société de services informatiques constate qu'elle reçoit chaque jour en moyenne un appel
toutes les 10 minutes.
On désigne par $X$ la variable aléatoire qui donne le nombre d'appels reçus un jour donné entre 10h et 11h.
On admet que $X$ suit une loi de Poisson de paramètre $\lambda=6$.
-
Déterminer la probabilité pour qu'il y ait exactement 6 appels entre 10h et 11h ce jour donnné.
-
Déterminer la probabilité pour qu'il y ait exactement aucun appel entre 10h et 11h ce jour donnné.
-
Déterminer la probabilité pour qu'il y ait entre un et neuf appels entre 10h et 11h ce jour donnné.
-
Déterminer la probabilité pour qu'il y ait au moins trois appels entre 10h et 11h ce jour donnné.
-
Déterminer la probabilité pour qu'il y ait au plus huit appels entre 10h et 11h ce jour donnné.
-
Déterminer le nombre $n$ tel que la probabilité qu'il y ait strictement plus que $n$ appels entre 10h et 11h ce jour donnné soit inférieure à 0.01.
Soit $X$ une variable aléatoire suivant la loi de Poisson $P(\lambda)$, c'est-à-dire de paramètre $\lambda$.
-
Son espérance mathématique est donnée par : $\displaystyle E[X]= \lambda$.
-
Sa variance est donnée par : $\displaystyle V[X]= \lambda$.
-
Son écart-type est donné par : $\sigma[X]=\sqrt{V(X)} = \sqrt{\lambda}$.
La valeur approchée de la moyenne et de l'écart-type sont directement lisibles dans le coin inférieur droit de la fenêtre de Geogebra ; la moyenne correspondant à $\mu$ et l'écart-type correspondant à $\sigma$.
On considère le nombre de clients se présentant au guichet d’un bureau de poste par intervalle de temps
de durée 10 minutes entre 14h30 et 16h30. Ce nombre est mesuré par la variable aléatoire $X$.
Il a été mesuré qu’en moyenne 7 personnes se présentent au guichet sur un intervalle de 10 minutes.
On admet que la variable aléatoire $X$ suit la loi de Poisson de paramètre $\lambda$.
-
Comme en moyenne 7 personnes se présentent au guichet sur un intervalle de 10 minutes, quelle est la valeur du paramètre $\lambda$ ?
-
Calculer une valeur approchée de la probabilité qu’entre 16h et 16h10, 8 personnes au moins se présentent à ce guichet.
-
Calculer l'écart-type $\sigma$ de $X$.
-
Déterminer le plus petit intervelle $[a;b]$ contenant l'intervalle $[\lambda-2\sigma;\lambda+2\sigma]$, tel que $a$ et $b$ sont deux entiers naturels.
-
Déterminer la probabilité qu'il ait entre $a$ et $b$ personnes se présentant au guichet entre 16h et 16h10.
On considère le nombre $X$ d’appels à un standard téléphonique pendant une heure. On observe que :
-
il y a rarement deux appels simultanés ;
-
le nombre d’appels sur une période donnée ne dépend que de la durée de la période ;
-
les appels sont indépendants les uns des autres.
On peut alors dire que $X$ suit une loi de Poisson.
Le standard reçoit en moyenne 10 appels par heure.
-
Déterminer la valeur du paramètre $\lambda$.
-
Déterminer la probabilité d’avoir sept appels sur une période d’une heure.
-
Calculer la probabilité qu’il y ait au moins 15 appels en une heure.
-
Dans 95% des cas, combien d’appels va recevoir le standard au maximum ?
Comparaisons d’une loi binomiale par une loi de Poisson
Approximation d’une loi binomiale par une loi de Poisson
Voici la représentation graphique de la loi de Poisson de paramètre $\lambda=5$ :
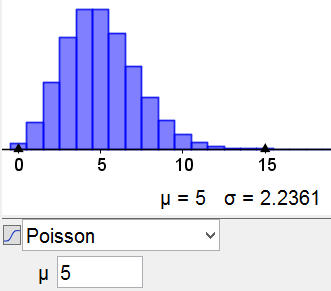
À quelle loi vous fait penser l'allure de la courbe ?
Comparons donc ces deux lois.
Dans une entreprise, on considère que la probabilité d’obtenir un article défectueux à la sortie d’une
chaîne de fabrication est $p=0.05$. Lors d’un contrôle de qualité, on envisage de prélever un échantillon de 120 articles.
Bien que ce prélèvement soit exhaustif, nous considérons que la production est suffisamment importante pour
qu’on puisse assimiler ce prélèvement à 120 tirages avec remise, donc indépendants, d’un article non défectueux ou non.
On note $X$ la variable aléatoire mesurant le nombre d’articles défectueux d’un tel échantillon de 120 articles.
-
Déterminer la loi suivie par la variable $X$.
-
Calculer $E(X)$.
-
Grâce à un tableur, on a obtenu le tableau des premières valeurs de la loi suivie par $X$ :

Voici ci-dessous, une table des valeurs de la loi de Poisson suivant différentes valeurs du paramètre $\lambda$ :
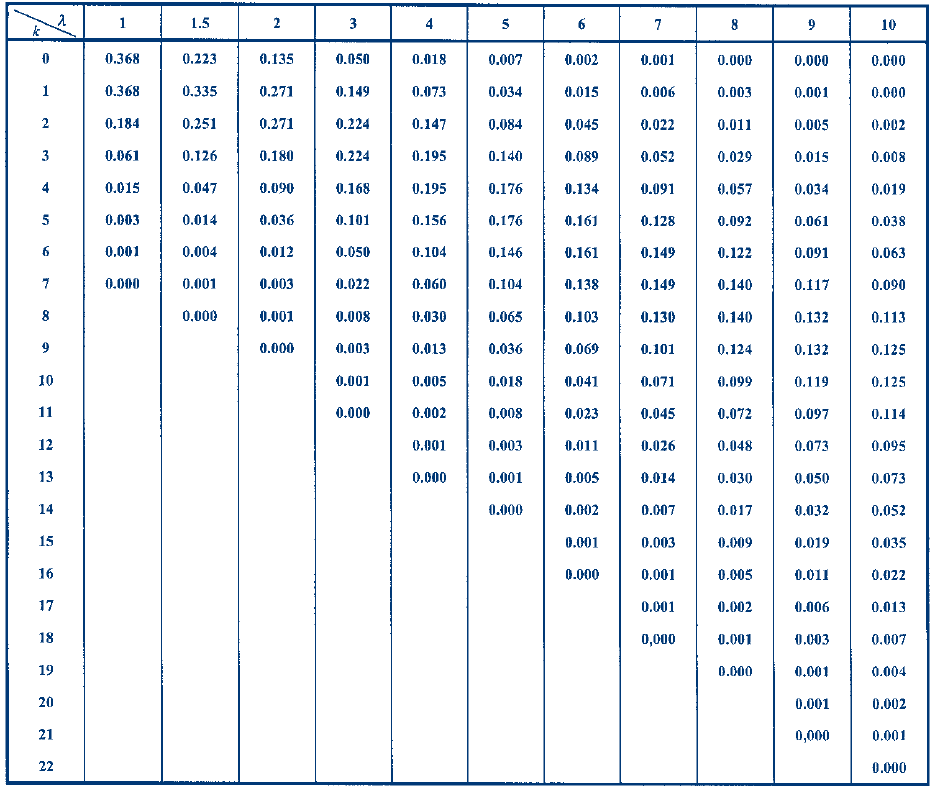
Trouver une valeur du paramètre $\lambda$ telle que les valeurs de la loi suivie par $X$ et de celles de la loi de Poisson de paramètre $\lambda$ soient proches.
-
Voici différentes comparaisons entre la loi binomiale de paramètres $n$ et $p$ et de celle de Poisson de paramètre $\lambda = n\times p$ :
 L'approximation de la loi binomiale de paramètres $n$ et $p$ par la loi de Poisson de paramètre $\lambda=n\times p$
est-elle toujours pertinente ?
L'approximation de la loi binomiale de paramètres $n$ et $p$ par la loi de Poisson de paramètre $\lambda=n\times p$
est-elle toujours pertinente ?
-
Voici une animation Geogebra permettant visuellement de comparer les deux lois : Proposez des critères sur $n$ et sur $p$ qui semblent assurer que l'on puisse assurer l'approximation d'une loi binomiale de paramètres $n$ et $p$ par une loi de Poisson de paramètre $\lambda$.
Si $n$ est "grand" et $p$ "voisin" de 0 et $np$ pas "trop grand" alors la loi binomiale $\mathcal{B}(n;p)$ est très proche de la loi de Poisson $\mathcal{P}(\lambda)$ où $\lambda=n\times p$.
Plus rigoureusement, il suffit $n\ge 30$, $p\le 0.1$, $np\le 15$ ou $n\ge 50$, $p\le 0.1$ et $np\le 10$.
L'intérêt de cette approximation est que l'on remplace une loi à deux paramètres ($n$ et $p$) par une loi à un
seul paramètre ($\lambda$) tout en conservant exactement l’espérance mathématique.
Cette approximation était très utile avant l'apparition d'outils numériques.
Domaines d'application de ces deux lois
Les lois binomiale et de Poisson sont deux lois discrètes.
Il est important que vous ne confondiez ni leurs conditions différentes d'utilisation, ni leurs domaines d'application.
Pour la loi binomiale
Pour pouvoir modéliser un phénomène aléatoire à l'aide d'une loi binomiale, il faut :
-
qu'il n'ait que deux résultats possibles (appelés "succès" et "échecs"),
-
des répétitions dans des conditions identiques et indépendantes,
-
la variable aléatoire compte le nombre de succès (ou d'échecs).
Modèle d'application :
Tout problème équivalent à un problème de tirages successifs avec remise.
Pour la loi de Poisson
Pour pouvoir modéliser un phénomène aléatoire à l'aide d'une loi de Poisson, il faut :
-
qu'il soit très rare d'avoir deux succès simultanément,
-
le nombre moyen de succès pendant une période $T$ ne dépend que de la durée $T$,
-
l’arrivée d’un succès est indépendante du précédent.
Modèle d'application :
Tout problème où le futur est indépendant du passé.
Voici quelques exemples de domaines où cette loi de Poisson est utilisée :
-
elle est surtout utilisée pour l'étude d'événements rares (accidents, ...),
-
dans les télécommunications (pour compter le nombre de communications dans un intervalle de temps donné),
-
dans le contrôle de qualité statistique (nombre de défauts),
-
dans la description de certains phénomènes liés à la désintégration radioactive,
-
dans la finance (défaut de crédit),
-
dans le transport aérien (estimation de la demande de passagers), ...
Exercices
-
Soit $X$ une variable aléatoire qui suit la loi de Poisson de paramètre 9.
Déterminer la probabilité $P(X\ge 12)$. -
Soit $X$ une variable aléatoire qui suit la loi de Poisson de paramètre 8.
Déterminer la plus petite valeur de $k$ vérifiant : $P(X\le k)\ge 0.8$.
Soit $X$ une variable aléatoire qui suit une loi de Poisson.
Déterminer à $10^{-3}$ près le paramètre $\lambda$ sachant que $P(Y=0)=0.3$.
S'aider de la formule permettant de calculer de manière exacte une probabilité, formule présente dans la définition de la loi de Poisson.
Dans une banque, qui est ouverte sans interruption à midi, une étude statistique a montré que, lors de la
pause déjeuner du personnel (par rotation entre 12h et 13h), le taux moyen d’arrivée est de 8 clients par
heure le lundi.
$X$ est la variable aléatoire qui compte le nombre de clients se présentant à la banque entre 12h et 13h un lundi.
On admet que $X$ suit une loi de Poisson.
-
Quel est le paramètre de cette loi ?
-
Quelle est la probabilité pour que la banque reçoive 10 clients entre 12h et 13h un lundi ?
-
Quelle est la probabilité pour que la banque reçoive plus de 15 clients entre 12h et 13h un lundi ?
-
Dans au plus 95% des cas, quel est le nombre de clients reçus au maximum entre 12h et 13h un lundi ?
Le nombre moyen de clients qui se présentent à la caisse d'un kiosque de centre ville sur un intervalle de 10 minutes est de 15.
Quelle est la probabilité qu'aucun client ne se présente à la caisse dans un intervalle de 3 minutes ?
Une compagnie d'assurances assure un parc de 200 véhicules contre un risque qui a une probabilité égale à 0.5% de survenir.
Chaque véhicule rapporte 160€ à la compagnie tandis que la compagnie verse 10000€ par sinistre.
On admet que la variable aléatoire $Y$ qui à tout parc de 200 véhicules associe le nombre de sinistres suit la loi de
Poisson de paramètre $\lambda$.
On appelle $X$ la variable aléatoire qui au nombre de sinistres fait correspondre
la somme acquise ou due par la compagnie.
-
Déterminer la valeur de $\lambda$.
-
Calculer $P(X=2000)$.
-
Quelle est la probabilité que la compagnie réalise un bénéfice ?
-
Exprimer la variable aléatoire $X$ en fonction de la loi variable aléatoire $Y$.
-
Quelle est l'espérance de gain pour la compagnie d'assurance ?
Une entreprise fabrique un certain type de jouets électroniques.
On admet que la probabilité que la durée de vie d’un tel jouet, prélevé au hasard dans la production,
soit strictement supérieure à 29.8 milliers d’heures est 0.025.
On note $Y$ la variable aléatoire qui, à tout échantillon aléatoire de 160 jouets, associe le nombre de jouets dont
la durée de vie est strictement supérieure à 29.8 milliers d’heures.
-
Justifier que $Y$ suit une loi binomiale dont on déterminera les paramètres.
-
Déterminer les valeurs de $E(Y)$ et de $\sigma(Y)$.
-
On admet qu’on peut approcher la loi de probabilité de $Y$ par une loi de Poisson.
Donner son paramètre $\lambda$. -
Déterminer le plus petit entier $n$ tel que : $P(Y\le n)\ge 0.9$.
Une société s’occupe de la saisie informatique de documents.
Pour chaque document, une première saisie est retournée, pour vérification, au client correspondant.
Les résultats demandés seront données sous forme de valeurs décimales arrondies à $10^{-3}$.
Pour chaque document, le délai de retour de la première saisie vers le client est fixé à 2 semaines.
Une étude statistique a montré que la probabilité qu’une saisie prélevée au hasard soit effectivement retournée au client
dans le délai fixé est égale à 0.9.
On désigne par $X$ la variable aléatoire qui, à tout échantillon de $n$ saisies prélevés au hasard par tirage avec remise,
associe le nombre de saisies pour lesquelles le délai de retour n’a pas été respecté.
-
-
Quelle est la loi suivie par la variable aléatoire $X$ ?
-
Pour cette question, on suppose que $n=100$. Calculer la probabilité $P(X=8)$.
-
-
Pour cette question, on suppose que $n=100$.
On admet que la loi de probabilité de $X$ peut être approchée par une loi de Poisson.-
Donner la paramètre de cette loi de Poisson.
On note désormais $Y$ une variable aléatoire suivant la loi de Poisson définie à cette question.
-
Calculer une valeur approchée de chacune de la probabilité $P(Y=10)$.
-
Calculer une valeur approchée de chacune de la probabilité $P(Y \gt 12)$.
-
Demander le programme !
-
La formule donnant l'espérance mathématique d'une loi de Poisson de paramètre $\lambda$.
-
La formule donnant l'écrat-type d'une loi de Poisson de paramètre $\lambda$.
-
Le fait que l'on peut approcher une loi binomiale par une loi de Poisson dans certains cas.
-
La signification de l'espérance mathématique d'une loi de Poisson.
-
Savoir calculer sur Geogebra une probabilité liée à une loi de Poisson.
-
Savoir calculer sur Geogebra la borne d'un intervalle connaissant la probabilité asssociée à cet intervalle.
-
Savoir retrouver sur Geogebra une valeur approchée de l'espérance mathématique et de l'écart-type d'une loi de Poisson de paramètre $\lambda$.
-
Savoir déterminer le paramètre de la loi de Poisson approchant une loi binomiale donnée.
-
Savoir interpréter concrètement l'espérance mathématique d'une loi de Poisson.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International