Les algorithmes de tris sont dans la section Algorithmique.
- Contenus : tris par insertion, par sélection
- Capacités attendus : écrire un algorithme de tri. Décrire un invariant de boucle qui prouve la correction des tris par insertion, par sélection.
- Commentaires : la terminaison de ces algorithmes est à justifier. On montre que leur coût est quadratique dans le pire cas.
Tri par insertion
Un cas concret
Commençons par trier à la main un jeu de carte !
Cinq cartes vous ont été distribuées et vous les retournez une à une pour les ranger par ordre croissant dans votre main.
La première carte retournée est :

La deuxième carte retournée est :

Vous mettez cette carte à droite en tant que plus grosse ; votre main triée est alors :


La troisième carte retournée est :

Vous insérez cette carte entre le 5 et le 10 ; votre main triée est alors :



La quatrième carte retournée est :

Vous insérez cette carte entre le 8 et le 10 ; votre main triée est alors :




La dernière carte retournée est :

Vous insérez cette carte au debut ; votre main triée est alors :





Ainsi la liste des valeurs des cinq cartes obtenues [5, 10, 8, 9, 2] a été triée par des insertions successives en [2, 5, 8 , 9, 10] :





Tri par insertion
Ce tri correspond au tri de cartes généralisé avec une liste de valeurs.
On considère les éléments de la liste un par un (comme pour les cartes) :
-
le premier élément de la liste forme une liste triée à un seul élément,
-
le deuxième élément de la liste initiale est rangée à sa place dans la liste triée : on a désormais une liste triée à deux éléments,
-
le troisième élément de la liste initiale est rangée à sa place dans la liste triée : on a désormais une liste triée à trois éléments,
- ...
-
le dernier élément de la liste initiale est rangée à sa place dans la liste triée : on a désormais complètement trié la liste initiale.
Voici le pseudo-code en langage naturel de ce tri :
tri_insertion(liste L indexée de 0 à n-1) Pour i allant de 1 à n-1 faire placer l'élément L[i] dans la liste déjà classée L[0:i-1] retourner la liste L
Pour placer au bon endroit l'élément L[i], il suffit de permuter cet élément avec le précédent dans la liste triée tant que cet élément précédent est plus grand (et qu'il existe !).
Voici donc le tri par insertion écrit en langage Python :
def tri_insertion(lst: list) -> list:
for i in range(1, len(lst)):
elt = lst[i]
j = i
while j > 0 and elt < lst[j-1]:
lst[j] = lst[j-1]
j -= 1
lst[j] = elt
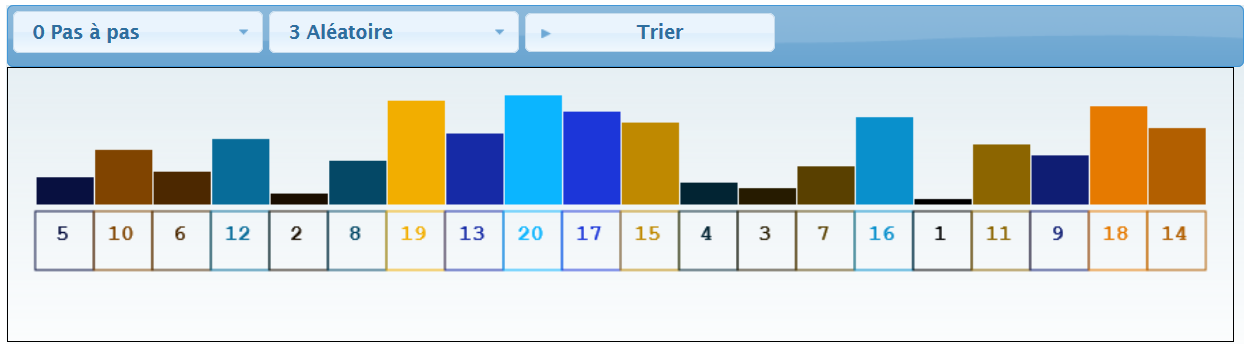
return lstPour visualiser comment cet algorithme trie une liste quelconque, accéder à un site Web en cliquant sur l'image ci-dessous :
Un fois accédé.e à ce site, cliquer sur Trier pour lancer l'application.
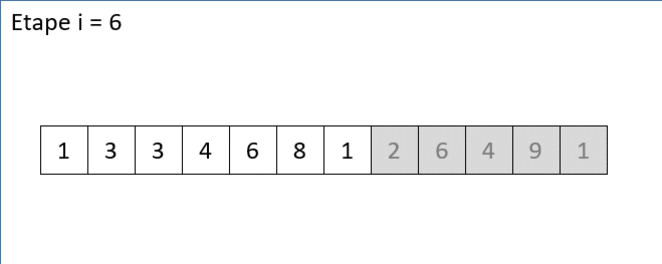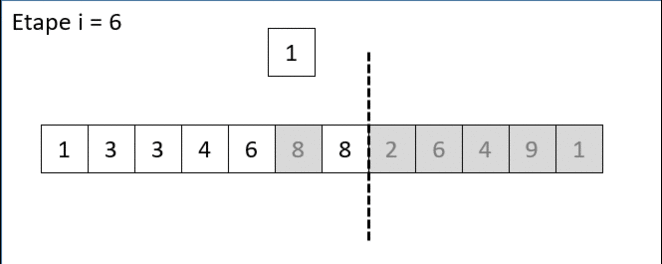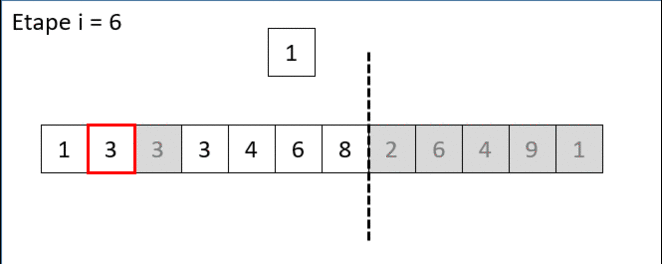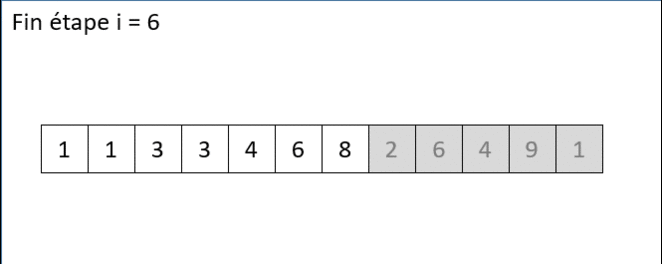
Voici ci-dessous une animation gif qui illustre où positionner le nombre 1 en position d'index 6 de la liste [1,3,3,4,6,8,1,2,6,4,9,1] sachant que les 6 premiers nombres [1,3,3,4,6,8] sont déja triés :
La première fonction de tri implémentée sur ordinateur serait le fait de l'informaticienne Betty Holberton qui a travaillé pendant la seconde Guerre Mondiale sur le premier ordinateur électronique : l'ENIAC
Voici une visualisation de l'algorithme de tri par insertion avec une danse roumaine :
Si vous n'avez pas un accès direct à Python, il est possible de vous servir du Trinket
accessible avec ce lien pour saisir et tester temporairement votre code.
Ah ! Les joies d'un bac à sable !
Proposer des commentaires au niveau du code de la fonction tri_insertion.
Voici une liste de nombres à trier : [4, 9, 6, 7, 12, 3, 4].
Écrire la trace d'exécution de la fonction tri_insertion précédente en faisant apparaître les valeurs de i et de j considérées, l'élément à classer, la liste des éléments déjà triés et la liste complète
(en partie) triée en complétant un tableau comme ci-dessous :
| Valeur de $i$ | Valeur de $j$ | Élément à trier | Liste déjà triée | Liste complète |
|---|---|---|---|---|
| 1 | 1 | 9 | [4] | [4,9,6,7,12,3,4] |
| ... | ... | ... | ... | ... |
Complexité
Vous allez désormais calculer la complexité de l'algorithme de tri par insertion, rappelé ci-dessous, dans le pire des cas, c'est à dire dans le cas où toutes les valeurs sont triées dans l'ordre décroissant.
def tri_insertion(lst: list) -> list:
for i in range(1, len(lst)): # le premier élément forme seul une liste classée
elt = lst[i] # élément à classer
j = i
while j > 0 and elt < lst[j-1]: # permutation avec le précédent s'il est plus grand
lst[j] = lst[j-1]
j -= 1
lst[j] = elt # placement au bon endroit
return lstSocrative sur la complexité.
vidéo correctrice :Le tri par insertion est un tri qui semble naturel et facile à implémenter.
Son coût dans le cas le pire est quadratique. Toutefois, il offre de bons résultats sur des listes de peu d'éléments ou partiellement triées.
Le coût du tri par insertion est quadratique dans le pire des cas, c'est-à-dire lorsque la liste est triée par ordre décroissant.
La plus ancienne trace connue de données triées (afin de faciliter la recherche de valeurs) est la tablette
babylonienne d'Inakibit-Anu datant d'environ -200 avant notre ère.
(source)
Cette tablette contient 500 nombres ainsi que leur inverse écrits en base 60.
Les premières machines à trier automatiques sont apparues aux États-Unis à la fin du $XIX^e$ siècle. Elles ont été utiliser pour traiter plus rapidement les recensements (cf. recensement de 1890 )
Lors de l'apparition des ordinateurs vers 1945, les algorithmes de tri font partie des tout premiers programmes informatiques
développés.
Du fait de leur forte utilité, de nombreux algorithmes algorithme de tri ont été développés, surtout dans les années 1950 et 1960.
L'analyse de la complexité de ces algorithme de tri permet de comparer l'intérêt de chaque algorithme, en plus d'autres critères comme
le fait d'être stable (préservation de l'ordre initial entre éléments de même valeur),
le fait de prendre peu de place en mémoire pour fonctionner (complexité en espace), le
fait de pouvoir être partagé entre différents cœurs du processeur (parallélisation).
L'algorithme de tri implémenté dans l'interpréteur Python est le Timsort inventé en 2002 par
Tim Peters.
Il est un mélange entre le tri par insertion et le tri par fusion
qui sera étudié en terminal.
Le langage Python dispose d'une fonction et d'une méthode natives pour trier les listes :
-
sorted(lst)renvoie une liste triée (par ordre croissant) formée des éléments de la listelst; la listelstn'est elle pas modifiée. -
lst.sort()ne renvoie rien mais modifie la listelsten la triant par ordre croissant.
Exercices
Trouver dans les codes suivants des erreurs puis les corriger.
Premier code
def tri_1(liste):
n = len(liste)
i = 1
while i < n:
x = liste[i]
j = i
while liste[j-1] > x :
liste[j] = liste[j-1]
j = j-1
liste[j] = x
i = i+1
return liste Deuxième code
def tri_2(liste):
for i in range(1, len(liste)):
x = liste[i]
j = i
while j > 0 and liste[j-1] > x:
liste[j] = liste[j-1]
liste[j] = x
return liste Troisième code
def tri_3(liste):
i = 1
for i in range(1, len(liste)):
x = liste[i]
for j in range(i, len(liste)):
if liste[j-1] > x:
liste[j] = liste[j-1]
liste[j] = x
return liste Quatrième code
def tri_4(liste):
n = len(liste)
i = 1
while i < n:
x = liste[i]
j = i
while j> 0 and liste[j-1] > x:
j = j-1
liste[j] = liste[j-1]
liste[j] = x
i = i+1
return listeÀ partir du script vu précédemment, que renvoie la fonction tri_insertion si vous donnez comme paramètres d'entrée la liste suivant :
lst = ['poire', 'pomme', 'abricot', 'kiwi', 'orange', 'noix', 'noisette', 'cerise', 'brugnon', 'nectarine', 'prune', 'groseille', 'framboise']-
Proposer en langage Python une fonction
est_triequi reçoit comme entrée une liste non vide et qui renvoie un booléen valantTruesi la liste entrée est triée par ordre croissant etFalsesinon. -
Testez votre programme avec les listes suivantes :
puis :lst = [4, 8, 9, 10, 10, 15]lst = [4, 10, 9, 10, 15]
Voici ci-dessous le code d'une fonction mystère
def mystere(tab, valeur):
"""
: param tab (list) liste d'entiers triée par ordre croissant
: param valeur (int) - entier
: return (list)
Sortie : ......................................................................................................
"""
return [x for x in tab if x < valeur] + [valeur] + [x for x in tab if x >= valeur]-
Que renvoie l'appel
mystere([2, 4, 6, 6, 7, 9], 7)? -
Que renvoie l'appel
mystere([2, 4, 6, 6, 7, 9], 1)? -
Que renvoie l'appel
mystere([2, 4, 6, 6, 7, 9], 10)? -
Compléter la ligne "Sortie : ..."" de la documentation afin d'expliciter le rôle de la fonction mystere.
Adapter le programme de tri par insertion pour avoir une fonction tri_insertion_decroissante
renvoyant la liste entrée comme paramètres ordonnée par ordre décroissant.
Le tri par insertion est un algorithme qui s'inspire de la façon dont on peut trier une poignée de cartes. On commence avec une seule carte dans la main gauche (les autres cartes sont en tas sur la table) puis on pioche la carte suivante et on l'insère au bon endroit dans la main gauche.
-
Voici une implémentation en Python de cet algorithme. Recopier et compléter les lignes 6 et 7 (uniquement celles-ci) :
1 def tri_insertion(liste): 2 """ trie par insertion la liste en paramètre """ 3 for indice_courant in range(1, len(liste)): 4 element_a_inserer = liste[indice_courant] 5 i = indice_courant - 1 6 while i >= 0 and liste[i] > ................................ : 7 liste[...........] = liste[...........] 8 i = i - 1 9 liste[i + 1] = element_a_inserer -
On a écrit dans la console les instructions suivantes :
notes = [8, 7, 18, 14, 12, 9, 17, 3] tri_insertion(notes) print(notes)On a obtenu l'affichage suivant :
[3, 7, 8, 9, 12, 14, 17, 18].On s'interroge sur ce qui s'est passé lors de l'exécution de
tri_insertion(notes).-
Donner le contenu de la liste notes après le premier passage dans la boucle
for. -
Donner le contenu de la liste notes après le troisième passage dans la boucle
for.
-
-
Quelle est la complexité en temps du tri par insertion dans le pire des cas ?
-
Le tri par insertion est une méthode pour trier les valeurs d'un tableau (= liste en Python) par ordre croissant.
-
Pour une une liste de taille $n$, le tri par insertion consiste à répéter de l'indice (=position) $i=1$ jusqu'à celle $i=n-1$ les opération suivantes :
-
Repérer la valeur de l'élément en position $i$ le premier élément de la zone non triée :
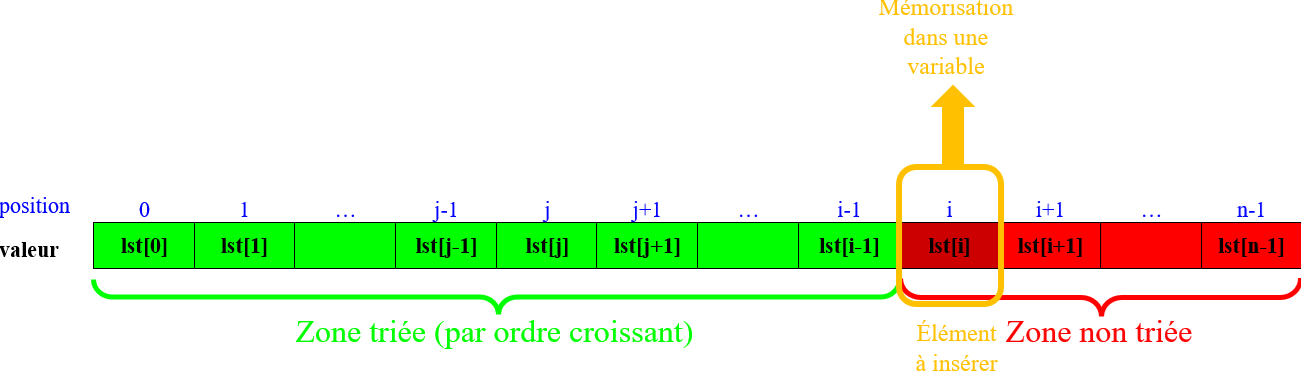
-
Comparer cette valeur avec celles de la zone triée à partir de la plus grande :
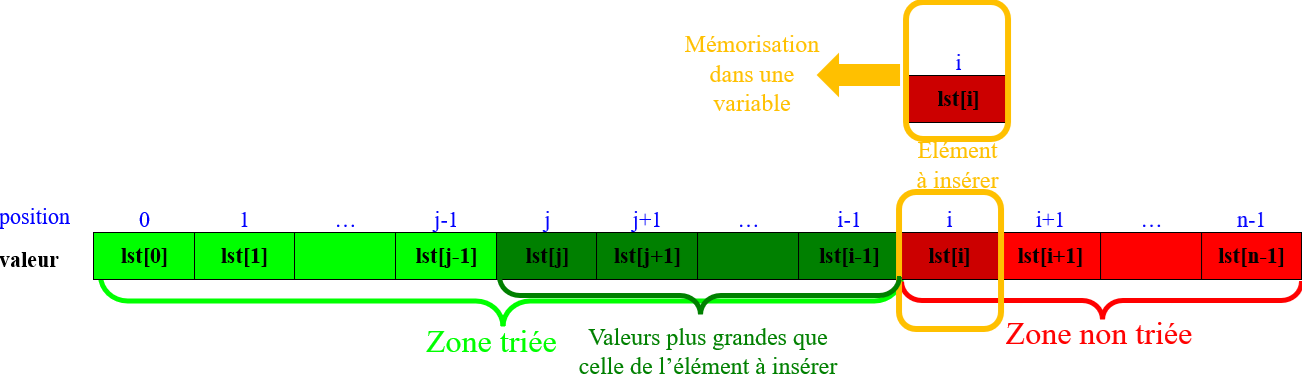
-
Décaler chaque valeur supérieure de la zone triée d'un rang vers la droite :
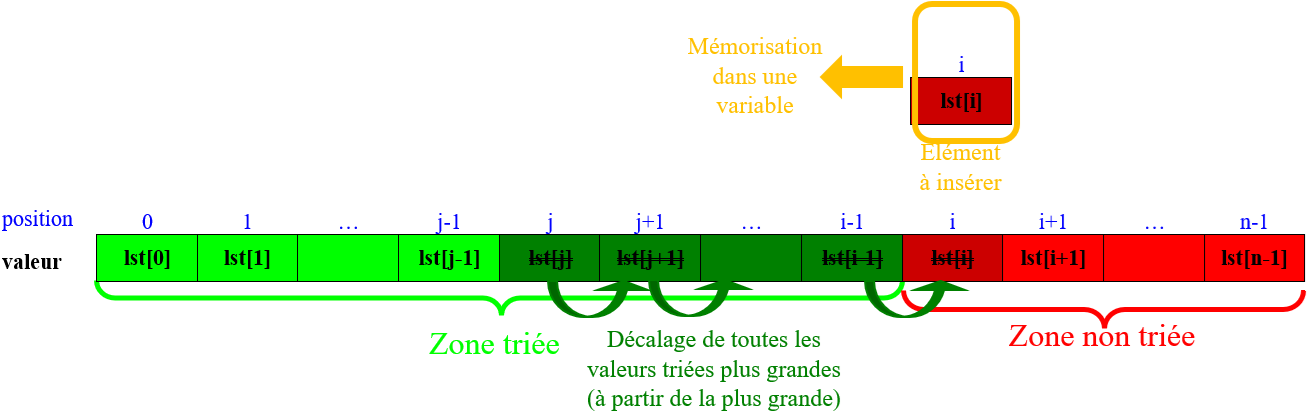
-
Placer l'élément à insérer correctement dans la zone triée, désormais agrandie :
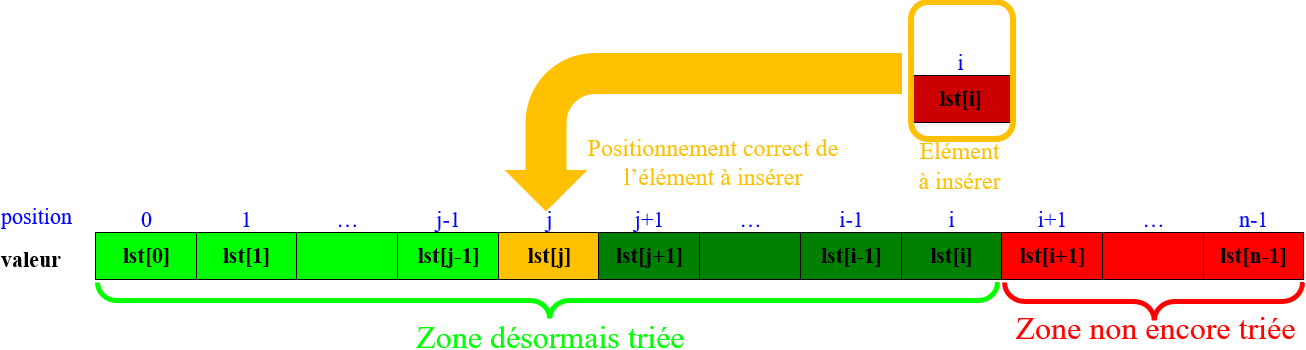
-
-
Une écriture du tri par insertion en Python est :
def tri_insertion(lst: list) -> list: for i in range(1, len(lst)): elt = lst[i] j = i while j > 0 and elt < lst[j-1]: lst[j] = lst[j-1] j -= 1 lst[j] = elt return lst -
Le coût en temps d'exécution du tri par insertion est quadratique dans le pire des cas et en moyenne.
Voici un exercice à faire en autonomie pour tester votre maîtrise sur
l'insertion d'un nombre dans une liste triée.
Cet exercice est issu du site collaboratif de la forge.
Voici un exercice à faire en autonomie pour tester votre maîtrise sur
le tri par insertion.
Cet exercice est issu du site collaboratif de la forge.
Tri par sélection
Un cas concret
Recommençons par trier un jeu de carte à la main !
Cinq cartes vous ont été distribuées et vous les avez toutes dans un ordre quelconque dans votre main.
Supposons que les cartes en main soient :





Pour trier les cartes, l'idée est de :
-
balayer l'ensemble des cartes non encore triées afin d'y repérer la plus petite.
-
Cette plus petite carte restante est alors placée en première position des cartes pas encore triées.
Mise en œuvre de la démarche sur l'ensemble des cinq cartes :
Aucune carte n'a déjà été triée. Parmi les 5 de l'ensemble, la plus petite est le 2 (de carreau) :





Cette carte de valeur minimale est placée en première position par une permutation de deux cartes, d'où la nouvelle configuration :





Le 2 est déjà bien placé. Parmi les 4 cartes restantes, la plus petite est le 5 (de cœur) : par hasard, il est déjà bien placé :





Deux cartes sont déjà bien placées. Parmi les 3 cartes restantes, la plus petite est le 8 (de carreau) :





Cette carte restante de valeur minimale est placée en première position des cartes restantes par une permutation de deux cartes, d'où la nouvelle configuration :





Trois cartes sont déjà bien palcés. Parmi les 2 cartes restantes, la plus petite est le 9 (de pique) :





Cette carte restante de valeur minimale est placée en première position des cartes restantes par une permutation de deux cartes, d'où la nouvelle configuration :





La dernière carte restante non triée est forcément la plus grande de toutes : aucun nouveau changement n'est nécessaire pour obtenir finalement la liste entièrement triée :





Tri par sélection
On considère les éléments de la liste un par un (comme pour les cartes) :
-
le plus petit élément de la liste est mis en première position par permutation ; on a désormais un début de liste triée à un élément,
-
le deuxième plus petit élément de la liste est rangé en seconde position par permutation ; on a désormais un début de liste triée à deux éléments,
- ...
-
l'avant dernier plus petit élément de la liste est rangé en avant-dernière position par permutation : on a désormais complètement trié la liste initiale.
Voici le pseudo-code en langage naturel de ce tri :
tri_selection(liste L indexée de 0 à n-1) Pour i allant de 0 à n-2 faire trouver le plus petit élement L[j] de la liste entre i et n-1 échanger les éléments L[i] et L[j] retourner la liste L
Deux fonctions seront utiles pour écrire en python cet algorithme :
-
la fonction
get_position_minqui renvoie l'index du minimum d'une liste entre un index nommédepartet son dernier terme. Cette liste et l'indexdepartsont entrés comme paramètres. -
la fonction
echangerqui permute deux éléments d'une liste extraite entrée comme paramètre, les deux index de ces éléments étant aussi entés comme paramètres.
get_position_min reçoit deux paramètres en entrée :
-
lstqui est la liste étudiée, -
departqui un nombre entier qui correspond à un index.
get_position_min renvoie l'index du minimum de la liste extraite entrée dont les termes sont compris entre l'index depart et le dernier.
Voici le code de la fonction get_position_min où deux lignes sont incomplètes :
def get_position_min(lst: list, depart: int) -> int:
pos = depart # pos stocke la position du minimum : lst[pos] sera donc le minimum trouvé
i = pos + 1
while i < len(lst):
.......................... # ligne 5
.......................... # ligne 6
i += 1
return pos Compléter le code des lignes 5 et 6 de la fonction get_position_min
Voici le code de la procédure echanger où les trois lignes permettant la permutation des valeurs sont incomplètes.
Cette procédure echanger reçoit en paramètres :
-
une liste
lst, -
deux entiers
i1eti2représentant deux index de cases dans cette liste.
Cette procédure ne retourne rien (comme toute procédure) mais échange le contenu des cases correspondant aux index i1 et i2.
def echanger(lst: list, i1: int, i2: int) -> None:
a = ...................... # ligne 2
.......................... # ligne 3
.......................... # ligne 4
return None Proposer ci-dessous un code pour les lignes 2 à 4 permettant de compléter la procédure echanger précédente :
En utilisant la fonction get_position_min et la procédure echanger, proposer une procédure tri_selection qui correspond à l'algorithme de tri par sélection, c'est à dire qui prend comme paramètre une liste et qui
trie cette liste triée par ordre croissante par la méthode de tri par sélection et qui ne renvoie rien.
Pensez à vérifier la procédure écrite, par exemple avec la liste suivante : [1,8,6,4,3,9,20,7].
Pour visualiser comment cet algorithme trie une liste quelconque, accéder à un site Web en cliquant sur l'image ci-dessous :
Un fois accédé.e à ce site, cliquer sur Trier pour lancer l'application.


Voici ci-contre une animation qui permet de visualiser le tri par sélection :
-
les nombres sur fond jaune sont déjà triés,
-
le nombre sur fond rouge est le minimum de ceux déjà étudiés parmi les nombres encore à trier,
-
le nombre sur fond bleu est celui en cours d'étude (celui dont la valeur sera comparée au minimum actuel sur fond rouge),
-
la double flèche noire signifie qu'il y a permutation des valeurs ciblées.
Voici une visualisation de l'algorithme de tri par sélection avec une danse gitane :
Voici une liste de nombres à trier : [4, 9, 6, 7, 12, 3, 4].
Écrire la trace d'exécution de la fonction tri_selection précédente en faisant apparaître pour chaque valeur de i : la valeur de i, l'élément à classer, sa position initiale puis la liste déjà triée puis la liste totale une fois
la permutation avec le minimum effectuée.
Voici un exercice à faire en autonomie pour tester votre maîtrise sur
la recherche de l'indice du minimum d'une liste.
Cet exercice est issu du site collaboratif de la forge.
Complexité
Vous allez désormais calculer la complexité de l'algorithme de tri par sélection, rappelé ci-dessous, dans le pire des cas, c'est à dire dans le cas où toutes les valeurs sont triées dans l'ordre décroissant.
# Les deux fonctions étudiées précédemment :
# la fonction de recherche de l'index du minimum :
def positionner(lst: list, depart: int) -> int:
pos = depart # pos stocke la position du minimum : lst[pos] sera donc le minimum trouvé
i= pos+1
while i < len(lst):
if lst[i] < lst[pos]: # cas où une valeur plus petite que le minimum est trouvée
pos = i
i += 1
return pos # index du minimum de la liste entre depart et dernière valeur
# la procédure d'échange de deux termes :
def permuter(lst: list, i1: int, i2: int) -> None:
a = lst[i1] # utilisation d'une variable temporaire pour stocker la valeur qui sera écrasée par remplacement par la seconde valeur
lst[i1] = lst[i2]
lst[i2] = a
return None # aucun retour : la permutation a eu lieu sur la liste lst qui est donc modifiée.
# Tri par sélection
def tri_selection(lst: list) -> None:
for i in range(len(lst)-1): # on balaie toute la liste
pos = positionner(lst, depart=i) # on cherche le minimum parmi les termes non encore triés
if pos != i: # cas où le minimum n'est pas placé juste après la partie déjà triée
permuter(lst, i1=i, i2=pos)
return None # aucun retour : la permutation a eu lieu sur la liste lst qui est donc modifiée. On considère que :
-
chaque affectation correspond à une opération,
-
chaque comparaison correspond à une opération,
-
chaque obtention du terme d'une liste à partir de son index correspond à une opération.
QCM sur Socrative pour déterminer la complexité de la procédure de tri par sélection.
Vidéo de correction sur la complexité :Le coût du tri par sélection est quadratique dans le pire des cas, c'est-à-dire lorsque la liste est triée par ordre décroissant.
Il existe des tris plus rapides en temps que les deux tris vus dans ce cours. Vivement le cours de Terminale NSI pour en découvrir certains !
Exercices
Trouver des erreurs dans les codes suivants correspondant à des fonctions de tri par sélection puis les corriger.
Premier code
def tri_1(liste):
for i in range(len(liste)):
min = i
for j in range(i+1, len(liste)):
if liste[min] > liste[j]:
min = j
liste[i] = liste[min]
liste[min] = liste[i]
return liste Deuxième code
def tri_2(liste):
i = 0
while i < len(liste):
min = i
for j in range(i+1, len(liste)):
if liste[min] > liste[j]:
min = j
_temp = liste[i]
liste[i] = liste[min]
liste[min] = _temp
return liste Troisième code
def tri_3(liste):
i = 0
while i < len(liste):
min = i
for j in range(i+1, len(liste)):
if liste[min] > liste[j]:
min = j
_temp = liste[i]
liste[i] = liste[min]
liste[min] = _temp
i = i+1
return listeQuatrième code
def tri_4(liste):
for i in range(len(liste)):
min = i
j = min+1
while j < len(liste) and liste[min] > liste[j]:
min = j
j = j+1
_temp = liste[i]
liste[i] = liste[min]
liste[min] = _temp
i = i+1
return liste Adapter le programme de tri par sélection pour avoir une fonction tri_selection_decroissante renvoyant la liste entrée comme paramètres ordonnée par ordre décroissant.
Un des objectifs à maîtriser de ce chapitre est de savoir écrire seul.e les deux algorithmes de tri déjà vus.
-
Écrire, sans regarder le cours et les exercices précédents, l'algorithme de tri par insertion.
-
Écrire, sans regarder le cours et les exercices précédents, l'algorithme de tri par sélection.
-
Le tri par sélection est une méthode pour trier les valeurs d'un tableau (= liste en Python) par ordre croissant.
-
Pour une une liste de taille $n$, le tri par sélection consiste à répéter de l'indice (=position) $i=0$ jusqu'à celle $i=n-2$ (avant dernière valeur du tableau) les opération suivantes :
-
Repérer la position du minimum de la zone non triée :
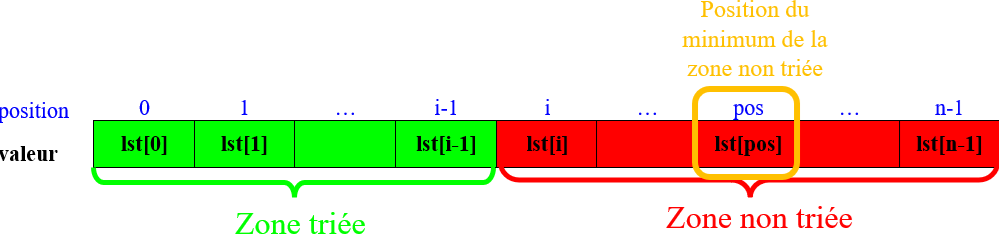
-
Si ce minimum est plus strictement plus petit que le premier élément de la zone non triée, alors permuter ces deux valeurs :

-
-
Une écriture du tri par sélection en Python est :
# la fonction de recherche de l'index du minimum : def positionner(lst: list, depart: int) -> int: pos = depart # pos stocke la position du minimum : lst[pos] sera donc le minimum trouvé i = pos+1 while i < len(lst): if lst[i] < lst[pos]: # cas où une valeur plus petite que le minimum est trouvée pos = i i += 1 return pos # index du minimum de la liste entre depart et dernière valeur # la procédure d'échange de deux termes : def permuter(lst: list, i1: int, i2: int) -> None: a = lst[i1] # utilisation d'une variable temporaire pour stocker la valeur qui sera écrasée par remplacement par la seconde valeur lst[i1] = lst[i2] lst[i2] = a return None # aucun retour : la permutation a eu lieu sur la liste lst qui est donc modifiée. # Tri par sélection def tri_selection(lst: list) -> None: for i in range(len(lst)-1): # on balaie toute la liste pos = positionner(lst, depart=i) # on cherche le minimum parmi les termes non encore triés if pos != i: # cas où le minimum n'est pas placé juste après la partie déjà triée permuter(lst, i1=i, i2=pos) return None # aucun retour : la permutation a eu lieu sur la liste lst qui est donc modifiée. -
Le coût en temps d'exécution du tri par sélection est quadratique dans le pire des cas et en moyenne.
Voici un exercice à faire en autonomie pour tester votre maîtrise sur
le tri par sélection.
Cet exercice est issu du site collaboratif de la forge.
Invariant
Intérêt
Il n'est pas évident de savoir si un algorithme fonctionne correctement dans tous les cas. Il se peut très bien que l'algorithme fonctionne dans les cas de test mais qu'il existe au moins un cas, non testé, où l'algorithme ne fonctionne pas.
Certains algorithmes peuvent semblaient au premier regard corrects et même fonctionner sur des premiers tests (cf. l'algorithme tri_3 de l'exercice 12 supra).
Comme un ne peut pas tester tous les cas possibles pour prouver qu'il n'existe aucun cas où l'algorithme dysfonctionne :
Comment être sûr que lorsqu'un algorithme renvoie un résultat, que ce résultat est forcément celui attendu ?
Il existe un moyen de démontrer (au sens mathématique du terme) la correction d'un algorithme : il suffit d'utiliser un invariant de boucle
Invariant de boucle
Pour un algorithme donné, un invariant de boucle, est une propriété qui, si elle est vraie avant l'exécution d'une itération de cette boucle, elle le demeure après l'exécution de l'itération de cette boucle.
Un outil d'une puissance ... !
Considérons d'abord un algorithme plus simple que les deux algorithmes de tri vu précédemment. Voici son écriture en langage courant :
1 Saisir une valeur pour n 2 p←1 3 Pour i allant de 1 à n faire 4 p←p*2 5 Fin_Pour 6 Afficher la valeur de p
-
Faire tourner à la main cet algorithme pour quelques valeurs de $n$ petites.
-
Pour une valeur de $n$ saisie quelconque, qu'affiche l'algorithme ?
Dans l'algorithme précédent, la boucle considérée est la boucle Pour commençant à la ligne 3.
Considérons la propriété suivante : après la $i^{\text{ème}}$ itération, $p=2^i$
Nous allons montrer que cette propriété est un invariant de la boucle Pour de algorithme précédent.
Pour cela, nous allons procéder en trois étapes :
-
INITIALISATION : Commencer à montrer que la propriété est vraie au début de la boucle, c'est à dire à la fin de la phase d'initialisation,
-
CONSERVATION : Finir par montrer que la propriété reste vraie après l'exécution d'une itération, c'est à dire, on va supposer que la propriété est vraie pour une valeur de $i$ donnée et montrer que la propriété est encore vraie pour la valeur suivante de $i$, qui peut être notée $i+1$.
-
TERMINAISON : Conclure quant à la correction de l'algorithme, une fois la boucle terminée.
Première étape : INITIALISATION
Avant le début de la boucle Pour, $p$ vaut 1 d'après la ligne 2 de l'algorithme.
Avant la première itération, la propriété $p=2^i$ est vraie car $2^0=1$.
Nous avons donc montré que la propriété est vraie avant la première itération.
Deuxième étape : CONSERVATION
On choisit de se placer à une itération quelconque $i$. Et on suppose que la propriété est vraie donc $p=2^{i}$.
On procède alors à l'itération.
On alors $p$ qui devient $2^{i}\times 2=2^{i+1}$. Après l'itération $i+1$ on a bien $p=2^{i+1}$.
Vous pouvez visualiser cette étape avec le tableau suivant :
| Valeur de $i$ | Valeur de $p$ |
|---|---|
| $i$ | $2^i$ |
| $i+1$ | $2×2^i=2^{i+1}$ |
Dernière étape : TERMINAISON :
La propriété $p=2^i$ est un invariant de la boucle Pour de algorithme précédent.
Ainsi, à la fin de la boucle for lorsque $i=n$, $p$ contient la valeur $2^n$ ; l'algorithme renverra donc bien la valeur de $2^n$.
Les étapes précédentes correspondent au raisonnement vu en terminale en spécialité mathématiques qui s'appelle un raisonnement par récurrence où la première étape s'appelle une initialisation et la seconde la phase d'hérédité.
Voici un script :
def mystere(k: int, p: int) -> int:
m = 1
i = 0
while m < p:
m = m*k
i += 1
return m -
Que renvoie la fonction
mystèreprécédente ? -
Proposer un invariant de la boucle
whilede cette fonction. -
Prouver que la propriété conjecturée à la question 2. est bien un invariant de boucle.
-
Écrire un algorithme utilisant une boucle Pour permettant de calculer la somme des valeurs d’une liste de nombres entiers
-
Proposer un invariant de la boucle Pour de cet algorithme.
-
Montrer que l'algorithme donnera toujours le résultat voulu en prouvant que la propriété conjecturée à la question 2. est bien un invariant de boucle.
Invariant du tri par insertion
On rappelle l'algorithme du tri par insertion écrit en langage Python vu dans la première partie :
def tri_insertion(lst: list) -> list:
for i in range(1, len(lst)):
elt = lst[i]
j = i
while elt < lst[j-1] and j > 0:
lst[j] = lst[j-1]
j -= 1
lst[j] = elt
return lstNous avons vu qu'il faut insérer dans une liste déjà triée le premier terme non trié. Dès lors, la liste lst est découpée en 2 parties :
-
la première partie qui contient les éléments déjà triés : ceux d'index 0 à $i-1$ (le $i$ correspond à la variable $i$ dans l'algorithme ci-dessus). Cette partie peut être notée
lst[:i], -
la seconde partie qui contient les éléments à trier : ceux d'index $i$ à $n-1$. Cette partie peut être notée
lst[i:].
À chaque itération, la première partie de la liste contenant les éléments déjà triés est augmentée d'un terme : celui lst[i]
placé correctement.
Au vu de cette première partie, l'invariant de boucle de la boucle for de ce tri est
"À l'issue de l'itération $i$, les termes d'index 0 à $i$ sont rangés par ordre croissant.".
On considère la propriété "À l'issue de l'itération $i$, les termes d'index 0 à $i$ sont rangés par ordre croissant."
-
Justifier que la propriété est vraie avant la première itération.
-
Considérons un entier $k$ compris entre 1 et $n-2$ tel que la propriété est vraie pour cet entier $k$, c'est à dire tel que les termes d'index 0 à $k$ sont rangés par ordre croissant. Montrer qu'à l'issue de l'itération suivante (celle où $i$ prend la valeur $k+1$), les termes d'index 0 à $k+1$ sont triés par ordre croissant.
-
Pourquoi est-on certain que, quelle que soit la liste proposée, la fonction
tri_insertionrenverra cette liste classée par ordre croissante ?
Invariant du tri par sélection
On rappelle ci-dessous l'algorithme du tri par sélection écrit en langage Python vu dans la seconde partie :
def tri_selection(lst):
for i in range(len(lst)-1):
min = i
for j in range(i+1, len(lst)):
if lst[min] > lst[j]:
min = j
lst[i], lst[min] = liste[min], lst[i]
return lstNous avons vu qu'il faut rajouter à une liste déjà triée le minimum des termes non triés. Dès lors, la liste lst est découpée en 2 parties :
-
la première partie qui contient les éléments déjà triés : ceux d'index 0 à $i-1$ (le $i$ correspond à la variable $i$ dans l'algorithme ci-dessus). Cette partie peut être notée
lst[:i], -
la seconde partie qui contient les éléments à trier : ceux d'index $i$ à $n-1$. Cette partie peut être notée
lst[i:].
-
Proposer une propriété qui pourrait être un invariant de boucle pour la première boucle
for. -
Justifier que la propriété est vraie initialement, c'est à dire pour $i=0$.
-
Considérons un entier $k$ compris entre 0 et $n-2$ tel que la propriété conjecturée à la question 1. est vraie pour cet entier $k$. Montrer qu'à l'issue de l'itération suivante (celle menant $i$ à $k+1$), cette propriété est encore vraie.
-
Pourquoi est-on certain que, quelle que soit la liste proposée, la fonction
tri_selectionrenverra cette liste classée par ordre croissante ?
-
Un invariant de boucle est une propriété qui est vraie :
-
avant le début de la boucle considérée,
-
reste vraie à chaque étape de la boucle.
-
-
Un invariant de boucle est encore vrai à la fin de la boucle.
-
Un invariant de boucle permet de prouver qu'à l'issue d'une boucle, on obtient bien un résultat recherché.
-
Un invariant de boucle pour le tri par insertion est la propriété : "À l'issue de l'itération $i$, les termes d'index 0 à $i$ sont rangés par ordre croissant".
-
Un invariant de boucle pour le tri par sélection est la propriété : "À l'issue de l'itération $i$, les termes d'index 0 à $i$ sont rangés par ordre croissant et tous les termes d'indice plus grand que $i$ sont plus grand ou égaux que le terme d'indice $i$".
Exercices de renforcement
Les corrections des exercices de cette partie (hormis le 20 pour lequel un lien direct est proposé) sont disponibles sur le jupyter disponible ici.
Voici une liste de nombres à trier : [9, 3, 5, 8, 1, 4, 5].
Écrire la trace d'exécution de la fonction tri_insertion vue au 1.2 en faisant apparaître les valeurs de $i$
et de $j$ considérées, l'élément à classer, la liste des éléments déjà triés et la liste complète
(en partie) triée.
Si la trace d'exécution reste délicate pour vous, cherchez l'exercice suivant afin que vous visualisiez mieux le tri par insertion.
Voici un tableau pouvant servir comme trace d'exécution :
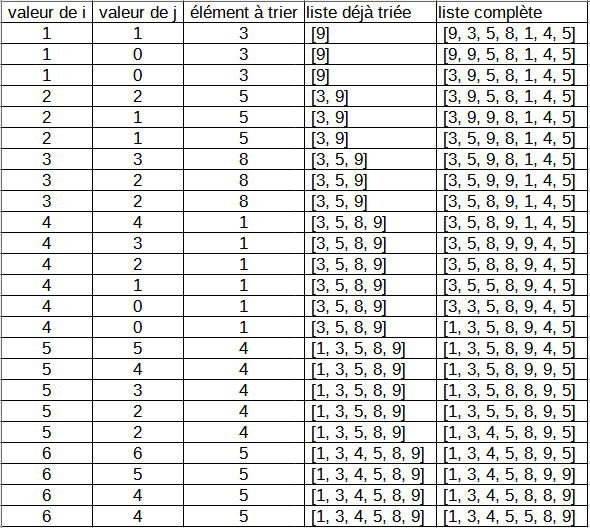
Pour faciliter la trace d'exécution, vous allez visualiser comment est modifiée étape par étape la liste [7,5,9,6,6,3] par le tri
par insertion vue au 1.2. Pour cela :
-
Sur une feuille, reproduisez (sans le texte explicatif) le schéma ci-dessous représentant les effets des instructions de la fonction
tri_insertionlors de la première itération oùi=1:
-
Complétez sur votre feuille le schéma afin de représenter similairement les itérations suivantes.
-
Explicitez quelle liste sera renvoyée par l'algorithme.
Vous pouvez vérifier votre travail à l'aide du corrigé en format pdf accessible par ce lien direct.
Que renvoie la fonction tri_insertion si vous donnez comme paramètres d'entrée la liste suivante :
lst = ['Belgique', 'Pologne', 'Suède', 'Allemagne', 'France', 'République Tchèque', 'Portugal']
On obtient comme résultat : ['Allemagne', 'Belgique', 'France', 'Pologne', 'Portugal', 'République Tchèque', 'Suède'].
Conclusion : la liste de noms des États rangés par ordre alphabétique.
Voici ci-dessous le code d'une fonction mystère
def mystere(tab, valeur):
"""
tab – liste d'entiers triée par ordre décroissant
valeur – entier
Sortie : …………………………………………………………………………………………………………………………………
"""
return [x for x in tab if x >= valeur] + [valeur] + [x for x in tab if x < valeur]
-
Que renvoie l'appel
mystere([10, 8, 3], 4)? -
Que renvoie l'appel
mystere([15, 11, 9, 8, 8, 6, 5, 3, 2, 2, 1],7)? -
Que renvoie l'appel
mystere([12, 9, 6, 5, 5, 5, 3, 2], 6)? -
Compléter la ligne "Sortie : ..."" de la documentation afin d'expliciter le rôle de la fonction mystere.
-
L'appel
mystere([10, 8, 3], 4)renvoie[10, 8, 4, 3]. -
L'appel
mystere([15, 11, 9, 8, 8, 6, 5, 3, 2, 2, 1], 7)renvoie[15, 11, 9, 8, 8, 7, 6, 5, 3, 2, 2, 1]. -
L'appel
mystere([12, 9, 6, 5, 5, 5, 3, 2], 6)renvoie[12, 9, 6, 6, 5, 5, 5, 3, 2]. -
Compréhension de la dernière ligne :
[x for x in tab if x >= valeur]signifie que l'on balaye toute la liste (de l'élément d'index 0 au dernier d'indexlen(tab); parmi ces éléments, on ne garde que les éléments supérieurs ou égaux àvaleur, sans modifier l'ordre.
Ainsi[x for x in tab if x >= valeur]sera la liste extraite detabcontenant tous les termes de la liste supérieurs ou égaux àvaleur, termes encore rangés par ordre décroissant.Ensuite,
+ [valeur]signifie que l'on ajoute à cette liste extraite l'élémentvaleurà la fin.Enfin
+ [x for x in tab if x >= valeur]signifie que l'on balaye toute la liste (de l'élément d'index 0 au dernier d'indexlen(tab); parmi ces éléments, on ne garde que les éléments strictement inférieurs àvaleur, sans modifier l'ordre et ces éléments sont ajoutés à la fin de la liste qui sera renvoyée.
Ainsi[x for x in tab if x >= valeur] + [valeur] + [x for x in tab if x > valeur]sera la liste où l'élémnetvaleura été inséré dans la listetabde sorte que tous les termes sont rangés par ordre décroissant.Réponse à la question posée :
Sortie : insère une valeur dans une liste classée de telle sorte que la liste augmentée est encore classée.
Compléments pour approfondir
Un autre tri
-
La vidéo suivante illustre cet autre tri entre la 54ème seconde et 3 minutes 56 secondes.
Regardez cette vidéo.
-
Proposez un algorithme en langage Python qui correspond au tri proposé par la vidéo.
Voici un exercice à faire en autonomie pour tester votre maîtrise sur
le tri à bulle.
Cet exercice est issu du site collaboratif de la forge.
Encore un autre tri : le tri rapide
Cet exercice est fortement inspiré d'un inspiré d'un exercice proposé par M. Vautrot lors de la formation au DIU EIL dispensée à l'université de Reims.
Voici le principe du tri rapide (ou quick-sort en anglais):
-
choisir une valeur pivot,
-
placer tous les éléments supérieurs à cette valeur pivot à droite de ce pivot,
-
placer tous les éléments inférieurs à cette valeur pivot à gauche de ce pivot,
-
appliquer cet algorithme sur la partie à droite du pivot et sur la partie à gauche du pivot si ces parties contiennent au moins deux valeurs.
Vous pouvez visualiser cet algorithme avec cette danse hongroise :
Voici ci-dessous un algorithme en langage naturel qui correspond à une partie tri rapide : celle qui permet de mettre
en oeuvre les 3 premières étapes du tri rapide. (La dernière étape nécessite la récursivité qui sera vue en terminale NSI).
On considère dans cet algorithme les notations suivantes :
-
ipivotcorrespond à l'index de la (ou d'une des) valeur(s) pivot(s).On choisit ici de prendre comme valeur pivot la première valeur de la liste que l'on traite.
-
idebcorrespond à l'index du premier élément de la liste extraite traitée. -
ifincorrespond à l'index du dernier élément de la liste extraite traitée.
1 initialiser ipivot à ideb
2 Tant que ideb < ifin faire #(tant qu'il reste des valeurs mal placées par rapport à la valeur pivot)
3 Tant que la valeur correspondant à ifin est plus grande strictement que la valeur du pivot faire
4 on décrémente ifin.
5 Fin Tant que #(ainsi ifin correspond soit à l'indice du pivot soit du premier terme rencontré par la droite qui est inférieur ou égal à la valeur du pivot)
6 Tant que la case correspondant à ideb est inférieure ou égale au pivot et ideb est plus petit que ifin faire
7 on incrémente ideb.
8 Fin Tant que #(ainsi ideb correspond soit à l'indice ifin soit du premier terme rencontré par la gauche qui est strictement supérieur à la valeur du pivot)
9 Si ideb < ifin alors #(cas où ideb correspond à l'index d'une valeur strictement supérieure à celle du pivot)
10 échanger la valeur d'indice ideb et la valeur d'indice ifin. #(Ainsi, la valeur trouvée strictement plus grand que le pivot est permutée soit avec une valeur inférieure ou égale à celle du pivot)
11 Fin si
12 Fin Tant que
13 Si ifin est différent de ipivot alors #(ideb et ifin indique la valeur la plus à droite inférieure ou égale à celle du pivot : on permute le pivot (premier élément de la liste) avec cette valeur)
14 échanger la valeur d'indice ipivot et la valeur d'indice ifin.
15 Fin si
Écrire une procédure partitionner_rapide qui prend en paramètres une liste liste et deux entiers ideb et
ifin et qui applique l'algorithme décrit ci-dessus.
Créer une fonction obtenir_liste qui prend en paramètre un nombre entier $n$ non nul et qui renvoie une liste de nombres entiers aléatoires entre 0 et 10
de taille $n$.
Penser à utiliser la fonction randint du module random.
Créer un script qui répète un grand nombre de fois la création d'une liste aléatoirement et teste sur celle-ci l'application de la procédure
partionner_rapide : sur la liste modifiée par cette procédure, le script doit vérifier que les valeurs inférieures au pivot sont à gauche et
celles supérieures au pivot sont à droite.
La procédure partitionner_rapide permet de savoir précisément la position que doit avoir la valeur du pivot dans la liste finale triée.
Pour obtenir un tri complet, il suffit de répéter l'action de cette fonction sur la partie à gauche de ifin (ifin exclu) et sur la partie
à droite de ifin (ifin exclu) si ces parties contiennent au moins 2 éléments.
Pour cela, la récursivité vue en Terminale sera utilisée.
Le fait que l'on connaisse la position finale de la valeur pivot et que l'on est découpée la liste en deux sous-listes plus petites à trier séparément permet faire partager la suite du procédé entre différents processeurs : on parle de parallélisation.
Comparaison de temps de calcul
On admet dans cette partie que l'algorithme de tri rapide peut s'écrire ainsi (les appels à elle-même de la procédure correspondent à la notion de récursivité) :
def tri_rapide(liste: list, ideb: int, ifin: int) -> None:
"""
Le premier argument de tri_rapide est la liste à triée.
Le tri_rapide s'appliquera sur l'ensemble des éléments dont l'index est compris entre ideb et ifn, inclus.
"""
_id = ideb
_if = ifin
while ideb < ifin:
while liste[ifin] > liste[_id]:
ifin -= 1
while liste[ideb] ≤ liste[_id] and ideb < ifin:
ideb += 1
if ideb < ifin:
_temp = liste[ideb]
liste[ideb] = liste[ifin]
liste[ifin] = _temp
if _id != ifin:
_temp = liste[ifin]
liste[ifin] = liste[_id]
liste[_id] = _temp
if ifin - _id > 1:
tri_rapide(liste, _id, ifin-1) # appel récursif sur la partie à gauche du pivot
if _if - ifin > 1:
tri_rapide(liste, ifin+1, _if) # appel récursif sur la partie à droite du pivot
return None
Nous avions vu dans le chapitre sur la complexité que l'on peut chronométrer le temps
d'exécution d'une fonction en utilisant le module timeit.
Celui-ci contient la méthode
import default_timer qui calcule le temps d’exécution relatif à une fonction donnée.
-
-
Créer aléatoirement une liste de 1000 nombres entiers compris entre 0 et 100.
-
Utiliser cette méthode
default_timerafin de mesurer le temps nécessaire à la procéduretri_rapidepour trier cette liste.
-
-
-
Créer aléatoirement une liste de 1000 nombres entiers compris entre 0 et 100.
-
Utiliser cette méthode
default_timerafin de mesurer le temps nécessaire à la procédure de tri par insertion pour trier cette liste. -
Comparer le temps mis par ces deux procédures pour trier une liste de même taille.
-
-
-
Créer aléatoirement une liste de 1000 nombres entiers compris entre 0 et 100.
-
Utiliser cette méthode
default_timerafin de mesurer le temps nécessaire à la procédure detri_rapidepour trier une copie de cette liste.Utiliser la méthode
copy. -
Mesurer le temps nécessaire à la procédure de tri par insertion pour trier une copie de la même liste.
-
Pareil pour le tri par sélection puis pour le tri à bulles
La comparaison précédente est en fait peu pertinente puisque le tri s'est opéré sur deux listes surement différentes sur lesquelles nous n'avons que peu de contrôles puisqu'elles ont été créée de manière aléatoire. En effet, une liste déjà presque triée par ordre croissant nécessite beaucoup moins d'opérations (donc de temps de calcul) à trier qu'une liste entièrement rangée par ordre décroissante (qui est le pire des cas à trier par ordre croissant).
Dès lors, chaque procédure de tri doit s'effectuer sur la même liste.
Comme ces procédures modifie la liste initiale, puisqu'elles la trient, il faut faire opérer chaque procédure de tri non pas sur la liste initiale mais sur une copie indépendante. -
-
Quitte à modifier la taille de la liste initiale et à répéter les mesures précédentes, déterminer quel semble être la procédure de tri qui semble être la plus rapide entre le tri par insertion, le tri par sélection, le tri à bulles et le tri rapide.
Afin de mieux visualiser la complexité de chacun des quatres tris, le programme suivant é été lancé. Il permet de créer une liste de 20 listes aléatoires dont la taille a été choisie puis tester le temps mis en moyenne par chacun des tris pour trier une copie de chacune des 20 listes.
from timeit import default_timer as timer
from random import randint
# définition de chacun des tris :
# tri par insertion
def tri_insertion(liste: list) -> None:
for i in range(1, len(liste)): # le premier élément forme seul une liste classée
elt = liste[i] # élément à classer
j = i
while elt < liste[j-1] and j > 0: # permutation avec le précédent s'il est plus grand
liste[j] = liste[j-1]
j -= 1
liste[j] = elt # placement au bon endroit
return None
# tri par sélection
def tri_selection(liste: list) -> None:
for i in range(1, len(liste)):
j = i
elmt = liste[i]
while j > 0 and liste[j-1] > elmt:
liste[j] = liste[j-1]
j -= 1
liste[j] = elmt
return None
# tri à bulles
def tri_bulle(liste: list) -> None:
i = 0
continuer = True
while i < len(liste) and continuer:
continuer = False
for j in range(len(liste) - i - 1):
if liste[j] > liste[j+1]:
_temp = liste[j]
liste[j] = liste[j+1]
liste[j+1] = _temp
continuer = True
return None
# tri rapide
def tri_rapide(liste: list, ideb: int, ifin: int) -> None:
"""
Le premier argument de tri_rapide est la liste à triée.
Le tri_rapide s'appliquera sur l'ensemble des éléments dont l'index est compris entre ideb et ifn, inclus.
"""
_id = ideb
_if = ifin
while ideb < ifin:
while liste[ifin] > liste[_id]:
ifin -= 1
while liste[ideb] <= liste[_id] and ideb < ifin:
ideb += 1
if ideb < ifin:
_temp= liste[ideb]
liste[ideb] = liste[ifin]
liste[ifin] = _temp
if _id!=ifin:
_temp= liste[ifin]
liste[ifin] = liste[_id]
liste[_id] = _temp
if ifin - _id > 1:
tri_rapide(liste, _id, ifin-1) # appel récursif sur la partie à gauche du pivot
if _if - ifin > 1:
tri_rapide(liste, ifin+1, _if) # appel récursif sur la partie à droite du pivot
return None
# création des listes sur lesquelles vont porter les tris
tab = []
for i in range(20):
tab.append([randint(0,100) for i in range(1000)])
# mesure des temps d'exécution
n= len(tab[1])
# cas du tri rapide
start = timer()
# tâches dont on veut mesurer le temps d'exécution.
for i in range(20):
tri_rapide(tab[i].copy(), 0, n-1)
end = timer()
print("temps moyen pour le tri rapide :", (end - start)/20) # affichage du temps écoulé
# cas du tri par insertion
start = timer()
# tâches dont on veut mesurer le temps d'exécution.
for i in range(20):
tri_insertion(tab[i].copy())
end = timer()
print("temps moyen pour le tri par insertion :", (end - start)/20) # affichage du temps écoulé
# cas du tri par sélection
start = timer()
# tâches dont on veut mesurer le temps d'exécution.
for i in range(20):
tri_selection(tab[i].copy())
end = timer()
print("temps moyen pour le tri par sélection :", (end - start)/20) # affichage du temps écoulé
# cas du tri à bulles
start = timer()
# tâches dont on veut mesurer le temps d'exécution.
for i in range(20):
tri_bulle(tab[i].copy())
end = timer()
print("temps moyen pour le tri à bulles :", (end - start)/20) # affichage du temps écoulé
Voici les différents temps moyens obtenus pour des listes respectivement de 100, 1000 et 10000 valeurs :
| nom du tri | listes de taille 100 | listes de taille 1000 | listes de taille 10000 |
|---|---|---|---|
| tri rapide | 0.00020841999999999806 | 0.005004499999999995 | 0.126142405 |
| tri par insertion | 0.0007595600000000035 | 0.08703027999999999 | 5.560711530000001 |
| tri par sélection | 0.0008007900000000012 | 0.09540426499999999 | 5.48470522 |
| tri à bulles | 0.0018068850000000024 | 0.23651464 | 12.932365125 |
-
Parmi les 4 tris étudiés lesquels semblent bien avoir une complexité quadratique ? Expliquer comment vous utiliser le tableau précédent.
-
Celui ou ceux qui ne semblent pas avoir une complexité quadratique, a-t-il ou ont-ils une complexité linéaire ?
-
Celui ou ceux qui ne semblent pas avoir une complexité quadratique, a-t-il ou ont-ils une complexité intermédiaire entre linéaire et quadratique ?
QCM
Questions issues de la Banque Nationale de Sujets
Propriétaire des ressources ci-dessous : ministère de l'Éducation nationale et de la jeunesse, licence CC BY SA NC
Voici une sélection de questions issues de la banque nationale de sujets, répondez à ces questions (attention, cette sélection n'est pas exhaustive).
L'algorithme suivant permet de calculer la somme des N premiers entiers, où N est un nombre entier donné :
i = 0
somme = 0
while i < N :
i = i +1
somme = somme + i Un invariant de boucle de cet algorithme est le suivant :
Réponses :
A- somme = 0 + 1 + 2 + ... + i et i < N
B- somme = 0 + 1 + 2 + ... + N et i < N
C- somme = 0 + 1 + 2 + ... + i et i < N+1
D- somme = 0 + 1 + 2 + ... + N et i < N+1
Soit $T$ le temps nécessaire pour trier, à l'aide de l'algorithme du tri par insertion, une liste de 1000 nombres entiers. Quel est l'ordre de grandeur du temps nécessaire, avec le même algorithme, pour trier une liste de 10 000 entiers, c'est-à-dire une liste dix fois plus grande ?
Réponses :
A- à peu près le même temps $T$
B- environ $10 \times T$
C- environ $100 \times T$
D- environ $T^2$
Pour trier par sélection une liste de 2500 entiers, le nombre de comparaisons nécessaires à l’algorithme est de l’ordre de :
Réponses :
A- $\sqrt{2500}$
B- $2500$
C- $2500^2$
D- $2^{2500}$
Combien d’échanges effectue la fonction Python suivante pour trier un tableau de 10 éléments au pire des cas ?
def tri (tab):
for i in range (1, len(tab)):
for j in range (len(tab) - i):
if tab[j] > tab[j+1]:
tab[j], tab[j+1] = tab[j+1], tab[j]
Réponses :
A- $10$
B- $45$
C- $55$
D- $100$
Un algorithme de tri d’une liste d’entiers est implémenté de la façon suivante :
def trier(L):
for i in range(len(L)):
indice_min = i
for j in range(i+1, len(L)):
if L[j] < L[indice_min]:
indice_min = j
L[i], L[indice_min] = L[indice_min], L[i]
# assertion vraie à cet endroit
return L Parmi les assertions suivantes laquelle reste vraie à chaque itération de la boucle, à l'endroit indiqué ci-dessus ?
Réponses :
A- la sous-liste L[0:i+1] contient les i plus grandes valeurs de L triées par ordre décroissant
B- la sous-liste L[0:i+1] contient les i plus grandes valeurs de L triées par ordre croissant
C- la sous-liste L[0:i+1] contient les i plus petites valeurs de L triées par ordre décroissant
D- la sous-liste L[0:i+1] contient les i plus petites valeurs de L triées par ordre croissant
Autres QCM
Les deux QCM suivants sont issus de https://genumsi.inria.fr.
On souhaite écrire une fonction tri_selection(t), qui trie le tableau t dans l'ordre croissant : parmi les 4 programmes suivants, lequel est correct ?
Réponses :
A-
def tri_selection(t) :
for i in range (len(t)-1) :
min = i
for j in range(i+1, len(t)):
if t[j] < t[min]:
min = j
tmp = t[i]
t[i] = t[min]
t[min] = tmp B-
def tri_selection(t) :
for i in range (len(t)-1) :
min = i
for j in range(i+1, len(t)-1):
if t[j] < t[min]:
min = j
tmp = t[i]
t[i] = t[min]
t[min] = tmpC-
def tri_selection(t) :
for i in range (len(t)-1) :
min = i
for j in range(i+1, len(t)):
if t[j] < min:
min = j
tmp = t[i]
t[i] = t[min]
t[min] = tmp D-
def tri_selection(t) :
for i in range (len(t)-1) :
min = i
for j in range(i+1, len(t)):
if t[j] < t[min]:
min = j
tmp = t[i]
t[min] = t[i]
t[i] = tmp
On considère un algorithme de tri par sélection, dans lequel la fonction :
echanger(tab[i], tab[j]) effectue l'échange des $i$ème et $j$ième valeurs du tableau
tab.
nom: tri_sélection
paramètre: tab, tableau de n entiers, n>=2
Traitement:
pour i allant de 1 à n-1:
pour j allant de i+1 à n:
si tab[j] < tab[i]:
echanger(tab[i], tab[j])
renvoyer tab Quel est l'invariant de boucle qui correspond précisément à cet algorithme ?
Réponses :
A- Tous les éléments d'indice supérieur ou égal à i sont triés par ordre croissant
B- Tous les éléments d'indice compris entre 0 et i sont triés par ordre croissant et les éléments d'indice supérieurs ou égal à i leurs sont tous supérieurs
C- Tous les éléments d'indice supérieur ou égal à i sont non triés
D- Tous les éléments d'indice compris entre 0 et i sont triés, on ne peut rien dire sur les éléments d'indice supérieur ou égal à i
Générateur aléatoire de questions sur ce chapitre
Il faut actualiser la page pour changer de question. Propriétaire de la ressource : le site GeNumsi en licence CC BY_NC-SA
Sitographie
Voici une liste de sites traitant des tris :
Savoir faire et Savoir
- Écrire un algorithme de tri par insertion.
- Écrire un algorithme de recherche d'un minimum dans une liste
- Écrire un algorithme de tri par sélection.
- Déterminer la complexité d'un algorithme de tri.
- Définir un invariant de boucle lors d'un algorithme de tri par insertion ou par sélection.
- permutation de deux termes d'une liste
- invariant de boucle
- Complexité quadratique

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International