-
DC1 : tableau (= liste en Python)
-
A2 : complexité
Recherche dans une liste, l'algorithme naïf
Pour trouver un nombre dans une liste il suffit de balayer la liste et de renvoyer True
dès qu’on trouve l’élément recherché et False si on a parcouru toute la liste sans trouver
l’élément.
//déclarations val: Valeur cherchée (entier) i: Entier liste : liste de N entiers triés retour : Booléen //initialisation retour ← faux i ← 0 //Boucle de recherche // La condition début inférieur ou égal à fin permet d'éviter de faire // une boucle infinie si 'val' n'existe pas dans le tableau. Tant que i < N et retour est faux: si liste[i] == val: retour ← vrai i ← i+1 //Affichage du résultat Si retour == vrai: Afficher "La valeur ", val, " est dans la liste." Sinon: Afficher "La valeur ", val, " n'est pas dans la liste."
Le but est d'implémenter la recherche naïve précédente en Python de manière itérative.
Pour cela écrire le script de la fonction naive_search(lst, val) où lst
est une liste d'entier et val la valeur à chercher dans la liste.
Cette fonction renvoie True si val est dans la liste lst
et False sinon.
Penser à tester cette fonction avec les valeurs 3, 12, 48 et
4 et avec la liste : ma_liste = [3, 5, 12, 15, 48]
Faire le même exercice en utilisant désormais une boucle for.
On voit que cet algorithme n'est peut-être pas le plus pertinent, car dans le pire des cas, c'est-à-dire le cas où l'élément cherché n'est pas présent, on devra parcourir toute la liste. Le coût en temps dans le pire des cas est donc linéaire.
La dichotomie : généralités
Cette méthode, vous la connaissez tous!
Vous avez probablement joué au jeu : trouve un nombre entre 1 et 100.
Vous avez commencé par proposer 50.
Si on vous répond, c'est plus, vous proposez 75 puis si l'on vous répond c'est moins vous proposez 62...
Vous êtes alors en train d'effectuer une recherche dichotomique !
Faire une recherche dichotomique, c'est chercher une valeur dans un tableau trié en prenant, à chaque étape, le milieu de l'ensemble des valeurs possibles pour éliminer la moitié des possibilités.
Méthode et exemple pas à pas
Soit une liste de $n$ objets déjà triés. On recherche un objet en particulier.
-
on choisit dans la liste l'objet médian (une moitié des objets est avant, l'autre moitié est après).
-
on compare les deux objets
Trois cas :
-
si on a trouvé l'objet cherché alors c'est fini.
-
si l'objet recherché est placé avant l'objet médian alors on recommence avec cette première partie de la liste.
-
si l'objet recherché est placé après l'objet médian alors on recommence avec cette seconde partie de la liste.
-
-
on répète cette démarche jusqu'à ce qu'au bout d'un certain nombre d'essais (cela se calcule) :
-
soit on a trouvé l'objet cherché,
-
soit il n'est pas dans la liste.
-
Prenons par exemple la liste triée suivante :
[1, 3, 4, 6, 7, 8, 10, 13, 14], où nous allons rechercher par dichotomie
l'élément 4.
On utilise deux pointeurs indice_gauche et indice_droit
pour délimiter la sous-liste sur laquelle porte la recherche courante, au départ il
s'agit de la liste entière.
indice_gauche pointe vers l'élément d'indice 0 et indice_droit pointe vers le dernier élément de notre liste qui ici a l'indice 8.
On cherche l'indice indice_centre de l'élément médian en ne gardant que la
partie entière de la moyenne indice_gauche et indice_droit,
ici $\frac{0+8}{2}=4$, l'élément médian est donc l'élément d'indice 4,
c'est-à-dire l'élément 7.
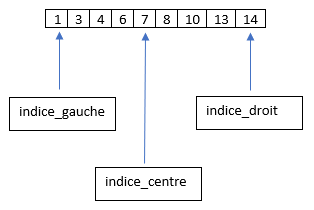
Maintenant on compare l'élément central 7 à l'élément recherché 4 : ici $4<7$, cela signifie que 4 ce trouve dans la première moitié de la liste (celle avant 7).
On modifie alors la valeur du pointeur indice_droit, qui prend la valeur de
(indice_centre-1), et on recommence avec cette nouvelle sous-liste.
indice_gauche = 0 ; indice_droit= 3 et indice_centre=1
(partie entière de $\frac{0+3}{2}$, c'est-à-dire de 1.5).
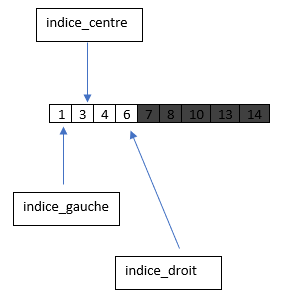
Maintenant on compare l'élément central 3 à l'élément recherché 4 : ici $4 > 3$, cela signifie que que 4 ce trouve dans la deuxième moitié de la sous-liste (celle après 3).
On modifie alors la valeur du pointeur indice_gauche, qui prend la valeur de
(indice_centre+1), et on recommence avec cette nouvelle sous-liste.
indice_gauche=2 ; indice_droit= 3 et indice_centre=2
(partie entière de $\frac{2+3}{2}$, c'est-à-dire de 2.5).
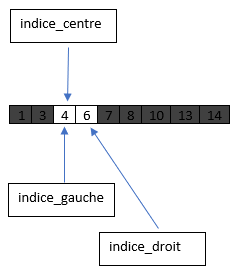
Maintenant on compare l'élément central 4 à l'élément recherché 4 : ici $4 = 4$, l'élément recherché est présent.
On reprend le tableau trié par ordre croissant de l'exemple précédent où l'on cherche la valeur 4.
Si la sous-liste devient vide, c'est-à-dire que le pointeur indice_gauche
devient supérieur au pointeur indice_droit, la recherche est infructueuse
et l'algorithme s'arrête.
-
Décrivez chacune des étapes de progression de la recherche dichotomique de l'élément 35 appliquée à la liste ordonnée
[2, 12, 17, 25, 33, 35, 44, 54, 77, 91].
Indiquez ensuite le nombre de comparaisons nécessaires à cette recherche. -
Décrivez chacune des étapes de progression de la recherche dichotomique de l'élément 50 appliquée à la liste ordonnée
[2, 12, 17, 25, 33, 35, 44, 54, 77, 91].
Indiquez ensuite le nombre de comparaisons nécessaires à cette recherche.
L'algorithme
Voici le pseudo-code en langage naturel de cet algorithme :
//déclarations indice_gauche, indice_droite, elmt, indice_centre: Entiers liste : liste de N entiers triés retour : Booléen (elmt est la valeur cherchée) //initialisation indice_gauche ← 0 indice_droite ← N-1 retour ← faux //Boucle de recherche // La condition début inférieur ou égal à fin permet d'éviter de faire // une boucle infinie si 'elmt' n'existe pas dans le tableau. Tant que retour != vrai et indice_gauche <= indice_droite: indice_centre ← partie_entière((indice_gauche + indice_droite)/2) si liste[indice_centre] == elmt: retour ← vrai sinon: si elmt > liste[indice_centre]: indice_gauche ← indice_centre+1 sinon: indice_droit ← indice_centre-1 //Affichage du résultat Si retour == vrai: Afficher "La valeur ", elmt, " est au rang ", indice_centre Sinon: Afficher "La valeur ", elmt, " n'est pas dans le tableau."
Voici une animation (inspirée de celle de www.infoforall.fr) qui permet de trier par dichotomie un tableau trié par ordre croissant :
Sélectionner la valeur cherchée dans le tableau :
| Indice | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Élément | 6 | 8 | 9 | 13 | 18 | 35 | 37 | 59 | 60 | 62 | 63 | 68 | 70 | 78 | 80 | 83 | 84 | 89 | 91 | 96 |
-
Écrire une fonction
recherche_dichotomiequi reçoit en paramètre une liste nomméelisteet l'élément recherché nomméelmtet qui retourne un booléen en fonction de la présence ou non de l'élément recherché. -
Tester le script avec les deux exemples traités dans l'exercice 3 (cf. accès direct.).
Voici une liste de prénom d'ami.e.s :
liste_amis = ['Ariel', 'Benjamin', 'Amir', 'Melvina', 'Hector', 'Zoé', 'Yasmine', 'Ursula', 'Andréa', 'Marie-Claire', 'Marc-Aurèle', 'Jim', 'Paula'
'Pietro', 'Xavier', 'Éléonore', 'Arthur', 'Firmin', 'Alice', 'Bob', 'Firdaous', 'Olga', 'Shinzo', 'Li', 'Mathéo', 'Rachel', 'Philippine', 'Tao'].
-
Trier par ordre croissant cette liste
liste_amis.Vous pouvez soit implémenter un tri par sélection ou par insertion pour vérifier que vous maîtrisez toujours les algorithmes vu au chapitre A3, soit vous pouvez utiliser directement la fonction
sorted:
lst2 = sorted(lst1):lst2est une liste triée formé des éléments de la listelst1. -
Utilisez votre programme de l'exercice 4 afin de savoir si
'Paulo'fait partie de la listeliste_amis. -
Utilisez votre programme de l'exercice 4 afin de savoir si
'Yasmine'fait partie de la listeliste_amis.
Le but de l'exercice est de compléter une fonction rechercher qui détermine
si une valeur val est présente
dans un tableau de valeurs tab triées dans l'ordre croissant.
L'algorithme traite le cas du tableau vide et il est écrit pour que la recherche dichotomique
ne se fasse que dans le cas où la valeur est comprise entre les valeurs extrêmes du
tableau.
def rechercher(tab, val):
"""
tab : tableau trié dans l'ordre croissant
val : nombre entier
La fonction renvoie True si tab contient val et False sinon
"""
# cas du tableau vide
if ...:
return False
# cas où val n'est pas compris entre les valeurs extrêmes
if (val < tab[...]) or ...:
return ...
# cas où val est compris entre les valeurs extrêmes
deb = 0
fin = ...
while deb <= fin:
mil = ...
if val == tab[mil]:
return ...
elif val > tab[mil]:
deb = ...
else:
fin = ...
return ...Compléter le script précédent puis tester avec le jeu de tests suivant :
assert rechercher([], 0) == False
assert rechercher([0, 1, 2, 3, 4, 5, 6, 7], 9) == False
assert rechercher([0, 1, 2, 3, 5, 6, 7], 4) == False
assert rechercher([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], 6) == True
Voici un exercice à faire en autonomie pour tester votre maîtrise de
l'algorithme de dichotomie.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
N'hésitez pas à basculer si la version à trous à compléter si besoin.
Voici un exercice à faire en autonomie pour tester votre maîtrise de
l'algorithme de dichotomie.
Il est similaire à l'exercice précédent, sauf qu'il n'y a plus de versions à trous
et que vous devez renvoyer le premier indice trouvé lorsqu'une valeur est
présente dans le tableau considéré.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Si la dernière ligne raise ValueError("La valeur cible n'est pas dans le tableau") vous gêne, n'y touchez pas
et faîtes comme si c'était un return "La valeur cible n'est pas dans le tableau"
dans le cas où la valeur cherchée n'est pas le tableau.
Complexité
Nous avons vu précédemment que l'algorithme naïf de recherche d'un nombre dans une liste triée
avait dans le pire des cas une complexité linéaire.
Voyons si la dichotomie est plus avantageuse de ce point de vu.
Déterminez le nombre maximal de comparaisons nécessaires à la recherche d'un élément dans une liste, en complétant le tableau ci-dessous.
| Taille de la liste | 0 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | N |
|---|---|---|---|---|---|---|---|---|---|---|
| Recherche séquentielle | ||||||||||
| Recherche dichotomique |
Le coût pour rechercher par la méthode par dichotomie une valeur dans un tableau à $2^n$
éléments est de l'ordre de $n$ dans le pire des cas.
On dit que le coût est logarithmique car le nombre $p$ tel que $2^p=N$
se note $log_2(N)=p$ ; $p$ est appelé logarithme de base 2 de $p$.
Cette fonction $log_2$ peut être définie quand $N$ est une puissance de $2$ par le programme suivant :
def log2(n):
compteur = 0
while n > 0:
compteur += 1
n = n // 2
return compteurExercice qui reprend le jeu introductif.
Écrire un programme qui permette à l'ordinateur de jouer contre l'utilisateur pour
retrouver un nombre.
L'utilisateur choisira un nombre entre 0 et 100 et l'ordinateur devra le trouver,
le plus efficacement possible.
À chaque proposition faite par l'ordinateur,
l'utilisateur devra donner une réponse sous la forme d'une chaîne de caractères codant
explicitement les notions de "plus grand", "plus petit" ou "bravo, tu as trouvé !".
Copier puis compléter le script suivant en vous servant des commentaires.
def ...:
print("Choisissez dans votre tête un nombre entre 0 et 100 et l'ordinateur essaiera de le deviner.")
print("Donnez-lui des indices en répondant par :")
print("'plus grand' ou plus simplement par '+' si le nombre choisi est plus grand que la proposition.")
print("'plus petit' ou plus simplement par '-' si le nombre choisi est plus petit que la proposition.")
print("'bravo, tu as trouvé !' ou plus simplement par'=' lorsque l'ordinateur trouve le bon nombre.")
bas = 0
haut = 100
trouve = ... # booléen
nb_essai = ... # entier
while ...:
# Proposition de l'ordinateur (entier au milieu de l'intervalle de recherche)
proposition = ...
print("L'ordinateur propose : ", ...)
nb_essai = ...
# L'utilisateur donne un indice
reponse = input("Réponse (plus grand ou + / plus petit ou - / bravo, tu as trouvé ! ou =) : ")
# Traitement de la réponse
if reponse == "plus grand" or reponse == "+":
...
elif reponse == "plus petit" or reponse == "-":
...
elif reponse == "bravo, tu as trouvé !" or reponse == "=":
trouve = ...
print("L'ordinateur a trouvé le nombre en", ..., "essai(s) !")
else:
print("Réponse non reconnue, merci d'utiliser : 'plus grand', '+', 'plus petit', '-', 'bravo, tu as trouvé !' ou '='.")Attention ! Il y a d'autres manières d'écrire le script demandé, manières tout aussi pertinentes que celle proposée ci-dessus avec des trous.
Voici un exercice à trous à faire en autonomie pour tester votre maîtrise de
l'algorithme de dichotomie et comprendre dans une application sur les listes
sont efficacité en terme de coût.
Cet exercice est issu du site collaboratif de la forge.
Variant de boucle
def recherche_dichotomie(lst, elt):
indice_gauche = 0
indice_droit = len(lst) - 1
rep = False
while rep == False and indice_gauche <= indice_droit :
indice_centre = (indice_gauche + indice_droit)//2
if lst[indice_centre] == elt :
rep = True
else:
if elt > lst[indice_centre]:
indice_gauche = indice_centre + 1
else:
indice_droit = indice_centre - 1
return repDans l'algorithme précédent, nous avons une boucle conditionnelle while, nous devons donc nous interroger sur la
terminaison de cet algorithme, c'est-à-dire le fait que l'algorithme se termine toujours
en un nombre fini d'étapes.
On appelle variant de boucle une quantité qui vérifie les trois conditions ci-dessous :
-
elle est toujours un nombre entier,
-
elle est positive ou nulle lorsque l'on reste dans la boucle,
-
elle décroît strictement à chaque itération de la boucle.
Un variant de boucle sert à prouver la terminaison d'une boucle, c'est-à-dire que l’on sort nécessairement de la boucle au bout d’un nombre fini d’itérations.
La variable longueur = indice_droit - indice_gauche est un variant de boucle pour l'algorithme de dichotomie.
Voici une démonstration à lire et à comprendre justifiant que longueur = indice_droit - indice_gauche est un variant de boucle.
Il suffit de prouver deux choses par définition du variant :
-
longueurest toujours positif ou nul. -
longueurdiminue strictement à chaque étape.
Première condition : longueur positive ou nulle :
La deuxième condition nécessaire de la boucle while : indice_gauche <= indice_droit signifie qu'à chaque itération
longueur est positif ou nul.
Seconde condition : longueur diminue strictement à chaque itération :
Étudions les étapes de chaque itérations :
-
L'itération commence par l'indice du milieu avec
indice_centre = (indice_gauche + indice_droit) // 2.
Forcémentindice_gauche <= indice_centre <=indice_droit -
Ensuite, l'itération se poursuit par une structure conditionnelle pour laquelle il y a trois cas :
-
Cas où
lst[indice_centre] == elt:La valeur cherchée est trouvée, le booléen
reppasse àTruece qui met fin à la bouclewhile. La terminaison est assurée alors. -
Cas où
lst[indice_centre] < elt:Alors
indice_gaucheprend la valeurindice_centre + 1si bien que la variablelongueurva diminuer au moins de 1. En effet :La nouvelle valeur de
longueurest :longueur = indice_droit - indice_gauche = indice_droit - (indice_centre + 1) = indice_droit - indice_centre - 1.
Commeindice_gauche <= indice_centre,indice_droit - indice_centre - 1 <= indice_droit - indice_gauche - 1.
Ainsi,longueur <= indice_droit - indice_gauche - 1: le variable a strictement diminuée. -
Cas où
lst[indice_centre] > elt:Alors
indice_droitprend la valeurindice_centre - 1si bien que la variablelongueurva diminuer au moins de 1. En effet :La nouvelle valeur de
longueurest :longueur = indice_droit - indice_gauche = (indice_centre - 1) - indice_gauche = indice_centre - indice_gauche - 1.
Commeindice_centre <= indice_droit,indice_centre - indice_gauche - 1 <= indice_droit - indice_gauche - 1.
Ainsi,longueur <= indice_droit - indice_gauche - 1: le variable a strictement diminuée.
-
Le variant diminuant strictement, il y a aura au plus $n+1$ itérations où $n$ est la valeur initiale du variant : l'algorithme se termine donc dans tous les cas !
On considère l'algorithme suivant :
def recherche(lst, elt):
pos = 0
n = len(lst)
while pos < n and lst[pos] != elt:
pos = pos + 1
return pos < n-
Dans quel cas la fonction
rechercherenvoieFalse? -
Démontrer que la variable définie par
var = n - posest un variant.
Voici une fonction separer qui prend en paramètre une liste lst
formée de nombres entiers et une valeur entière val.
Cette fonction est dite à effet de bord : elle modifie la liste
saisie comme argument et renvoie cette liste modifiée.
def separer(lst: list, val: int) -> list:
i = 0
j = len(lst) - 1
while i < j :
if lst[i] <= val:
i = i + 1
else:
temp = lst[i]
lst[i] = lst[j]
lst[j] = temp
j = j - 1
return lst-
Prouver que cette fonction se termine toujours en exhibant un variant de boucle.
-
Tester cette fonction avec les couples suivant :
-
[6, 8, 3, 9, 4, 1, 2, 6], 5 -
[6, 8, 3, 9, 4, 1, 2, 6], 4 -
[6, 8, 3, 9, 4, 1, 2, 6], 0 -
[6, 8, 3, 9, 4, 1, 2, 6], 9
-
-
Quel est le rôle des trois premières lignes suivant le
else:? -
Décrire le rôle de la fonction
separer.
Exercice ludique
Vous trouverez sur ce site d'un collègue de NSI un jeu de type "space invader" où il vous faudra utiliser judicieusement le principe de l'algorithme de dichotomie pour empêcher l'invasion de la Terre.
QCM
Questions issues de la Banque Nationale de Sujets
Propriétaire des ressources ci-dessous : ministère de l'Éducation nationale et de la jeunesse, licence CC BY SA NC
Voici une sélection de questions issues de la banque nationale de sujets, répondez à ces questions (attention, cette sélection n'est pas exhaustive).
Un algorithme de recherche dichotomique dans une liste triée de taille $n$ nécessite, dans le pire des cas, exactement $k$
comparaisons.
Combien cet algorithme va-t-il utiliser, dans le pire des cas, de comparaisons sur une liste de taille $2n$ ?
Réponses :
A- $k$
B- $k+1$
C- $2k$
D- $2k+1$
On considère la fonction suivante :
def f(x,L):
g = 0
d = len(L)-1
while g < d:
m = (g+d)//2
if x <= L[m]:
d = m
else:
g = m + 1
return gCette fonction implémente :
Réponses :
A- le tri par insertion
B- le tri par sélection
C- la recherche dichotomique
D- la recherche du plus proche voisin
En utilisant une recherche dichotomique, combien faut-il de comparaisons pour trouver une valeur dans un tableau trié de 1000 nombres ?
Réponses :
A- 3
B- 10
C- 1000
D- 1024
Quelle précondition suppose l'algorithme de recherche dichotomique dans un tableau ?
Réponses :
A- que le tableau soit à éléments positifs
B- que le tableau soit trié
C- que l'élément cherché dans le tableau soit positif
D- que l'élément cherché figure effectivement dans le tableau
La fonction ci-dessous permet d’effectuer une recherche par dichotomie de l’index
m de l’élément x dans un tableau L de valeurs distinctes et triées.
def dicho(x,L):
g = 0
d = len(L)-1
while g <= d:
m = (g+d)//2
if L[m] == x:
return m
elif L[m] < x:
g = m+1
else:
d = m-1
return None
Combien de fois la cinquième ligne du code de la fonction m = (g+d)//2 sera-t-elle exécutée dans l'appel
dicho(32, [4, 5, 7, 25, 32, 50, 51, 60]) ?
Réponses :
A- 1 fois
B- 2 fois
C- 3 fois
D- 4 fois
Autres QCM
Plusieurs des QCM suivants sont issus de https://genumsi.inria.fr.
Auteur : Christophe JOUBERT
Avec un algorithme de recherche dichotomique, combien d'étapes sont nécessaires pour déterminer que 45 n'est pas présent dans la liste suivante :
[1, 7, 12, 16, 18, 20, 24, 28, 35, 43, 69] ?
Réponses :
A- 2
B- 3
C- 4
D- 5
Autrice : Sylvie Genre
On souhaite écrire une fonction recherche_dichotomique(t, v), qui renvoie une position
de la valeur v
dans le tableau t, supposé trié, et None si v ne s'y trouve pas.
Parmi les 4 fonctions ci-dessous, laquelle est correcte ?
Réponses :
A-
def recherche_dichotomique(t, v) :
g = 0
d = len(t) - 1
while g <= d :
m = (g + d) // 2
if t[m] < v :
g = m + 1
elif t[m] > v :
d = m - 1
else :
return m
return NoneB-
def recherche_dichotomique(t, v) :
g = 0
d = len(t) - 1
while g <= d :
m = (g + d) // 2
if t[m] > v :
g = m + 1
elif t[m] < v :
d = m - 1
else :
return m
return NoneC-
def recherche_dichotomique(t, v) :
g = 0
d = len(t)
while g <= d :
m = (g + d) // 2
if t[m] < v :
g = m + 1
elif t[m] > v :
d = m - 1
else :
return m
return NoneD-
def recherche_dichotomique(t, v) :
g = 0
d = len(t) - 1
while g < d :
m = (g + d) // 2
if t[m] < v :
g = m + 1
elif t[m] > v :
d = m - 1
else :
return m
return NoneAuteur : Antony OLIVIER
Par quel moyen usuel peut-on démontrer la terminaison d'une boucle ?
Réponses :
A- une assertion
B- un invariant
C- un variant
D- la complexité
Dans la fonction suivante, les valeurs des variables x et y sont des entiers naturels :
def f(x, y) :
s = x
t = y
while t > 0 :
s = s + 1
t = t - 1
return sQuelle affirmation est fausse ?
Réponses :
A- La propriété s + t = x + y est un invariant de boucle.
B- La variable s + t est un variant de boucle.
C- La propriété t est supérieur ou égal à 0 est un invariant de la boucle while.
D- La variable t est un variant de la boucle while.
Générateur aléatoire de questions sur ce chapitre
Il faut actualiser la page pour changer de question. Propriétaire de la ressource : le site GeNumsi en licence CC BY_NC-SA
Sitographie
Voici une liste de sites traitant de la dichotomie :
Savoir faire et Savoir
- Savoir écrire la trace d'exécution d'un algorithme de dichotomie.
- Savoir écrire un algorithme de dichotomie.
- Savoir montrer la terminaison de la recherche dichotomique à l’aide d’un variant de boucle.
- Savoir la notion de complexité logarithmique.
- Savoir que le coût d'un algorithme de dichotomie est logarithmique.
- Savoir la notion de terminaison d'un algorithme.
- Savoir la notion de variant de boucle.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International