L’écriture sur des exemples simples de plusieurs implémentations d’une même structure de données permet de faire émerger les notions d’interface et d’implémentation, ou encore de structure de données abstraite.
- Contenus : Structures de données, interface et implémentation.
- Capacités attendus: Spécifier une structure de données par son interface. Distinguer interface et implémentation. Écrire plusieurs implémentations d’une même structure de données.
- Commentaires : L’abstraction des structures de données est introduite après plusieurs implémentations d’une structure simple comme la file (avec un tableau ou avec deux piles).
Dans ce cours nous allons aborder la notion de structure de données abstraite.
Nous allons à travers des exemples voir ce qu'est l'interface d'une structure de données. Nous allons par la suite implémenter ces structures en Python.
Interface d'une structure de données abstraite
Structure de données abstraite
Un type abstrait ou une structure de données abstraite est une spécification mathématique (c'est-à-dire la désignation précise) d'un ensemble de données et de l'ensemble des opérateurs associés à cet ensemble.
On qualifie d'abstrait ce type de données car il correspond à un cahier des charges qu’une structure de données doit ensuite implémenter.
Dans ce cours, nous allons aborder deux structures de données abstraite : la pile et la file.
La structure du tableau est une structure de données non abstraite. Nous verrons une description de cette structure dans la suite de ce cours.
Intérêts :
L'étude des structures de données abstraite permettent de choisir des structures qui simplifient la compréhension
des algorithmes mais surtout qui permettent d'optimiser en coût de nombreux algorithmes.
Une vidéo en guise d'avant propos :
Un premier exemple : la pile
Pile
Une pile est :
-
soit vide ;
-
soit une cellule à deux champs, un champ contenant un élément, et un champ contenant une autre pile.
On dit que cette structure de est de type LIFO : Last In First Out.
On pourra représenter une pile non vide de la manière suivante :$$P=(hautDeLaPile,resteDeLaPile).$$
Essayons de comprendre ce que cette définition implique :
Pour pouvoir travailler avec des données structurées en pile, il faut déjà pouvoir créer une pile vide. Nous devons nous doter d'une notation synthétique et compréhensible. Pour créer une pile P vide on écrira :
P=vide()
Créer une Pile vide
La structure pile dispose d'un opérateur pour créer une pile P vide. On notera dans ce cours
P=vide()
Pour appliquer la définition à un objet P, nous devons savoir si P est vide ou non.
Il faut donc se doter d'un opérateur estVide qui a un objet de type pile P renvoie un booléen :
Vraie si la pile P est vide et Faux sinon.
La fonction estVide()
À toute pile $P$ :
-
$estVide(P) = Vraie$ si $P$ est vide.
-
$estVide(P) = Faux$ si $P$ n'est pas vide.
Si cette pile n'est pas vide, elle se compose de deux champs : un premier contenant un élément de type élémentaire ( booléen, entier,flottant) et un second de type pile.
Cette définition est donc récursive : une pile est définie à partir d'une pile.
Nous savons ce qu'est une pile vide. C'est une pile dont l'application de l'opérateur
estVide renvoie vraie.
Une pile a un élément est composé dans le haut de sa pile par l'élément et d'une pile vide. Nous avons ainsi compris ce qu'est une pile à un élément :
(a,vide())
Une pile à deux éléments peut être représentées ainsi :
(hautDeLaPile,(secondElementDeLaPile,vide()))
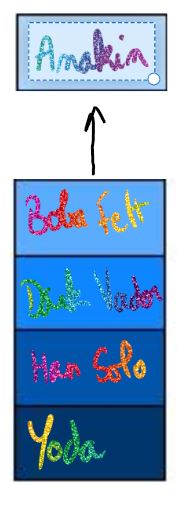
Prenons un exemple, on aimerait ranger un groupe d'individus dans un objet de type pile :
Anakin ; Boba Fett ; Dark Vador ; Han Solo ; Yoda
Un suppose qu'on range d'abord Yoda, puis Han Solo, puis Dark Vador, ensuite Boba Fett et enfin Anakin.
Une représentation de ces données en pile serait :
P=(Anakin,(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide())))))
Le haut de la pile est $Anakin$ et le reste est $(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide()))))$.

-
Donner une représentation en pile de cet ensemble de couleur : $rouge$ rangé après $bleu$, $vert$ étant le premier élément rangé dans la pile. On nommera cette pile $P_{couleur}$.
-
Donner une représentation en pile de cet ensemble de nombres : $12$ rangé avant $5$, puis ranger $3$, puis $6$, puis $1$. On nommera cette pile $P_{entier}$.
À ce stade, vous avez compris ce qu'est une structure de données pile.
Essayons de voir comment manipuler un objet de ce type.
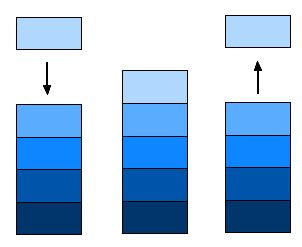
Empiler un élément en haut de pile
Soit P une pile, la pile obtenue en empilant un élément a en haut de P est la pile
(a, P).
On notera cet opérateur empiler(a, P)
En reprenant l'exemple précédent où $ P = (Anakin,(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide())))))$ ,
empiler(Luke,P) conduit à rajouter $Luke$ comme nouvelle
valeur à ranger dans la pile donc on obtient ainsi la pile :
$(Luke,(Anakin,(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide()))))))$

On reprend de l'exercice précédent la pile $P_{couleur}=(Rouge,(Bleu,(Vert,vide())))$. Empiler $violet$ à cette pile.
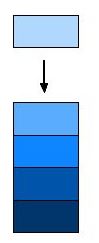
Dépiler le haut d'une pile
Soit P1 une pile et a le haut de la pile de P1 ;
la pile obtenue en dépilant l'élément a de pile de P2 est la pile P2 :
P1 = (a,P2).
On notera depiler(P1) l'opérateur qui transforme la pile initiale P1
en P2 et renvoie l'élément a dépilé.

En reprenant l'exemple précédent où $P = (Anakin,(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide())))))$ ;
la commande depiler(P) transforme la pile $P$ en : $(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide()))))$
et renvoie $Anakin$.
On reprend de l'exercice précédent la pile $P_{couleur}=(violet,(Rouge,(Bleu,(Vert,vide()))))$.
-
Quelle commande permet de retirer la première couleur de cette pile et de l'affecter dans une variable $OT$ ?
-
Quel est l'état de la pile $P_{couleur}$ à l'issue de cette commande ?
Cette structure de pile est utilisée en informatique dès que l'on veut que la dernière donnée arrivée soit la première
à être prise en compte.
On l'utilise ainsi :
-
la plupart des microprocesseurs gèrent nativement des piles,
-
une pile stocke les appels successifs lors de l'utilisation d'une fonction récursive,
-
dans les traitements de texte, la fonction
Undoc'est-à-direannuler la frappe(obtenue sous Windows avec CTRL+Z) supprime le haut de la pile dans laquelle sont mémorisées les modifications apportées au texte, -
L'historique d'un navigateur web utilise une pile,
-
différents algorithmes utilisent des piles, comme nous en verront un exemple cette année avec l'algorithme de recherche en profondeur dans un graphe.
Interface d'une structure de données : définition
Interface d'une structure de données abstraite
L'interface d'une structure de données abstraite est l'ensemble des opérateurs nécessaires à la manipulation de cette structure.
Interface de la pile
L'interface de la structure pile est l'ensemble des opérateurs vus précédemment :
vide()estVide(P)empiler(a,P)depiler(P)
Nous pourrions ajouter d'autres éléments à l'interface mais l'objectif et d'avoir une interface minimale qui permettent de manipuler cette structure.
Il peut être intéressant de connaître le nombre d'éléments dans une pile.
En voila un pseudo-code :
nombreElement=0
while estVide(P) est faux
nombreElement += 1
depiler(P)
renvoyer nombreElementNous n'avons donc pas besoin d'ajouter un opérateur qui compterait le nombre d'éléments d'une pile car on peut en construire avec l'interface minimale donnée précédemment.
On suppose que la structure de données Pile a été implémentée en Python.
On munit les piles des instructions (=primitives) suivantes :
-
vide()renvoie une pile vide, -
empiler(a, pile)ajoute un élémentaen au haut de la pilepile, -
depiler(pile)retourne la valeur retirée en haut de la pilepilemais génère un message d'erreur si la pilepileest vide.
Voici une suite d'instructions :
P1 = vide()
P2 = vide()
empiler("o", P1)
empiler("u", P1)
empiler(3, P2)
x = depiler(P1)
empiler(x, P2)
empiler("i", P1)
empiler(x, P1)
empiler(depiler(P1), P2) Que contiennent les piles P1 et P2 à l'issue de l'exécution de la suite d'instructions précédente ?
Écrire un script en pseudo-code qui permet de supprimer le premier élément du reste d'une pile
(le terme du haut de la pile lui doit rester en haut de la pile obtenue).
L'exécution de ce script va par exemple réduire la pile $("a",("b",("c",("d",vide()))))$ en celle
$("a",("c",("d",vide())))$.
Voici un exercice à faire en autonomie pour tester votre maîtrise
de l'interface usuelle des piles pour créer une nouvelle fonction :
celle donnant la taille d'une pile sans détruire la pile étudiée
contrairement à ce qui se passe dans
l'exemple précédent.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Ne traiter ici que la question Calculer la taille d'une pile en s'aidant de l'animation de la partie Aide et du code de l'exemple précédent.
L'interface de la file
file
Une file est :
-
soit vide ;
-
soit une cellule à trois champs : un champ tête, un champ queue et un champ contenant une file.
Une structure de file fonctionne sur le principe "premier entré - premier sorti" (comme les files d'attentes à un guichet) ; en anglais, on le principe est dit FIFO pour First In First Out.
On pourra représenter une file de la manière suivante :$$F=(teteDeLaFile, queueDeFile, coeurDeFile).$$
-
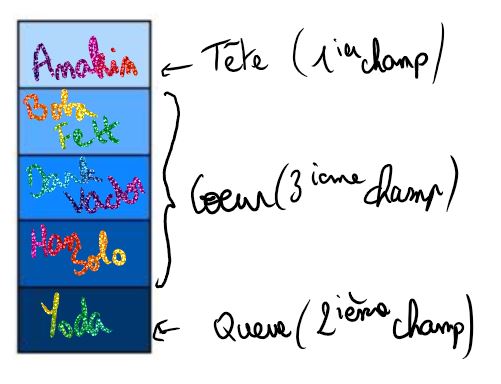
Prenons un exemple, on aimerait ranger dans cet ordre un groupe d'individus dans un objet de type file :
Anakin ; Boba Fett ; Dark Vador ; Han Solo et Yoda.
une représentation en ligne de la file correspondante est :
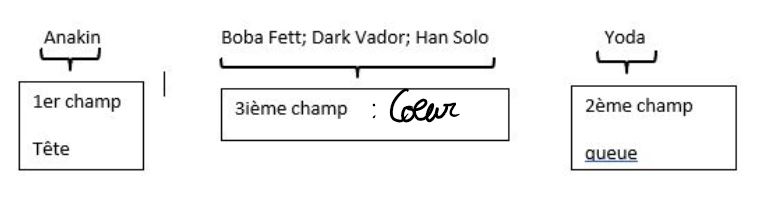
une représentation en colonne de la file correspondante est :
-
Une file à un élément a pour :
-
tête : vide
-
queue : le seul élément
-
troisième champ : vide
-
-
Une file à deux éléments a pour :
-
tête : le premier élément
-
queue : le second élément
-
troisième champ : vide.
-
Définir une file vide
Une file est vide si sa queue est vide.
Pour affecter à une variable F une file vide, on notera :F=vide().
l'enfilement
enfiler(a,F) modifie la file F par l'ajout de a ainsi :
-
la tête de
Fest inchangée ; -
la queue est désormais
a; -
le troisième champ est l'ancien troisième champ de
Fauquel est enfilée l'ancienne queue deF:enfiler(queue de F,troisième champ de F).
Cet opérateur enfiler transforme donc la file et ne renvoie rien.
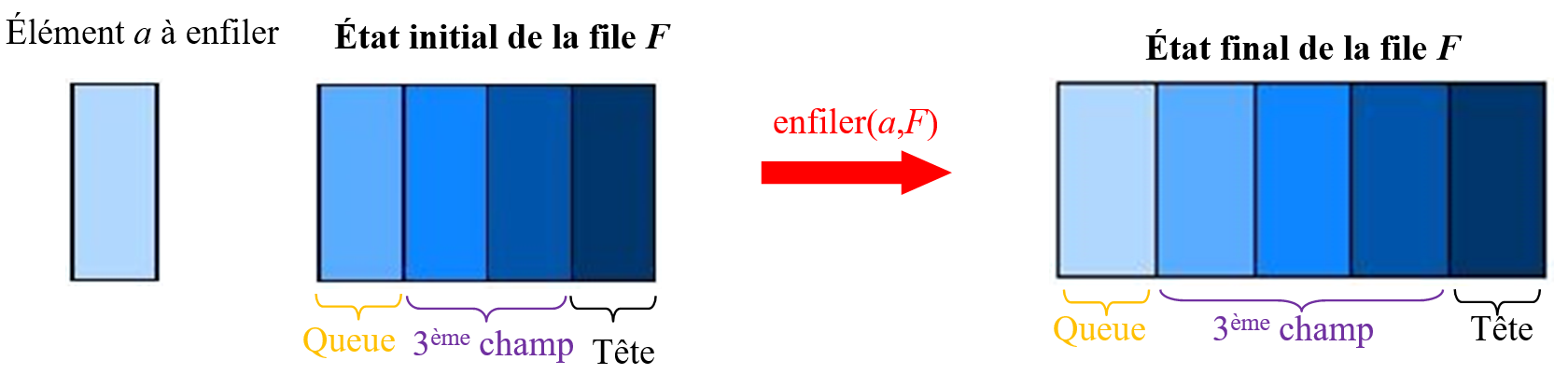
Comme le montre l'évolution du troisième champ, cet opérateur est récursif.
enfiler(queue de F,troisième champ de F) conduit à mettre queue de $F$ à la fin du cœur, le troisième champ, même si cet argument
apparaît en premier lors de l'appel de la fonction enfiler.
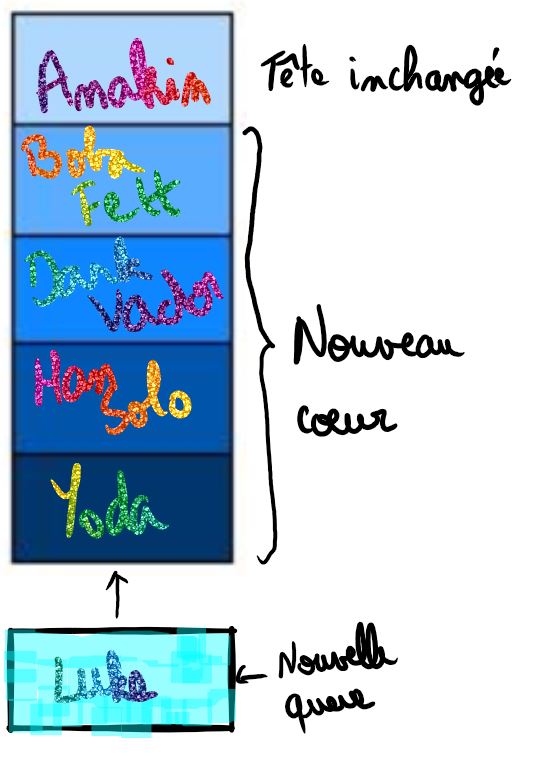
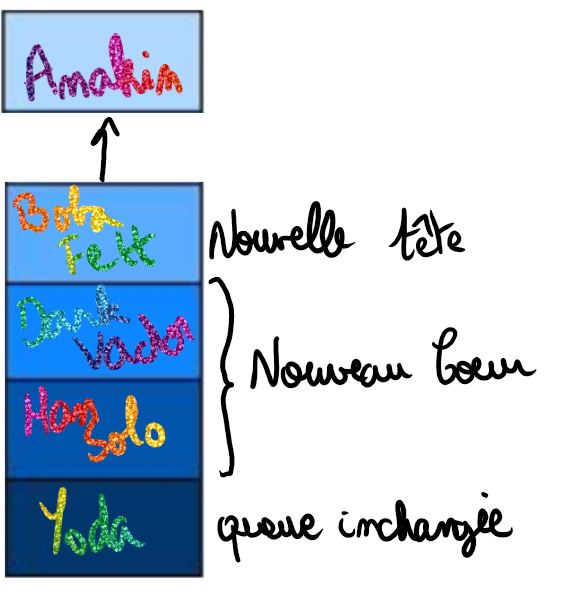
En reprenant l'exemple précédent où $F =(Anakin,Yoda,(Boba Fett,Dark Vador,Han Solo))$; enfiler(Luke,F)
est la file :
$F=(Anakin,Luke,(Boba Fett,Dark Vador,Han Solo,Yoda))$
le défilement
defiler(F) modifie la file F par la suppression de la tête de F et renvoie la tête
défilée ; la file F à la suite du défilement est :
-
de tête, la tête du troisième champ initial de
F; -
de queue inchangée ;
-
le troisième champ est l'ancien troisième champ de
Fauquel a été défilé l'ancienne tête de ce champ, soit le résultat dedéfiler(du troisième champ de F).
Cet opérateur defiler transforme donc la file F et renvoie la tête initiale ôtée de F.
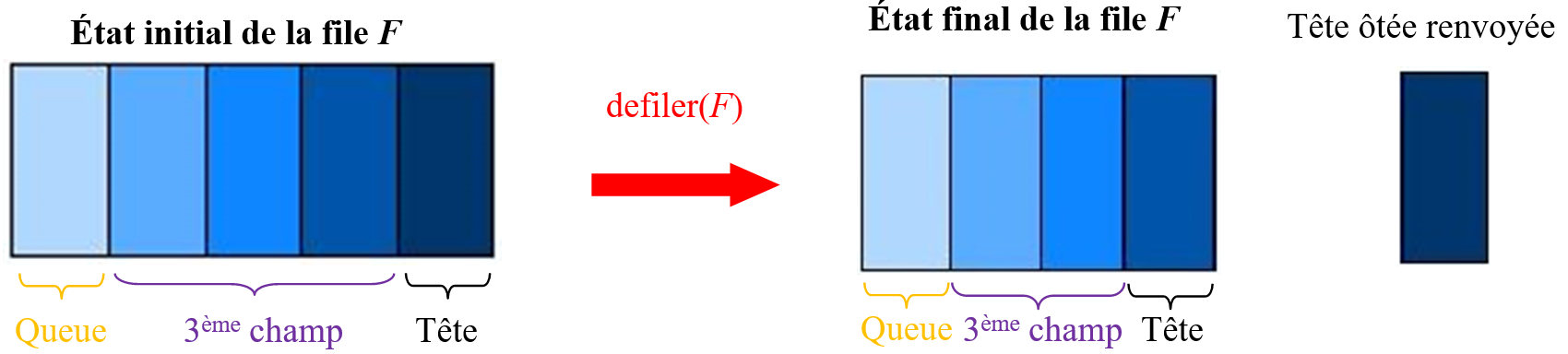
Cet opérateur est lui aussi récursif au vu de la modification du troisième champ.
En reprenant l'exemple précédent où $F=(Anakin,Yoda,(Boba Fett,Dark Vador,Han Solo))$; la commande $defiler(F)$ transforme la file $F$ en : $(Boba Fett,Yoda,(Dark Vador,Han Solo))$ et renvoie Anakin.
interface d'une file
L'interface minimale de la structure de file est composée des opérateurs suivant :
vide()estVide(F)enfiler(a,F)defiler(F)
Il peut être intéressant de connaître le nombre d'éléments dans une file.
En voila un pseudo-code :
nombreElement=0
while estVide(F) est faux
nombreElement+=1
defiler(F)
renvoyer nombreElement
On suppose que la structure de données File a été implémentée en Python.
On munit les files des instructions (=primitives) suivantes :
-
vide()renvoie une file vide, -
enfiler(a,file)ajoute un élémentaen queue de la filefile, -
defiler(file)retourne la valeur retirée en tête de la filefilemais génère un message d'erreur si la filefileest vide. -
est_vide(file)retourneTruesi la filefilepassée en paramètre est vide etFalsesinon.
Voici une suite d'instructions :
F1 = vide()
F2 = vide()
F3 = vide()
for i in range(8):
enfiler(i, F1)
for j in range(3):
enfiler(defiler(F1), F2)
x = defiler(F1)
enfiler(defiler(F1), F2)
for j in range(3):
enfiler(x, F2)
while not est_vide(F1):
enfiler(defiler(F1), F3) Que contiennent les files F1, F2 et F3 à l'issue de l'exécution de la suite d'instructions précédente ?
Écrire un script en pseudo-code qui permet de supprimer le premier élément du troisième champ.
Voici un exercice à faire en autonomie pour tester votre maîtrise
de l'interface usuelle des files
pour créer une nouvelle fonction sans détruire la file étudiée à l'aide d'une file auxiliaire g.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Traiter ici surtout la question Échanger les deux valeurs de tête.
Cette structure de file est utilisée en informatique pour mémoriser les tâches qui doivent attendre pour être effectuées.
On l'utilise ainsi :
-
une imprimante va pouvoir traiter les impressions demandées dans l'ordre d'arrivée des requêtes en mémorisant ces demandes dans une file,
-
un système d'exploitation doit accorder du temps de calcul par les processeurs à chaque tâche. Lorsqu'aucune priorité n'est imposée, une file peut servir à gérer l'octroi du temps-machine aux tâches de même priorité.
-
La mémoire tampon (buffer en anglais) fonctionne sur le principe d'une file.
-
Une structure de données abstraites est une description conceptuelle présentant une image des données et des opérations pour les manipuler et les modifier.
-
L'ensemble des opérations permettant de manipuler et de modifier des données est appelé une interface.
-
La notion de pile est une structure de données abstraites.
Une pile est :
-
soit vide,
-
soit est constituée de deux champs : le haut de la pile et le reste de la pile.
L'interface élémentaire de la pile consiste en :
-
un constructeur
pile()qui permet de créer une pile vide, -
un testeur
est_vide(P)qui permet de tester de tester si une pilePest vide ou non, -
un empileur
empiler(a,P)qui permet d'ajouter un élémentaen haut de la pileP, -
un dépileur
depiler(P)qui permet d'enlever le haut de la pilePet de le renvoyer.
-
-
La notion de file est une autre structure de données abstraites.
Une file est :
-
soit vide,
-
soit est constituée de trois champs : une tête, un corps et une queue.
L'interface élémentaire de la file consiste en :
-
un constructeur
file()qui permet de créer une file vide, -
un testeur
est_vide(F)qui permet de tester de tester si une fileFest vide ou non, -
un enfileur
enfiler(a,F)qui permet d'ajouter un élémentaen queue de la fileF, -
un défileur
defiler(F)qui permet d'enlever la tête de la fileFet de le renvoyer.
-
Implémentation
Implémentation
Implémenter une structure de données à travers une structure existante c'est écrire les éléments de l'interface à l'aide des outils proposées par la structure de données existante.
Tableau
Tableau
Un tableau est une structure de données avec une taille fixe où chacune des cases est indexée. On peut accéder à une case connaissant son index.
Accès à une valeur d'un tableau
Pour accéder à une valeur indexée $i$ dans un tableau T. On écrira T[i].
On peut réaffecter une valeur du tableau par une autre à partir de son index.
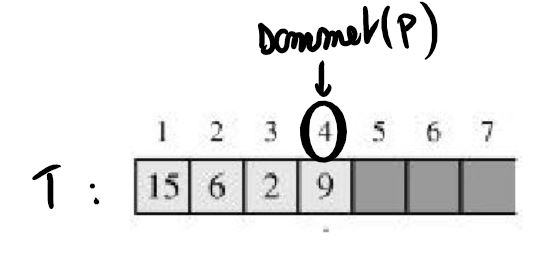
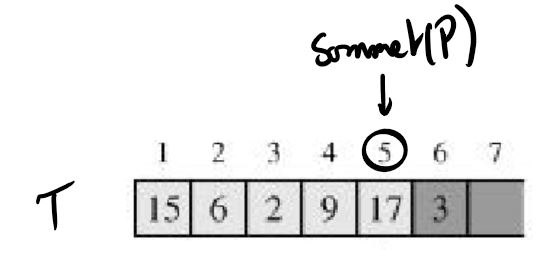
Ce tableau a une longueur maximale de 7. T[1]=15. T[5] est vide.
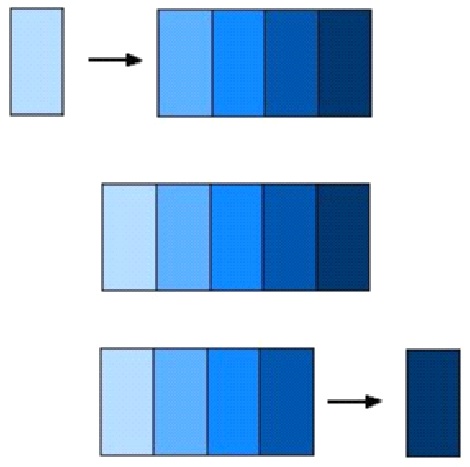
implémentation des piles avec des tableaux
Soit $P$ une pile.
On dispose d'un tableau nommé $T$ avec $n$ emplacements.
Il est possible d’implémenter la pile $P$ d’au plus $n$ éléments avec le tableau $T$.
Le tableau possède un attribut $sommet(P)$ qui indexe l’élément le plus récemment inséré.
La pile est constituée des éléments $T[1 . . sommet(P)]$, tous ceux compris entre $T[1]$, l’élément situé à la base de la pile, et $T[sommet(P)]$, l’élément
situé au sommet.
La donnée de la pile se constitue donc de la donnée de $T$ et de la valeur de $sommet(P)$.
On considère la pile $(9,(2,(6,(15,vide()))))$. Son implémentation se compose de la donnée du tableau T:

et de $sommet(P)=4$.
$sommet(P)$ est un index du tableau, pas un élément de la pile.
Implémentation de la fonction estVide(P)
estVide(paramètre : P)
si sommet(P)=0 //signifie que le tableau est vide
alors retourner VRAI
sinon retourner FAUX Implémentation de la procédure empiler(a,P)
empiler(paramètres : a,P)
si sommet(P)=n //signifie que le tableau est complet
alors afficher "espace insuffisant"
sinon
sommet(P)←sommet(P)+1
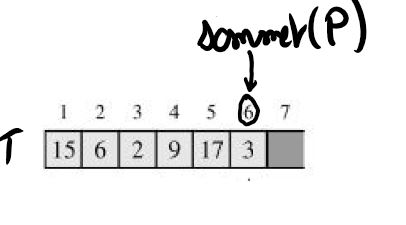
T[sommet(P)]←a Si on lance empiler(17,P) puis empiler(3,P) on obtient cette représentation :
Implémentation de la fonction depiler(P)
depiler(paramètre : P)
si sommet(P)=0
alors afficher "pile vide"
sinon sommet(P)←sommet(P)-1
retourner T[sommet(P)+1] On observe que la procédure empiler ne renvoie rien alors que la fonction depiler renvoie un élément de la pile.
Si on lance depiler(P) on obtient :
Observer que T[6] a encore un sens pour le tableau mais plus pour la pile.
On considère la pile dont la représentation en tableau est :

Pour chaque question, on repartira du tableau de départ.
-
Qu'obtient-on si on lance successivement
depiler(P),depiler(P),depiler(P)etdepiler(P). -
Qu'obtient-on si on lance successivement
depiler(P),depiler(P),depiler(P),depiler(P)etdepiler(P). -
Qu'obtient-on si on lance successivement
empiler(3, P),empiler(5, P)etdepiler(P).
implémentation des files avec des tableaux
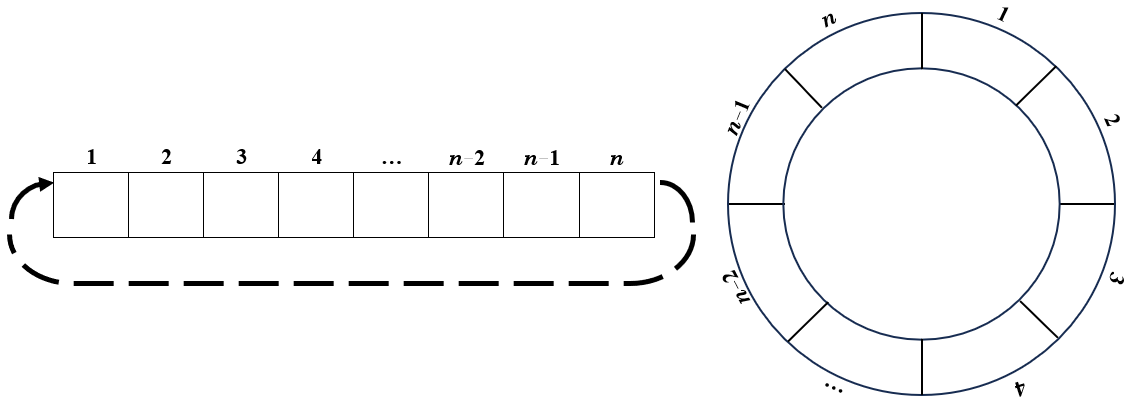
On dispose d'un tableau nommé $T$ avec $n$ emplacements.
Il est possible d’implémenter une file $F$ d’au plus $n-1$ éléments avec le tableau $T$.
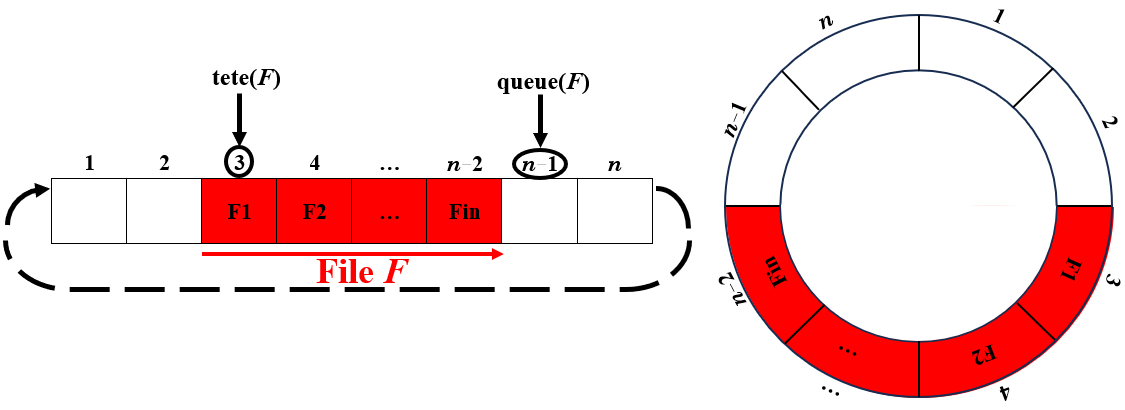
Le tableau possède un attribut $tete(F)$ qui indexe l’élément de tête et un attribut $queue(F)$ qui indexe l'emplacement où un nouvel élément sera inséré. $T[queue(F)]$ est vide au sens de la file. Ainsi, le tableau devra toujours avoir au moins une case libre, ce qui explique qu'un tableau de taille $n$ permettra d'implémenter une pile d'au plus $n-1$ éléments.
La file est constituée des éléments $T[tete(F) . . queue(F)-1]$.
Avec cette implémentation $T[n+1]$ doit pointer vers $T[1]$ au sens de la file. Une façon de visualiser cette implémentation est un tableau circulaire où le début du tableau et la fin du tableau seraient reliés.
Les éléments de la file se trouvent aux emplacements $tete(F)$, $tete(F) +1$, . . . , $queue(F) − 1$ :
 Avec la convention que l’on « boucle » : l’emplacement 1 suit immédiatement l’emplacement $n$ dans un ordre circulaire :
Avec la convention que l’on « boucle » : l’emplacement 1 suit immédiatement l’emplacement $n$ dans un ordre circulaire :
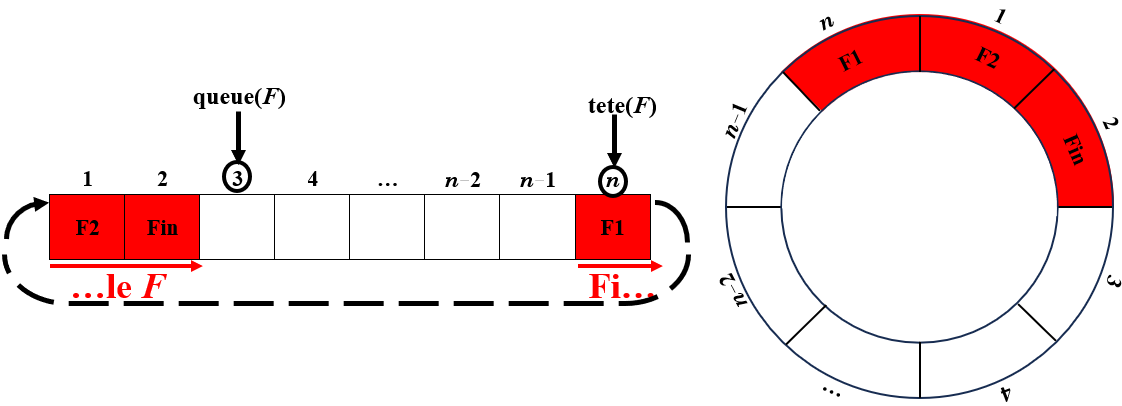
Attention ! Dans cette implémentation la queue est vide
La donnée de la file se constitue de la donnée d'un tableau $T$, de la valeur de $tete(F)$ et de $queue(F)$.
Une représentation de l'implémentation avec un tableau $T$ de la file $F=(15,4,(6,9,8))$ est :
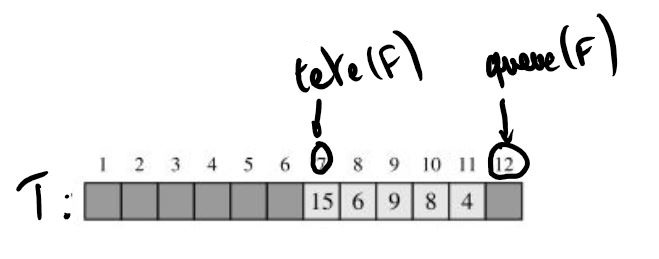
-
Quand $tete(F) = queue(F)$, la file est vide.
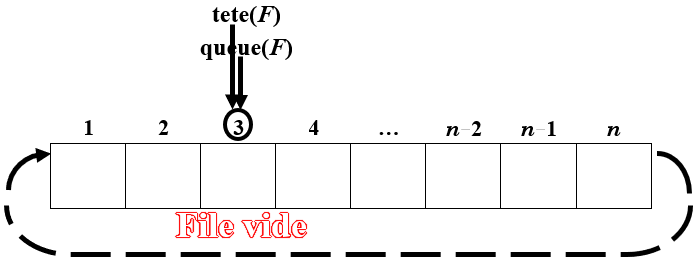
-
Quand $tete(F) = queue(F) + 1$, la file est pleine.
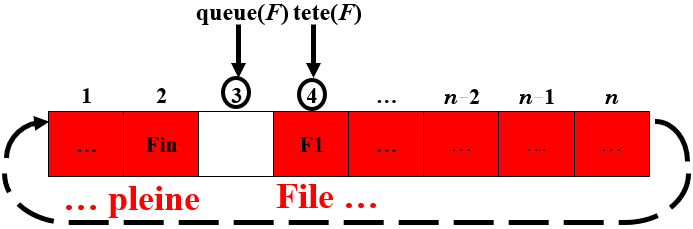
-
Par définition, $queue(F)$ désigne un emplacement vide du tableau. Si $tete(F) = queue(F)$ alors la tête est vide, c'est que la file est vide.
-
L'emplacement $queue(F)$ doit toujours être vide au sens de la file.
Or, si $tete(F) = queue(F) + 1$, le prochain enfilage conduira au fait que $tete(F) = queue(F)$ si bien que $queue(F)$ ne serait plus vide, ce qui est impossible.
Ainsi, si $tete(F) = queue(F) + 1$, il n'y a pas d'enfilage possible : la file est donc pleine.
Cela est cohérent avec l'affirmation initiale qu'un tableau à $n$ emplacements ne peut implémenter qu'une file d'au plus $n-1$ éléments.Du fait de la circularité, il faut comprendre cette égalité au sens mathématique "modulo $n$", c'est-à-dire "à $n$ près".
En effet, dans le cas où la tête est en $1$ et la queue en $n$, la file est pleine (car emplie de $1$ à $n-1$) et l'égalité $tete(F) = queue(F) + 1$ est vrai à un écart $n$ près entre les deux membres.
Implémentation de la fonction estVide(F)
estVide(F)
si queue(F)=tete(F)
alors retourner VRAI
sinon retourner FAUX Implémentation de la fonction enfiler(a,F)
enfiler(a,F)
T(queue(F))←a
si queue(F)=n
alors queue(F)←1
sinon queue(F)←queue(F)+1 On dispose d'une file dont la représentation de l'implémentation en tableau est :

Si on lance enfiler(17,F) puis enfiler(3,F) et enfin
enfiler(5,F), on obtient cette représentation :
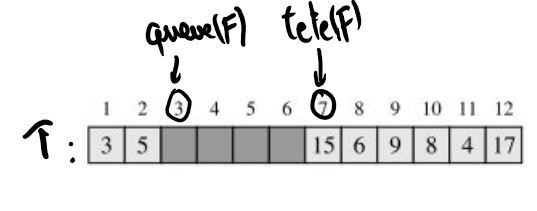
Implémentation (simplifiée) de la fonction defiler(F)
Dans le pseudo-code suivant, $F$ désigne une file (supposée non vide) et $n$ correspond à la taille fixe du tableau servant à l'implémentation de la file.
defiler(F)
x←T[tete(F)]
si tete(F)=n
alors tete(F)←1
sinon tete(F)←tete(F)+1
retourner x On dispose de la file de l'exemple précédent :

Si on lance defiler(F), on obtient :
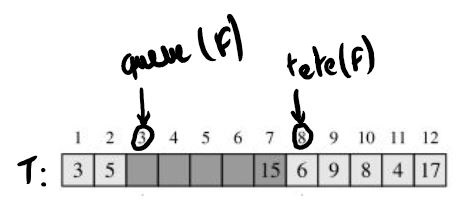
Observer que T[7] a encore un sens pour le tableau mais plus pour la file.
On considère la file dont la représentation de l'implémentation en tableau est :
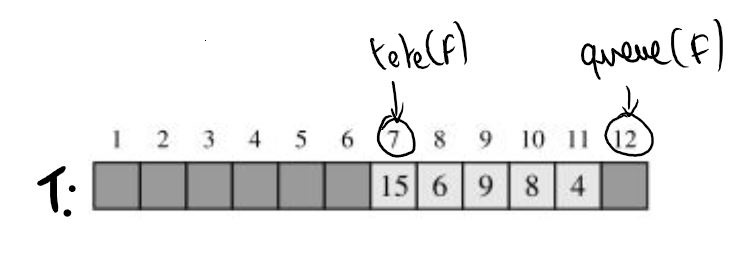
-
Qu'obtient-on si on lance successivement
defiler(F),defiler(F),defiler(F)etdefiler(F). -
Qu'obtient-on si on lance successivement
defiler(F),defiler(F),defiler(F),defiler(F)etdefiler(F). -
Qu'obtient-on si on lance successivement
enfiler(3,F),enfiler(5,F)etdefiler(F).
Reprendre la fonction $enfiler()$ de la propriété où elle a été implémentée et y ajouter les erreurs de dépassements d'écritures.
Exercices
On suppose que la structure de données Pile a été implémentée en Python.
On munit les piles des trois instructions (=primitives) suivantes :
-
vide()renvoie une pile vide, -
empiler(a, pile)ajoute un élémentaen au haut de la pilepile, -
depiler(pile)retourne la valeur retirée en haut de la pilepilemais génère un message d'erreur si la pilepileest vide.
Voici une suite d'instructions :
P1 = vide()
P2 = vide()
P3 = vide()
for i in range(12):
empiler(i, P1)
for j in range(3):
empiler(depiler(P1), P2)
depiler(P1)
empiler(depiler(P1), P3) Que contiennent les piles P1, P2 et P3 à l'issue de l'exécution de la suite d'instructions précédente ?
On suppose que la structure de données Pile a été implémentée en Python.
On munit les piles des quatre instructions (=primitives) suivantes :
-
vide()renvoie une pile vide, -
empiler(a, pile)ajoute un élémentaen au haut de la pilepile, -
depiler(pile)retourne la valeur retirée en haut de la pilepilemais génère un message d'erreur si la pilepileest vide.
-
En utilisant les quatre primitives sur les piles, proposer une fonction
hauteur, qui prend en paramètre une pile et renvoie l'entier naturel correspondant au nombre d'élément de la pile entrée comme argument.
Attention ! Faire en sorte que le contenu de la pile saisie comme argument ne soit pas modifié à l'issue de l'exécution de la fonctionhauteur. -
De même, proposer une fonction
renverserqui prend en paramètre une pile et renvoie une pile formée des mêmes éléments que la pile saisie comme argument mais dont l'ordre est inversé.
Faire aussi en sorte que la pile saisie comme argument ne soit pas modifiée à l'issue de l'exécution de cette fonctionrenverser.
Exercices du bac
Implémentation d'une file à l'aide de deux piles
Dans cet exercice, on choisit d'implémenter une file file à l'aide de d'un couple
(entree, sortie) où entree et sortie sont deux piles.
Ainsi file[0] correspond à entree et file[1] à sortie.
Par exemple la file ci-contre : 
peut être implémentée par les deux piles suivantes : 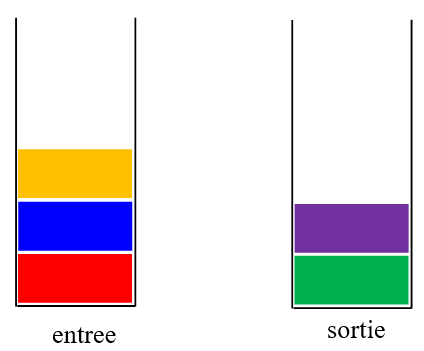
tout comme par les deux piles suivantes : 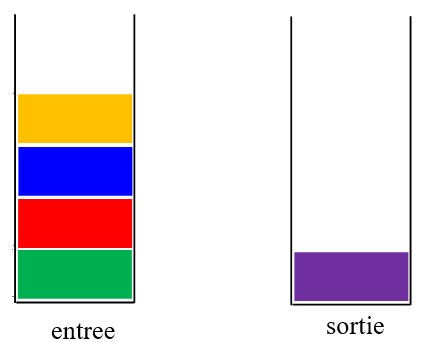
Voici le fonctionnement de cette file :
-
la pile
entreecontient les éléments que l'on insère dans la file tandis que la pilesortiecontient les éléments que l'on retire de la file. -
la file est vide lorsque les deux piles
entreeetsortiesont vides. -
enfiler un nouvel élément
eltdans la file revient à empiler cet élément dans la pileentree.Voici une illustration de
enfiler(elt, file):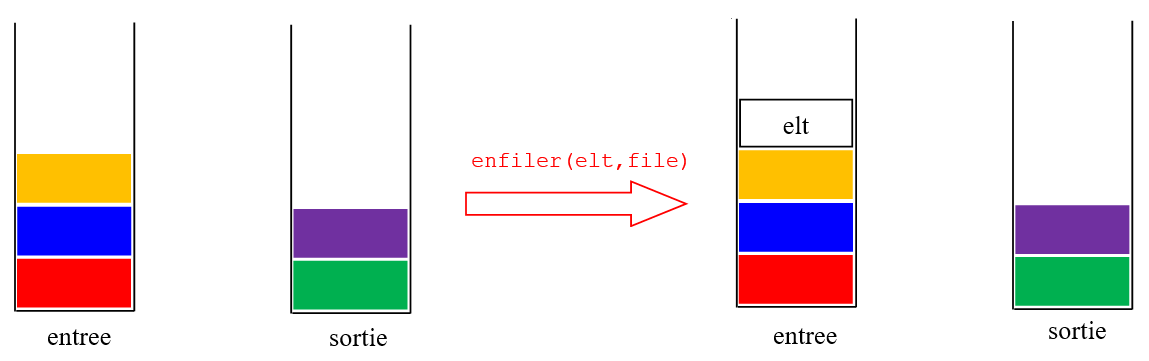
-
defiler un élément de la file, il faut que celle-ci ne soit pas vide. Alors, deux cas se présentent :
-
la pile
sortien'est pas vide : on dépile cette pilesortie,Voici une illustration de
defiler(file)dans ce cas :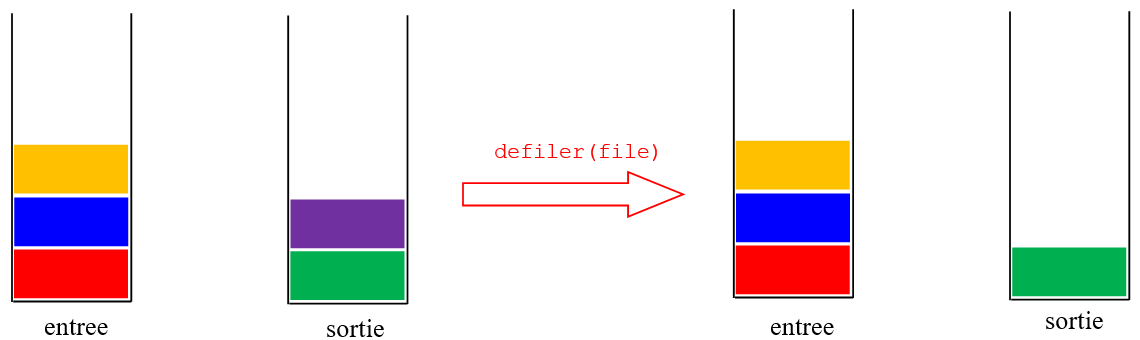
-
la pile
sortieest vide : on dépile alors les éléments de la pileentreeun à un en les empilant dans la pilesortiejusqu'à ce queentreesoit vide ; ensuite, on dépile un élément de la pilesortie.Voici une illustration de
defiler(file)dans ce cas :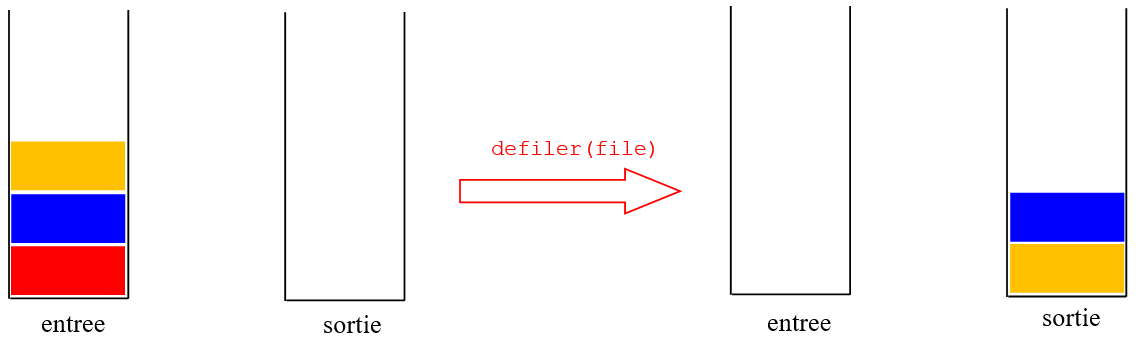
-
-
On suppose que la file
fileest dans l'état correspondant à la figure suivante :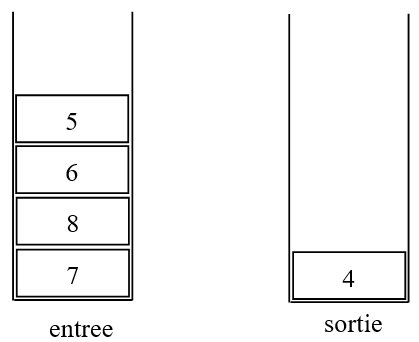
On exécute la séquence d'instructions suivantes :
enfiler(1, file) defiler(file) defiler(file) enfiler(2, file) defiler(file)Représenter le contenu final des deux piles représentant la file
fileà la suite de ces instructions. -
A la suite des instructions déjà effectuées précédemment, on exécute la séquence d'instructions suivantes :
defiler(file) enfiler(3, file) enfiler(defiler(file), file)Représenter le contenu final des deux piles représentant la file
fileà la suite de ces instructions. -
On suppose disposer des fonctions suivantes écrite en langage Python :
-
empiler(elt, pile)qui empile l'élémenteltsur la pilepile, -
depiler(pile)qui dépile le sommet de la pilepile, si elle n'est pas vide, et renvoie ce sommet, -
pile_vide(pile)qui renvoie le booléenTruesi la pilepileest vide etFalsesinon.
-
Écrire en langage Python une fonction
est_vide(file)qui prend en argument une filefileconstituée d'un couple de piles et qui renvoieTruesi la filefileest vide etFalsesinon. -
Écrire en langage Python une fonction
enfiler(elt, file)qui prend en argument un entiereltet une filefileconstituée d'un couple de piles et qui ajouteelten queue de la filefile. -
Écrire en langage Python une fonction
defiler(file)qui prend en argument une filefile, supposée non vide, constituée d'un couple de piles et qui renvoie l'élément en tête de la filefileen en le retirant.
-
Il est possible d'implémenter une pile sous forme d'une liste Python en utilisant la méthode
append() pour empiler et celle pop() pour dépiler le sommet.
Programmer les trois fonctions empiler(elt, pile), depiler(pile) et
pile_vide(pile) de l'exercice précédent en implémentant une pile comme une liste
Python.
Il existe une implémentation spécifique pour les piles et les files dans le module queue (cf. documentation officiel )
Nous verrons au prochain chapitre la programmation objet qui permettra d'implémenter aussi ces types abstraits.
Savoir faire et Savoir
- Comprendre l'évolution d'une pile suite à l'exécution d'un ensemble d'opérateurs,
- Comprendre l'évolution d'une file suite à l'exécution d'un ensemble d'opérateurs,
- Implémenter une pile à l'aide d'un tableau, d'une liste (ou en programmation objet),
- Implémenter une file à l'aide d'un tableau, de deux piles (ou en programmation objet),
- La notion de structure de données abstraite,
- La notion d'interface d'une structure de données abstraite,
- la notion d'implémentation d'une structure de données abstraite,
- La structure d'une pile avec son interface réduite,
- La structure d'une file avec son interface réduite,
- la notion de tableau comme structure de données abstraire.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International