- SD1
- SD2
- DC2 (première)
Le type abstrait liste
Structure de données linéaire
Une structure de données est dite linéaire si on peut la représenter sous forme linéaire
(en ligne).
Les files et les piles vues dans le cours sd1 sont des structures linéaires
Un exemple de file :
un exemple de pile :

-
Nous verrons par la suite des structures non linéaires :
Arbre :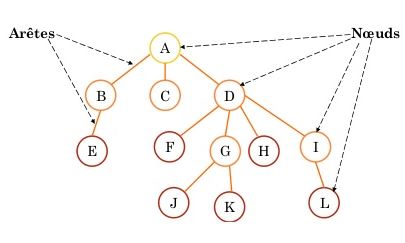
Graphe :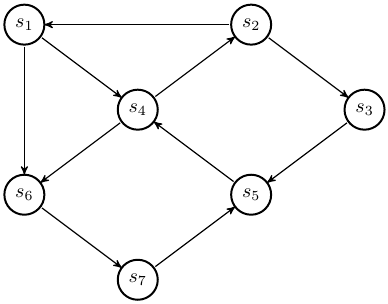
-
Dans ce cours, nous allons voir deux autres structures linéaires les listes et les dictionnaires.
Le type abstrait liste
Liste
Une liste est une structure de données d'éléments indicés à partir de 0.
Dans cette structure de données, il est possible d'ajouter et supprimer des éléments à une liste.
$L=\{Bob;x;A7;1011;f\}$
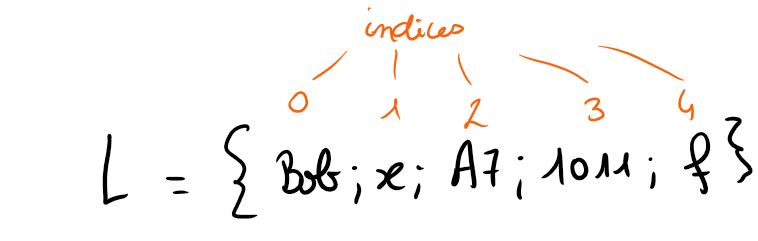
Dans cette liste, l'élément indicé 2 est A7
Cette liste dispose de 5 éléments
Interface d'une liste
-
$listeVide$ : créer une liste vide.
-
$ajouteEnFin(x,L)$ : ajoute à la fin de $L$ l'élément x.
-
$dernier(L)$ : renvoie le dernier élément de $L$.
-
$debut(L)$ : renvoie le premier élément de la liste $L$;
-
$supprDernier(L)$ : supprime le dernier élément de L.
-
$taille(L)$ : renvoie le nombre d'éléments dans $L$.
-
$get(i,L)$ : renvoie l'élément d'indice $i$ de $L$.
On considère la liste abstraite $L=\{Bob;x;A7;1011;f\}$
-
$ajouteEnFin(25,L)$ fait que $L=\{Bob;x;A7;1011;f;25\}$.
-
$dernier(L)$ renvoie alors 25.
-
$debut(L)$ renvoie la $Bob$.
-
$supprDernier(L)$ fait que $L=\{Bob;x;A7;1011;f\}$.
-
$taille(L)$ renvoie 5.
-
$get(4,L)$ renvoie $f$.
On donne $L=\{NSI; plaisir; jeux; livres; \pi; E0F1\}$
Expliciter ce que font indépendamment chacune des commandes suivantes :
-
$ajouteEnFin(33,L)$ .
-
$dernier(L)$.
-
$debut(L)$ .
-
$supprDernier(L)$.
-
$taille(L)$.
-
$get(2,L)$.
Les piles et les files sont des listes particulières, elle répondent à des problèmes où des structures de type LIFO FIFO sont adaptées.
Implémentation des listes avec des tableaux dynamiques
Tableaux dynamiques.
Une structure de données est dite linéaire si on peut la représenter sous forme linéaire (en ligne).
Les files et les piles vues dans le cours sd1 sont des structures linéaires
Un exemple de file :

un exemple de pile :

-
Nous verrons par la suite des structures non linéaires :
Arbre :

Graphe :

-
Dans ce cours, nous allons voir deux autres structures linéaires les listes et les dictionnaires.
Liste
Une liste est une structure de données d'éléments indicés à partir de 0.
Dans cette structure de données, il est possible d'ajouter et supprimer des éléments à une liste.
$L=\{Bob;x;A7;1011;f\}$
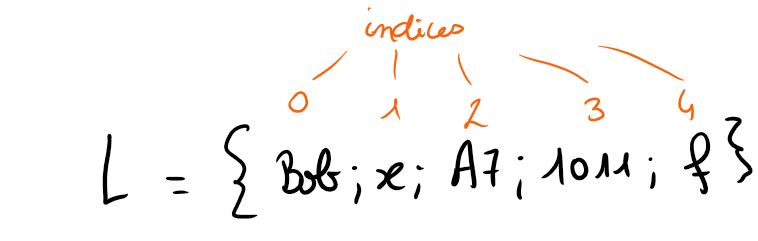
Dans cette liste, l'élément indicé 2 est A7
Cette liste dispose de 5 éléments
Interface d'une liste
-
$listeVide$ : créer une liste vide.
-
$ajouteEnFin(x,L)$ : ajoute à la fin de $L$ l'élément x.
-
$dernier(L)$ : renvoie le dernier élément de $L$.
-
$debut(L)$ : renvoie le premier élément de la liste $L$;
-
$supprDernier(L)$ : supprime le dernier élément de L.
-
$taille(L)$ : renvoie le nombre d'éléments dans $L$.
-
$get(i,L)$ : renvoie l'élément d'indice $i$ de $L$.
On considère la liste abstraite $L=\{Bob;x;A7;1011;f\}$
-
$ajouteEnFin(25,L)$ fait que $L=\{Bob;x;A7;1011;f;25\}$.
-
$dernier(L)$ renvoie alors 25.
-
$debut(L)$ renvoie la $Bob$.
-
$supprDernier(L)$ fait que $L=\{Bob;x;A7;1011;f\}$.
-
$taille(L)$ renvoie 5.
-
$get(4,L)$ renvoie $f$.
On donne $L=\{NSI; plaisir; jeux; livres; \pi; E0F1\}$
Expliciter ce que font indépendamment chacune des commandes suivantes :
-
$ajouteEnFin(33,L)$ .
-
$dernier(L)$.
-
$debut(L)$ .
-
$supprDernier(L)$.
-
$taille(L)$.
-
$get(2,L)$.
Les piles et les files sont des listes particulières, elle répondent à des problèmes où des structures de type LIFO FIFO sont adaptées.
Implémentation des listes avec des tableaux dynamiques
Tableaux dynamiques.
Les tableaux ont des tailles fixes alors que les listes non. C'est pour cela qu'il nous faut des tableaux dynamiques.
Un tableau dynamique est un tableau dont la taille peut varier. Ainsi, si on a besoin d'ajouter un élément à un tableau, on crée un nouveau tableau plus grand, on copie les éléments de l'ancien tableau dans le nouveau, on ajoute le nouvel élément à la fin, on remplace l'ancien tableau par le nouveau, et enfin on supprime l'ancien tableau.
Les opérations possibles avec le tableaux dynamiques :
-
$tableVide$ : créer un tableau dynamique vide.
-
$get(T,k)$ : renvoie l'élément indicé $k$ dans le tableau $T$.
-
$suppre(T,k)$: supprime l'élément d'indice $k$.
-
$ajoute(T,x)$: ajoute l'élément $x$ à la fin du tableau.
Implémentation des listes.
L'utilisation de tableaux dynamiques est l'implémentation choisie par le langage Python pour intégrer les listes.
Cette implémentation est efficace pour accéder à des éléments de la liste mais l'est beaucoup moins pour insérer des éléments. En effet insérer un élément oblige à décaler tous les éléments un par un. C'est pourquoi une autre implémentation est possible celle avec les listes chaînées.
Voici un exercice à faire en autonomie pour vérifier l'affirmation
de la remarque précédente : le coût de l'insertion dans un tableau
dynamique de type list en Python est linéaire dans
le pire des cas et non constant.
Cet exercice est issu du site d'un collègue de NSI Jean Diraison.
Une aide est disponible en cliquant sur l'onglet en bas Indication.
Une fois le code complété, cliquer sur les boutons Exécuter pour
exécuter votre script et Vérifier la réponse afin de tester votre script
sur des quelques cas.
À la dixième vérification, une proposition de correction est affichée afin de vous aider à progresser.
Implémentation de listes avec des listes simplement chaînées.
Listes simplement chaînées.
liste simplement chaînée
Une liste simplement chaînée est une structure de données dans laquelle les objets sont arrangés linéairement. Toutefois, contrairement au tableau, pour lequel l’ordre linéaire est déterminé par les indices, l’ordre d’une liste chaînée est déterminé par un pointeur dans chaque objet.
À partir d'un élément $x$ d'une liste simplement chaînées, on peut accéder à l'élément suivant, noté $succ[x]$.
Chaque élément $x$ d’une liste simplement chaînée $L$ est un objet comportant 2 champs :
-
un champ clé (le nom de la variable qui contient la donnée) noté $clé[x]$,
-
un deuxième champ pointeur noté $pointeVers[succ[x]]$ qui pointe vers le prochain élément de la liste.
On peut ainsi noté un élément $x$ d'une liste $L$ ainsi : $(cle[x],pointeVers[succ[x]])$.
À chaque liste $L$, on peut disposer de sa tête : on notera $tete[L]$ le premier élément d'une liste.
On notera NIL la valeur du pointeur qui ne pointe sur rien. Ce sera le marqueur de fin de la liste.
Ainsi les données : $\{\alpha; \gamma; \phi; \beta\}$ peut être représentées avec une liste simplement chaînée ainsi :
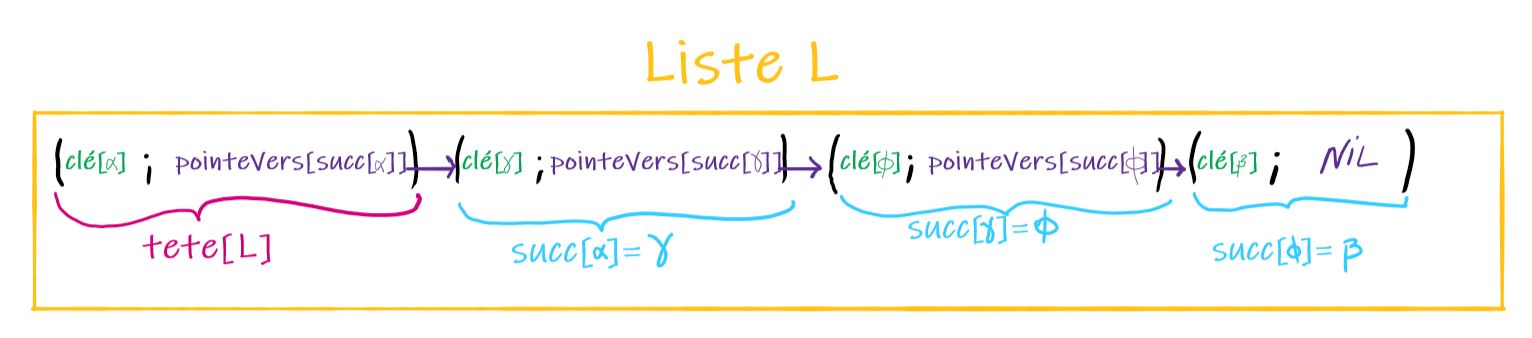
Il faut avoir en tête que la modification d'un pointeur a un coût très inférieur à la réaffectation d'un élément.
Voici une vidéo qui illustre concrètement la notion de liste chaînée et qui permet de comprendre pourquoi modifier un pointeur a un coût très inférieur à la réaffectation d'un élément.
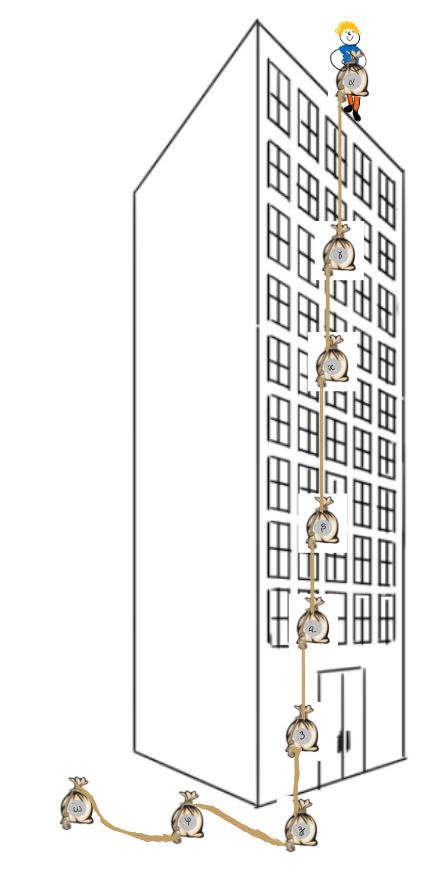
Voici une représentation visuelle de la liste abstraite contenant les données $\{\alpha;\gamma;x;\beta;a;3;z;\phi;\omega\}$ :
Interface des listes simplement chaînées
L'interface des listes simplement chaînées se compose des éléments suivants :
-
$creerListeVide()$ : qui créer une liste vide.
-
$estVide(L)$: qui renvoie un booléen. vrai pour une liste vide et Faux pour une liste non vide.
-
$tete(L)$ : permet d'accéder à la tête de $L$.
-
$succ[x]$ : permet d'accéder au successeur de $x$ (s'il existe) où $x$ est un élément de $L$.
-
$cle[x]$ : permet d'accéder à la clé de $x$ où $x$ est un élément de $L$.
La liste vide est composée d'un premier champ clé vide et d'un second champ NIL. 
On propose la fonction, écrite en pseudo code, $mystere(L, i)$ où $L$ est une liste et $i$ une clé de cette liste :
1. mystere(L, i)
2. x = tete[L]
3. si cle[x] == i
4. tete[L] = succ[x]
5. sinon
6. tant que cle[x] != i et pointeVers[succ[x]] != NIL
7. y = x
8. x = succ[x]
9. fin tant que
10. pointeVers[succ[y]] = pointeVers[succ[x]]-
Effectuer une trace d'exécution de $mystere(L, cle[\alpha])$, où $L$ est la liste simplement chaînée contenant les valeurs $\{\alpha;\gamma;x;\beta;a;3;z;\phi;\omega\}$, liste simplement chaînée représentée ici, en reproduisant et en complétant le tableau suivant :
Numéro de ligne $x$ $succ[x]$ $i$ $L$ $y$ $pointeVers[succ[y]]$ $pointeVers[succ[x]]$ $tete[L]$ Test ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
De même, effectuer une trace d'exécution de $mystere(L, cle[a])$ où $L$ est la liste simplement chaînée contenant les valeurs $\{\alpha;\gamma;x;\beta;a;3;z;\phi;\omega\}$, liste simplement chaînée représentée ici.
Proposer un nom pertinent pour la fonction $mystere$ en comprenant le rôle de cette fonction.
On propose la fonction $mystere(L, k)$ où $L$ est une liste et $k$ une clé de cette liste suivante écrit en pseudo code :
1. mystere(L, k)
2. x = tete[L]
3. tant que cle[x]!=k et pointeVers[succ[x]]!=NIL
4. x = succ[x]
5. fin tant que
6. renvoyer x
-
appliquer $mystere(L, cle[\alpha])$, où $L$ est la liste simplement chaînée contenant les valeurs $\{\alpha;\gamma;x;\beta;a;3;z;\phi;\omega\}$, liste simplement chaînée représentée ici..
-
appliquer $mystere(L,cle[a])$, où $L$ est la liste simplement chaînée contenant les valeurs $\{\alpha;\gamma;x;\beta;a;3;z;\phi;\omega\}$, liste simplement chaînée représentée ici..
-
Proposer un nom pour la fonction $mystere$.
-
Que pensez-vous de la seconde condition de la boucle tant que
pointeVers[succ[x]]!=NIL.
Écrire en pseudo code les fonctions suivantes :
-
$longueur(L)$ : qui renvoie le nombre d'élément dans la liste.
-
$insererEnDebut(L, x)$ : L'élément $x$ (de la forme ($clé[x]$, $pointeVers[succ[x]]$)) est inséré à la tête de la liste. (Seule la donnée de l'élément $x$ est insérée, le pointeur dépend de la liste $L$).
-
$inserer(L, a, e)$ : L'élément $e$ est inséré après l'élément de clé $a$ présent dans la liste $L$. (Seule la donnée de l'élément $e$ est insérée, son pointeur est adapté à la liste $L$).
Implémentation des listes avec des listes simplement chaînées.
L'objectif de cette partie est d'écrire les éléments de l'interface d'une liste :
-
$listeVide$ : créer une liste vide.
-
$dernier(L)$ : renvoie le dernier élément de $L$.
-
$ajouteEnFin(x,L)$ : ajoute à la fin de $L$ l'élément $x$.
-
$debut(L)$ : renvoie la liste $L$ auquel on a retiré le dernier élément.
-
$supprDernier(L)$ : supprime le dernier élément de $L$.
-
$taille(L)$ : renvoie le nombre d'éléments dans $L$.
-
$get(i, L)$ : renvoie l'élément d'indice $i$ de $L$.
À l'aide des éléments vus dans la partie précédente.
Écrire chaque élément de l'interface à l'aide des fonctions écrites dans la propriété sur l'interface des listes simplement chaînées ainsi que celles obtenues aux exercices 2 à 4 précédant.
Implémentation de l'objet liste simplement chaînée en Python à partir des listes de Python
Créer la classe ListeSimpleCh qui possède comme attribut un objet de type list et sa tête à partir des listes en Python. On donne Le constructeur __init__(self, l, tete) avec deux attributs une liste $l$ et une $tete$
:
class ListeSimpleCh:
"""définition de l’objet liste"""
def __init__(self, l, tete):
self.l = l
self.t = tete
Créer une instanciation de la classe ListeSimpleCh avec la liste [1, 'bos', 4, "BG", 0]. Afficher la tete de liste.
Vous devez ajouter à cette classe :
-
La méthode
estVide(self)qui teste si une liste est vide. -
L'accesseur
tete(self)qui renvoie la tête de la liste. -
L'accesseur
succ(self, x)qui renvoie le successeur de $x$ en vérifiant que ce successeur existe (faire desassert).
Écrire les fonctions suivantes en Python à partir de la classe définie précédemment :
Comme l'objet de cette classe a comme premier attribut une liste Python, vous pouvez utiliser l'ensemble des méthodes connues sur ces listes Python.
-
$supprimer(L, i)$ : L'élément de clé $i$ est supprimé de la liste.
-
$rechercheListe(L, k)$ : qui retourne l'index du premier objet de clé $k$.
-
$longueur(L)$ : qui renvoie le nombre d'élément dans la liste.
-
$insererEnDebut(L, x)$ : L'élément $x$ est inséré à la tête de la liste.
Implémentation de l'objet liste simplement chaînée en Python en programmation objet
L'implémentation précédente est peu satisfaisante, en particulier parce qu'elle utilise un autre type de structure
linéaire et aussi parce qu'à travers les attributs crées, la structure d'une liste simplement chaînée n'est pas
apparente.
À travers les exercices suivants, créons donc une autre classe ListeCh en programmation objet de manière
plus satisfaisante.
Pour simplifier, nous associerons directement la clé d'un élément de cette liste simplement chaînée à sa valeur.
Le but de cet exercice est de créer une classe Element dont chaque instance correspond
à un élément d'une liste simplement chaînée.
-
Créer cette classe avec son constructeur de sorte qu'un objet de cette classe possède deux attributs :
-
clequi correspond à la valeur de cet élément, -
pointeurqui correspond au successeur de de cet élément.
Nonesera la valeur donnée par défaut à chacun de ces attributs. -
-
Rajouter une méthode
estVidequi renvoie un booléenTruesi cet élément de liste chaînée est vide etFalsesinon. -
Rajouter la méthode
__str__suivante afin de tester la classe créée et pour mieux visualiser chaque instance :def __str__(self): """permet de visualiser un élément. """ if not self.estVide(): if self.pointeur == None: ch = "(" + str(self.cle) + "|NIL)." return ch else: ch = "(" + str(self.cle) + "|-->" + str(self.pointeur) + ")...>" return ch
Voici le début d'une classe ListeSpChainee implémentant la structure linéaire de liste simplement
chaînée :
class ListeSpChainee:
"""définition de l’objet liste simplement chaînée comme juxtaposition d'éléments de la classe Element"""
def __init__(self, debut):
"""création d'une liste simplement chaînée vide par défaut
sauf si debut est une instance non vide de la classe Element"""
if debut == None or not isinstance(debut, Element):
print("Le paramètre donné au constructeur doit être None ou une instance de la classe Element")
print("Par défaut, il y a création d'une liste simplement chaînée vide")
self.tete = Element(None)
else:
if debut.cle is not None:
self.tete = Element(debut)
else:
self.tete = Element(None) -
Créer une méthode
lstVidequi renvoieTruesi la liste simplement chaînée est vide,Falsesinon.Comme chaque élément d'un objet de la classe
ListeSpChaineeest une instance de la classeElement, il suffit d'utiliser une méthode créée sur cette classe à l'exercice précédent. -
Créer une méthode
ajouterEltEnFinqui prend en argument une valeur, qui crée un objet de typeElementayant commeclecette valeur et qui rajoute cet élément en fin de la liste sur laquelle s'applique cette méthode.-
Penser à traiter le cas où la liste est initialement vide,
-
Penser à gérer le pointeur du dernier élément de la liste initiale.
-
-
Rajouter la méthode
__str__suivante afin de tester la classe créée et pour mieux visualiser chaque instance :def __str__(self): ch = "" if not self.lstVide(): lecteur = self.tete # position de l'élément regardé (on commence toujours par la tête pour une liste simplement chaînée) while lecteur.pointeur != None: ch += "(" + str(lecteur.cle) + "|-->" + str(lecteur.pointeur.cle) + ")...>" lecteur = lecteur.pointeur # on passe à l'élément suivant. ch += "(" + str(lecteur.cle) + "|NIL)." return ch
-
Rajouter à la classe précédente
ListeSpChaineeune méthodeget_tetequi renvoie l'élément en tête de l'objet si celui n'est pas vide. -
Rajouter à cette classe
ListeSpChaineeune méthodesuccqui prend en argument une valeurelt, qui cherche dans la liste chaînée l'élément contenant cette valeur et renvoie le successeur de cette valeur dans le cas où un tel élément a été trouvé.
Penser à afficher des messages d'erreurs dans les cas où l'élément n'a pas été trouvé.
Rajouter à la classe précédente ListeSpChainee une méthode inserer qui
prend comme premier argument une valeur (à insérer comme élément) et un second argument
qui correspond à la clé de l'élément de la liste après lequel doit
s'insérer cette valeur.
Rajouter à la classe précédente ListeSpChainee une méthode supprimer qui
prend comme premier argument une valeur qui correspond à la clé de l'élément de la liste qui doit être supprimé.
Dans le cas où cet élément n'existe pas dans la liste, penser à afficher des messages d'erreurs clairs.
S'aider du pseudo-code de l'exercice 2 de ce chapitre.
Voici un exercice à faire en autonomie pour tester votre maîtrise de l'utilisation
de listes simplement chaînées implémentées par programmation objet sur
un problème concret illustrant un algorithme informatique.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Ne pas hésiter à chercher à compléter la version à trous.
Voici un exercice à faire en autonomie pour tester votre maîtrise de l'écriture et l'utilisation
de listes simplement chaînées implémentées par programmation objet sur
un problème concret.
Cet exercice est issu du site collaboratif de la forge.
Les dictionnaires
Dictionnaires
Un dictionnaire est une structure de données qui permet d'associer une valeur à une clé. Cette clé peut être un mot ou un entier. l'ensemble clé-valeur est appelé entrée.
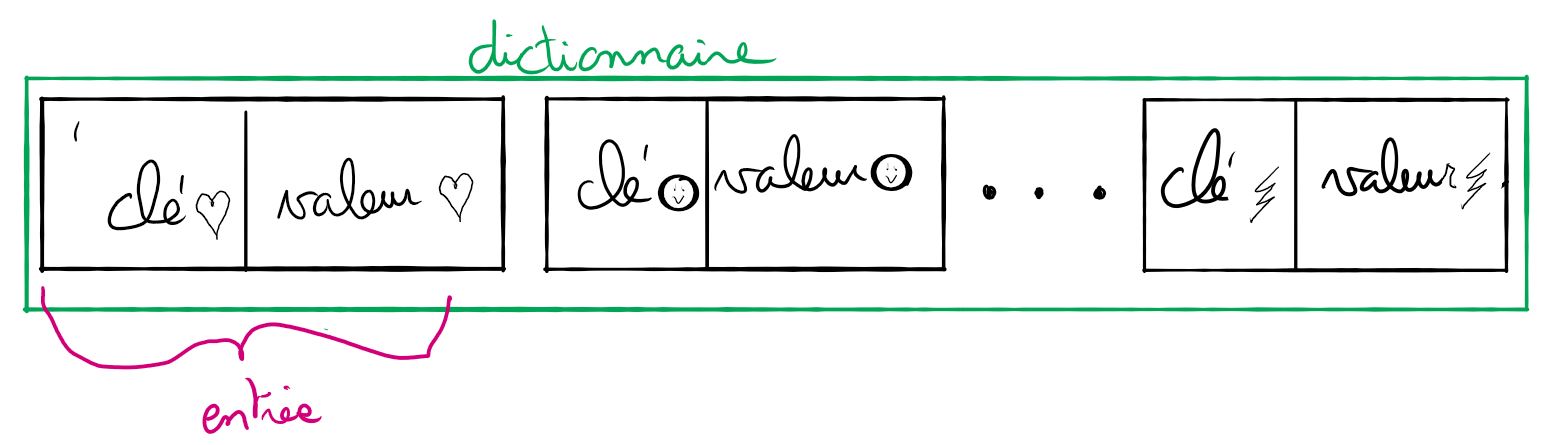
On peut modéliser un individu d'un répertoire téléphonique avec un dictionnaire. On pourrait prendre comme clés : nom et téléphone.
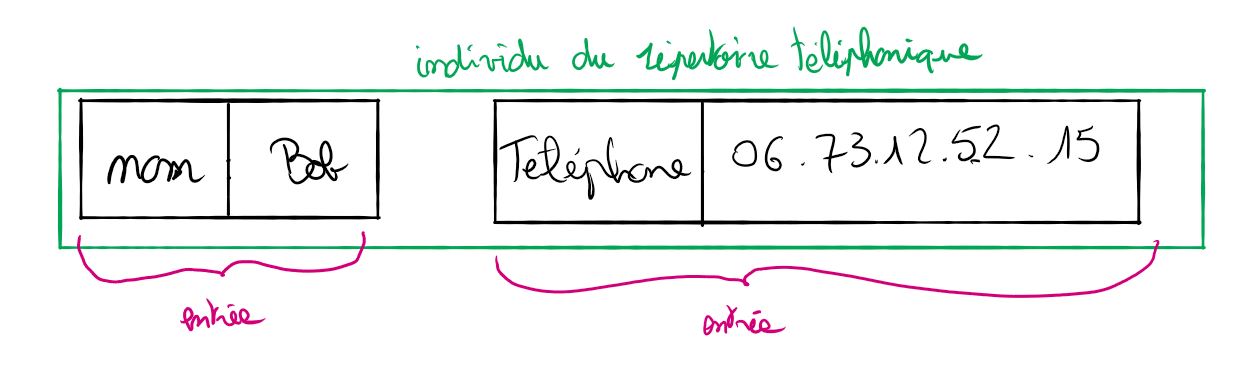
Rendez vous sur le cours de première pour retravailler l'ensemble des notions concernant les dictionnaires en Python.
Un enseignant de NSI stocke les résultats de ses élèves à l'aide d'un dictionnaire :
-
les clés sont les noms des élèves,
-
les valeurs sont des dictionnaires dont les clés sont les noms des épreuves et les valeurs sont des listes contenant la note obtenue suivie du coefficient de l'épreuve.
Voici le dictionnaire de 3 de ses élèves :
resultats = {'Alice': {'DS1' : [15.5, 3],
'DM1' : [14.5, 1],
'DS2' : [17, 4],
'PROJET1' : [18, 5],
'DS3' : [16, 4]},
'Bob':{'DS1' : [6 , 3],
'DM1' : [14.5, 1],
'DS2' : [8.8, 4],
'PROJET1' : [10, 5],
'IE1' : [7, 2],
'DS3' : [8, 4],
'DS4' :[10, 4]},
'Chaïn':{'DS1' : [13.5, 3],
'DM1' : [16, 1],
'DS2' : [14.5, 4],
'PROJET1' : [16, 5],
'IE1' : [16, 2],
'DS4' : [19, 4]}}
Le problème est que le professeur n'arrive pas à créer une fonction moyenne prenant en paramètre
le dictionnaire resultat ainsi qu'un nom sous forme de chaîne de caractères et qui renvoie
la moyenne des notes de l'élève ayant ce nom nom dans le cas où son nom apparaît dans le
dictionnaire resultat.
Proposer une telle fonction moyenne afin d'aider cet enseignant. Il en sera sûrement reconnaissant !
Voici un exercice à faire en autonomie pour tester votre maîtrise des dictionnaires.
Cet exercice est issu du site collaboratif de la forge.
Comme l'exercice précédent, cet exercice est proche d'un exercice de l'Épreuve pratique de l'an dernier.
Cliquer sur ce lien pour accéder à l'exercice.
Ne pas hésiter à surtout chercher à compléter la version à trous, celle proche d'un exercice 2 de l'Épreuve Pratique.
Exercices
Préciser quelle est la structure de données à privilégier pour chacune de ces tâches :
-
Représenter un répertoire téléphonique.
-
Stocker l'historique des actions effectuées dans un logiciel et disposer d'une commande Annuler.
-
Envoyer des fichiers au serveur impression.
-
On souhaite stocker un texte très long que l'on souhaite pouvoir modifier.
Dans chacun des cas suivants, déterminez quelle structure de données est la plus adaptée :
-
Gérer le flux des personnes arrivant à la caisse d'allocations familiales.
-
Mise en place d'un mécanisme annuler/refaire pour un traitement de texte.
-
Garder les nombres premiers parmi les nombres de 2 à 1000 en utilisant la méthode du crible d'Ératosthène.
-
Lors d'une partie échec, on veut enregistrer l'ensemble des coups joués et pouvoir les consulter.
-
Que signifie l'acronyme "FIFO" ?
À quelle structure de données correspond cet acronyme ? -
Que signifie l'acronyme "LIFO" ?
À quelle structure de données correspond cet acronyme ?
Une usine européenne fabrique des voitures.
Chaque véhicule en cours de fabrication ou terminé possède
un numéro de série pour l'identifier.
-
Quelle structure de données est à privilégier pour gérer les véhicules sur la chaîne de production sur laquelle les portes sont fixées à la carrosserie ?
-
Quelle structure de données est à privilégier pour gérer le lien entre le numéro de série du véhicule terminé avec l'ensemble de ces caractéristiques ?
-
Les véhicules de luxe terminé sont stockés avant envoi dans des longs hangars étroits cul à cul.
Sachant que ces hangars ne possèdent qu'une seule porte d'entrée à véhicule, quelle est la structure de données à privilégier pour gérer l'entrepôt de ces véhicules ? -
L'entreprise travaille avec de nombreux sous-traitants européens.
Quelle structure de données est à privilégier pour gérer l'ensemble des noms sous-traitants européens ? -
Pour communiquer avec une entreprise sensible se trouvant aussi dans l'Union Européenne, l'entreprise vérifie toutes les minutes le routage des paquets entre elle et cette entreprise afin de s'assurer de ne passer que par des routeurs au sein de l'Europe.
Quelle structure de données est à privilégier afin de gérer chaque minute l'ensemble des routeurs par lesquels semblent transiter les paquets transmis ?
La pile et la poo
Voilà une définition de la classe pile en Python :
class Pile:
def __init__(self, haut, reste=None):
self.h = haut
self.r = reste
def estVide(self):
if self.h == None:
return True
else:
return False
def empiler(self, valeur):
self.r = Pile(self.h, self.r)
self.h = valeur
def depiler(self):
if self.r == None:
haut = self.h
self.h = None
return haut
else:
haut = self.h
self.h = self.r.h
self.r = self.r.r
return haut
def affiche(self):
if self.r == None:
print(self.h)
else:
Pile.affiche(self.r)
print(self.h)On considère la pile : P=("bob", (3, ("nsi", (5, ("vacances", vide))))) .
-
Expliquer comment est implémentée la fonction
empiler. -
Expliquer comment est implémentée la fonction
depiler. -
Créer une pile vide et tester qu'elle est bien considérée comme vide.
-
Implémenter
Psur votre machine en utilisant les méthodes (constructeurs et modificateurs) de la classePile. -
Améliorer la méthode
affichepour quelle affiche la pile dans le bon sens. -
Écrire une méthode
hauteurqui renvoie la hauteur de la pile. -
Écrire une méthode
depil2qui enlève de la Pile sur laquelle s'applique la méthode l'élément situé en deuxième position de la pile et renvoie cet élément. -
Écrire une fonction
insere(P, elt)qui insère dans une pilePl'élémenteltà la position 2. On considère la position 1 correspond au haut de la pile. -
Écrire une fonction
acces(P, pos)qui renvoie l'élément situé en positionpos.
L'objet file en Python
Voila une définition de l'objet file en Python (implémenté avec une liste doublement chaînées)
On commence par définir un élément d'une liste doublement chaînées :
class Element:
# chaque élément a pour attribut : le précèdent , le suivant et la valeur de l'élément
def __init__(self, x):
self.val = x
self.precedent = None
self.suivant = None
def __str__(self): # méthode qui permet de lance un print sur un tel objet
return str(self.val) + "-" + str(self.suivant)on définit ensuite l'objet file :
class File:
#ici une file est la donnée de deux attributs : la file complète de type Element et le dernier élément de la file de type Element
def __init__(self):
self.tete = None
self.queue = None
def enfile(self, x):
e = Element(x) # on transforme l'élément à ajouter en un objet Element de listes doublement chaînées
if self.tete == None:
self.tete = e # file vide la tete est remplacée par l'élément e
else:
e.precedent = self.queue #le précédent de l'élément pointe sur l'ancienne queue de la file
self.queue.suivant = e #l'ancienne queue de la file pointe sur e avec suivant
self.queue = e #on redéfinit self.queue par e.
def file_vide(self):
return self.tete is None #renvoie True si None et False sinon
def defile(self):
if not self.file_vide():
e = self.tete #on stocke l'élément à defiler
if e.suivant is None: #cas où il n'y a qu'un élément
self.tete = None
self.queue = None
else:
self.tete = e.suivant
self.tete.precedent = None
return e.val
def __str__(self):
return str(self.tete)Voici une vidéo pour vous aider à comprendre les deux classes ci-dessus ainsi que la notion de liste doublement chaînée :
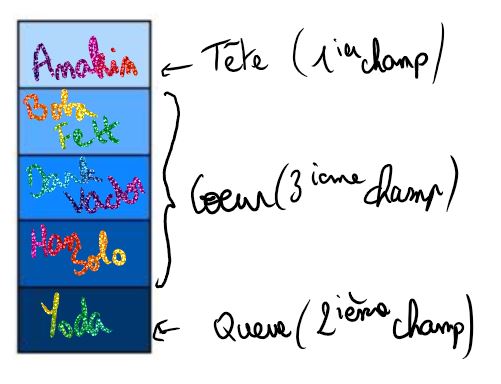
On considère la file : F = (5, 11115, ("vacances", "Bob", 7, "nsi", 12)).
Revoir l'implémentation de la file vue au cours sd1 en cas de besoin
-
Identifier, dans l'exemple, la tête, la queue et le cœur de
F. -
Créer une file vide et tester qu'elle est bien considérée comme vide.
-
Implémenter
Fsur votre machine en utilisant les méthodes (constructeurs et modificateurs) de la classeFile. -
Écrire une fonction
longueur(F)qui renvoie la longueur de la file. -
Écrire une procédure
affiche_coeur(F)qui affiche le cœur de la file.
Exercices du Baccalauréat
Demander le programme !
-
La notion de structure de données linéaire.
-
La notion de type abstrait liste.
-
La notion de tableau dynamique.
-
La notion de type abstrait liste simplement chaînée.
-
La notion de dictionnaire.
-
La notion de pile.
-
La notion de file.
-
Écrire en pseudo-code une fonction nouvelle en utilisant des fonctions données comme interface d'un type abstrait.
-
Utiliser les méthodes sur les listes.
-
Utiliser les méthodes sur les dictionnaires.
-
Déterminer la structure de données la plus appropriée à une tâche donnée.
-
Compléter l'implémentation d'une structure données utilisant la programmation orientée objet.
-
Distinguer des structures (comme pile, file, liste, ...) à partir des méthodes qui caractérisent leur interface.
-
Distinguer la recherche d'une valeur dans une liste et dans un dictionnaire.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International