Programmation dynamique

Demandez le programme

Retour sur la suite de Fibonacci

Nous avons étudié en début d'année dans le chapitre sur la récursivité un exercice historique modélisant l'évolution d'une population de lapins immortels.
Le nombre de lapins au bout de $n$ mois, est noté $Fibo(n)$ avec comme hypothèses : $\begin{equation} Fibo(n)=\begin{cases} 1 &, \text{si $n=0$}.\\ 1 &, \text{si $n=1$}.\\ Fibo(n-1) + Fibo(n-2) &, \text{si $n>1$}. \end{cases} \end{equation}$

À cette occasion, vous aviez créé la fonction récursive Fibo suivante :

def Fibo(n: int) -> int:
    if n==0 or n==1:
        return 1                       
    else:
        return Fibo(n-1)+Fibo(n-2)

Nous avions vu que cette fonction était très peu performante, par exemple le calcul de Fibo(35) demande d'être assez patient.

Voici le graphe des appels récursifs nécessaires pour calculer Fibo(5) :

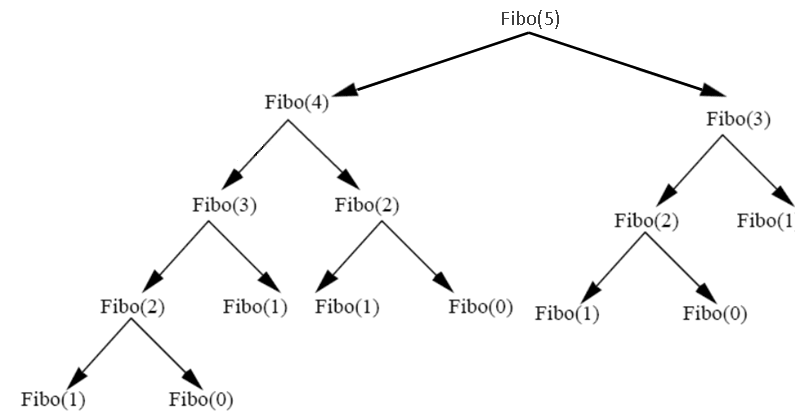
On peut comprendre le temps d'exécution important par le fait que plusieurs appels sont redondants :

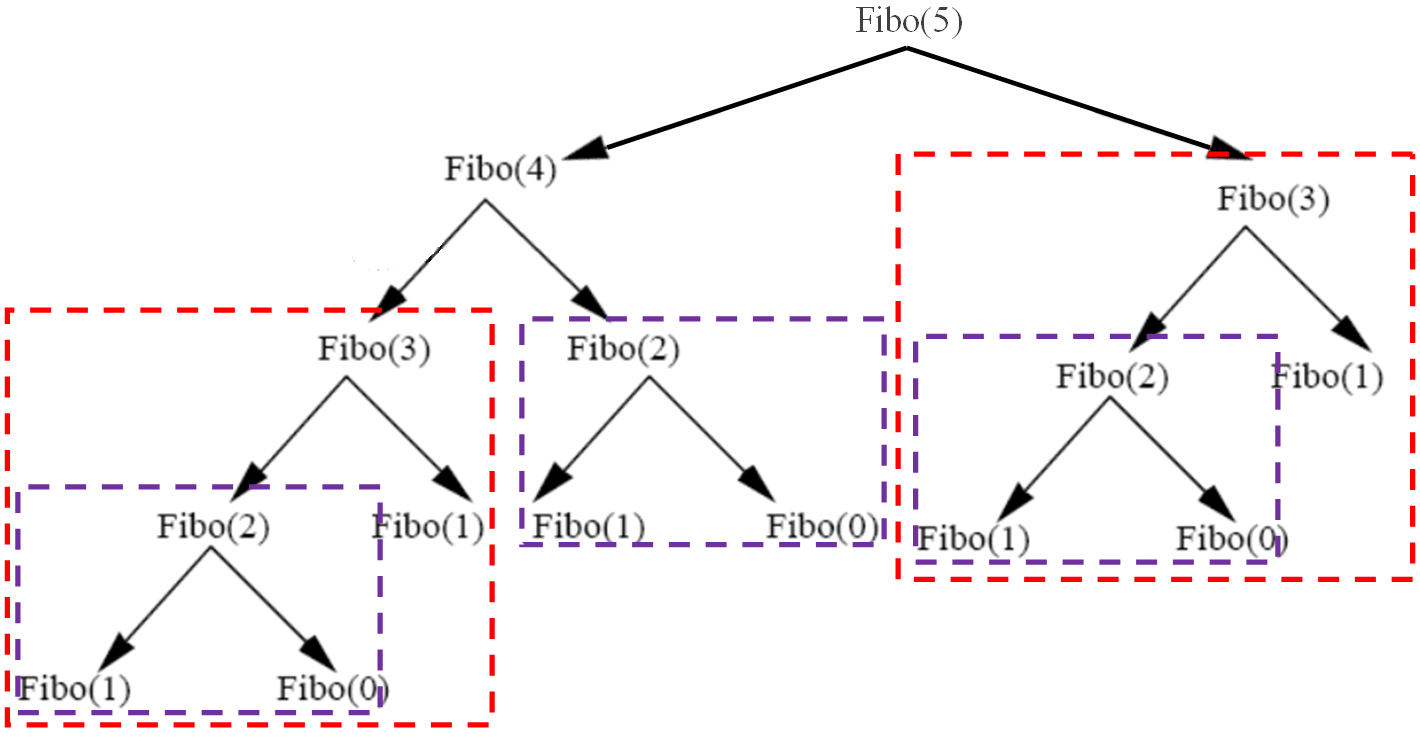
Il est donc possible d'améliorer l'algorithme pour éviter ces calculs redondants en mémorisant les résultats précédents en utilisant un tableau.
De plus, l'utilisation de ce tableau va permettre de transformer cet algorithme récursif en un itératif : il suffit de changer l'ordre de parcours ; au lieu de diminuer de $n$ à 1 et 0 comme dans l'algorithme récursif, il suffit d'augmenter dans le tableau de 0 et 1 à $n$.

Créer une fonction (itérative) Fibo_iter :

qui prend en paramètre un entier naturel $n$,
qui teste que le paramètre saisi est bien de type entier et est positif,
qui utilise un tableau implémenté par une liste dans laquelle seront stockés les valeurs successivement calculées en utilisant le fait que les deux premières valeurs sont égales à 1 et que l'on obtient une nouvelle valeur en additionnant les deux valeurs la précédant puisque : $\begin{equation} Fibo(n)=\begin{cases} 1 &, \text{si $n=0$}.\\ 1 &, \text{si $n=1$}.\\ Fibo(n-1) + Fibo(n-2) &, \text{si $n>1$}. \end{cases} \end{equation}$
qui renvoie la valeur de $Fibo(n)$.

On admet que le coût en temps de la fonction récursive Fibo est exponentiel.

Déterminer le coût en temps de la fonction itérative Fibo_iter.

La programmation dynamique est une stratégie visant à éliminer les calculs redondants. À l’origine elle s’applique à des problèmes d’optimisation.
On peut la voir comme une méthode algorithmique qui consiste à résoudre un problème :

en le décomposant en sous-problèmes,
puis à résoudre les sous-problèmes, des plus petits aux plus grands,
en mémorisant les résultats intermédiaires.

Le coût en temps de calcul est donc réduit en augmentant le coût en mémoire.
Cette technique qui vise à réduire le temps de d'exécution d'une programme en mémorisant des valeurs est appelée mémoïsation, terme issu d'un anglicisme.

Cette méthode a été introduite au début des années 1950 par Richard Bellman dans le cadre de travaux en mathématiques appliquées.
Ce nom de programmation dynamique a été donné alors. Il est important de bien comprendre que ”programmation” dans ”programmation dynamique”, ne doit pas s’entendre comme "utilisation d’un langage de programmation", mais comme synonyme de planification et ordonnancement

Dans cet exemple, vous venez de découvrir les éléments essentiels de la programmation dynamique :

l'écriture d'un algorithme récursif naïf (donné au début dans cet exemple) afin de résoudre d'abord les cas simples (ceux de la condtion d'arrêt) pour pouvoir traiter ensuite les cas plus compliqués.
utiliser un tableau servant à mémoriser les résultats déjà calculés pour ne pas les recalculer afin de réduire le coût en temps de calcul,
transformer un algorithme récursif et en itératif en raisonnant dans l'ordre inverse de celui des appels récursifs afin de finir l'optimisation. (élément effectué en même temps que le précédent dans cet exemple).

Vous allez mettre en oeuvre cette démarche dans l'exemple suivant et découvrir toute sa force.

Exemple introduisant la démarche générale

Présentation d'un jeu

Le jeu est constitué d'un plateau formé d'un graphe en forme de pyramide de hauteur $n$ où à chaque sommet sont déposés des points : un nombre entre 1 et 9.
Chaque joueur joue sur le même plateau indépendamment des choix des autres. À chaque sommet, tout joueur ajoute à son score le nombre de points correspondant au sommet puis doit choisir de partir vers un des deux sommets enfants.
À l'issue des $n$ sommets visités sur toute la hauteur du graphe pyramidal, le joueur ayant cumulé le plus de points est déclaré vainqueur.
Quelle stratégie mettre en oeuvre afin de gagner à coup sûr ?

Deux joueurs, nommés "Rouge" et "Bleu", s'affrontent sur un plateau formé du graphe pyramidal de hauteur $n=4$.
Le gagnant est celui obtenant la somme la plus grande.

Voici ci-dessous les choix successifs opérés par ces deux joueurs.

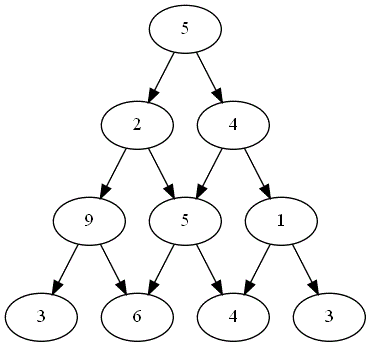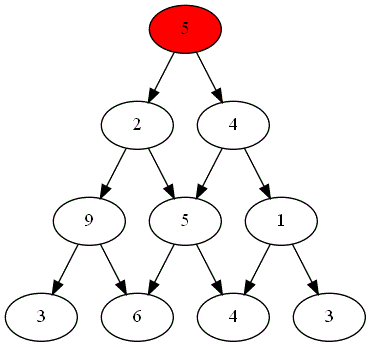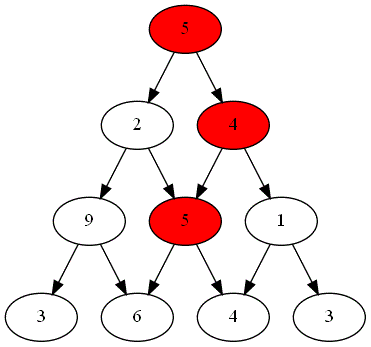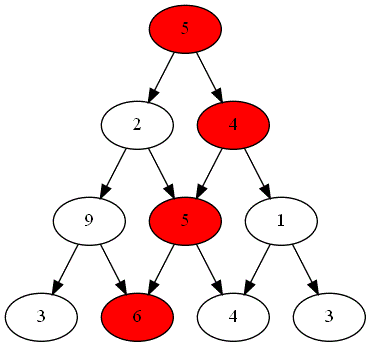
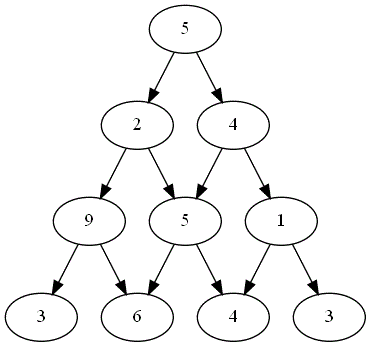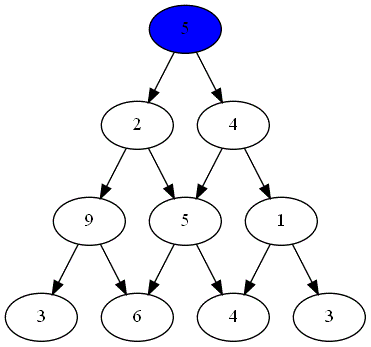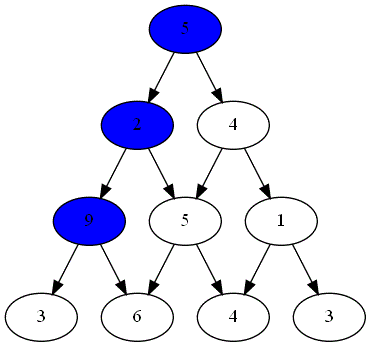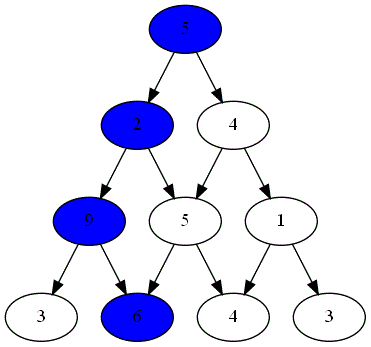
Quel est le joueur gagnant ?
Le parcours choisi par le joueur gagnant est-il optimal ?

Stratégie exhaustive : calculer tous les cas possibles

Afin d'être sûr de gagner à ce jeu, un joueur décide de programmer le calcul de tous les cas possibles pour en déduire quels choix il doit successivement faire. On appelera dans l'exercice suivant cettte stratégie comme stratégie exhaustive.

Lorsque le plateau de plateau formé d'un graphe pyramidal de hauteur 1 ou 2, comme dans cet exemple 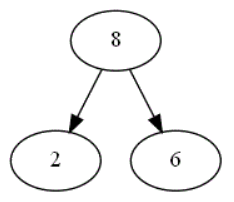, combien de chemins différents existent dans ce graphe pyramidal en partant du sommet 8, chemins correspondant aux différents choix possibles lors d'une partie ?
On considère ce plateau formé d'un graphe pyramidal de hauteur 3 :
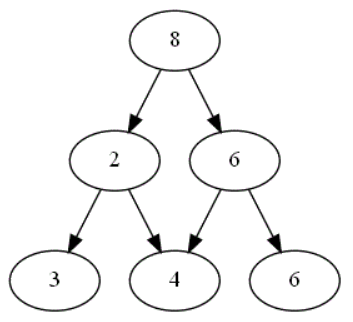
Combien de chemins différents existent-ils dans ce graphe pyramidal en partant du sommet 8, chemins correspondant aux différents choix possibles lors d'une partie ?
On considère ce plateau formé d'un graphe pyramidal de hauteur 5 :
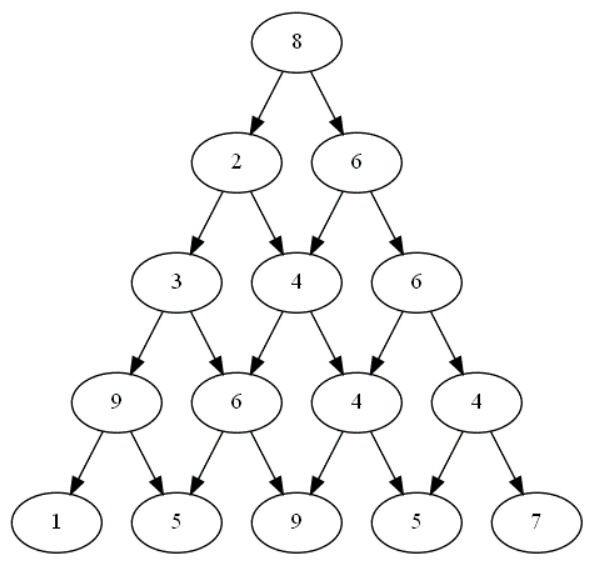
Combien de chemins différents existent-ils dans ce graphe pyramidal en partant du sommet 8, chemins correspondant aux différents choix possibles lors d'une partie ?
Plus généralement, on considère un plateau formé d'un graphe pyramidal de hauteur $n$.
Combien de choix différents sont possibles lors d'une partie pour un joueur donné ?
L'ordre de grandeur du coût en opérations (=complexité) de cette stratégie exhaustive appliquée à un graphe pyramidal de hauteur $n$ sera-t-elle plutôt constante ? Linéaire ? Quadratique ? Polynomiale ? Exponentielle ?
Qu'en déduire quant à la faisabilité de cette stratégie sachant que le plateau peut atteindre une hauteur de 50 ?

Pour modéliser ce problème en Python, il y a plusieurs manières (dictionnaire implémentant un graphe, liste des listes de nombres rencontrés sur une ligne, ...). Dans la suite, on modélisera le plateau de jeu comme liste des listes de nombres rencontrés sur une ligne.

Le plateau de jeu suivant 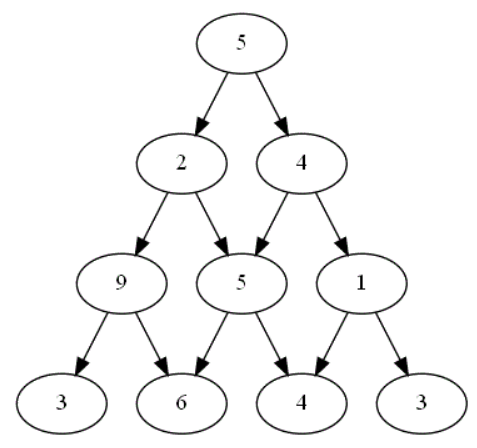est modélisé la liste suivante :

plateau = [[5], [2,4], [9,5,1], [3,6,4,3]]

Proposer une fonction construire_plateau qui prend en paramètre un entier naturel non nul $n$ qui correspond à la hauteur du graphe pyramidal représentant le plateau de jeu et qui renvoie une liste de listes correspondant à un graphe pyramidal de hauteur $n$ dont les valeurs sont des nombres entiers aléatoires compris entre 1 et 9.

Importer la fonction randint du module random pour obtenir un nombre entier aléatoire entre deux bornes.

Le but est d'obtenir un visuel simplifié du plateau de jeu dans la partie console : le graphe sera affiché (sans flèche) en mode texte comme une pyramide de nombres superposés.
Ainsi, le plateau 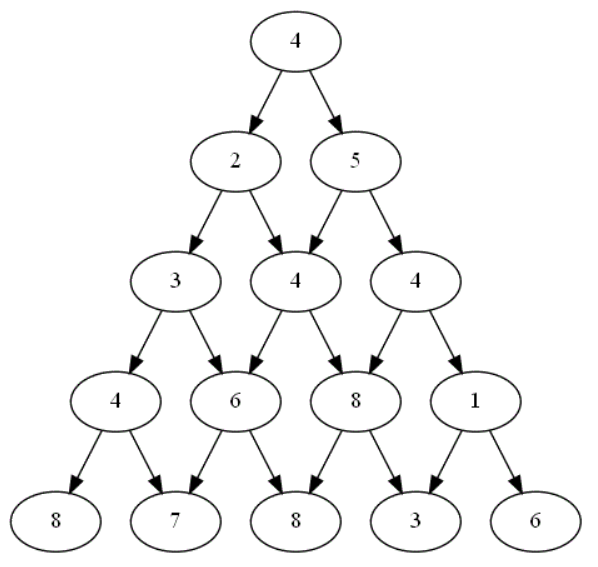sera affiché en console sous cette forme :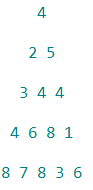

Proposer une procédure afficher_plateau qui prend en paramètre un plateau de jeu implémenté sous forme d'une liste de listes et qui affiche en mode texte le plateau de jeu comme une pyramide de nombres superposés.

Chaque nombre aléatoire prendra la place d'une case, tout comme chaque espace séparant deux nombres d'une même ligne.
Vous pouvez utiliser l'attribut end de l'instruction print.

Stratégie coup par coup

Le joueur décide de mettre en place une autre stratégie : à chaque sommet, il choisit de choisir comme suivant celui ayant la plus forte valeur.
Dans la suite, on appelle cette stratégie stratégie coup par coup.

Comment s'appelle le type d'algorithme modélisant cette stratégie ?

Appliquer la stratégie coup par coup au plateau de jeu suivant :
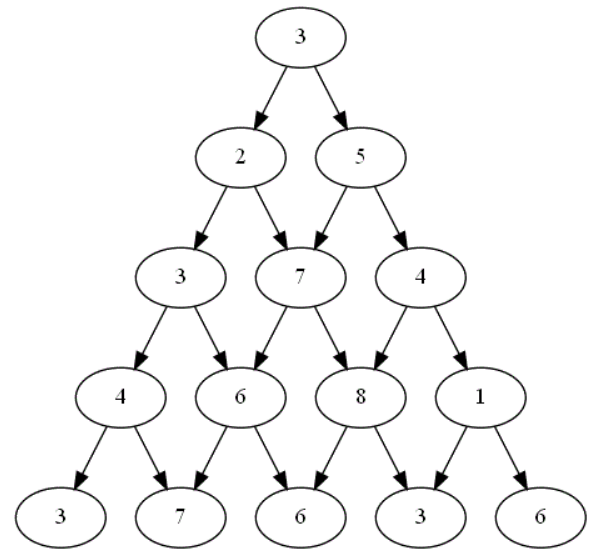
Déterminer le nombre de comparaisons à faire par le joueur appliquant cette stratégie sur ce plateau particulier ?
On suppose ici que chaque addition, comparaison et accès à la mémoire coûte une opération.
Quel est l'ordre de grandeur du coût en opérations (=complexité) de cette stratégie coup par coup appliquée à un graphe pyramidal de hauteur $n$ ?

Proposer une fonction strateg_glouton qui prend en paramètre un plateau de jeu implémenté comme liste de listes, qui à chaque étape détermine le sommet permettant de maximiser la somme parmi les deux possibles et qui renvoie le tuple formé de la liste des sommets à choisir successivement et de la somme totale obtenue.
Tester votre fonction en utilisant le plateau de jeu correspondant à l'exercice précédent.

Voici un plateau de jeu possible :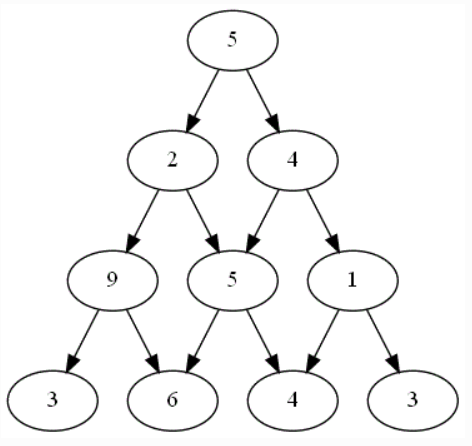

Appliquer la stratégie coup par coup à ce plateau.
Que pensez-vous quant à la pertinence de cette stratégie ?

Vers une stratégie efficace

La stratégie exhaustive permet de trouver la meilleure succession de choix à faire afin de maximiser la somme finale mais elle est informatiquement non pertinente du fait de son coût exponentiel.

L'idée ici va être d'étudier plus finement cette stratégie pour ensuite chercher un moyen de réduire le coût de sa mise en oeuvre.

L'idée de la méthode gloutonne est d'obtenir un algorithme itératif qui optimise le choix sur une profondeur d'une seule ligne.
Pour améliorer cette méthode gloutonne ne donnant pas forcément la solution optimale, il faut regarder toute la suite des lignes, comme le fait la méthode exhautive. De plus une vision récursive peut sembler plus simple à élaborer initialement.

Pour faciliter la modélisation sous forme récursive, nous noterons :

$l$ le numéro de la ligne du plateau de jeu en partant du haut (en commençant à 0). Forcément $0\le l\le n-1$, où $n$ est la hauteur du graphe pyramidal représentant le plateau.
Sur une ligne $l$ donnée, les éléments sont numérotées à partir de 0. On note $k$ la variable donnant leur position sur cette ligne. Forcément, $0\le k\le l$.
une liste de listes nommée plateau stocke l'ensemble des valeurs du plateau de jeu.
Le nombre de la ligne $l$ et de la colonne $k$ correspond à l'élément plateau[l][k]. Voici une représentation visuelle dans le cas où $n=6$ :

Le but est de construire une fonction récursive max_rec qui prend en paramètre une liste de listes implémentant le plateau de jeu ainsi que deux nombres entiers $l$ et $k$ correspondant à une ligne du plateau de jeu et à une colonne de cette ligne et qui renvoie la somme maximale que l'on peut obtenir en descendant dans pyramide à partir du sommet se trouvant sur la ligne $l$ à la colonne $k$.

Que doit renvoyer max_rec(plateau, l, k) lorsque $l = n-1$, c'est-à-dire lorsque l'on considère un sommet de la dernière ligne du plateau ?
Quel lien existe-t-il entre max_rec(plateau, l, k) avec max_rec(plateau, l+1, k) et max_rec(plateau, l+1, k+1) ?

Aidez-vous des schémas ci-dessous, dans le cas où $l=1$ et $k=0$ pour trouver la relation entre max_rec(plateau, l, k), la somme maximale du plateau triangulaire rouge en fonction de la valeur plateau[l][k], entourée en rouge, max_rec(plateau, l+1, k), la somme maximale du plateau triangulaire réduit bordeaux et max_rec(plateau, l+1, k+1), la somme maximale du plateau triangulaire réduit violet :
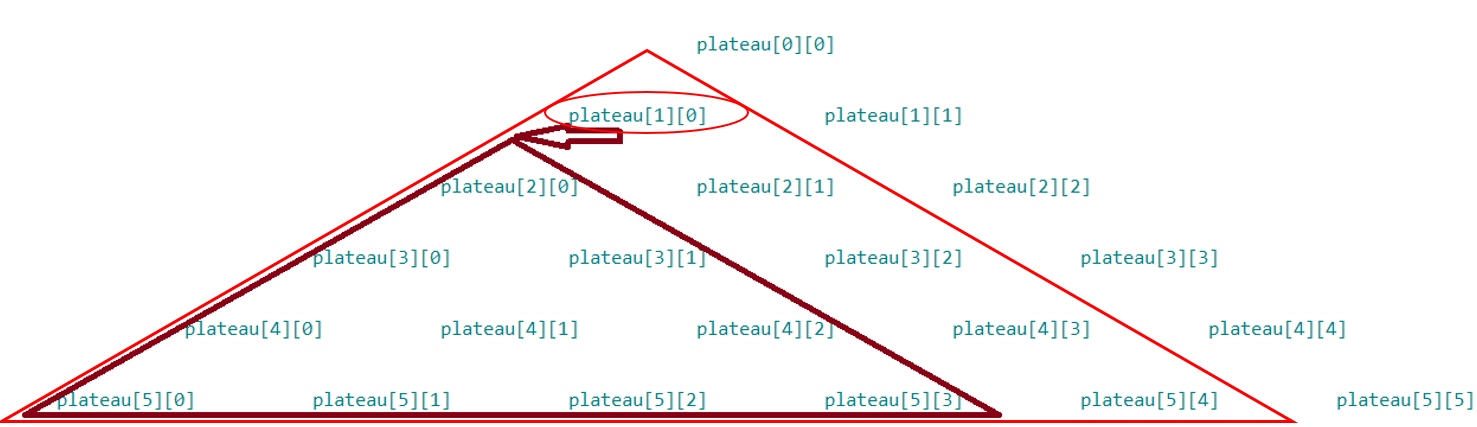
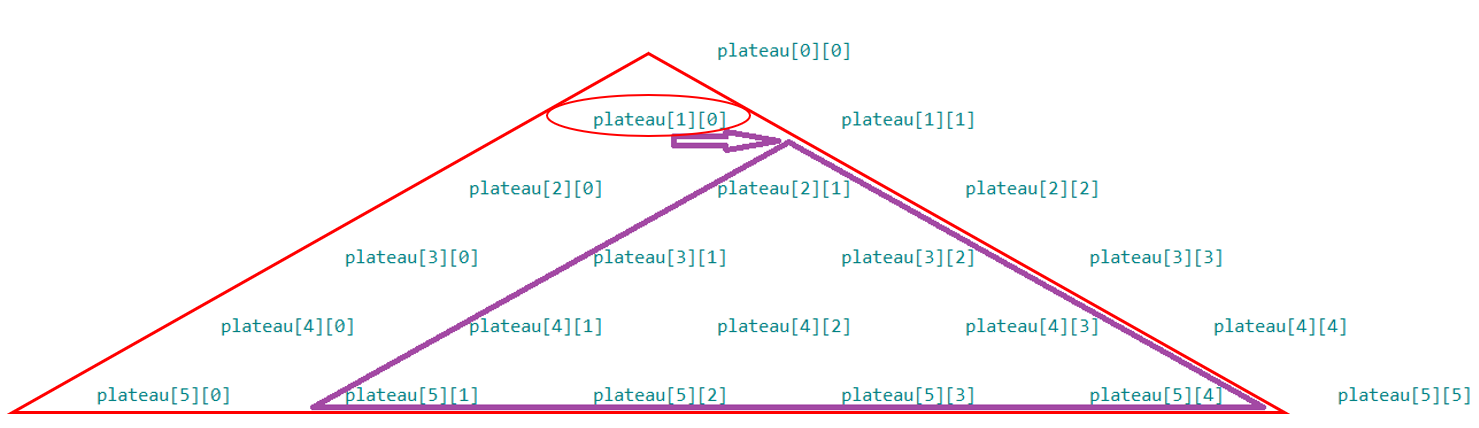
En déduire l'écriture de la fonction récursive max_rec.
Quel appel de max_rec permet de savoir quelle est la somme maximale que l'on peut obtenir avec le plateau de jeu plateau ?
Tester votre fonction avec un des plateaux déjà étudiés dans des exercices précédents.

On peut visualiser la démarche récursive précédente comme une démarche "bottom-up" : on part de la base de la "pyramide" correspondant au plateau de jeu pour aboutir au sommet de celle-ci : le point de départ du jeu.

Pour simplifier, considérons un plateau de hauteur 4 :

Supposons que l'on exécute max_rec(plateau, 0, 0) sur ce plateau de hauteur 4.
La fonction étant récursive, max_rec(plateau, 0, 0) va conduire à l'appel de max_rec(plateau,1,0) et max_rec(plateau, 1, 1),
de même, max_rec(plateau, 1, 1) va conduire à l'appel de max_rec(plateau, 2, 1) et max_rec(plateau, 2, 2),
de même, max_rec(plateau, 2, 1) va conduire à l'appel de max_rec(plateau, 3, 1) et max_rec(plateau, 3, 2),
seuls les appels liés à la dernière ligne du tableau comme max_rec(plateau, 3, 1) renvoie directement un résultat sans nouvel appel.
Voici une représentation des différents appels récursifs liée à l'exécution de max_rec(plateau, 0, 0) (l'ordre d'apparition dans la pile d'exécution n'étant pas respecté) :

On peut démontrer plus généralement que pour un graphe pyramidal de hauteur $n\ge 1$, l'appel max_rec(plateau, 0, 0) conduit à $2^{n}-2$ appels récursifs.

On peut aussi démontrer que votre fonction max_rec écrite précédemment est de complexité exponentielle de la forme $O(2^n)$ comme l'algorithme itératif naïf exhaustif étudié précédemment.

Calculer le nombre de sommets d'une pyramide de hauteur $n$.
De combien de résultats différents pourrait-on se contenter au minimum pour déterminer le meilleur parcours.
Comment expliquer un tel écart entre le nombre réel d'appels récursifs obtenu et celui suffisant de résultats différents ?

On effectue donc plusieurs fois le même appel comme l'illustre cette représentation des appels effectués :

Ces appels redondants font recalculer plusieurs fois la même valeur donc une idée pour réduire le coût est de stocker dans un "tableau" les valeurs déjà calculées.

Un tableau stock aura toutes ses valeurs initialisée à 0 (cette valeur est une sentinelle : elle permet de savoir si une valeur a déjà été calculée ou pas : 0 signifie que la valeur n'a pas été calculée tandis qu'un calcul de somme maximum conduit à un nombre valant au moins 1)

Quelle structure utiliser pour stock afin de faciliter sa gestion dans le programme ?
Que contiendra la variable x à la suite de l'instruction x = [0]*8 ?

Voici ci-dessous un script incomplet donnant une fonction max_rec_memoire qui correspond à la fonction récursive précédente max_rec dans laquelle une utilise le tableau stock comme variable globale.

(vous pouvez retrouver des informations sur les variables globales dans ce cours de première ou dans ce chapitre sur Boyer-Moore )

Compléter ce script (au niveau des ... ) :

# Création et initialisation de la variable stock
stock = []
for ligne in plateau:
    lig_stock = [0]*len(ligne)
    stock.append(lig_stock)

def max_rec_memoire(plateau:list, l:int, k:int)->int:
    """ fonction récursive qui prend en paramètre :
        plateau est une liste de sous-listes, chacune des sous-listes
    représente une ligne de la pyramide formant le plateau.
        l est le numéro d'une ligne de ce plateau
        k est le numéro donnant la position d'un élément de cette ligne l
    Cette fonction renvoie le maximum possible sur ce plateau en partant du sommet
    se trouvant ligne l en position k.
    """
    global stock          # utilisation d'une variable globale pour stocker les maxima déjà calculés
    if stock[l][k] != 0:  # valeur déjà calculée donc connue
        return ...
    else:                 # valeur demandée à calculer
        n = len(plateau)
        if l == n-1: #élément de la dernière ligne
            stock[l][k] = ...
            return ...
        else:    # cas d'un élément se trouvant au-dessus de la dernière ligne
            stock[l][k] = ...
            return ...

Tester votre fonction max_rec_memoire avec un des plateaux déjà étudiés dans des exercices précédents.

L'amélioration précédente n'est pas suffisante en particulier pour deux raisons :

L'utilisation précédente d'une variable de stockage est insuffisante pour n'avoir que $\dfrac{n(n+1)}{2}$ appels car de nombreux appels récursifs vont être effectués avant de commencer à remplir la variable stock ; ceci commence lors des appels de la dernière ligne.
Ainsi, nous n'avons pas réduit au mieux la complexité de l'algorithme.
De plus, l'utilisation de la variable stock comme variable globale est normalement à éviter.

Pour améliorer cela, l'idée est désormais de passer d'un algorithme récursif à un itératif tout en gardant l'idée d'une variable de stockage.
Pour l'itératif, plutôt que de partir de la base, l'idée est de partir directement du sommet voulu : on va désormais du haut vers le bas !

Voici un plateau de jeu :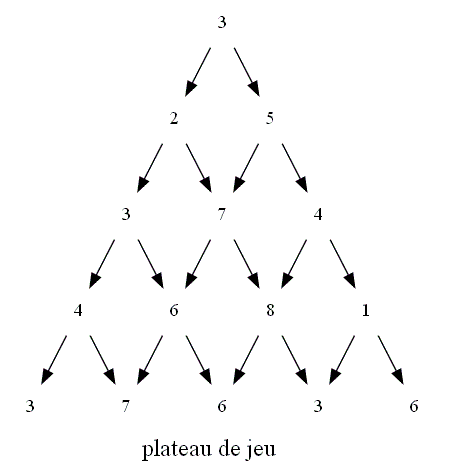

À ce plateau de jeu, on va accoler une seconde pyramide dans laquelle on stockera les maxima trouvés. Cette seconde pyramide est une illustration du tableau stock qui permettra d'optimser le programme. C'est la raison pour laquelle toutes les valeurs sont initialement à 0.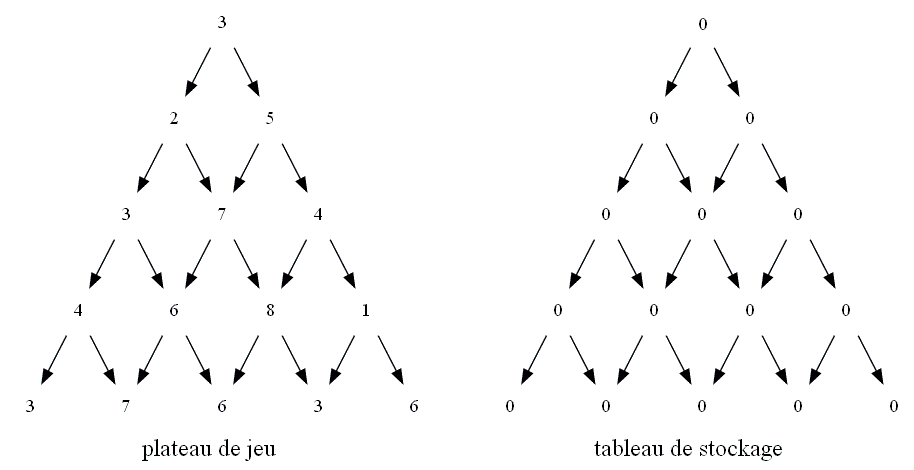

Comme on va désormais du haut vers le bas, l'élément stock[l][k] du tableau de stockage mémorisera la somme maximale que l'on avoir une fois arrivé à la k-ième case de la ligne l de la pyramide en partant du haut.

Reproduire sur une feuille cette seconde pyramide en remplaçant chaque 0 par le maximum que l'on peut avoir en chaque case en partant du sommet.

Pour passer d'un algorithme récursif à un itératif, on peut analyser l'ordre des appels (on parle d'analyse de dépendance).
Pour cela:

on dessine un graphe orienté, dit graphe de dépendance de l’algorithme récursif. Les noeuds sont étiquetés par un jeu de paramètres.
Un arc d’un noeud $a$ vers un noeud $b$ signifie que l’exécution de l’algorithme récursif avec les paramètres $b$ appelle l’algorithme avec les paramètres $a$, c’est-à-dire que "$a$ sert à $b$".
Ce graphe se superpose au tableau de mémorisation : chaque noeud correspondant à une case.

Ce graphe de dépendance est sans cycle, sinon l’algorithme récursif ne termine pas.

Sur l'image ci-dessous, rajouter des flèches afin de faire apparaître le graphe de dépendance entre les différentes cases du plateau de jeu lors des appels récursifs.
En s'aidant du sens des flèches ajoutées, devinez comment on peut dans l'algorithme itératif :
- calculer la valeur maximale pour atteindre une case se trouvant sur un bord droit ou gauche du plateau de jeu à partir d'une case parente ?
- calculer la valeur maximale pour atteindre une case se trouvant à l'intérieur du plateau de jeu à partir des cases parentes ?
Vu le nouveau sens des flèches, quelle informations doit-on désormais stocker dans la variable stock ?

Proposer une fonction (itérative) somme_max_iter_memoire qui permet de calculer la somme maximale à partir du sommet initial du plateau de jeu.
Tester votre fonction somme_max_iter_memoire avec un des plateaux déjà étudiés dans des exercices précédents.
Estimer la complexité de votre algorithme.

Bravo !
Vous avez réussi à trouver une solution algorithmique en un coût en temps bien plus faible que la solution naïve initialement trouvée !

On peut résumer en pratique la programmation dynamique mise en oeuvre dans cet exemple en la succession de trois étapes :

On commence par écrire un algorithme récursif naïf qui fait des calculs redondants.
On stocke (souvent dans un tableau) les résultats intermédiaires. On obtient un algorithme récursif avec mémorisation qui lit son résultat s’il a déjà été calculé ; qui calcule et stocke son résultat sinon.
Une analyse de l’ordre des appels (dite analyse de dépendance) permet d’écrire un algorithme itératif équivalent.

Les deux dernières étapes sont souvent faites simultanément.

Modifier le code de l'exercice précédent afin d'obtenir une fonction qui renvoie le parcours à suivre afin d'obtenir le score maximal au jeu.

Afin d'éviter toute confusion dans le cas où deux enfants ont la même valeur, le parcours renvoyé peut être une liste contenant comme élément 'D' ou 'G' pour gauche ou droite afin de préciser la direction à prendre à partir de chaque sommet parent.

Voici un résumé visuel de la mise en oeuvre de la programmation dynamique :

Commencer par écrire un algorithme récursif modélisant la situation.
En déduire un graphe de dépendance en reliant les sommets liés lors de la récursivité :
Utiliser un tableau pour stocker les valeurs calculées afin d'éviter les redondances :
En déduire un algorithme itératif répondant à la question avec un coût réduit grâce à un tableau de stockage :
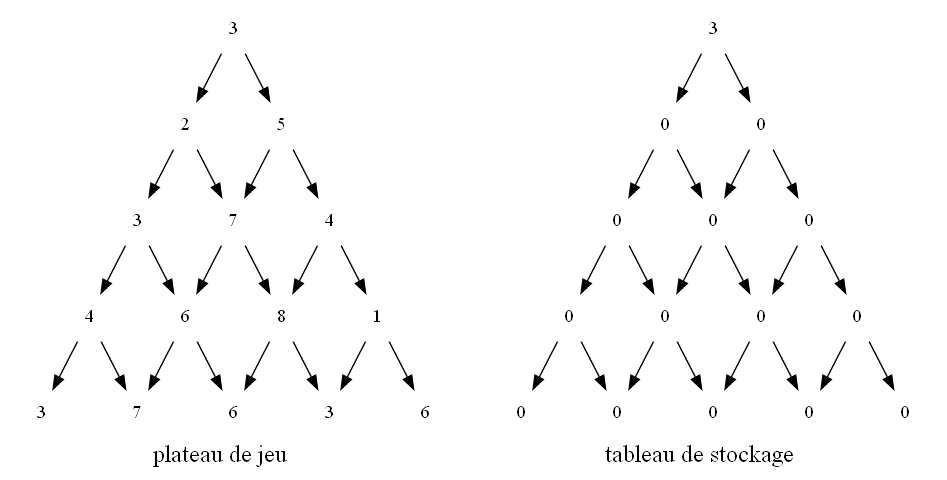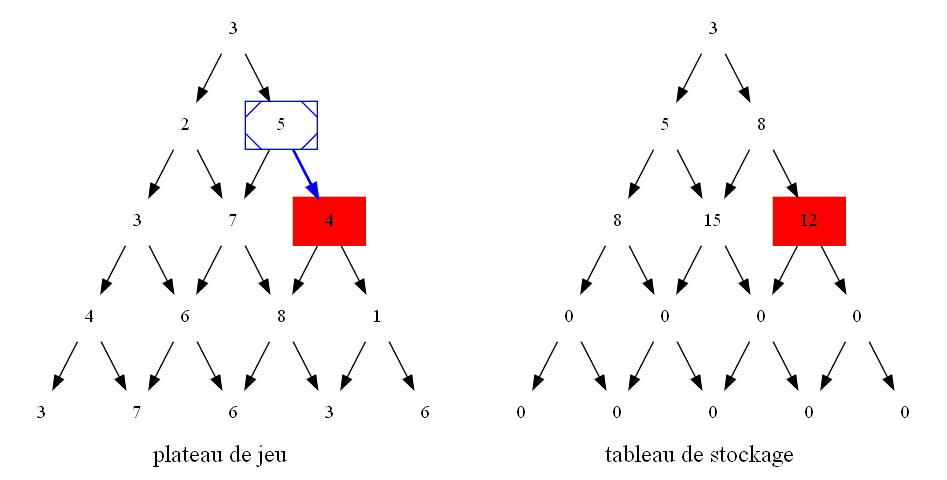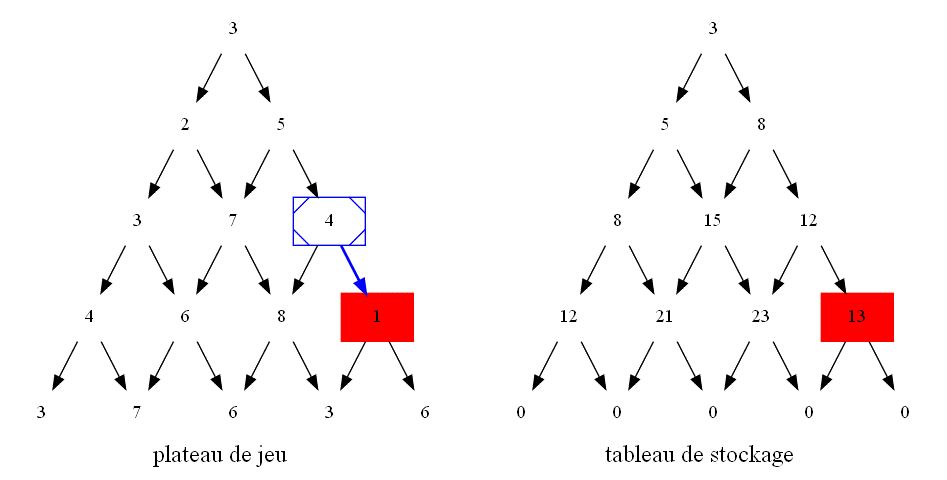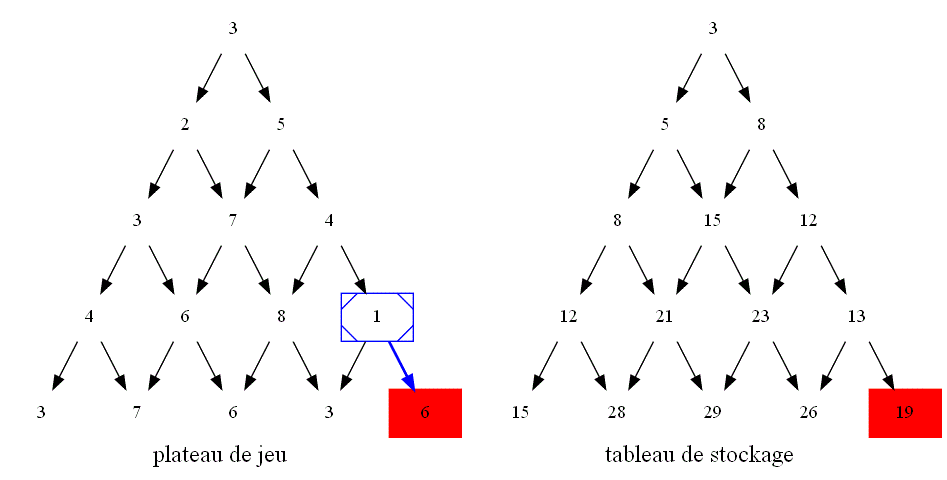
Cet algortihme est encore améliorable :

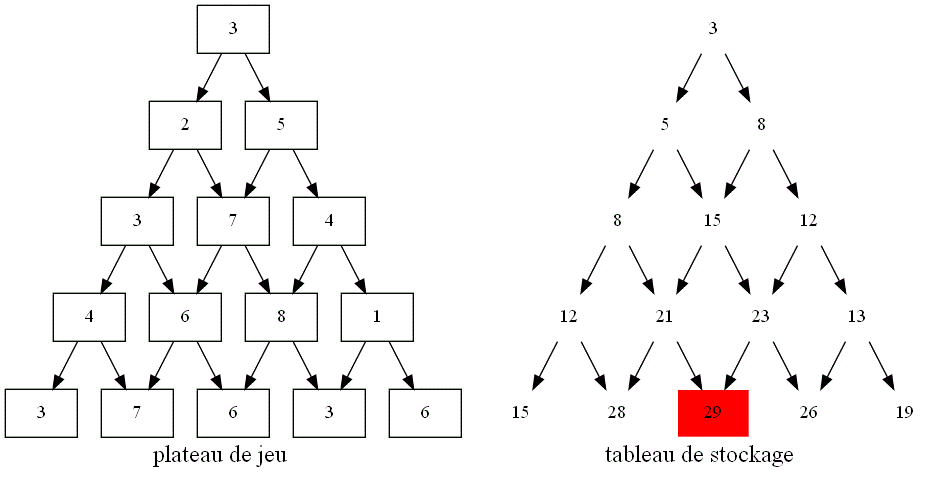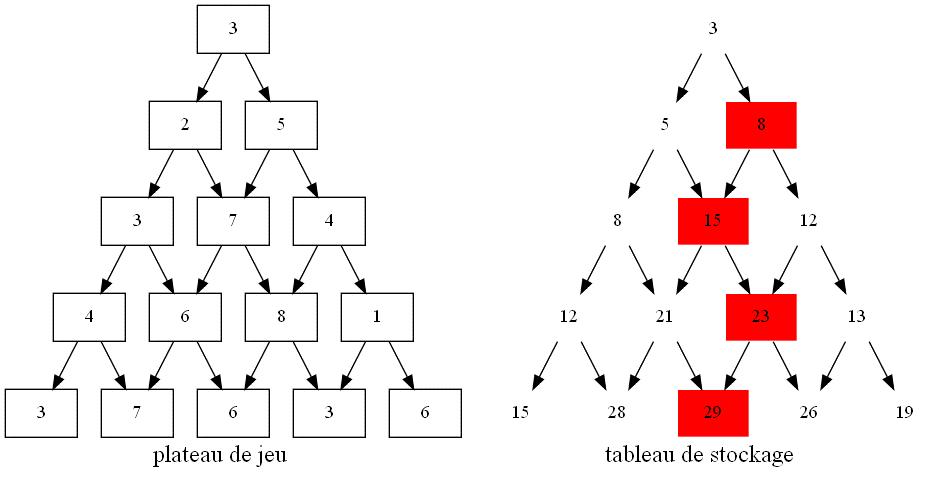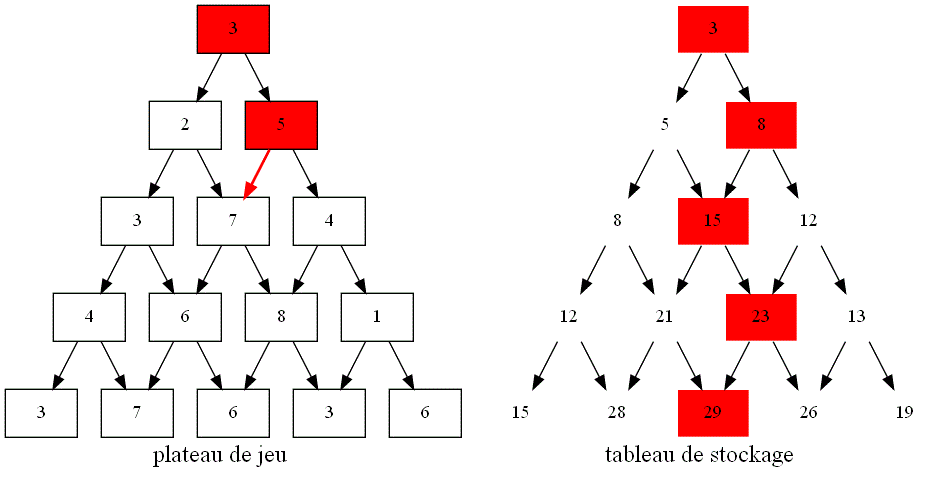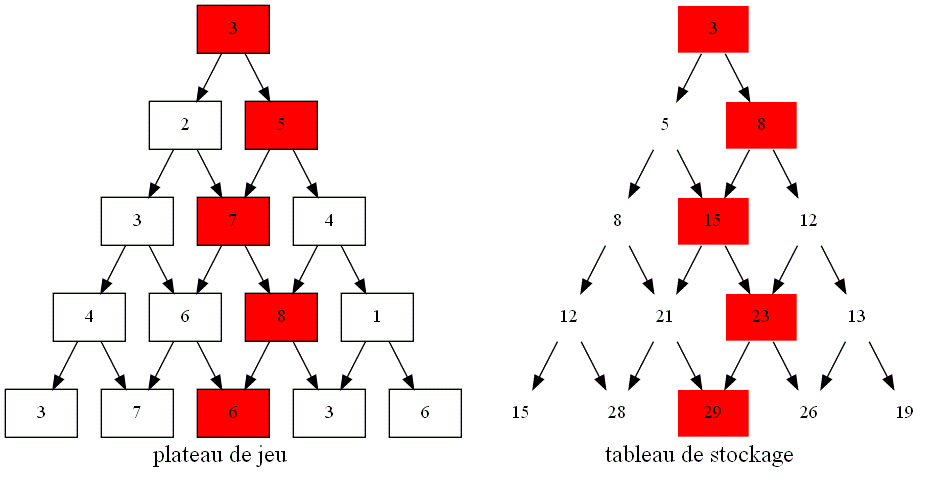
Problème du rendu de monnaie

Rappel du problème : On cherche à rendre la monnaie avec un nombre minimal de pièces sachant que l'on dispose d'un nombre illimité de pièces dans un système monétaire donné.

Version gloutonne

Nous avons vu l'année dernière que l'on peut résoudre ce problème avec un algorithme glouton.

On peut résumer la stratégie gloutonne ainsi :

On prend la pièce de plus haute valeur possible (mais inférieure à la somme restant à rendre)
On poursuit cette démarche jusqu'au moment où la somme à rendre devient nulle (ou qu'on ne peut plus réduire le somme à rendre)

Voici une écriture possible de cet algorithme glouton :

def glouton(pieces:list, somme:int) -> list:
    """
    pieces est une liste dont les éléments sont les valeurs faciales des pièces rangées par ordre décroissant
    somme est la somme à rendre
    Cette fonction renvoie la liste des pièces à rendre (ou None en cas d'échec de la méthode gloutonne)
    """
    i = 0                               # index de la pièce qu'on va regarder
    rendu = []                          # liste des pièces rendues
    while somme>0:                      # tant qu'il reste une somme à rendre
        if pieces[i] > somme:           # si la pièce considérée est trop grande
            i = i+1                     # passage à la valeur faciale inférieure : la suivante
        else:                           # plus gande valeur de pièce possible que l'on peut rendre
            rendu.append(pieces[i])     # cette pièce est à rendre
            somme = somme - pieces[i]   # la somme restant à rendre est réduite
    if somme == 0:                        # cas où la méthode permet de tout rendre
        return rendu                    # solution renvoyée
    else:                               # cas où la méthode de convient pas
        return None                     # pas de renvoi fallacieux alors

1. Vérifier qu'avec le système euros pieces = [500, 200, 100, 50, 20, 10, 5, 2, 1,0.50, 0.20, 0.10, 0.05, 0.02, 0.01] la fonction précédent renvoie une solution quelle que soit la somme à rendre somme choisie.
2. Trouvez-vous une solution plus optimale que celle renvoyée par la fonction, c'est-à-dire pouvez-vous trouver une solution premettant d'obtenir la somme à rendre avec moins de pièces en tout ?
Avant la décimalisation définitive de 1971, le système monétaire britannique reposé sur une subdivision de valeurs qui remontait à l'époque carolingienne.

Voici les principales valeurs de cet ancien système :
- 1 penny
- 3 pence (pluriel de penny)
- 6 pence (ou demi-shilling)
- 12 pence (appelé shilling)
- 24 pence (appelé florin)
- 30 pence (appelé demi-couronne)
- 60 pence (appelé couronne)
- 240 pence (appelé livre)
(source : wikipedia)
1. Que renvoie la fonction pour rendre 48 pence avec le système imperial où pieces = [240,60,30,24,12,6,3,1] ?
2. Trouvez-vous une solution plus optimale que celle renvoyée par la fonction, c'est-à-dire pouvez-vous trouver une solution permettant d'obtenir la somme à rendre avec moins de pièces en tout ?
1. Que renvoie la fonction pour rendre 11 pence avec le système suivant où pieces = [20, 10, 5, 2] ?
2. Trouvez-vous une solution plus optimale que celle renvoyée par la fonction, c'est-à-dire pouvez-vous trouver une solution permettant d'obtenir la somme à rendre avec moins de pièces en tout ?
Que pensez-vous de cet algorithme ?

Programmation dynamique

Étape 1 : mise en place d'une solution récursive

On veut un algorithme récursif qui renvoie le nombre minimal de pièces pour un système monétaire donné suffisant pour rendre une somme donnée, lorsqu'une telle solution existe.
Plus tard, nous chercherons à améliorer cet algorithme, en particulier pour obtenir la liste des pièces de cet optimum.

On note $somme$ la somme à rendre.
Le cas d'arrêt correspond au cas le plus simple de $somme$.
Pour le cas général, l'idée repose sur le fait que pour une pièce de valeur $p_i$ du sytème monétaire, si $p_i$ est utilisée lors d'une solution optimale alors pour rendre la somme $somme$ de manière optimale, il suffit de rendre $somme-p_i$ de manière optimale.
Il suffit donc de choisir parmi tous les choix possibles de $p_i$ celui qui permet de minimiser le nombre de pièces pour rendre la somme.

Par exemple :
On considère le système monétaire [1, 2, 5, 10].
On suppose que la somme à rendre est de 6 euros (somme = 6) : on cherche le nombre de pièces miniales à rendre.
On a étudié les 4 cas suivants :

On utilise une pièce de 1 euro (pi = 1) : il suffit de connaître le nombre minimal à rendre alors pour les 5 euros restant. Ce dernier nombre est 1 (une seule pièce de 5€ suffit) si bien que 2 pièces suffisent alors pour rendre ces 6 euros.
On utilise une pièce de 2 euros (pi = 2) : il suffit de connaître le nombre minimal à rendre alors pour les 4 euros restant. Ce dernier nombre est 2 (deux pièces de 2€ au mieux) si bien que 3 pièces suffisent alors pour rendre ces 6 euros.
On utilise une pièce de 5 euros (pi = 5) : il suffit de connaître le nombre minimal à rendre alors pour le dernier 1 euro restant. Ce dernier nombre est 1 (une seule pièce de 1€ suffit) si bien que 2 pièces suffisent alors pour rendre ces 6 euros.
On ne peut pas utiliser le billet de 10 euros (pi = 10) qui dépasse la somme à rendre.

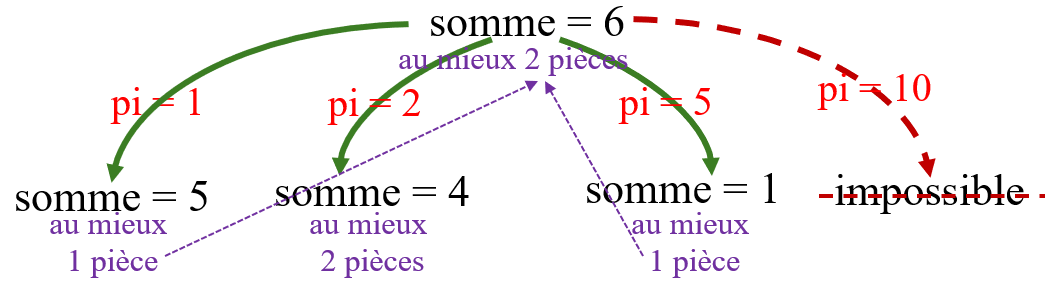
Ainsi au mieux, il suffit d'utiliser 2 pièces pour rendre 6 euros.

Compléter le programme récursif suivant afin que la fonction récursursive renvoie soit le nombre minimal de pièces nécessaires, soit inf si une telle solution n'existe pas.

Dans cet algorithme, inf symbolisera une impossibilité puisque l'on cherche ici un minimum.

inf est un objet du module math modélisant la notion mathématique de $+\infty$ : tout nombre entier (ou flottant) sera forcément strictement inférieur à cet objet.

from math import inf        # objet modélisation la notion de +infini
def rendu_rec(pieces: list, somme: int) -> int:
    """
    pieces est une liste dont les éléments sont les valeurs faciales des pièces
    somme est la somme à rendre
    Cette fonction récursive renvoie le nombre minimal de pièces à rendre.
    Si aucune solution n'existe, cette fonction renvoie inf
    """
    if somme == ...:
        return ...
    else:
        mini = inf
        for pi in pieces:
            ...  # une ou plusieurs lignes
        return mini

Tester la fonction récursive avec comme système monétaire [1,3,6,12,24,30,60,240] et comme somme $10$ puis $48$. Que remarquez-vous pour $48$ ?

Voici ci-dessous le graphe des résultats obtenus par le programme récursif précédent pour une somme valant $11$ et comme système monétaire [1, 3, 6, 12, 24, 30, 60, 240] ; chaque nombre présent dans un sommet correspond à la somme à rendre encore tandis que chaque arc lie une somme à une autre réduite de la valeur d'une pièce du système :

Voici un arbre représentant les différents résultats obtenus par ce même programme avec les mêmes entrées :

Comme l'exécution de chacune des étapes est longue, voici une image de l'arbre complet obtenu :

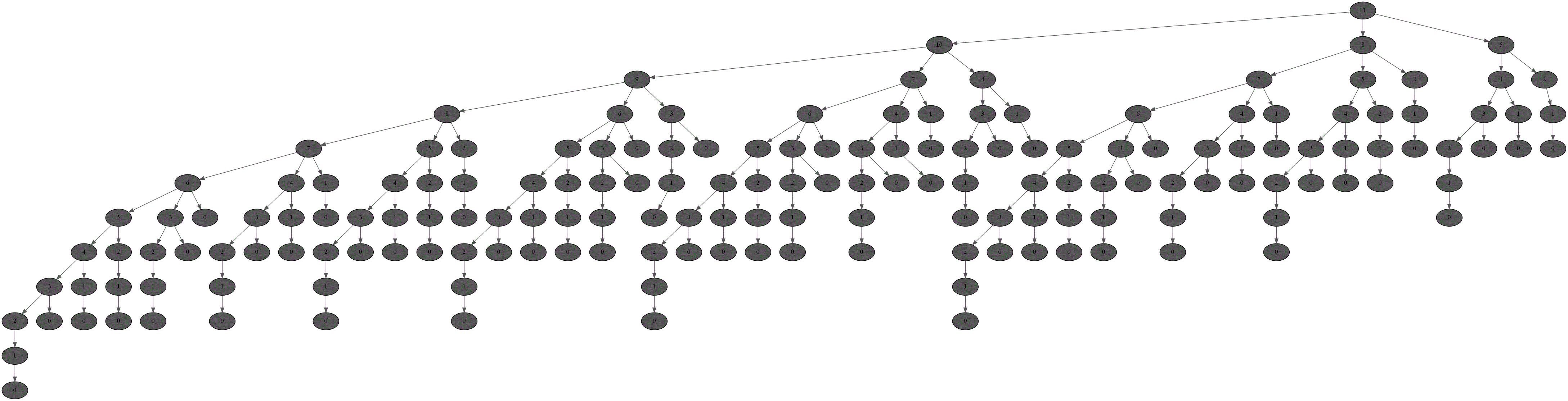
Pourquoi la fonction récursive est si longue à renvoyer le résultat attendu, même pour un petit nombre comme 48 ?
Comment faire pour obtenir un algorithme plus rapide donnant bien le nombre minimum de pièces à rendre ?
En regardant le gif précédent, déteminer quel est le nombre entier renvoyé par la fonction récursive dans le cas où la somme valant $11$ et le système monétaire [1, 3, 6, 12, 24, 30, 60, 240].

Étape 2 : mémorisation et passage à une version itérative

Dans le gif précédent, on a vu que le coût en temps de la fonction récursive est très important du fait de la redondance des mêmes calculs et qu'il suffirait d'utiliser un tableau pour mémoriser les résultats des couleurs déjà faits.

On suppose ici comme sytème monétaire simplement [1, 3, 6].
Recopier et compléter à la main le tableau suivant qui à chaque $somme$ associe le nombre minimal de pièces du système monétaire à rendre.

somme	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
nombre minimal	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...

Proposer un algorithme itératif qui répond au problème du rendu optimal en renvoyant le nombre minimal de pièces à rendre dans un système monétaire donné.

Utiliser un tableau (liste en Python) memoire de taille somme+1 qui va mémoriser progressivement le nombre minimal de pièces à rendre pour toutes les valeurs inférieures ou égales à somme.
Initialiser cette liste judicieusement en s'inspirant de l'exercice précédent fait à la main.
Pour calculer la valeur de memoire aidez-vous de l'algorithme récursif déjà obtenu pour voir comment calculer memoire[i] en fonction des valeurs précédentes memoire[j] où $j\lt i$.

Déterminer la compléxité de l'algorithme itératif précédent.

Obtention de la liste optimale des pièces à rendre

On admet que le nombre minimal de pièces à rendre pour le système monétaire [1, 3, 6] est donné pour les première valeurs par le tableau suivant :

somme	0	1	2	3	4	5	6	7	8	9	10	11	12	13
nombre minimal	0	1	2	1	2	3	1	2	3	2	3	4	2	3

Sans chercher à deviner directement quel est l'ensemble des pièces à rendre, utilisez le tableau précédent et la relation memoire[i] = min(memoire[i], 1+memoire[i-pi]) (comparaison entre le minimum connu pour i et le nombre de pièces nécessaires si la pièce de valeur pi est utilsiée) pour déterminer l'ensemble minimal des pièces à rendre pour donner 13.

Adapter l'algorithme itératif déjà obtenu afin d'obtenir pour un système monétaire choisi et une somme donnée à rendre l'ensemble minimal de pièces à rendre.

Comme suggéré dans l'exercice précédent, il peut être intéressant d'utiliser une deuxième liste qui stockera soit la valeur précédente à considérer une fois une pièce pertinente rendue (préférable en coût mémoire), soit une liste minimale des pièces à rendre pour les valeurs précédentes.

Exercices

Cet exercice est issu d'un exercice proposé par Basile Sauvage lors de la formation en DIU à l'Université de Reims.

Un magasin vend des pralines par paquets de 6, 9 ou 20.
Un nombre entier $n$ sera appelé dans cet exercice nombre à pralines si, et seulement si, ce nombre $n$ peut s'écrire comme une somme de 6, de 9 et de 20.
Pour simplifier la suite, on supposera que 0 est un nombre à pralines (en achetant aucun paquet de pralines, on peut obtenir ce nombre)
Par exemple, $21=6+6+9$ donc $21$ est un nombre à pralines, par contre 11 n'est pas un nombre à pralines.
Posons $Pral(n)$ un booléen qui faut true si, et seulement si, $n$ est un nombre à pralines.

1. Que vaut $Pral(n)$ lorsque $n$ est négatif ? Lorsque $n=0$ ?
2. Proposer une formule de récurrence sur $Pral(n)$.
  
  hormis les deux cas précédents directs, utiliser les opérateurs or ou and sur les booléens pour exprimer $Pral(n)$ en fonction de valeurs précéentes.
3. En déduire une fonction récursive est_pral_rec qui prend en paramètre un nombre entier et renvoie un booléen correspondant à $Pral(n)$.
Dessinez un graphe simplifié des dépendances sur un tableau donnant les premières valeurs de $n$.
En déduire une fonction itérative est_pral qui prend en paramètre un nombre entier positif et renvoie un booléen correspondant à $Pral(n)$.
Quel est la complexité de cette fonction ? (constante, linéaire, quadratique, exponentielle, ...)
En déduire un algorithme qui reconstruit une solution (nombre d'occurences de 6, de 9 et de 20) dans le cas où $Pral(n)=$True.

La distance d'édition (ou distance de Levenstein ou distance d'Ulam) est un algorithme permettant de comparer deux chaînes de caractères $A$ et $B$ définies sur un alphabet fini $L$. Cette distance est définie comme le nombre d'opérations minimum qui permet de passer de la première chaîne à la seconde en ne considérant que trois seules opérations possibles pour passer d'une chaîne à l'autre :

Disparition d'une lettre $a$ de la chaîne $A$,
Insertion d'une lettre $b$ parasite,
Remplacement d'une lettre $a$ de la chaîne $A$ par une lettre $b$.

Pour simplifier, on suppose ici que toutes ces modifications ont un coût de 1.

Notation utilisée dans cet exercice :

On considère une chaîne $A$ de longueur $n$ et une chaîne $B$ de longueur $m$.
Les $n$ éléments de $A$ seront indexés de 0 à $n-1$.
on note $d(i,j)$ la distance minimale entre les premières lettres de $A$ indexées de 0 à $i$ et les premières lettres de $B$ indexées de 0 à $j$.
Par convention, $i=-1$ ou $j=-1$ signifie que l'on considère une chaîne vide avec : $d(-1,-1)=0$, $d(-1,j)=j+1$ et $d(i,-1)=i+1$.

Le but est d'établir une relation de récurrence sur $d$ liant $d(i,j)$ avec des valeurs précédentes $d(k,l)$, où $k\le i$ et $l\le j$.
Pour cela, on étudie les cas suivants :
1. Quel cas entre la disparition, l'insertion ou le remplacement d'une lettre à préciser correspond au cas où $d(i,j)=d(i-1,j)+1$ ?
2. On suppose que la lettre $B[j]$ est ajoutée. Déterminer une expression de $d(i,j)$ en fonction d'une valeur précédente.
3. On suppose que les lettres $A[i]$ et $B[j]$ sont identiques. Déterminer une expression de $d(i,j)$ en fonction d'une valeur précédente.
4. On suppose qu'il y a eu un remplacement : les lettres $A[i]$ et $B[j]$ sont différentes.
  Déterminer une expression de $d(i,j)$ en fonction d'une valeur précédente.
5. Justifier que dans le cas général, pour $i\ge 0$ et $j\ge 0$, $d(i,j)=min(d(i-1,j)+1,d(i,j-1)+1,d(i-1,j-1)+(0\ si\ A[i]=B[j]\ 1\ sinon))$.
Proposer une fonction dist_edit_rec qui prend en paramètre deux chaînes de caractères et qui renvoie la distance de Levenstein entre ces deux mots en s'aidant de la relation de récurrence trouvée sur $d(i,j)$.
- (1 if a != b else 0) permet d'obtenir 1 si les variables a et b sont différentes et 0 sinon.
- ch[:-1] permet d'obtenir la sous-chaîne formée de tous les caractères de ch hormis le dernier.
1. Dresser un tableau de taille $n\times m$ qui stocke les couples $(i,j)$ avec $-1\le i \le n$ et $-1\le j \le m$.
  Attention ! Ici, on considère la possibilité -1 pour considérer le cas où une des chaînes des caractères est vide.
2. En déduire un graphe de dépendance lié à la fonction récursive dist_edit_rec
3. Lorsque l'on considère une case sur la première ligne (hormis la première case), quelle(s) flèche(s) y peu(ven)t y aboutir ?
4. Lorsque l'on considère une case sur la première colonne (hormis la première case), quelle(s) flèche(s) y peu(ven)t y aboutir ?
5. Lorsque l'on considère une case en dehors de la première colonne et de la première ligne, quelle(s) flèche(s) y peu(ven)t y aboutir ?
6. Quelle structure de données permet de facilement stocker la distance de Levenstein associée à chaque couple $(i,j)$ ?
Proposer une fonction itérative dist_edit qui prend en paramètre deux chaînes de caractères et qui renvoie la distance de Levenstein entre ces deux mots en s'adiant de la relation de récurrence trouvée sur $d(i,j)$.
- Pour la mémorisation des valeurs déjà calculées, utiliser un dictionnaire qui associe à chaque couple $(i,j)$ sa distance $d(i,j)$.
- Pour gérer le minimum, il peut être utilise de considérer une liste temporaire dans laquelle on stocke les distances liées à chaque flèche.
- La fonction enumerate prend en paramètre une chaîne de caractères et renvoie un itérable index,caractere qui permet d'obtenir le caractère et son index dans la chaîne. exemple :
```
for index,caractere in enumerate('mot'):
    print(index,caractere)
```
  renvoie :
```
0 m
1 o
2 t                                            
```
Quelle est la complexité en temps de cette fonction ?
Proposer une fonction dist_edit_chem qui prend en paramètre deux chaînes de caractères, qui renvoie la liste des couples $(i,j)$ correspondant au trajet dans le tableau permettant de modifier la première chaîne en la seconde en un coût minimal.
De plus, cette fonction affiche la succession des insertions, suppressions et remplacements avec leur position permettant de passer de la première chaîne en la seconde.
Exemple :
```
distance_edition_chemin("essai","hesta")
```
affiche :
```
L'élement h a été inséré en position 0 dans la chaîne initiale.
L'élement s a été remplacé en position 3 par t.
L'élement i a été supprimé en position 4 dans la chaîne initiale.
```
et renvoie :
```
[(-1, -1), (-1, 0), (0, 1), (1, 2), (2, 3), (3, 4), (4, 4)]
```
Une portion de gène est passé de la séquence $ATTACAGTA$ à celle $ACTATACGTT$.
Déterminer les modifications permettant de passer d'une séquence à l'autre "au moindre coût", c'est-à-dire avec le moins de délétion, de modification ou d'insertion d'un nucléotide $A$, $C$, $G$ ou $T$.

Cette distance est très utile dans différents domaines :

la réalisation de correcteurs orthographiques,
la reconnaissance optique de caractères,
l'étude de la proximité de langues,
repérer les mutations probablement subies par une séquence ADN,
similarité des arbres phylogénétiques, ...

Exercice du Baccalauréat

Savoirs et savoir-faire

que l'utilisation d'un tableau pour mémoriser des valeurs déjà calculées peut permettre de réduire le temps d'exécution d'un algorithme,
la notion de programmation dynamique.

introduire un tableau de mémorisation dans un algorithme afin d'éviter les calculs redondants,
Dresser un graphe de dépendance à partir des appels récursifs,
réécrire un algorithme récursif en un algorithme itératif.

Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲