Demandez le programme !

La notion de récursivité
Exemple introductif
Certains problèmes peuvent sembler difficile à résoudre d'emblée. Vous allez découvrir une manière d'écrire des algorithmes qui permet de résoudre élégamment certains problèmes. Voilà un outil puissant !
Imaginez que vous ayez à créer une fonction puissance qui prend deux arguments $x$, un réel, et $n$, un entier naturel, et qui renvoie $x^n$.
Une méthode directe est de partir de 1 puis d'écrire une boucle répétitive qui permet d'aboutir par multiplications successives à $x^n$ en utilisant le fait que $x^n=x \times x^{n-1}$. Voici une possibilité :
def puissance(x: float, n: int) -> float:
p = 1
for i in range(n):
p = x*p
return p
Tester le code précédent pour vérifier que la fonction puissance renvoie bien $x^n$.
Si besoin, vous pouvez utiliser le site Trinket.
Mais si on faisait l'inverse ? On part de ce qui est compliqué $x^n$ et on voit comment simplifier progressivement pour arriver à 1 !
Cela est possible, toujours en utilisant le fait que : $\begin{equation} x^n=\begin{cases} 1, & \text{si $n=0$}.\\ x \times x^{n-1}, & \text{sinon}. \end{cases} \end{equation}$
Ainsi, on aurait l'idée d'écrire un programme comme celui ci-dessous :
def puissance_rec(x: float, n: int) -> float:
if n == 0:
return 1
else:
return x * puissance_rec(x, n-1)
-
Réalisez une trace d'exécution de l'algorithme précédent avec $x=2$ et $n=3$. Est-ce que
puissance_rec(2,3)renvoie bien $2^3$ ? -
Recopiez le script précédent puis testez-le plusieurs fois, par exemple avec $x=2$ et $n=10$, s'interrogez si
puissance_rec(2,10)renvoie bien $2^{10}$.
Aussi étonnant que cela puisse paraître de prime abord, cela fonctionne !
Nous avons ainsi créé une fonction
puissance_rec qui s'appelle elle-même : on appelle cela de la récursivité.
Notion de récursivité
On qualifie de récursive toute fonction qui s'appelle elle-même.
Outre l'exemple du 1.1 (cf. lien direct), voici un deuxième exemple.
Dans une grande
boite de Pétri contenant un milieu nutritif riche sont déposées 10 bactéries.
On suppose que chaque heure le nombre
de bactéries est multiplié par 4.
Voici une fonction récursive nb_bact qui renvoie le nombre de
bactéries au bout de $n$ jours, $n$ étant un entier naturel saisi comme argument.
def nb_bact(n: int) -> int:
if n == 0:
return 10
else:
return 4 * nb_bact(n-1) Cette fonction permet d'évaluer le nombre de bactéries au bout d'une journée (en supposant le milieu nutritif suffisant) :
>>> nb_bact(24)
2814749767106560
Pour ceux qui ont suivi la spécialité mathématique en première, vous pouvez y retrouver une suite :
le nombre de bactéries au bout de $n$ heures est donné par $u_n$.
Cette suite $(u_n)$ est définie
par la relation de récurrence
suivante : \begin{equation} u_n=\begin{cases} 10 &, \text{si $n=0$}.\\ 4 \times u_{n-1} &, \text{si $n>0$}. \end{cases} \end{equation}
Le nombre de bactéries obtenu au bout de 24 heures s'écrit dans le langage des suites comme égale à $u_{24}$.
Repérer parmi les fonctions suivantes celles qui sont récursives :
fonction f1 :
def f1(n: int) -> int:
if n == 0:
return 0
else:
return n-1
fonction f2 :
def f2(n: int) -> int:
if n == 0:
return 0
else:
return f2(n-1)
fonction f3 :
def f3(n: int) -> int:
if n == 0:
return f3(n-1)
else:
return 0
fonction f4 :
def f4(n: int) -> int:
if n == 0:
return n-1
else:
return 0
fonction f5 :
def reduire(n:int) -> int:
return n-1
def f5(n: int) -> int:
if n == 0:
return 0
else:
return reduire(n)
Voici une fonction mystère nommée myst :
def myst(l: list) -> int:
if l == []:
return 0
else:
l.pop(0) # suppression du premier terme de la liste l
return 1 + myst(l) -
Pourquoi cette fonction
mystest une fonction récursive ? -
Testez cette fonction avec quelques listes.
-
Quel est le rôle de cette fonction
myst?
Condition d'arrêt
-
Copiez et lancez le script suivant :
def appel() -> None: print("Allô ?") return appel() -
Que remarquez-vous ? Comment expliquez-vous cela ?
Dans l'exercice traité ci-dessus, les appels s'enchaînent sans rien pour mettre un terme à cet enchaînement : le système interrompt le programme en générant une erreur quand ses capacités sont dépassées. Nous verrons dans la prochaine partie ce qu'il se passe au niveau mémoire lors d'appels récursifs : vous comprendrez mieux alors pourquoi physiquement il y a un problème occasionné. Ainsi :
Dans toute fonction récursive, il est nécessaire d'avoir une condition d'arrêt ; on parle aussi de condition de terminaison.
Voici une réécriture de la fonction de l'exercice précédent où une condition d'arrêt a été rajoutée ainsi qu'une variable sur laquelle porte cette condition d'arrêt :
def appel(n: int) -> None:
if n == 0: # n=0 est ici la condition d'arrêt
print("Allô ?") # arrêt des appels
else:
print("Allô ?")
return appel(n-1)
Ainsi, l'exécution de appel(3) conduit à l'affichage suivant :
>>> appel(3)
Allô ?
Allô ?
Allô ?
Allô ?
Attention ! L’existence d’une condition d’arrêt ne signifie pas que l’appel récursif s’arrête grâce à celle-ci.
Prenons l’exemple de l’exécution de appel(-1) :
-
appel(-1)conduit par appel récursif à l'exécution deappel(-2), -
appel(-2)conduit par appel récursif à l'exécution deappel(-3), -
appel(-3)conduit par appel récursif à l'exécution deappel(-4), -
...
La condition d’arrêt $n=0$ n’est jamais atteinte et on obtient une suite infinie d’appels.
Ainsi, il est important d'ajouter une précondition pour imposer que $n$ soit un entier naturel. D'où :
def appel(n: int) -> None:
assert type(n)==int and n >=0, "Vous devez saisir un entier naturel"
if n == 0: # n=0 est ici la condition d'arrêt
print("Allô ?") # arrêt des appels
else:
print("Allô ?")
return appel(n-1)
Revoici la fonction puissance_rec vue à la fin du 1.1 (cf. lien direct) :
def puissance_rec(x: float, n: int) -> float:
if n == 0:
return 1
else:
return x * puissance_rec(x, n-1) -
La condition d'arrêt est : $n=0$.
-
Cette condition correspond aussi au cas "simple" où $x^0=1$ : on connaît le résultat à faire renvoyer par la fonction : 1.
-
Une fonction récursive est une fonction qui s'appelle elle-même.
-
Une fonction récursive nécessite l'existence d'une condition d'arrêt où la fonction ne s'appelle pas elle-même.
-
Dans une fonction récursive, il faut s’assurer que la condition d’arrêt soit atteinte après un nombre fini d’appels.
Cette condition d'arrêt ne peut en aucun cas être un appel récursif. -
Souvent, il est pertinent de choisir une condition d'arrêt correspondant à un "cas simple" pour lequel vous connaissez la valeur à renvoyer.
On veut réaliser un château de cartes géants qui prolonge la château de l'image ci-dessous :

On note $n$ le nombre d'étages du château et $nb\_cartes(n)$ le nombre de cartes nécessaires pour réaliser un château à $n$ étages.
On admet que l'on peut connaître le nombre $nb\_cartes(n+1)$ de cartes nécessaires pour un château à $n+1$ étages si on connaît déjà le nombre $nb\_cartes(n)$ en utilisant la relation suivante (appelée relation de récurrence en mathématiques) : $$nb\_cartes(n+1)= nb\_cartes(n)+2+3 \times n$$
On veut à partir de ces informations construire une fonction récursive nommée nb_cartes qui renvoie finalement le nombre $nb\_cartes(n)$ si en argument lui est entré le nombre $n$ d'étages voulus au château.
Voici
un script incomplet pour cette fonction :
def nb_cartes(n: int) -> int:
if ...........: # condition d'arrêt
return .............
else: # cas général
return .............
-
En vous aidant de la relation de récurrence liant $nb\_cartes(n+1)$ et $nb\_cartes(n)$, complétez le retour du cas général.
-
Déterminez quel cas simple correspond à la condition d'arrêt puis complétez son renvoi.
-
Testez votre fonction obtenue.
Vous pouvez utiliser l'image ci-dessus pour connaître quelques valeurs à obtenir.
-
Rajouter une précondition pour assurer le bon fonctionnement de l'algorithme.
Voici un exercice à faire en autonomie pour tester votre maîtrise de
la récursivité en lien avec la notion de suite en mathématiques.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Si en spécialité mathématiques vous n'êtes pas à l'aise sur l'utilisation
de Python pour obtenir un terme particulier d'une suite, traitez aussi
la version itérative.
Dans l'exercice précédent, on est certain que la récursion prend fin car chaque nouvel appel se fait avec un paramètre $n$ qui diminue.
Pour s'assurer de la terminaison d'un algorithme récursif, il suffit d'identifier une suite strictement décroissante d'entiers positifs ou nuls.
On retrouve cette idée de variant de boucles qui permet de
s'assurer qu'une boucle while se termine à coup sûr.
Revoici la fonction puissance_rec vue à la fin du 1.1 (cf. lien direct) :
def puissance_rec(x: float, n: int) -> float:
if n == 0:
return 1
else:
return x * puissance_rec(x, n-1)
La condition d'arrêt ne suffit pas : on ne peut pas réécrire la fonction puissance_rec comme ci-dessous :
def puissance_rec_fausse(x: float, n: int) -> float:
if n == 0:
return 1
else:
return puissance_rec_fausse(x, n+1)/x
-
La condition d'arrêt est : $n=0$ est bien présente.
-
Cependant à chaque appel le second argument $n$ augmente de 1.
La factorielle d'un entier naturel $n$ non nul, notée $n!$, est le produit de tous les nombres entiers compris entre 1 et $n$, c'est-à-dire : $n!=1 \times 2 \times ... \times (n-1) \times n$.
- $1!=1$.
- $4!=1 \times 2 \times 3 \times 4 = 24$,
- $6!=1 \times 2 \times 3 \times 4 \times 5 \times 6 = 720$,
Il existe une relation "simple" entre $n!$ et $(n-1)!$.
En effet : $n!=1 \times 2 \times ... \times (n-1) \times n = \underbrace{1 \times 2 \times ... \times (n-1)}_{(n-1)!} \times n = (n-1)! \times n$,
-
Écrivez une fonction récursive
factqui prend comme argument l'entier non nul $n$ et qui renvoie $n!$ : -
Quelle est la condition d'arrêt de votre fonction récursive ?
-
Pourquoi pouvez-vous être certain.e.s que la situation de terminaison sera atteinte après un nombre fini d'appels récursifs ?
-
Rajouter une précondition.
Voici un exercice à faire en autonomie pour tester votre maîtrise de
la récursivité.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice.
Vous pouvez si besoin basculer vers la version à trous pour la "Question 1 : somme des chiffres", c'est ce qui est attendu ici.
Commencer par réfléchir à la condition d'arrêt : Dans quels cas il est très simple
de connaître la somme des chiffres d'un nombre ?
Ensuite, lire la partie "Rappels sur la division euclidienne" et comprendre
que pour calculer la somme des chiffres de 409, il suffit de remarquer qu'il suffit calculer
9 + la somme des chiffres de 40.
Dans le cas général attendu dans le else, il suffit de traduire la remarque ci-dessus dans le cas général
en se servant des opérateurs de la division euclidienne.
Le but est d'écrire une fonction récursive somme qui prend en argument une liste de nombres et qui renvoie la somme de ce nombres.
-
Quel cas simple peut correspondre à une condition d'arrêt pour cette fonction ?
-
Pour le cas général, proposez un appel récursif à la fonction
sommeoù la liste est diminuée d'un élément.Vous pouvez vous aider :-
soit d'une partie du script de l'exercice 4 (cf. lien direct),
-
soit en utilisant le slicing :
liste[1:]correspond à la liste initiale où le premier élément a été ôté.Sachez que le slicing est hors programme donc non exigible en évaluation mais il permet ici d'écrire facilement le code voulu sans utiliser la méthode
pop.
-
-
Testez votre fonction
somme.Vous devez par exemple obtenir comme exécution de
somme([1, 2, 3])le nombre 6. -
Quelle suite de nombres entiers strictement décroissante peut être exhibée ici afin de justifier la terminaison de l'algorithme écrit ?
On veut obtenir une fonction inverser qui inverse une chaîne de caractères ; par exemple, inverser("aBc45f!") renvoie "!f54cBa". Pour cela, la fonction extrait le premier élément puis fait un
appel récursif (à elle-même) pour ajouter à la fin cet élément extrait.
Voici une partie du script de cette fonction inverser :
ch[1:] correspond à la chaîne de caractère ch auquel le premier élément, celui ch[0], a été ôté. Par exemple, si
ch="aBc45f!", alors ch[1:] correspond
à "Bc45F!"
def inverser(ch: str) -> str:
n = len(ch)
return inverser(ch[1:]) + ch[0] # on ajoute le premier terme au résultat de l'inversion du reste de la chaîne -
Le script précédent est-il fonctionnel ? Pourquoi ?
Si vous n'arrivez pas à répondre à la question, exécutez le code précédent et s'il ne fonctionne pas lisez l'éventuel message d'erreur renvoyé par l'interpréteur.
-
Rajoutez une condition d'arrêt à ce script pour le rendre fonctionnel.
Pensez au cas le plus simple d'une chaîne de caractères à inverser.
-
Testez votre script augmenté d'une condition d'arrêt.
Exemple d'exécution à obtenir:
>>>inverser("aBc45f!") "!f54cBa"
On appelle palindrome un mot (ou une phrase) qui se lit de la même façon à de gauche à droite comme de droite à gauche, si on ne tient pas compte des espaces.
Exemples :
-
"KAYAK" est un palindrome,
-
La phrase "ESOPE RESTE ICI ET SE REPOSE" est aussi un palindrome, puisqu'en ôtant les espaces, la chaîne devient "ESOPERESTEICIETSEREPOSE".
-
Par contre, "AIMA" n'est pas un palindrome car "AIMA" est différent de "AMIA".
Voici une partie d'une fonction est_palindrome qui prend comme argument une chaîne de caractères (sans espace) et qui renvoie un booléen : True si le mot saisi comme argument est un palindrome, False sinon.
def est_palindrome(ch: str) -> bool:
bool = True
n = len(ch)
if ch[0] == ch[n-1]: # caractères extrêmes de la chaîne égaux
ch2 = ch[1:n-1] # chaîne de caractères extraites de ch où le premier caractère (ch[0]) et le dernier (ch[n-1]) ne sont plus pris.
return est_palindrome(ch2)
else:
bool = False
return bool
Rajouter une condition d'arrêt à cette fonction et modifier le code précédent afin de rendre fonctionnelle la fonction est_palindrome.
Voici un exercice à faire en autonomie pour tester votre maîtrise de
la récursivité tout en révisant l'algorithme glouton de rendu de monnaie
vu en fin d'année dernière.
Cet exercice est issu du site collaboratif de la forge.
Commencer par traiter le cas où la méthode append est
à utiliser en cliquant sur ce lien pour accéder à l'exercice.
Basculer dans l'éditeur vers la version à trous avec append si besoin.
Finir par traiter le cas où la concaténation de listes est
à utiliser en cliquant sur ce lien pour accéder à l'exercice.
Basculer dans l'éditeur vers la version à trous avec concaténation si besoin.
Identifier une suite strictement décroissante d'entiers positifs ou nuls permet de prouver qu'un algorithme récursif se termine en un nombre d'appels fini. Si cette suite commence à $n$, il y aura au maximum $n$ appels récursifs.
Pile d'exécution
Illustration sur un exemple
Nous avons vu plusieurs exemple de fonctions récursives. Le but est de comprendre au niveau de la gestion de la mémoire, comment peut bien fonctionner la récursivité.
Reprenons l'exemple initial sur la fonction récursive puissance_rec vue à la fin du 1.1 (cf. lien direct) :
def puissance_rec(x: float, n: int) -> float:
if n == 0:
return 1
else:
return x * puissance_rec(x, n-1)
Vous pouvez voir ci-dessous le déroulement de l'exécution de ce code étape par étape en appuyant sur l'onglet Next >
Si l'affichage du PythonTutor n'apparaît pas ci-dessus, vous pouvez accéder directement au déroulement à cette adresse : en cliquant ici.
Il est possible de décrire ainsi la succession des étapes :
Appel à puissance_rec(2,4)
. 2*puissance_rec(2,3) = ?
. Appel à puissance_rec(2,3)
. . 2*puissance_rec(2,2) = ?
. . Appel à puissance_rec(2,2)
. . . 2*puissance_rec(2,1) = ?
. . . Appel à puissance_rec(2,1)
. . . . 2*puissance_rec(2,0) = ?
. . . . Appel à puissance_rec(2,0)
. . . . Retour de la valeur 1
. . . . 2*1
. . . Retour de la valeur 2
. . . 2*2
. . Retour de la valeur 4
. . 2*4
. Retour de la valeur 8
. 2*8
Retour de la valeur 16
On voit qu'il est nécessaire de mémoriser les paramètres et les résultats à retourner : on parle de pile d'exécution.
Une pile d'exécution permet de mémoriser des informations sur les fonctions en cours d'exécution dans un programme.
Le principe est le suivant :
-
l'instruction située en haut de la pile d'exécution est en cours d'exécution,
-
les instructions en dessous sont mises en pause dans l'attente de se retrouver au sommet de la pile d'exécution.
Voici une visualisation de ce qui se passe au niveau de la pile d'exécution lorsque l'on exécute le programme précédent :
Concrètement, ce qui est stocké à chaque étage de la pile, c'est l'adresse mémoire de l'instruction à exécuter. Pour simplifier, ici c'est l'instruction qui est écrite.
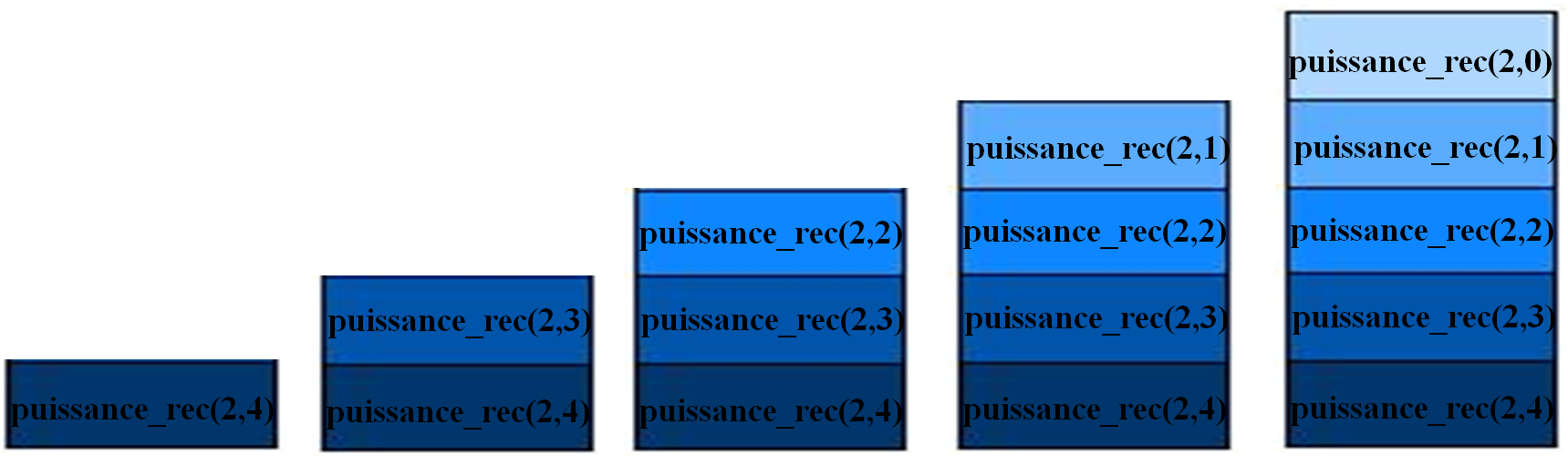
La première instruction puissance_rec(2,4) est lancée.
Comme celle-ci fait appel à puissance_rec(2,3), puissance_rec(2,3) est la nouvelle instruction exécutée tandis que
puissance_rec(2,4) est mise en pause.
De même, celle-ci faisant appel à puissance_rec(2,2), puissance_rec(2,2) est la nouvelle instruction exécutée tandis que
puissance_rec(2,3) est mise en pause.
Ces appels successifs se reproduisent conduisant à un nouvel étage de la pile d'exécution jusqu'à ce que l'instruction à exécuter devienne
puissance_rec(2,0) : il y a eu un empilement de 5 espaces-mémoire.
L'instruction puissance_rec(2,0) renvoie 1 (et clôt l'exécution de puissance_rec(2,0)).

Comme l'instruction puissance_rec(2,0) a été exécutée, elle est dépilée et l'instruction puissance_rec(2,1), qui avait mise en attente, est désormais exécuté avec la valeur renvoyée par puissance_rec(2,0).

L'instruction puissance_rec(2,1) est désormais exécutée : elle renvoie la valeur 2 puis cette instruction est dépilée ; l'instruction suivante puissance_rec(2,2) est exécutée.

On poursuit l'exécution des instructions successives en dépilant progressivement la pile d'exécution. On obtient ainsi la visualisation suivant du dépilement complet :
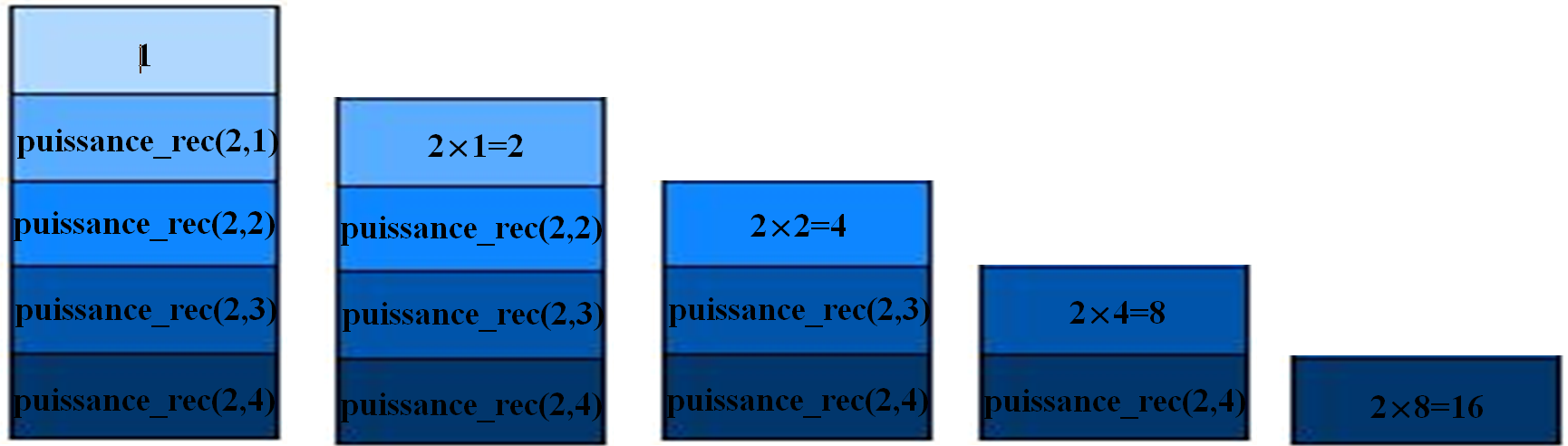
La pile d'exécution se ferme avec le renvoi de la valeur finale : 16.
Exercice
On reprend la fonction récursive de l'exemple 1 (cf. lien direct). Cette fonction récursive nb_bact renvoie le nombre de bactéries au bout de $n$ jours, $n$ étant un entier naturel saisi comme argument.
def nb_bact(n: int) -> int:
if n == 0:
return 10
else:
return 4 * nb_bact(n-1)
Sur une feuille, faire apparaître sous forme d'un schéma comme ci-dessus les différentes étapes liées à l'empilement puis au dépilement de la pile d'exécution lorsque l'on veut exécuter le code suivant :
>>>nb_bact(4)
Limitations
Reprenons l'exemple initial sur la fonction récursive puissance_rec vue à la fin du 1.1 (cf. lien direct) et dont la pile d'exécution a été illustrée dans un cas simple au 2.1 (cf. lien direct)
:
def puissance_rec(x: float, n: int) -> float:
if n == 0:
return 1
else:
return x * puissance_rec(x, n-1)
En exécutant le code suivant, vous verrez apparaître un résultat :
>>> puissance_rec(2, 981)
20437404769635530871361256581497226916530700906859085224986083762557049772738192033637969566644589579154866655684531151298277765001150399085969119214436673744076858091019117327539586267590276988750370373064129781691707499060437712782221877948907972172872918086407741866417750991158722661661540352
Si vous voyez apparaître un message d'erreur, remplacez 981 par un nombre plus petit, comme 950 ou 900.
Quelle puissance !
Par contre, en exécutant le code suivant, vous verrez apparaître, entre autres, un message d'erreur :
>>> puissance_rec(2, 982)
[...]
RuntimeError: maximum recursion depth exceeded in comparison
Le langage Python génère et gère automatiquement les espaces-mémoires de la partie dédiée de la mémoire physique de l’ordinateur : la pile d'exécution (ou pile de récursivité).
Comme tout système physique, sa capacité est limitée. Par défaut, l'implémentation de Python limite la hauteur
de la pile de récursivité à 1000.
Si l'exécution d'un appel récursif conduit à vouloir dépasser cette hauteur maximale,
alors le message d'erreur
RuntimeError: maximum recursion depth exceeded in comparison apparaît.
Il est possible de connaître et de modifier la hauteur limite de la pile de récursivité sous Python.
Pour cela, il suffit d'utiliser la bibliothèque sys qui permet de gérer, entre autres, des propriétés
du système.
Cette bibliothèque contient :
-
une fonction
getrecursionlimitqui n'a pas d'argument et renvoie la taille limite de la pile de récursivité. -
une fonction
setrecursionlimitqui admet comme argument un nombre entier correspondant à la taille limite voulue pour la pile de récursivité.
-
Déterminer la hauteur de la pile de récursivité de l'IDLE que vous utilisez pour travailler sur le langage Python en exécutant le code suivant :
import sys sys.getrecursionlimit() # utilisation de la fonction pour connaître la taille de la pile d'exécution -
Saisir le code suivant pour augmenter la pile de récursivité à 2000 (ou une valeur plus grande en mettant dans tous les cas une valeur plus grande que la taille limite trouvée avec
getrecursionlimit) :sys.setrecursionlimit(2000) # utilisation de la fonction pour limiter la taille à 2000 -
Relancer le code qui avait posé problème, normalement, vous obtenez un résultat similaire à celui ci-dessous : (si votre IDLE renvoyait un résultat pour 982, remplacer cet entier par un plus grand compris entre la taille initiale de la pile trouvée au 1. et celle modifiée imposée au 2.)
>>> puissance_rec(2,982) 40874809539271061742722513162994453833061401813718170449972167525114099545476384067275939133289179158309733311369062302596555530002300798171938238428873347488153716182038234655079172535180553977500740746128259563383414998120875425564443755897815944345745836172815483732835501982317445323323080704 -
Remettre la capacité limite à sa taille standard avec
setrecursionlimit.
-
Combien de chiffres constituent l'écriture décimale du nombre $2^{2021}$ ?
-
Même question avec $2^{3030}$.
Que préférer entre un code impératif et un code récursif ?
Tout algorithme récursif peut être transformé en un algorithme itératif.
La fonction récursive suivante qui permet de savoir si un caractère c est présent dans la chaîne de caractères ch :
def est_present(c: str, ch: str) -> bool:
if ch=="":
return False # cas d'arrêt négatif
elif c==ch[0]:
return True # cas d'arrêt positif
else:
return est_present(c,ch[1:]) # un appel récursif qui est la dernière chose à effectuer
peut facilement être réécrite en itératif en :
def est_present_iter(c: str, ch: str) -> bool:
bool = False
i = 0
while bool==False and i < len(ch):
if c==ch[i]:
bool = True
i += 1
return bool
Comme tout algorithme récursif peut être transformé en un algorithme itératif, qu'est-il préférable d'écrire ?
Quelques avantages de la récursivité :
-
La récursivité ajoute de la simplicité (de la compacité) lors de l'écriture de code, ce qui facilite le débogage,
-
La récursivité est également préférée lors de la résolution de problèmes très complexes : une solution récursive décrit comment calculer la solution à partir d’un cas plus simple, au lieu de préciser chaque action à réaliser, on décrit ce qu’on veut obtenir, c’est ensuite au système de réaliser les actions nécessaires pour obtenir le résultat demandé.
La récursivité a ses propres limites:
-
Les fonctions récursives requièrent généralement plus d’espace de mémoire.
-
Les récursions peuvent excéder la taille de la pile de récursivité : il y a alors un débordement de pile,
-
Une fonction récursive peut être de plus grande compacité dans son écriture mais n'est pas forcément de plus petite complexité (en temps d'exécution ou en espace mémoire nécessaire).
-
si on recherche l’efficacité (une exécution rapide) et si le programme peut être écrit sans trop de difficultés en itératif, on préférera l’itératif.
-
on préfère la récursivité surtout dans les situations où la solution itérative est difficile à obtenir, par exemple :
-
si les structures de données manipulées sont récursives
les arbres qui seront vus cette année dans le chapitre sd4. -
si le raisonnement lui même est récursif.
le jeu des tours de Hanoï (vu à la partie 4.3. )
-
Récursivité multiple et croisée
Récursivité multiple
Considérons la suite dite de Fibonacci.
Le problème le plus célèbre du Liber abaci est le suivant : Combien de couples de lapins aurons-nous à la fin de l'année si nous commençons avec un couple qui engendre chaque mois un autre couple qui procréé à son tour au bout de deux mois ? Cet énoncé sous-entend les conditions suivantes :
-
La maturité sexuelle du lapin est atteinte après un mois qui est aussi la durée de gestation.
-
Chaque portée comporte toujours un mâle et une femelle.
-
Les lapins ne meurent pas !!
Si on note $couple(n)$ le nombre de lapins au bout de $n$ mois, on peut modéliser le problème "pratique" par une suite $(couple(n))$. Cette suite $(couple(n))$ est définie par la relation de récurrence suivante : \begin{equation} couple(n)=\begin{cases} 1 &, \text{si $n=0$}.\\ 1 &, \text{si $n=1$}.\\ couple(n-1) + couple(n-2) &, \text{si $n>1$}. \end{cases} \end{equation}
-
Écrivez une fonction récursive
Fiboqui prend comme argument un entier naturel $n$ et qui renvoie le nombre $couple(n)$. -
Testez votre fonction récursive en exécutant
Fibo(10). Remarquez-vous quelque chose de particulier ? -
Testez votre fonction récursive en exécutant
Fibo(35). Remarquez-vous quelque chose de particulier ?
Calculez le nombre d'appels effectués pour obtenir Fibo(4).
Faire de même avec Fibo(5). Calculer le coefficient multiplicateur pour passer du nombre d'appel pour
Fibo(4) à celui pour Fibo(5).
En admettant que le coefficient multiplicateur obtenu à la question précédente reste en gros vrai quant au coût pour passer
de Fibo(n) à Fibo(n+1), déduire comment se comporte la complexité en mémoire de
cet algorithme.
L’exécution de cet algorithme récursif conduit ici à répéter des calculs, ce qui le rend vite inutilisable tel quel. Comme c'est le cas avec de nombreux algorithmes récursifs, il existe une stratégie qui cherche à modifier un tel algorithme pour éliminer les calculs redondants : on l'appelle la programmation dynamique. Elle consiste à :
-
Commencer par écrire un algorithme récursif pouvant faire des calculs redondants,
-
Stocker, dans un tableau, les résultats intermédiaires. On modifie alors l'algorithme récursif pour qu'il lise le résultat dans ce tableau s'il a déjà été calculé mais pour qu'il calcule le résultat puis le stocke dans le tableau sinon.
On gagne ainsi en complexité en temps, tout en perdant en complexité en mémoire. -
Ensuite, en analysant l'ordre des résultats appelés, il est même souvent possible d'écrire un algorithme itératif indépendant.
Nous verrons cette notion dans un chapitre dédié.
Récursivité croisée
Pour l'instant, nous avons vu qu'une fonction peut s'appeler elle-même. Il est possible qu'une fonction appelle une deuxième fonction qui la rappelle en retour.
Deux algorithmes sont dits mutuellement récursifs si l’un fait appel à l’autre et l’autre à l’un. On parle aussi de récursivité croisée.
Cette définition peut être étendue à un plus grand nombre d'algorithmes.
Voici l'exemple classique : on construit deux fonctions pair et impair qui renvoie un booléen déterminant la parité du nombre $n$ entré en argument, fonctions qui s'appellent l'une, l'autre au cours de leur
exécution.
Voici le code en python de cette imbrication :
def pair(n):
if n == 0:
return True
else:
return impair(n-1)
def impair(n):
if n == 0:
return False
else:
return pair(n-1)
-
Exécutez à la main
pair(2)en cherchant à comprendre en quoi il y a une récursivité croisée. -
Visualisez la récursivité croisée en lançant étape par étape le programme ci-dessous :
Si l'affichage du PythonTutor n'apparaît pas ci-dessus, vous pouvez accéder directement au déroulement à cette adresse : en cliquant ici.
Tours de Hanoï
De nombreux jeux peuvent être résolus grâce à des algorithmes récursifs. Un des exemples courants utilisant la récursivité est le case-tête des tours de Hanoï.
Ce casse-tête est composé de trois tours et une pile de disques rangés du plus grand au plus petit. Les disques sont initialement empilées à gauche. Il faut réussir à déplacer cette pile entièrement sur la tour de droite.

Pour cela, il faut respecter les règles suivantes :
-
ne déplacer qu'un seul disque à la fois,
-
un disque ne peut pas être posé sur un disque plus petit.
Afin de mieux comprendre le casse-tête, voici une animation venant de Wikipédia dans le cas où il y a 3 disques.
Notons TOUR_1, TOUR_2 et TOUR_3 les trois emplacements des tours, TOUR_1 étant celle de gauche par exemple.
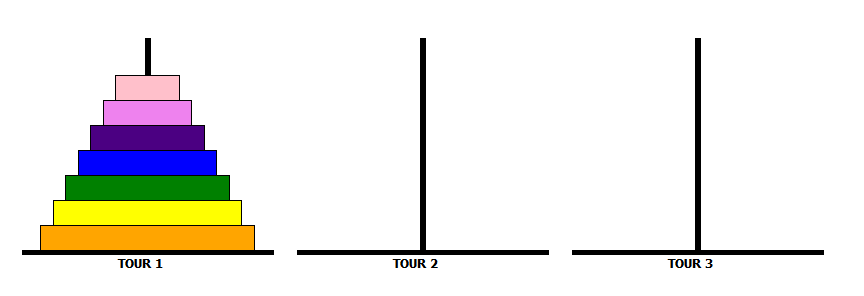
Pour déplacer une tour de $n$ disques de TOUR_1 vers TOUR_3, on effectue ces trois étapes :
-
déplacer la tour des $n-1$ premiers disques de TOUR_1 vers TOUR_2 ;
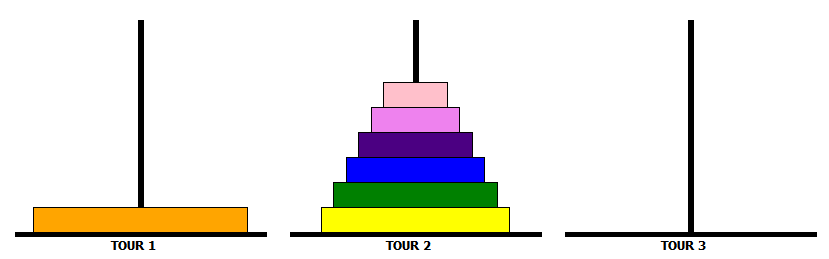
-
déplacer le plus grand disque de TOUR_1 vers TOUR_3 ;
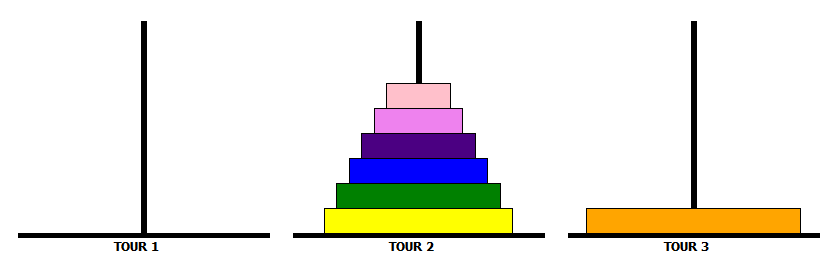
-
déplacer la tour des $n-1$ premiers disques de TOUR_2 vers TOUR_3.
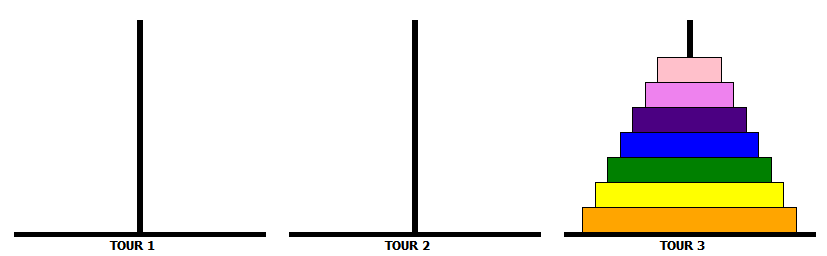
Afin de mieux comprendre le fonctionnement, vous pouvez jouer à ce jeu directement sur votre navigateur en cliquant sur ce lien.
Créez une procédure récursive hanoi(n, depart, inter, arrivee) où :
-
$n$ est le nombre de disques à déplacer,
-
departest la tour de départ ayant $n$ disques, -
interest la tour intermédiaire que l'on peut utiliser pour déplacer, -
arriveeest la tour ou doivent se trouver les $n$ disques finalement.
Cette procédure affichera une succession de phrases expliquant à chaque fois la position de la pièce à déplacer puis la
position où elle doit être déplacée.
La deuxième étape correspondra à un affichage du type :
print ("Déplacer ",...,"sur",...).
-
On peut remarquer que lorsque $n=0$, il n’y a rien à faire.
-
Traduire chaque étape de la méthode de résolution par une ligne de code.
En exécutant hanoi(3, "TOUR_1", "TOUR_2", "TOUR_3"), vous devez obtenir la sortie suivante qui correspond à
l'animation gif ci-dessus :
Déplacer TOUR_1 sur TOUR_3
Déplacer TOUR_1 sur TOUR_2
Déplacer TOUR_3 sur TOUR_2
Déplacer TOUR_1 sur TOUR_3
Déplacer TOUR_2 sur TOUR_1
Déplacer TOUR_2 sur TOUR_3
Déplacer TOUR_1 sur TOUR_3
Ce casse-tête a été inventé par le mathématicien français Édouard Lucas. Afin de mettre en valeur son jeu, il a aussi inventé une histoire fabuleuse. Il prétendit que dans le grand temple de Bénarès en Inde, centre du monde pour les hindouistes, ce dispositif du casse-tête était présent : Trois aiguilles de diamant y seraient plantées dans une dalle d'airain. Sur une de ces aiguilles, le dieu Brahma enfila au commencement des siècles, 64 disques d'or pur, le plus large reposant sur l'airain, et les autres, de plus en plus étroits, superposés jusqu'au sommet. Nuit et jour, des prêtres se succèdent pour transporter la tour de la première aiguille sur la troisième, en respectant les règles fixes vues pour le casse-tête qui auraient été imposées par Brahma. Quand tout sera fini ce sera la fin des mondes.
Ne bramez pas : "La fin du monde !" Rassurez-vous, à raison d'un déplacement par seconde, on peut montrer mathématiquement, qu'il faudrait au moins 584 milliards d'années pour pouvoir déplacer la tour de 64 disques.
L'algorithme récursif précédent est très court et assez aisé à comprendre pourquoi il fonctionne.
Il est possible d'écrire des algorithmes itératifs qui affichent aussi la succession des déplacements à effectuer. Cependant, leur écriture est plus compliquée, plus longue et il est plus difficile à comprendre pourquoi ils fonctionnent correctement. Si vous voulez en découvrir, Wikipedia en proposent 3 : lien.
Exercices
Notion de récursivité
Écrire une procédure récursive qui demande un nombre positif à l’utilisateur et qui affichera ce nombre que s’il est positif. Sinon, demander à l’utilisateur de recommencer.
Notion de récursivité
Vous avez déjà beaucoup travaillé avec la fonction puissance_rec qui renvoie $x^n$.
def puissance_rec(x: float, n: int) -> float:
if n == 0:
return 1
else:
return x * puissance_rec(x, n-1)
Le but est de créer une fonction récursive somme_puissance_rec qui permet d'obtenir la somme $1+x^1+x^2+...+x^{n-1}+x^n$, sachant que $x$, un réel, et $n$, un entier naturel, sont deux arguments de cette fonction.
Créez une telle fonction somme_puissance_rec qui est récursive et qui peut aussi faire appel à la fonction puissance_rec.
Notion de récursivité
Dans le sud champardennais, un espace protégé Natura 2000 possède une faune d'insectes remarquables, en particulier un papillon appelé le
"fadet des tourbières".
Comme cette espèce de papillon est désormais considérée comme menacée en France, l'espace protégé cherche à y maintenir, voire à y développer la population de ce cette espèce grâce à un dispositif mis en place à partir de 2020.
En 2020, la population de fadets des tourbières est estimée à 150 individus dans l'espace protégé.
On note $nb\_fadet(n)$ la population de papillon de cette espèce vivant dans l'espace protégé $n$ années après 2020.
Les écologues responsables du dispositifs espèrent que chaque année 80% de la population précédente reste et que 50 individus s'installent dans l'espace protégé.
On peut donc écrire cette relation ainsi : $nb\_fadet(n+1)=0.8
\times nb\_fadet(n)+50$.
-
En admettant cette relation, proposez une fonction recursive
nb_fadetqui prend comme argument l'entier naturel $n$ et renvoie la population $nb\_fadet(n)$ estimée pour l'année $2020+n$. -
Au vu du modèle, peut-on espérer une sauvegarde de l'espèce dans la zone protégée ?
Condition d'arrêt
Le but est de créer une fonction récursive qui renvoie le nombre d’occurrences d’un caractère donné $c$ dans une chaîne de caractères donnée $ch$, $c$ et $ch$ étant donné comme arguments.
-
Expliquer comment on peut connaître le nombre d'occurrences du caractère $c$ dans la chaîne $ch$ si on connaît le premier caractère de la chaîne ainsi que le nombre d'occurrences du caractère $c$ dans la chaîne $ch$ où le premier élément a été enlevé.
-
Proposer une fonction récursive
nb_occurrencequi répond au cahier des charges précédents.-
Utiliser des préconditions sur les arguments saisis.
-
Vous pouvez utiliser le fait que
ch[1:]correspond à la chaîne de caractères $ch$ privée du premier caractère, chaîne éventuellement vide.
-
Notion de récursivité
SD1 et SD3.
Voici un script :
vide = []
def mystere(t: int, q: list):
if q == vide:
return [t]
else:
return [t] + [mystere(cle(q), champ2(q))]
def est_vide(l: list) -> bool:
return l == vide
def cle(l: list) -> int:
assert not est_vide(l), "La structure mystère vide n'a pas de clé"
return l[0]
def champ2(l: list) -> int:
assert not est_vide(l), "La structure mystère vide n'a pas de champ2"
return l[1:]
def affiche(l) -> None:
print(cle(l))
-
Parmi les fonctions définies dans le script, déterminer celle(s) étant récursive(s).
-
Tester la fonction
mystereafin de déterminer le nom d'une structure de données abstraites dont le script précédents peut être vu comme une interface.
Pile d'exécution
Le mathématicien Lothar Collatz a inventé il y a près d'un siècle la suite mathématique suivante : Prendre un nombre entier au hasard. S'il est pair le diviser par 2, sinon,
le multiplier par 3 et ajoutez 1. Répéter ensuite l'opération.
Cette suite peut être écrite mathématiquement par la relation de récurrence suivante : \begin{equation} u_{n+1}=\begin{cases} \frac{u_n}{2} &,
\text{si $n$ est pair}.\\ 3 \times u_{n} +1 &, \text{si $n$ est impair}. \end{cases} \end{equation}
Collatz puis de nombreux mathématiciens ont cherché à prouver que quel que soit le nombre de départ choisi, on arrivera à la valeur 1 donc à la répétition infinie 4, 2, 1. Ce résultat non encore démontré est appelée conjecture de Syracuse
Cette conjecture mobilisa tant les mathématiciens durant les années 1960, en pleine guerre froide, qu'une plaisanterie courut selon laquelle ce problème faisait partie d'un complot soviétique visant à ralentir la recherche américaine.
-
Proposez une fonction récursive
syracusequi prend en paramètre un entier naturel $n$ et qui renvoie la liste de toutes les valeurs prises par la suite jusqu'à atteindre la valeur 1.-
Vous testerez votre fonction
Syracuseavec $n=15$ entre autres et vous devez obtenir l'affichage suivant :>>>syracuse(15) [15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] -
Vous pourrez utilisez la méthode
extend:liste1.extend(liste2)permet de rajouter en fin deliste1tous les éléments de la listeliste2.
-
On appelle temps de vol le plus petit indice $p$ tel que $u_p=1$.
Proposez une fonction temps_vol qui prend en paramètre un entier $n$ et qui renvoie le premier indice où la suite de Syracuse prend la valeur 1 si on part de la valeur $n$.
Vous testerez votre fonction temps_vol avec différentes valeurs de $n$ puis avec le nombre 12235060455 ; que se passe-t-il dans ce dernier cas ?
Fixez la taille de la pile de récursivité à 2000 afin d'obtenir le temps de vol de 12235060455. Vu le résultat affiché expliquez pourquoi il est nécessaire d'augmenter la taille de la pile.
Comme on ne sait toujours pas si toute suite de Syracuse repasse par la valeur 1 à un moment des itérations, on ne sait pas si la fonction que vous avez écrite au 1. se termine quel que soit le nombre entier saisi en entrée.
Ceci est un exemple du fait qu'il peut être très difficile (voire impossible si ce problème est réellement indécidable ?) de prouver qu'un
programme récursif se termine ou non.
Récursivité multiple
François Viète a démontré en 1592 que l'on pouvait approcher le nombre $\pi$ grâce deux suites imbriquées $(u_n)$ et $(v_n)$ définies respectivement par :
\begin{equation} \begin{cases} u_0=\sqrt{2}\\ u_{n+1} = \sqrt{2+u_{n}}, \text{si $n \geqslant 0$}. \end{cases} \begin{cases} v_0=2\\ v_{n+1} = v_n \times \frac{2}{u_{n}}, \text{si $n \geqslant 0$}. \end{cases} \end{equation}En effet, François Viète a démontré que les valeurs de la suite $(v_n)$ se rapprochent infiniment près de $\pi$ lorsque les valeurs de $n$ deviennent infiniment grande.
-
Écrivez une fonction récursive
uqui renvoie le terme $u_n$, où $n$ est entré comme paramètre. -
Écrivez une fonction récursive
vqui renvoie le terme $v_n$, où $n$ est entré comme paramètre. -
Obtenez une valeur proche de $\pi$ à l'aide de votre fonction
v.
Notion de récursivité
Proposez une fonction récursive mon_minimum qui donne l'élément le plus petit d'une liste non vide d'entiers.
Le minimum d'une liste vide n'est pas défini.
Notion de récursivité
Pour convertir un nombre entier positif $n$ de la base décimale à la base binaire, il suffit d'effectuer des divisions successives du nombre $n$ par 2. La liste des restes des divisions constituent la représentation binaire.
Écrire une fonction récursive dec_vers_bin renvoyant la liste donnant une représentation binaire d’un nombre $n$ saisi comme argument.
Vérifier la fonction écrite avec ces tests :
-
dec_vers_bin(0)renvoie la liste[0]. -
dec_vers_bin(13)renvoie la liste[1, 1, 0, 1]. -
dec_vers_bin(346)renvoie la liste[1, 0, 1, 0, 1, 1, 0, 1, 0].
Rappel !
La factorielle d'un entier naturel $n$ non nul, notée $n!$, est le produit de tous les nombres entiers compris entre 1 et $n$, c'est-à-dire : $n!=1 \times 2 \times ... \times (n-1) \times n$.
Il existe une relation "simple" entre $n!$ et $(n-1)!$.
En effet : $n!=1 \times 2 \times ... \times (n-1) \times n = \underbrace{1 \times 2 \times ... \times (n-1)}_{(n-1)!} \times n = (n-1)! \times n$,
En sciences, la fonction exponentielle est très importante. On admet que la valeur de cette fonction en 1 est notée $e^1$ et que sa valeur peut être vue comme égale à la somme infinie : $1 + \frac{1}{1!} + \frac{1}{2!} + ... + \frac{1}{n!} + ... $, où $n$ va tendre vers $+\infty$.
-
Écrivez une fonction récursive
inv_factqui prend comme argument l'entier non nul $n$ et qui renvoie $\frac{1}{n!}$ : -
Quelle est la condition d'arrêt de votre fonction récursive ?
-
Pourquoi pouvez-vous être certain.e.s que la situation de terminaison sera atteinte après un nombre fini d'appels récursifs ?
-
Écrivez une procédure qui affiche une valeur approchée de $e^1$ sachant que $e^1 \simeq 1 + \frac{1}{1!} + \frac{1}{2!} + ... + \frac{1}{25!}$.
Proposer une fonction récursive extraire_pairs qui prend en paramètres une liste de nombres entiers et qui
renvoie la liste formée des nombres pairs de la liste initiale sans modifier l'ordre.
Voici un exercice à faire en autonomie pour tester votre maîtrise de
la récursivité tout en retravaillant la dichotomie.
Cet exercice est proche d'un exercice 2 d'un sujet de l'épreuve pratique.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice dans sa version récursive à compléter.
Voici un exercice à faire en autonomie pour tester votre maîtrise de
la récursivité tout en retravaillant les tableaux 2D.
Cet exercice est proche d'un exercice 2 d'un sujet de l'épreuve pratique.
Cet exercice est issu du site collaboratif de la forge.
Cliquer sur ce lien pour accéder à l'exercice dans sa version récursive à compléter.
Basculer dans l'éditeur vers la "Version à trous sans boucle" si le lien ne
le fait pas directement.
Exercices du baccalauréat
Exercices de renforcement
On rappelle qu'un nombre entier compris entre 0 et 127 peut être codé sur 8 bits. Voici une fonction mystère nommée myst2 qui prend en argument une liste d'entiers naturels compris entre 0 et 127 :
def myst2(l: list) -> int:
if l==[]:
return 0
else:
l.pop(0) # on supprime le premier élément de la liste l
return 8 + myst2(l)
-
Pourquoi cette fonction
myst2est une fonction récursive ? -
Testez cette fonction avec quelques listes, dont
[3],[127],[3,7],[3,100,75,7,0]. -
Quel est le rôle de cette fonction
myst2?
-
La fonction
myst2est une fonction récursive cqr elle s'appelle elle-même lors du dernierreturn. -
myst2([3]) , myst2([127]) , myst2([3,7]), myst2([3,100,75,7,0])renvoie
(8, 8, 16, 40). -
Le rôle de cette fonction
myst2est de renvoyer le nombre total de bits pour stocker l'intégralité des nombres entiers de la liste.
-
Écrivez une fonction récursive
sommequi prend comme argument un entier non nul $n$ et qui renvoie la somme de tous les nombres entiers compris entre 1 et $n$. -
Quelle est la condition d'arrêt de votre fonction récursive ?
-
Pourquoi pouvez-vous être certain.e.s que la situation de terminaison sera atteinte après un nombre fini d'appels récursifs ?
-
Rajouter une précondition.
-
Fonction récursive
sommequi prend comme argument un entier non nul $n$ et qui renvoie la somme de tous les nombres entiers compris entre 1 et $n$ :def somme(n: int) -> int: if n == 1: return 1 else: return n + somme(n-1)La condition d'arrêt correspond au cas le plus simple $n=1$ : il suffit de renvoyer 1 en tant que somme totale.
Pour le cas général, il suffit de remarquer que pour calculer une somme, il suffit de rajouter la valeur du dernier terme à la somme partielle des $n-1$ premiers termes.
-
La condition d'arrêt de votre fonction récursive est ici
n == 1. -
La suite avec l'entier $n$ est une suite strictement décroissante lors des appels récursifs, on peut donc être certain.e que la situation de terminaison sera atteinte après un nombre fini d'appels récursifs.
-
Il suffit de rajouter une précondition permettant de s'assurer que l'argument saisi est bien un entier non nul.
def somme(n: int) -> int: assert type(n) == int and n > 0, "Veuillez saisir une nombre entier naturel non nul." if n == 1: return 1 else: return n + somme(n-1)
On considère désormais que les couples de lapins sont mortels : les lapins sont tués lors de leur quatrième mois.
Si on note $l_n$ le nombre de couples lapins au bout de $n$ mois, on peut modéliser le problème "pratique" par une suite $(l_n)$. Cette suite $(l_n)$ est définie par la relation de récurrence suivante : \begin{equation} l_n=\begin{cases} 1 &, \text{si $n=0$}.\\ 1 &, \text{si $n=1$}.\\ 2 &, \text{si $n=2$}.\\ 3 &, \text{si $n=3$}.\\ l_{n-1} + l_{n-2} - l_{n-4} &, \text{si $n>3$}. \end{cases} \end{equation}
-
Écrivez une fonction récursive
couplesqui prend comme argument un entier naturel $n$ et qui renvoie le nombre de couples de lapins $l_n$ -
Déterminer le nombre de couples de lapins vivants au bout de 24 mois, soit 2 ans.
-
Il y a plusieurs conditions d'arrêt pour cette fonction récursive
couples: les quatre cas simples connus pour $n$ allant de 0 à 3.def couples(n: int) -> int: if n == 0: return 1 elif n == 1: return 1 elif n == 2: return 2 elif n == 3: return 3 else: return couples(n-1) + couples(n-2) - couples(n-4) -
couples(24)renvoie 1431. Un couple donnerait ainsi 1431 couples dans ces conditions au bout de 2 ans malgré l'exécution des couples âgés de 4 mois.
Écrire une procédure récursive qui demande à l’utilisateur un nom commençant par la lettre 'c' et qui affichera ce nom que si la chaÎne de caractères commence bien par 'c'. Sinon, demander à l’utilisateur de recommencer.
La condition d'arrêt est ici le cas où la saisie est correcte.
Le cas général correspond au cas où la saisie est incorrecte.
def entrer_nom() -> None:
ch = input("Entrez un nom")
if ch[0] == 'c':
print("Vous avez saisi comme nom",ch)
else:
print("Recommencez, le nom saisi doit commencer par le caractère 'c' (minuscule).")
return entrer_nom()On note $tortue(n)$ la population de tortues d'une île $n$ années après 2021.
On admet que la population de tortues en 2021 est de 186 et l'évolution projetée de la population est telle que $tortue(n)$ vérifie la relation suivante :
\begin{equation} tortue(n)=\begin{cases} 186 &, \text{si $n=0$}.\\ 0.9 \times tortue(n-1) + 10 &, \text{si $n>0$}. \end{cases} \end{equation}
-
En admettant cette relation, proposez une fonction recursive
tortuequi prend comme argument l'entier naturel $n$ et renvoie la population $tortue(n)$ estimée pour l'année $2021+n$. -
Au vu du modèle, que penser de la population de tortues à la fin du siècle ?
-
La condition d'arrêt correspond à l'année 2021.
def tortue(n: int) -> float: if n == 0: return 186 else: return 0.9 * tortue(n-1) + 10 -
tortue(79)renvoie environ 100.02.
Ainsi, la population de tortues à la fin du siècle sera de 100 individus suivant ce modèle.
Sitographie
Voici une liste de sites traitant de la récursivité en python :
- cours sur openclassrooms
- cours concis sur la récursivité mais assez complet
- Différents exercices sur la récursivité en Python
Voici une video sur le site lumni qui traite de la récursivité : une-introduction-a-la-recursivite
Savoir faire et Savoir
- Écrire la condition d'arrêt d'une fonction récursive,
- Écrire une programme récursif,
- Analyser le fonctionnement d'un appel récursif,
- Comprendre l'empilement et le dépilement des appels au niveau de la pile d'exécution,
- À terme : Décomposer un problème compliqué en un ou plusieurs sous-problèmes du même type pour le le résoudre par la récursivité.
- La notion de récursivité,
- La notion de pile d'exécution.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International