Présentation de Python
Demandez le programme !
Un première entrée par de l'algorithmique
Une manière d'amener la pratique de python est de partir de situations algorithmiques simples avec des tableaux d'exécutions.
Voici quelques exemples simples :
1 x←-2 2 y←-1 3 z←x-y
Faire un tableau d'exécution.
On peut proposer un tableau à compléter ou demander à construire le tableau. La construction du tableau oblige à recenser les variables de l'exercice.
| ligne 1 | ligne 2 | ligne 3 | |
|---|---|---|---|
| x | |||
| y | |||
| z |
Un grand classique.
1 x←-1 2 y←-1 3 x←y 4 y←x
| ligne 1 | ligne 2 | ligne 3 | ligne 4 | |
|---|---|---|---|---|
| x | ||||
| y |
1. x ← 0 2. y ← -1 3. si x < y alors 4. x ← x+y 5. sinon 6. y ← x-y
- Faire la trace d'exécution de cet algorithme.
- Recommencez avec x=-2 et y=-1
On peut proposer de prolonger l'exercice par le codage en langage python :
1. x ← 0 2. y ← -1 3. z ← 1 4. si x < y alors 5. si y<z alors 6. z←x+y+z 7. sinon 8. z←x+y-z 9.sinon 10. si y<z alors 11. z←x-y+z 12. sinon 13. z←x-y-z
Faire un tableau d'exécution.
En mathématiques, le tableau d'exécution à un aspect "horizontal" (les variables sont indiquées sur les lignes). En NSI, le tableau d'exécution à généralement un aspect plus "vertical" avec une numérotation des lignes de l'algorithme.
Voici une vidéo d'une trace d'exécution, d'un exercice de recherche de palindrome, réalisée en NSI.
Les différentes manières d'utiliser Python
On peut programmer avec Python de plusieurs manières :
- EduPython : logiciel libre installé sur les ordinateurs de la région. Le programme de SNT fait mention de l'usage de Python. Accès direct à Edupython
- Jupyter : logiciel qui s'installe via la suite de logiciels Anaconda ou bien via EduPython 2.7. C'est un logiciel à privilégier pour réaliser des présentations interactives. Une vidéo qui permet d'utiliser Jupyter à partir d'EduPython. Cette vidéo commence par la désinstallation de la version précédente d'EduPython
- En ligne de commande après avoir installé Python 3.6.
Il existe aussi des consoles en ligne.
- Une console interactive
- La console du manuel DELAGRAVE
- Une application intéressante "repl.it"
- Un IDE sur le site
Les bases de Python : console, variable, print, input et maths.
Un diaporama de présentation de Python : ici
Version pdf embarquée :
Aspect général d'EduPython
Pour compiler et exécuter un programme, il faut utiliser la touche  .
.
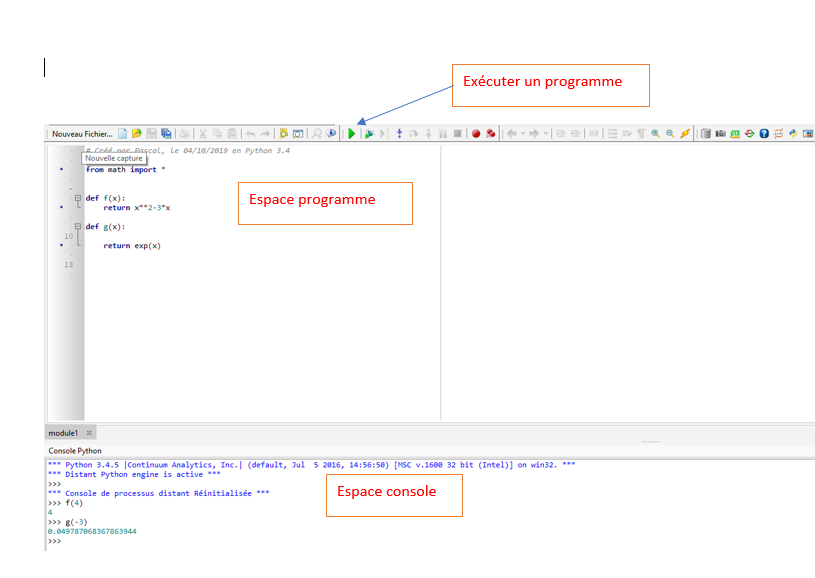
La console
Le mode console se repère facilement avec les symboles>>> devant l'instruction.
Le but est d'ouvrir le logiciel EduPython et/ou le logiciel Jupyter afin de copier-coller les codes proposés. Attention : ne pas copier-coller les symboles >>>
Une vidéo de présentation de la console et d'EduPython. Cette vidéo commence par l'installation d'EduPython.
L'affectation
Par exemple, on veut stocker le nombre 5 dans une variable notée x. Nous avons noté en pseudo-code ceci :
Ceci signifie : « à l’adresse mémoire référencée par x - autrement dit, dans la boîte aux lettres dénommée x -, se trouve la valeur 5 ». Nous utilisons plus fréquemment l’abus de langage « la variable x vaut 5 ».
En langage Python, l'affectation sera notée à l'aide du symbole égal : =. On note ainsi l'affectation de 5 à x :
x = 5
L'instruction (en mode console) de cette affectation s'écrit donc :
>>>x = 5Attention ! En écrivant ceci, on n'exprime pas une égalité mais l'interpréteur exécute les actions suivantes :
-
il définit un identificateur
xcomme une nouvelle variable, -
il réserve un espace mémoire pour cette variable,
-
il associe à cette variable un entier dont la valeur est 5,
xest dès lors une variable de type entier.
Ainsi, en python, on peut lire x=5 comme : "x est lié à un objet de type int dont la valeur est 5".
Les entrées-sorties : affichage et saisie
La fonction print permet d'afficher les éléments mis entre parenthèses.
input
La fonction input permet d'obtenir une saisie depuis le clavier.
Attention ! La fonction input renvoie toujours une chaîne de caractères (son type est bien str) même si un nombre (entier ou réel) a été saisi. Pour pouvoir utiliser le renvoi dans un calcul, il est parfois
nécessaire de changer son typage à l'aide des fonctions int ou float qui permettent de transformer respectivement une chaîne de caractères correspondant à un nombre en nombre entier ou nombre réel (un flottant
pour être précis).
Tester le code suivant :
>>>a=input("Entrer un nombre")
>>>b=a*10
>>>print(b)
Pourquoi cet affichage ?
Tester la code suivant (qui vous permet de connaître le type en python)
>>>type(a)Transformer votre code de la manière suivante :
>>>a=int(input("Entrer un nombre"))
>>>b=a*10
>>>print("Votre nombre multiplié par 10",b)
float à la place de int. Vous pouvez vérifier vos types avec typeFaire quelques tests
Quelques commandes
En quelques commandes, un petit tour dans la console.
>>>print("hello world ! ")Quelques exemples d'affectation de variables en mode console
L'instruction (en mode console) :>>>x = 2= est utilisé pour affecter des valeurs aux variables
>>>print(x)Remarquez l'absence de " ". Testez les lignes suivantes :
>>>x = "Hello world ! "
>>>print("x ")
>>>print(x)>>>x = x+1>>>x+=1Sous python, on peut affecter une valeur à plusieurs variables simultanément :
>>>a,b=2,3
>>>a
>>>bFaire des maths avec Python en console
Faire le test suivant :
>>>sqrt(2)Vous devez obtenir un message d'erreur car Python ne connait pas la commande sqrt().
Maintenant, tester ceci :
>>>from math import *
>>>sqrt(2)
La fonction carrée et un calcul d'image.
>>>def f(x):
.... return x**2
>>>f(2)Les scripts, les fonctions
import
A partir de cette section, vous devez écrire vos programmes dans l'espace des scripts et utiliser le symbole  pour exécuter vos programmes.
pour exécuter vos programmes.
Importation systématiques des librairies utiles et encodage:
On peut ainsi utiliser directement les fonctions mathématiques et aléatoires de base ainsi que faire des graphiques avec une syntaxe aussi légère que possible tout en étant compatible avec la littérature sur le sujet. La ligne avec coding: utf-8 -*- permet d'éviter des soucis avec les caractères accentués.
Commencer tous vos programmes par cette série d'imports :
# -*- coding: utf-8 -*-
from math import *
from random import *
import matplotlib.pyplot as plt
import numpy as np
Les fonctions
En Python une fonction est définie par l'instruction composée def suivie du nom de la fonction et se termine obligatoirement par deux points : puis le bloc d'instructions qu'il ne faut pas oublier d'indenter.
Une fonction est utilisée comme une instruction quelconque. Dans le corps d'un programme, un appel de fonction est constitué du nom de la fonction suivi de parenthèses.
La notion de fonction en informatique relève du même concept qu'une fonction mathématiques, c'est-à-dire qu'on définit une fonction puis on l'applique à différentes valeurs.
def carree(a) :
" "" Fonction permettant de renvoyer le carré du nombre a qui est en paramètre "" "
return a**2 # renvoie l'image de a par la fonction carree
Vous remarquerez le symbole : très important en Python qui marque le début d'un bloc.
C'est l'indentation qui délimite le bloc d'instructions.
Lorsqu'on définit la fonction carree(), a est appelé
paramètre de la fonction. Lorsqu'on appelle la fonction avec une valeur explicite pour a, comme dans
carree(3), on dira plutôt que 3 est un
argument de la fonction.
En appelant la fonction carree() d'argument 3, on obtient 9
-
La fonction est autodocumentée par un texte :
" "" Ecrire ici la description "" "(c'est ce que l'on appelle le docstring de la fonction).Le
docstringd'une fonction permet de donner des informations sur la fonction et le lien entre les entrées et la sortie (en d'autres termes, le rôle de la fonction).Quant on saisit dans la console, après l'exécution de la fonction, l'instruction
help(nom de la fonction), Python affiche le docstring de la fonction ce qui nous permet d'avoir des informations sur la fonction en cas d'oubli.>>> help(carree) Help on function carree in module __main__: carree(x) Fonction permettant de renvoyer le carré du nombre x qui est en paramètre -
La fonction se termine avec une instruction
return. Ce qui suit lereturnest l'image des entrées par la fonction. Dès que la fonction rencontre unreturn, elle renvoie ce qui suit lereturnet stoppe son exécution. Commentaire: le symbole#apparaîtra à maintes reprises. Il marque le début d’un commentaire que la fin de la ligne termine. Autrement dit, un commentaire est une information aidant à la compréhension du programme mais n’en faisant pas partie.
Différence entre fonction et procédure.
Une fonction renvoie une valeur et une procédure ne renvoie rien. Le langage Python ne fait pas la différence entre les deux, il utilise l'instruction def pour les deux. Par contre l'instruction
return n'est pas obligatoire dans le cadre d'une procédure.
Il est conseillé d'écrire return None dans le cadre d'une procédure, mais ce n'est pas une obligation.
Tester le programme suivant :
def affichage(mot1,mot2):
print(mot1,mot2)
affichage("maths ","Python ")
Transformer cette procédure en ajoutant return None à la fin de la fonction
affichage . Tester la procédure.
Chercher l'erreur ( il y a une erreur à corriger).
def carre(x):
return x**2
print(carre(1.7))
Chercher l'erreur ( il y a une erreur à corriger).
def quotient(x,y)
return x/y
Ecrire une procédure qui prend en entrée deux variables nb1 et nb2 et qui affiche la moyenne des deux variables.
Ecrire une fonction moyenne(nb1,nb2) qui a pour paramètres deux variables de type float et qui renvoie la moyenne de ces deux nombres.
Ecrire une fonction vitesse(d,t), qui a pour paramètres deux variables de type float correspondant la distance d en mètre et le temps de parcours t en seconde et qui renvoie la vitesse en m/s.
-
Limiter les variables intermédiaires
Utiliser une écriture qui correspond aux notations mathématiques $$f:x \mapsto 2x+3$$ Limiter le recours aux variables intermédiaires c'est utiliser davantage la notation fonctionnelle qui correspond aux notations du cours de maths
# Au lieu d'utiliser cette forme : def f1(a,b): c=a**2+b**2 return c # Utiliser cette forme def f(a,b): return a*a+b*b -
Privilégier une version fonctionnelle à une version procédurale.
Un grand classique : les racines d'un trinôme.
Les structures conditionnelles
Un programme doit souvent prendre en compte différents cas et s'adapter à différentes situations.
Il est alors nécessaire d'écrire des conditions, c'est-à-dire des expressions logiques dont le résultat est soit "Vrai " soit "Faux ".
Voici comment s'écrit la structure conditionnelle en python :
if condition :
instruction(s)
else :
instruction(s)
Vous remarquerez le symbole : très important en Python qui marque le début d'un bloc.
C'est l'indentation qui délimite le bloc d'instructions
Dans le cas où la condition est fausse, on peut donner des instructions à l'aide de la commande
else .
def egaliteFrac(frac1,frac2):
nb1 = frac1[0]*frac2[1] #on calcule a*d
nb2 = frac1[1]*frac2[0] #on calcule b*c
if nb1 == nb2:
test = True
else:
test = False
return test
egaliteFrac([1,2],[-20,-40])
La structure elif :
if condition1 :
instruction(s)
elif condition2 :
instruction(s)
elif condition3 :
instruction(s)
else :
instructions
a=float(input("Entrer un nombre : "))
if a>0 :
print("Vous avez entré un nombre strictement positif. ")
elif a==0 :
print("Vous avez entré un nombre nul. ")
else :
print("Vous avez entré un nombre strictement négatif. ")
Il est possible d'utiliser plusieurs conditions en utilisant les connecteurs logiques AND et OR.
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=|x-3|$.
Ecrire une fonction f(x) qui prend en paramètre une variable de type float et qui renvoie un objet de type float correspondant à l'image de $x$ par $f$.
On n'utilisera pas la fonction abs(x) correspondant à $|x|$.
Abonnement et réseau social
Niveau : accessible
Inspiré du programme de SNT
" Un abonnement sur un réseau social de vidéo coûte 9.99 € par mois avec trois mois d 'essai gratuit pour une seule personne ou 15.99 € avec 1 mois d'essai gratuit pour toute la famille ".
Compléter la fonction suivante qui a pour argument le nombre de mois et qui renvoie le prix à payer.
def prix(mois):
abonnement=input("Abonnement ? : seul ou famille ? ")
# faire afficher "abonnement minimal d 'un an" si le nombre de mois est inférieur à 12
# ...
return(prix)
Tester la fonction avec :
print(prix(12))
Vous devriez observer :
Abonnement ? : seul ou famille ? seul 89.91
Une vidéo qui donne offre une autre présentation :
Les boucles bornées - for
La boucle pour est utilisée quand on connaît le nombre de fois où l'on doit répéter une suite d 'instructions.
Parcours sur les index
Dans un premier temps l'attribut dans range sera un entier, nous verrons dans la suite qu'il peut en être autrement.
for i in range(n):
...
les différentes instructions à répéter
...
Il y a ainsi trois possibilités pour utiliser l'instruction range, suivant le nombre de
paramètres entiers saisis :
-
for i in range(n):le compteur $i$ va de 0 à $n-1$ par pas de 1 : il y a donc bien $n$ répétitions.
-
for i in range(m,n):le compteur $i$ va de $m$ à $n-1$ par pas de 1 : il y a donc $n-m$ répétitions. Ici, on a forcément $n\geq m$.
-
for i in range(m,n,pas):le compteur $i$ va de $m$ à $n-1$ par pas de $pas$ ; le pas est un entier relatif non nul, il peut en particulier être négatif.
Pour illustrer cette structure nous allons partir sur un premier exemple : obtenir la somme des n premiers entiers naturels. Pour n=4, on veut écrire un programme qui renvoie la valeur de 0+1+2+3=6.
La première ligne fait que la suite du code va être répétée n fois en incrémentant de manière automatique la variable i de 0 à n-1.
def somme(n): #les int sont ici pour indiquer le typage des variables d'entrée et de sortie. Ici l'attribut est de type int et la sortie également
"""""La fonction somme renvoie la somme des n-1 premiers entiers naturels.
la fonction somme a pour attribut un entier (int) : n et renvoie un autre entier :S
Pour n=4 : S=0+1+2+3=6"""""
S=0 #initialisation de la somme à 0
for i in range(n):
S=S+i
return S
somme(4) # Penser à faire un print(somme(4)) si vous voulez un affichage
Pour voir l'exécution du code, un site intéressant : "python tutor" (abordé un peu plus loin sur le site)
On donne une suite $u_{n}$ définie par sa relation de récurrence :
$\left\{ \begin{array}{ll} u_{n+1} = \frac{u_n + 1}{u_n-2}\\ u_0=1 \end{array} \right.$Ecrire une fonction u(n) qui a pour argument une variable n de type int et qui renvoie le terme d'indice $n$ de la suite $u$.
Parcours sur les éléments
Dans la partie précédente, l'instruction range(m,n) créé un ensemble de nombres dont le
compteur i parcourait les valeurs.
Un tel ensemble dont un peut parcourir les valeurs avec une boucle for est appelé un itérable.
Il existe de nombreuses structures de données itérables :
-
Une chaîne de caractères (type
str) est un itérable, -
Une liste (type
list) est un itérable, -
Un dictionnaire (type
dict) est un itérable (abordé dans la formation python 2),
En Python, pour utiliser un itérable dans une boucle for, il suffit d'utiliser le mot-clé
in. Voici la structure générale :
for elt in iterable:
instruction 1
instruction 2
...
Dans cette boucle, elt va parcourir les éléments de la iterable.
Le programme ci-dessous affiche séparément chaque caractère d'une chaîne de caractères :
# -*- coding: utf-8 -*-
ch="Bonjour à tou.te.s"
for elt in ch:
print(elt)Le but est compter le nombre de 'e' dans une phrase.
def nbre_de_e(phrase):
compteur=0
for lettre in phrase:
if lettre=="e":
compteur=compteur+1
return compteur
print("Le nombre de e est :",nbre_de_e("hello world!"))
Transformer l'algorithme pour qu'il compte le nombre de voyelles.
Simulation du lancer d'un dé
from random import randint # on importe le module randint de random
liste=[randint(1,6) for i in range(1000)]
print(liste)
Utiliser le code de l'exercice précédent pour compter le nombre de 1 de la liste.
Une vidéo sur les boucles for :
Les boucles non bornées - while
Ces boucles, aussi appelées boucles "Tant que" ou boucles "While" effectuent les instructions situées dans le corps de la boucle tant qu'une condition est vérifiée. En langage Python, la syntaxe est la suivante :
while condition_est_vraie:
instruction 1
instruction 2
A l'instar des structures conditionnelles (si alors sinon) et des boucles bornées (pour), le corps de la boucle est constitué d'instructions indentées.
Cas général : nombre d'itérations non connu :
On utilise cette boucle lorsque l'on ne sait pas à l'avance combien de fois seront effectuées les instructions du corps de la boucle. Cela peut être lié à la valeur d'une ou de plusieurs variables dont la valeur évolue, parfois à cause de la décision de l'utilisateur.
Les suites offrent de nombreuses situations.Algorithme de seuil
On donne une suite $u_{n}$ définie par sa relation de récurrence :
$\left\{ \begin{array}{ll} u_{n+1} = 3u_n + 1\\ u_0=2 \end{array} \right.$On cherche l'indice $n$ tel que $u_{n} \ge 300 $
On a l'algorithme en pseudocode suivant :
u ← 0 n ← 0 tant que u < 300 faire n ← n+1 u ← u+1
Cet algorithme donne le programme suivant :
from math import *
u=0
n=0
while u <300:
n=n+1
u=3*u+1
print(n, u)
Longueur de courbe
Pour obtenir l'approximation de la longueur d'une courbe représentative d'une fonction $f$ sur un intervalle $[a;b]$. On peut découper $[a;b]$ en $n+1$ intervalles et ajouter les longueurs des $n+1$ segments d'extrémitées $A(x_n,f(x_n))$ et $B(x_{n+1},f(x_{n+1}))$
Ecrire une fonction long(f,a,b,nb) qui renvoie l'approximation de la longueur de la courbe représentative de $f$ sur l'intervalle $[a;b]$ avec nb intervalles.


Une vidéo de présentation des boucles while :
Et une autre :
Aspect général de jupyter
Un aperçu d'un fichier jupyter.
Observer le déroulement d'un programme en Python
Pour observer l’exécution d’un programme, nous pouvons utiliser une application web : pythontutor
Une vidéo présentant le fonctionnement de pythontutor :
D'autres programmes et activités.
Algorithme de dichotomie
Téléchargements des fichiers :
Le jeu des 8 erreurs
Les 8 erreurs
Retrouver les 8 erreurs dans ce code :
def makeList(deb,fin,max)
lst==[]
s=0
while s<max
a=randint(deb,fin)
lst.randint(a);
s=s+a
return lst,a
Jeu inspiré de l'algorithme de l'algorithme de dichotomie.
Activité proposée par Stéphane ROEBROECK
Vous avez un "bac à sable" à disposition pour vos essais.
- Une activité qui permet d'appréhender l'algorithme de dichotomie.
- Première phase
- Mettez-vous par deux et faîtes le jeu suivant : l’un des deux choisit un nombre entier au hasard entre 1 et 100, il le note quelque-part. L’autre doit retrouver le nombre. Pour cela, il fait des tentatives. A chaque tentative son ou sa camarade lui dit si c’est le bon nombre ou pas, et, si nécessaire, si le nombre proposé est trop grand ou trop petit. Notez le nombre de tentatives pour trouver le bon nombre.
- Refaire plusieurs fois le jeu et en changeant les rôles. Créer un tableau qui comptabilise le nombre de tentatives pour chaque parties.
- Imaginez que vous êtes seuls chez vous et vous souhaitiez rejouer. Vous allez écrire un programme pour remplacer celui du binôme qui choisit un nombre au hasard.
- Exécuter
from random import randintpuis faire plusieurs foisrandint(1,6)(remarque : la ligne doit toujours débuter par trois chevrons si vous êtes en mode console). Qu’obtenez-vous ? for i in range(10) : randint(1,6). Qu’obtenez-vous ?-
Qu’obtenez-vous ?c=1 while c<=10 : randint(1,6) c=c+1 - Entrez
5/2puis5//2Quelle différence observez-vous ? - Entrez
int(2.5)puisint(2.9)puisint(3.1)puisint(-2.2). A quoi sert la fonction int() ? - Ecrire ci-dessous un algorithme susceptible de remplacer le joueur qui cherche à faire deviner le nombre.
- Traduire cet algorithme en python, l’écrire dans l’éditeur d’edupython et le tester.
- Deuxième phase
- Reprenez le tableau des tentatives réalisées lors de la séances précédentes. Pour chacun des deux « chercheurs », calculez le nombre moyen de tentatives :
- Décrire la méthode que vous utilisez.
- Avec les autres binômes, discutez de la meilleure méthode à utiliser.
- Décrire la méthode dite "par dichotomie"
- Modifiez le programme écrit lors de la première séance pour faire jouer le programme contre lui-même.
- Ajouter les lignes nécessaires pour que le programme affiche à la fin de la recherche le nombre qu’il fallait trouver ainsi que le nombre de tentatives qui ont été nécessaires pour le retrouver. Vous réalisez ainsi la simulation de deux personnes qui jouent au jeu du « nombre à retrouver ». Faîtes tourner le programme plusieurs fois. Ce programme fait-il mieux que vous ?
- Pour ceux qui ont bien avancé : compléter de nouveau le programme pour qu’il effectue autant de simulations que l’on souhaite et qu’il fasse la moyenne du nombre de tentatives nécessaires à chaque partie pour trouver le nombre caché. Tester ce programme et noter les résultats dans un tableau qui indique le nombre de simulations et la moyenne du nombre de tentatives.
- Pour vous y aider nous allons tester quelques séquences dans la console (ou le "bac à sable")
Un aperçu des fichiers jupyter proposés en téléchargement.
Transformer une version procédurale en fonctionnelle
Voici une version procédurale de la recherche des racines d'un trinôme.
from math import *
print("Recherche des racines du trinôme ax²+bx+c=0")
print("Veuillez entrer a, b, c")
a=float(input("a= "))
b=float(input("b= "))
c=float(input("c= "))
delta=b**2-4*a*c
if delta>0 :
print("Il y a deux racines : ")
x1=(-b+sqrt(delta))/(2*a)
x2=(-b-sqrt(delta))/(2*a)
print("x1 = ",x1)
print("x2= ",x2)
else :
if delta==0 :
print("Il y a une racine :")
x3=-b/(2*a)
print(" La racine est : ",x3)
else :
print("Il n'y a pas de racine")
Le but est de transformer ce programme en un ensemble de fonctions.
Ensemble de fonctions : périmètre et aire
Le but de l'activité est de réaliser un ensemble de fonctions qui permet de calculer l'aire et le périmètre des figures de base.
L'activité en PDF ici.Voici un exemple réalisé par des élèves de seconde
# réalisé par des éléves de seconde
# -*- coding: utf-8 -*-
from math import *
from random import *
import matplotlib.pyplot as plt
import numpy as np
def perimetre_carre(c):
"Renvoie le périmètre d'un carré de côté c"
assert(c>=0)
return 4*c
def aire_carre(c):
"Renvoie l'air d'un carré de coté c"
return c*c
def peri_rect(l, L):
"Renvoie le périmètre d'un rectangle de longeur L, et largeur l"
return (l+2)+(L+2)
def aire_rect(l, L):
"Renvoie l'air d'un rectangle de longeur L, et largeur l"
return l * L
def aire_triangle(base, hauteur):
"Renvoie l'air d'un rectangle quelconque avec une base et une hauteur"
return (base * hauteur) / 2
def peri_tri_isocelle(h, b):
"Renvoie le périmètre d'un triangle isocelle avec h comme hauteur, et b comme base"
return b+2*( sqrt( h**2 + (b/2) ) )
def peri_tri_rectangle(h, b):
"Renvoie le périmètre d'un triangle rectangle avec h comme hauteur, et b comme base"
return h + b +(sqrt(h**2 + b**2))
def peri_tri_equilateral(b):
"Renvoie le périmètre d'un triangle équilatèral avec b comme base"
return b * 3
def peri_cercle(r):
"Renvoie le périmètre d'un cercle de rayon r"
return 2 * pi * r
def aire_cercle(r):
"Renvoie l'aire d'un cercle de rayon r"
return pi * r**2
def periFigure():
return peri_cercle(1)+ peri_cercle(1)
def aireFigure():
return (aire_cercle(1)*2)+aire_carre(2)
Ensemble de fonctions : La géométrie analytique (avec des réalisations d'élèves)
Le but est de construire un ensemble de fonctions de géométrie analytique afin de déterminer la nature de différentes quadrilatères.
L'activité en PDF ici.Différentes réalisations d'élèves.
from math import *
def milieu(xA,yA,xB,yB):
xI=(xB+xA)/2
yI=(yB+yA)/2
return(xI,yI)
def distance(xA,yA,xB,yB):
return sqrt((xB-xA)**2+(yA-yB)**2)
def parallélogramme(xA,yA,xB,yB,xC,yC,xD,yD):
return(milieu(xA,yA,xC,yC)==milieu(xB,yB,xD,yD))
def losange(xA,yA,xB,yB,xC,yC,xD,yD):
return(parallélogramme(xA,yA,xB,yB,xC,yC,xD,yD)== True and distance(xA,yA,xB,yB)==distance(xC,yC,xB,yB))
def rectangle(xA,yA,xB,yB,xC,yC,xD,yD):
return(parallélogramme(xA,yA,xB,yB,xC,yC,xD,yD)== True and distance(xA,yA,xC,yC)== distance(xB,yB,xD,yD))
def carré(xA,yA,xB,yB,xC,yC,xD,yD):
return(rectangle(xA,yA,xB,yB,xC,yC,xD,yD) and losange(xA,yA,xB,yB,xC,yC,xD,yD))
# Créé par GOBILLOTJ, le 10/01/2019 en Python 3.4
from math import*
def d(xa,ya,xb,yb):
"formule distance dans un repère orthonormé"
return sqrt((xb-xa)**2+(yb-ya)**2)
def m(xa,ya,xb,yb):
"formule millieu dans un repère orthonormé"
return (xa+xb)/2 ,(ya+yb)/2
def p(xa,ya,xb,yb,xc,yc,xd,yd):
"""renvoie true si les coordonées donné
forment un parallélogramme sinon renvoie false"""
if m(xa,ya,xc,yc)==m(xb,yb,xd,yd):
return True
else: return False
def l(xa,ya,xb,yb,xc,yc,xd,yd):
"""renvoie true si les coordonées donné
forment un losange sinon renvoie false"""
return p(xa,ya,xb,yb,xc,yc,xd,yd)==True and d(xa,ya,xb,yb)==d(xa,ya,xd,yd)
def r(xa,ya,xb,yb,xc,yc,xd,yd):
"""renvoie true si les coordonées donné
forment un rectangle sinon renvoie false"""
return p(xa,ya,xb,yb,xc,yc,xd,yd)==True and d(xa,ya,xc,yc)==d(xb,yb,xd,yd)
def c(xa,ya,xb,yb,xc,yc,xd,yd):
"""renvoie true si les coordonées donné
forment un carré sinon renvoie false"""
return r(xa,ya,xb,yb,xc,yc,xd,yd) and l(xa,ya,xb,yb,xc,yc,xd,yd)
représenter une fonction
Voici un ensemble de fonctions qui permet de traiter différentes formes de représentation graphique. A tester.
# coding: utf-8
'''
======================
Initiation à Matplotlib
Formation Python Académie de Reims 2019-2020
====================
'''
from math import *
from random import *
import matplotlib.pyplot as plt # importation classique du module matplotlib.pyplot sous l'alias plt
import numpy as np
# La première ligne permet d'éviter des soucis d'encodage
# Suit l'entête qui présente le programme
# Les quatre lignes suivantes importent des modules qui nous seront nécessaires.
# Par défaut, on gagnera à mettre ces lignes en début de chaque programme.
def f(x):
return x**2
def demo1():
"Affiche basique la courbe de la fonction f"
# A partir de deux listes, on peut créer un graphique.
# La première instruction crée le graphique et nous verrons que l'on peut ajouter des éléments supplémentaires à ce graphiqe.
# La seconde instruction affiche l'ensemble.
lx=np.linspace(-2,2,15) #crée une liste de 15 nombres allant de -2 à 2
# On peut créer une listes de valeurs en calculant les images de tous les éléments de lx en écrivant f(lx):
plt.plot(lx,f(lx))
plt.show()
def demo2():
"Affiche avec quelques options la courbe de la fonction f"
lx=np.arange(-4,6,0.01)
plt.title("demo2")
plt.plot(lx,f(lx),color='r')
plt.axis([-3,4,-1,17])
plt.axhline(color="b")
plt.axvline(color="g")
plt.show()
def demo3():
" Création d'un histogramme à pas inégaux"
plt.title("demo3")
lvaleurs=[2,5,5,5,7,8,8,9,9,9,10,10,12,13,13,15,17,18,19]
lbornes=[0,6,8,10,12,15,18,20]
plt.hist(lvaleurs,lbornes,normed=True)
plt.savefig("graphique.png") #que l'on peut-même enregistrer comme image
plt.show() #Affichage du graphique
def demo4():
"Affichage d 'un nuage de points aléatoires"
lx=np.random.uniform(0,1,1000)
ly=np.random.uniform(0,1,1000)
plt.title("demo4")
plt.scatter(lx,ly,color="r")
plt.axis([-0.2,1.2,-0.2,1.2])
plt.axhline(color="k")
plt.axvline(color="k")
plt.show()
def demo4b(nb=1000):
"Affichage d 'un nuage de points aléatoires et test de leurs présence dans un dique"
plt.title("demo4b")
plt.axhline(color="k")
plt.axvline(color="k")
disque=0
for i in range(nb):
x=uniform(-1,1) #Renvoie un nombre aléatoire de entre -1 et 1
y=uniform(-1,1)
R=sqrt(x**2+y**2)
if R<1:
plt.plot(x,y,"og")
disque=disque+1
else:
plt.plot (x,y,"or")
#plt.pause(0.01) #fonctionne mal sous Jupyter mais bien sous EduPython
print(disque/nb)
print(disque/nb)
plt.show()
# In[11]:
def g(x,a=1):
return 1/(x-a)
def demo5():
'Annotations dans un graphique en Latex et Axes du repère'
lx= np.linspace(-1,4,120)
plt.plot(lx,g(lx,2),'rx')
plt.title("demo5")
#Déplace les axes du repère
#Aller voir : https://python.developpez.com/tutoriels/graphique-2d/matplotlib/#LII-G
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
#xy=(1, 0) désigne la pointe de la flèche
#xytext=(-120, +30) désigne le décalage du texte par rapport à cette pointe
plt.annotate(r"$(\frac{1}{x-a})$ n'est pas définie en $a$",
xy=(2, 0), xycoords='data',
xytext=(-100, +30), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.show()
def demo6():
"afficher plusieurs sous-graphique dans un même graphique"
# En testant puis en copiant-collant le code ci-dessous, afficher les graphiques des fonctions composées nommées g,h,k et définies par (f(x)+2) ; (f(x+2)) et (-f(x)) en y ajoutant tous les commentaires nécessaires.
lx= np.linspace(-3, 3, 100) #rempli la liste lx de valeurs allant de -2 à 2
plt.subplot(221) #Pour s'occuper du graphique numéro dans un tableau de graphique 2×2
plt.subplots_adjust(hspace=0.4) #Pour espacer les graphiques
plt.title("Graphique 1 de la demo6")
plt.plot(lx,f(lx))
plt.subplot(222)
plt.title("Sous Graphique 2")
plt.plot(lx,f(lx))
plt.subplot(223)
plt.title("Sous Graphique 3")
plt.plot(lx,f(lx))
plt.subplot(224)
plt.title("Sous Graphique 4")
plt.plot(lx,f(lx))
plt.show()
def h(x):
if x<0:
return -x
else:
return x
def demo7():
"Le graphique d'une fonction qui n'est pas définie par une simple formule"
lx=np.arange(-4,6,0.5)
#ly=f(lx) cette commande ne peut alors pas fonctionner car on ne peut effectuer le test lx<0
# Il faut plutôt faire la méthode suivante pour forcer le calcul pour chaque élément de la liste
ly=[h(x) for x in lx] #la liste ly est crée à partir de chaque élément de la liste lx
plt.title("demo7")
plt.plot(lx,ly)
plt.show()
def demo8():
"Et pour aller plus loin"
"Tout est possible, le mieux est toujours de partir d'exemples et de les copier-coller pour se les approprier"
lx=np.linspace(-3,5,20) #Une liste de 20 nombres de -2 à 2
plt.title("La courbe de la fonction f demo8")
plt.plot(lx,f(lx))
plt.xlim(-3,5)
plt.ylim(-5,5)
plt.scatter(-1,f(-1))
plt.show()
def demo9():
"encore plus loin"
lx=np.linspace(-3,5,20) #Une liste de 20 nombres de -2 à 2
plt.title("La courbe de la fonction f demo9")
lx=np.linspace(-10,10,200)
plt.plot(lx,f(lx),"r--",label='Courbe de f') #Pour la couleur et la forme
lx2=np.linspace(-10,10,20) #seulement 20 points
plt.plot(lx2,f(lx2),"o", label='Images des entiers')
plt.grid(True) #Pour afficher une grille
plt.ylim(-2,20)
plt.legend(loc='upper right') #Pour afficher les label définis plus haut
plt.savefig('Courbe de f.png') #On peut même l'enregistrer dans un fichier image
plt.show()
def demo10(xmin=-10,xmax=+10,pas=0.001,lxp=[-6,-4,2,3],p_graduations_abs=1,p_graduations_ord=2):
"Affiche la courbe de f dans un repère quadrillé en parquant les points dont les abscisses sont dans lxp"
"et la graduation de la grille dans p_graduations_abs=1,p_graduations_ord=2"
lx=np.arange(xmin,xmax+pas,pas)
#ly=f(lx)
ly=[f(x) for x in lx]
ymin,ymax=min(min(ly),0),max(max(ly),0) #valeurs min et max de l'axe des ordonnées
plt.title("La courbe de la fonction f demo10")
plt.xlim(xmin,xmax) # valeurs min et max de l'axe des abscisses
plt.axis([xmin,xmax,ymin,ymax])
plt.yticks(range(int(ymin),int(ymax+1),p_graduations_ord)) # graduations des axes des ordonnées
plt.xticks(range(int(xmin),int(xmax+1),p_graduations_abs)) # graduations des axes des abscisses
plt.grid(True) #affiche un quadrillage
# plt.axis('equal')
# plt.title("fonction de la leçon")
axes = plt.gca()
axes.spines['right'].set_color('none')
axes.spines['top'].set_color('none')
axes.xaxis.set_ticks_position('bottom')
axes.spines['bottom'].set_position(('data',0))
axes.yaxis.set_ticks_position('left')
axes.spines['left'].set_position(('data',0))
plt.plot(lx,ly) # Affichage dela courbe de f
lyp=[f(x) for x in lxp] # Affichage des points supplémentaires
plt.scatter(lxp,lyp,c='red',marker='x')
plt.show() #Affichage du graphique
def demo():
demo1()
demo2()
demo3()
demo4()
demo4b(300)
demo5()
demo6()
demo7()
demo8()
demo9()
demo10(-4,4,lxp=[-1,0,1])
demo()
Une animation avec Python
Fluctuation des frèquences de succès. Animation tirée de l'espace Eduscol.
Ressources n°8
d'Eduscol
Créer et importer sa propre bibliothèque
Vous pouvez créer votre propre bibliothèque. Il faut enregistrer votre fichier au format .py . Il existe plusieurs méthodes. L'exemple proposé concerne un fichier de mathématiques appelé analytique.py qui possède des fonctions de géométrie analytique (distance, milieu, etc.).
Une partie du fichier analytique.py
from math import *
def milieu(xA,yA,xB,yB):
""" Renvoie les coordonnées du milieu du segment [AB]
pour appeler la fonction milieu, il faut écrire milieu(1,1,3,-1) pour A(1;1 et B(3;-1)"""
return (xA+xB)/2,(yA+yB)/2
# Ecrire la fonction distance(xA,yA,xB,yB) qui renvoie la distance AB
def distance(xA,yA,xB,yB):
""" Renvoie la distance AB
pour appeler la fonction distance, il faut écrire distance(1,1,3,-1) pour A(1;1) et B(3;-1)"""
d=sqrt((xB-xA)**2+(yB-yA)**2)
# x**2 correspond à x²
# sqrt(x) correspond à la racine carrée de x
return d
# méthode 1 : cette commande fonctionne si les deux fichiers sont dans le même dossier.
from analytique import *
# méthode 2 : cette commande fonctionne si le fichier est dans le sous-dossier module
from module.analytique import *
# Méthode 3 : créer votre module dans C:/EduPython/Lib/site-packages
from analytique import *
# Méthode 4 : plus compliquée
import sys
sys.path
sys.path.append("C:\\Users\\Pascal\\Google Drive\\Lycée général\\Python\\ModulesPersonnels") # Chemin à adapter à votre configuration
Exemple d'exécution
from analytique import *
distance(1,1,2,2)
help(distance)
La bibliothèque turtle
Activité proposée par Stéphane ROEBROECK
De jolis dessins :
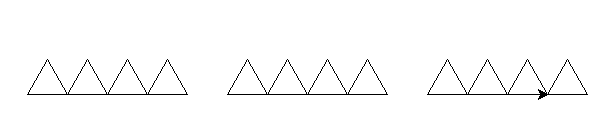
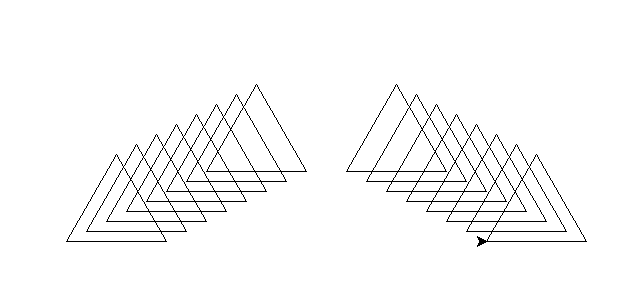
L'activité à télécharger : Téléchargement ici
Les solutions ici :
import turtle
turtle.speed('fast')
def triEqui(x,y,c):
"""trace un triangle équilatéral sur la gauche,
à partir du point de coordonnées (x;y) et de côté c (points)"""
turtle.up() #lève le stylo
turtle.goto(x,y) #se rend sur le point de coordonnées (x;y)
turtle.down() #descend le stylo
for i in range(3):
turtle.forward(c)
turtle.left(120)
for i in range(8):
triEqui(-200+20*i,-100+10*i,100)
for i in range(8,16):
triEqui(-80+20*i,50-10*i,100)
turtle.mainloop()
import turtle
turtle.speed('fast')
def triEqui(x,y,c):
"""trace un triangle équilatéral sur la gauche,
à partir du point de coordonnées (x;y) et de côté x (points)"""
turtle.up() #lève le stylo
turtle.goto(x,y) #se rend sur le point de coordonnées (x;y)
turtle.down() #descend le stylo
for i in range(3):
turtle.forward(c)
turtle.left(120)
def ligneTriangles(x,y,c,n):
"""Fait une ligne de n triangles à partir du point (x;y)."""
turtle.up() #lève le stylo
turtle.goto(x,y) #se rend sur le point de coordonnées (x;y)
turtle.down() #descend le stylo
for i in range(n):
triEqui(x,y,c)
x=x+c #augmente l'abscisse de c pour faire le triangle qui suit à côté du précédent
def ligneComplete(x,y,c):
for i in range(3):
ligneTriangles(x,y,c,4)
x=x+5*c
ligneComplete(-300,0,40)
turtle.mainloop()
Du Python débranché
Vous pouvez intégrer la pratique de python dans le cadre de vos rituels
Version embarquée :
Partie téléchargement
Quelques exemples d'activités mentales autour de Python (version pdf).
Quelques exemples d'activités mentales autour de Python (version docx).
Activité du type calcul mental avec différentes structures (version présentation)
Activité du type calcul mental avec instructions conditionnelles et fonctions (version présentation)
Ressources supplémentaires
Le parcours france IOI
Sur le site FranceIOI, vous avez la possibilité de créer un groupe et demander aux élèves de s'inscrire à ce parcours.
Vous pourrez visualiser l'avancée des élèves.
Site france IOIQuelques impressions écrans du site.


Des ressources eduscol
Il y a (pour l'instant) 13 ressources sur le site eduscol : accès direct
Vous pouvez lire ici le préambul de ces ressources :
Des vidéos
Quelques espaces vidéos
L'espace Lumni
Accès directPour vos réalisations
Vous pouvez nous adresser vos réalisations. Nous pouvons les proposer aux collègues dans cet espace.
- Johan MONTEILLET : variables et affectations en seconde
- Johan MONTEILLET : instructions conditionnelles en seconde
Un mémo Python
Téléchargement du mémo en version pdf.Téléchargement du mémo en version docx.
L'ensemble de ce site
Le squelette complet de ce site (disponible en fin de formation).
Enseignants formateurs en mathématiques de l'académie de Reims. Mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.